高考研题“四重境界”——以2022年新高考Ⅰ卷第15题为例

福建省福州高新区第一中学(闽侯三中) (350299) 洪雪金

1．真题呈现

(2022年数学新高考Ⅰ卷·15)若曲线y=(x+a)ex有两条过坐标原点的切线，则a的取值范围是．

2．第一重境界：通技通法，守住“底线”

根据题目条件的分析与理解，结合条件确定切线方程，为进一步的求解提供条件，从而确定数学问题求解的“通技通法”，也是数学教学与学习的初级境界——第一重境界，守住“底线”．

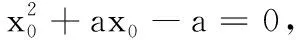
评注：本解法中切线方程的确定，很好综合了导数的运算与几何意义、直线的方程等相关知识，又联系函数与方程、不等式等相关知识，具有很好的知识交汇性与融合性．

3．第二重境界：巧技妙解，发散思维

探索数学问题的实质，探寻“巧技妙解”，利用导数的几何意义与直线的斜率公式，从不同的层面来确定直线的斜率，形成两者的一致性，这是数学教学与学习的第二重境界，充分发散数学思维．

评注：本解法关键是构建两斜率相等的关系式，从而转化为对应的方程问题，再利用方程的判别式与不等式的求解来确定参数的取值范围．切线方程斜率的不同求法，为问题的解决提供了广阔的思路．

4．第三重境界：追根溯源，合理归类

深挖问题的内涵，合理追根溯源，回忆并联系教材实例或高考真题，形成知识的反馈，构建知识体系，这是数学教学与学习的第三重境界，合理归类，脱离“题海”，“促双减”，提效益．在2021年的新高考试卷中也有该问题的“影子”，如利用过“动点”到“定曲线”的切线有两条来确定参数的大小关系问题．

例1 (2021年数学新高考Ⅰ卷·7)若过点(a，b)可以作曲线y=ex的两条切线，则( ).

A．eb

C．0

解析：由于函数y=ex是定义域R上的增函数，导函数y′=ex>0恒成立，设切点为(t，et)，则切线方程为y=et(x-t)+et，则有b=et(a-t)+et，整理可得(t-a-1)et+b=0，构造函数f(t)=(t-a-1)et+b，求导可得f′(t)=(t-a)et，由f′(t)=0解得t=a，则当t∈(-∞，a)时函数f(t)单调递减，当t∈(a，+∞)时函数f(t)单调递增，根据题意可知，方程f(t)=0有两解，所以f(t)min=f(a)=-ea+b<0，即b0，此时存在x2∈(-∞，a)，使得f(x2)=0.综上，可得0

评注：该高考真题改变视角，从另一个层面来阐述过“定点”到“动曲线”的切线有两条来确定参数的取值范围问题．

5．第四重境界：思变笃行，举一反三

在掌握对应数学问题的“通技通法”与“巧技妙解”，以及“追根溯源”的基础上，探寻对应数学问题的变式，倡导“思变笃行”，这是我们数学教学与学习的第四重境界，有效举一反三．

探究1 根据高考真题以及相应的解析过程，改变过坐标原点的切线的条数，可以得到以下两个相应的变式问题．

变式1 若曲线y=(x+a)ex有且只有一条过坐标原点的切线，则a的取值范围是．(答案：{-4，0}．)

变式2 若曲线y=(x+a)ex没有过坐标原点的切线，则a的取值范围是．(答案：(-4，0)．)

评注：上述变式是在原高考真题的解析基础上加以拓展的，通过这种探究，更有效地巩固了相关的知识点、思想方法及能力要求.

探究2 根据高考真题的情境创设，合理改变条件与题型，引入动点与切线的变数情况，得到以下对应的变式问题．

变式3 若过点P(1，λ)最多可作出n(n∈N*)条直线与函数f(x)=(x-1)ex的图象相切，则下列结论中错误的是( ).

A．λ+n<3

B．当n=2时，λ的值不唯一

C．λn可能等于-4

图1

评注：本题以“动点”与“定曲线”的位置关系，增加了“变”的切线数，使得问题更加复杂，求解中抓住了问题的本质，结合导数的运算与几何意义，并综合利用函数的单调性，构建知识之间的交汇与融合，从而形成知识网络与应用体系．

综上可见，在具体的数学教学及解题研究过程中，借助实际数学解题研究的“四重境界”——通技通法，巧技妙法，追根溯源，思变笃行，从“通技通法”到“巧技妙法”，是“底线”的突破与思维的发散；从“巧技妙法”到“追根溯源”，是思维与方法的提升；从“追根溯源”到“思变笃行”，是知识积累到能力升华的飞跃．数学解题研究的“四重境界”，逐步递进，螺旋上升，在一定程度上可以发散并拓展学习者的数学思维，真正实现提升数学品质，提高数学能力，培养数学核心素养的目标．