双液压马达驱动沉桩系统的自同步理论
2022-11-08赵春雨端维海姜孟超王元昊
赵春雨,端维海,姜孟超,王元昊
(东北大学 机械工程与自动化学院,辽宁 沈阳 110819)
目前打桩机已广泛应用于工程实际中,其产品种类繁多,适用范围也较为不同.如螺旋式打桩机,桩机通过动力头带动钻杆钻头向下钻孔,成孔漂亮、清底干净,但只能打硬土,不适用于淤泥、黏土以及流沙等场所.柴油锤打桩机利用桩锤往复跳动的冲击力和桩体本身的重力来克服土层的阻力,进而实现沉桩;该桩机结构简单,在软土条件下,柴油锤在运行过程会出现失速现象,并且噪声较大,不适合城市打桩[1].液压静力压桩机使用高压油产生强大的静压力,将桩基逐步压入地下,工作平稳且噪声较小,但是该桩机体积过大,不便移动和小场所沉桩[2].振动沉桩机通过振动器产生激振力,使预制桩产生高频振动,桩体与周围土壤之间摩擦力以及桩端阻力减小,桩体在其与桩机自重作用下下沉,最终实现沉桩.振动沉桩机构造简单、使用方便、效能高、附属机设备少、噪声较小,符合城市打桩要求.
自第一台BT-5型振动沉桩机研发成功以来[3],振动沉桩机吸引了国内外学者的关注.Bingham等[4]设计出双电机驱动两对齿轮同步偏心转子的振动沉桩机,并提出了桩与土壤接触参数的识别方法和依据土壤接触参数控制桩机振幅和频率的方法.但振动电机驱动能力有限,很难在大负荷下实现稳定控制,由于桩机采用齿轮刚性传动方式,系统无法实现自同步运行,齿轮传动系统也会因负载变化受到较大冲击力,造成齿轮损坏,降低桩机使用寿命.闻邦椿等[5]提出了研究多液压马达驱动的同步问题.Luo等[6]设计出双液压马达驱动偏心转子系统,分析了两液压马达结构、油温和阻尼系数等微小差异对耦合运动的影响,得到了同步运动的判据并提出了提高振动同步稳定性的相应措施.尽管振动沉桩机已经在系统与结构上取得了较大优化,但大部分沉桩系统仍处于亚共振状态,并未涉及远超共振等相关研究.在惯性振动筛的设计研究中,筛机工作状态处于远超共振状态,其工作频率远大于系统的固有频率,而在亚共振状态下,筛机无法妥善地消振,故亚共振状态很少采用[7].因此,有关不同共振系统在同一个振动机械上的应用问题仍有待解决.
本文提出了一种能够产生远超共振和亚共振两种状态的双液压马达驱动沉桩振动系统,并建立了该系统的动力学模型,推导出两种工况下系统的同步稳定性判据及其动力学参数范围,最终通过C语言程序对振动沉桩过程进行了计算机仿真.相较于其他双机振动系统,该系统拥有两种共振状态,当桩机处于待机状态时,振动系统处于远超共振状态,两偏心转子以π相位差同步运行,激振力相互抵消;当桩机处于沉桩状态时,振动系统处于亚共振状态,两偏心转子以0相位差同步运行,激振力相互叠加.
1 振动系统机构及工作原理
图1a为新型双液压马达驱动自同步振动沉桩机的结构示意图.桩机由起吊横梁1、机箱2、横梁筋板3、剪切橡胶弹簧4、金属板5、夹桩器6、电液传动系统7(电动机、液压泵和液压马达串联组成)、旋转轴8、偏心转子9以及套轴10等部分构成.两根旋转轴通过滚子轴承对称安装于机箱内部左右两侧,并与安装在机箱外部的液压马达相连接.每个偏心转子对称安装在旋转轴上,通过液压马达带动旋转轴,实现转子的转动.机箱通过套轴分别与横梁筋板和金属板连接,套轴与横梁筋板和金属板之间的轴孔采用间隙配合,同时为了限制激振器横向位移,套轴的轴肩只与金属板内侧相接触且不与横梁筋板接触.如图1b所示,起吊横梁和金属板通过剪切橡胶弹簧连接.而其工作状态分为待机和打桩两种状态,如图2所示.

1—起吊横梁;2—机箱;3—横梁筋板;4—剪切橡胶弹簧;5—金属板;6—夹桩器;7—电液传动系统;8—旋转轴;9—偏心转子;10—套轴.
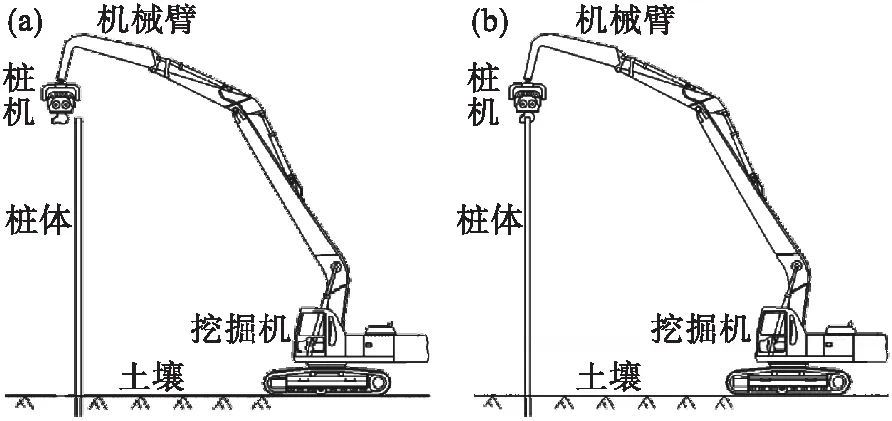
图2 沉桩机工作状态示意图
2 系统动力学模型
2.1 电机-泵-马达动力传动系统的驱动力矩
液压传动具有传动平稳、调速方便、功率体积较大等特点,其广泛应用于各种领域[8],本文选用如图3所示的双液压马达驱动振动沉桩机液压传动系统,能量传递过程如图4所示.

1—异步电动机;2—液压泵;3—溢流阀;4—过滤器;5—单向阀;6—电磁换向阀;7—双向定量液压马达;8—冷却器.

图4 振动沉桩机系统能量传递过程[9]
设液压马达容积效率为ηmv,理论流量为Qmt,转速为nm,故液压马达的实际输入流量Qm为
(1)
式中:角速度ωm=nmπ/30;排量Vm=60Qmt/nm.
忽略管路损失,则液压泵的实际输出流量Qb等于马达实际输入流量Qm,即Qb=Qm,则液压泵角速度ωb为
(2)
式中:ηbv为液压泵的容积效率;Vb为液压泵的排量;Qbt为液压泵的理论流量,Qbt=Qb/ηbv;nb为液压泵的转速,nb=60Qbt/Vb.
电机角速度ωe等于液压泵的角速度ωb,即
由于液压泵的进油口和液压马达的出油口直接与油箱相连,故液压马达进、出油液压力差Δp等于液压泵输出口的油压pp,即Δp=pp.设液压泵机械效率为ηbm,所需驱动转矩为Tb,则
(3)
稳态运行时,则
(4)
式中,fe为电机转轴阻尼系数.
根据文献[9]得出稳态运行时电机的转矩:
(5)
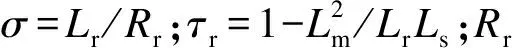
将式(4)代入式(3),得
(6)
由式(6)得出稳态运行时,液压马达理论输出力矩为
(7)

若系统稳态运行时液压马达在其角速度为ωm0附近存在微小波动,设波动系数为ν,即
ωm=(1+ν)ωm0.
(8)
将式(8)代入式(7),将其在ωm0附近泰勒展开,略去ν二次以上高阶项,得
Tm=Tm0-km0ν.
(9)
其中:Tm0为液压马达角速度为ωm0时的输出力矩;km0为液压马达角速度为ωm0时的速度刚度系数.
2.2 振动系统运动微分方程
图1所示的剪切橡胶弹簧,其法向刚度远大于其剪切刚度,通常两者比值大于30,所以认为液压马达驱动机构沿起吊横梁内壁仅在垂直方向运动,其动力学模型如图5所示.图中有两组弹簧阻尼器,kz1和fz1,kz2和fz2.当系统处于打桩状态时,如图2b所示,夹桩器与桩夹紧,支撑在土壤中,kz1和fz1为土壤的刚度和阻尼;此时,套轴10上表面压紧在横梁筋板3上,kz2和fz2为横梁筋板3在垂直方向的刚度和阻尼.当系统处于待机状态时,如图2a所示,夹桩器与桩脱离,桩锤被吊起,套轴10下表面通过金属板5与橡胶剪切弹簧4相连,此时kz2和fz2橡胶剪切弹簧在垂直方向的刚度和阻尼,而kz1和fz1为0.

图5 振动系统的动力学模型
振动系统的运动微分方程:
(10)
式中:i=1,2;m0是两偏心转子的质量;M=m+2m0+mc,m是激振器质量,而mc待机状态为0,沉桩状态为桩的质量;r是两偏心转子的半径;kz=kz1+kz2;fz=fz1+fz2;Ji,fi分别为液压马达i转动惯量和阻尼系数;Tmi是液压马达i输出力矩.
3 两偏心转子的同步条件
3.1 两偏心转子的无量纲耦合方程
设当系统稳态运行时偏心转子的平均相位角为α,偏心转子1超前于φ为α,偏心转子2落后于φ为α,即φ=φ1-α=φ2+α[9].
由于系统运动是周期性变化,因而马达转速以相同周期变化.设稳态运行时两偏心转子的周期为T1和T2,取两偏心转子的最小公倍周期T0,则
(11)
若设瞬时平均转速和相位差波动系数分别为ε1和ε2,即
(12)
由于稳态时液压马达转速变化较小,故可忽略角速度对激励的影响,则式(10)中第一个方程可简化为

(1+ν2)2sin(φ-α)].
(13)
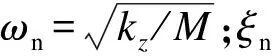
由式(13)得出系统运动微分方程的稳态相应解:
z=rzrμ[sin(φ+α-γ)+sin(φ-α-γ)].
(14)
式中:

(15)
式中:
Wc=rzμcosγ;Ws=rzμsinγ.
将式(9)代入式(15),整理成矩阵形式:
(16)
式中:
3.2 双液压马达自同步运行条件

(17)
将式(17)中的两式相减,整理可得
(18)
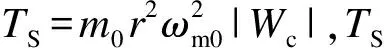

TS≥|TD|.
(19)
由此可见,当两马达的同步力矩大于或等于其输出转矩差的绝对值时,两偏心转子实现同步运行.
3.3 双液压马达自同步稳定性条件
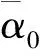
(20)
式中:
c31=0,c32=0,c33=1;
假设C=E-1D求出矩阵C,进而通过det(C-λI)=0得出矩阵C的特征方程:
λ3+c1λ2+c2λ+c3=0.
(21)
式中:
由Routh-Hurwitz准则可知,当且仅当式(21)中λ的解均为负实部,同时矩阵C的特征方程(21)中的参数满足
c1>0,c3>0,c1c2>c3
(22)
时,式(20)的解e=0是稳定的.由于H0>0,因而双液压马达同步运行的稳定性条件为
H0>0,H1>0,H3>0,H4=4H1H2-H0H3>0.
将上述公式整理可得
(23)
4 系统同步状态数值分析
初步选定系统性能参数,两偏心转子质量为m0=20 kg,半径大小为r=0.2 m,旋转中心距离l0=1 m.激振器质量为1 200 kg.电动机选取型号相同的三相异步电动机(380 V,50 Hz,6-极,Δ-连接,额定功率4 kW,额定转速960 r/min),电机中定子电阻Rs=0.56 Ω,转子电阻Rr=0.54 Ω,定子电感Ls=0.075 H,转子电感Lr=0.075 H,互感Lm=0.074 H,fei=0.01.选取型号相同的液压泵(排量Vb=40 cm3/r,容积效率ηmv=0.95,机械效率ηbv=0.95),以及型号相同的液压马达(排量Vb=40 cm3/r,容积效率ηmv=0.95,fi=0.01).
将各装置的参数值代入式(7)和式(9)中,计算得
(24)
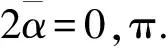
4.1 待机状态下系统的数值分析
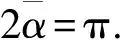

图6 待机状态下的稳定性指标随参数rz的变化(n=4)
4.2 沉桩状态下系统的数值分析

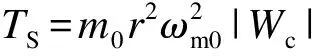
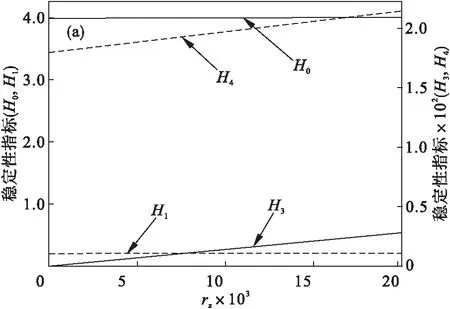
图7 沉桩状态下的稳定性指标随参数rz的变化(n=0.4)
5 系统仿真分析
5.1 待机状态下系统的仿真分析
当桩机处于待机状态时,套轴10下表面与金属板5接触,系统处于远超共振状态.通过C语言编程对振动系统进行仿真分析,图8为计算机仿真结果.由图可知:系统启动后,双液压马达转速从0逐渐增大,在2.1 s后进入同步运行状态,转速达到998.98 r/min,转子的稳态相位差为179.98°.桩机在z方向上的振幅随时间逐渐衰减,最终在3.5 s后振幅开始逐渐稳定于0,系统处于静止状态.
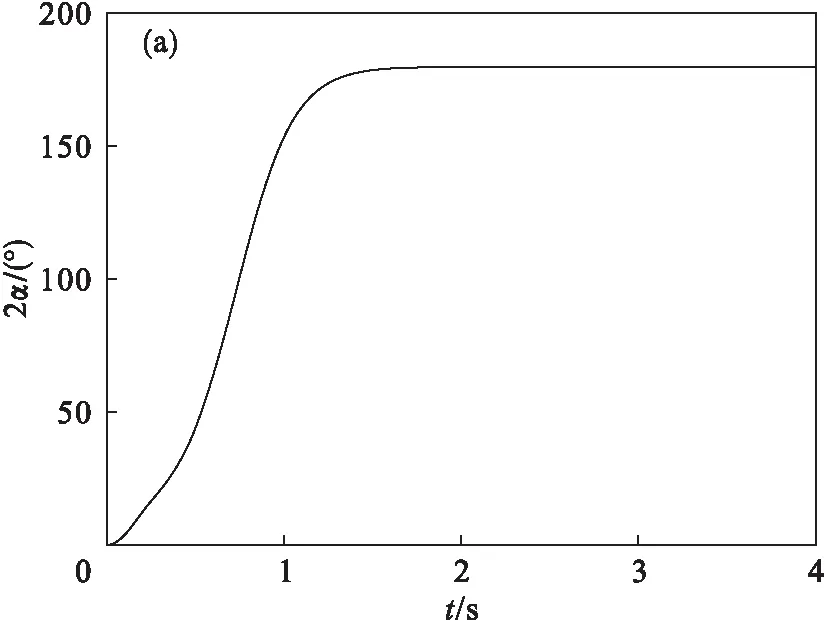
图8 待机状态下数值仿真结果
5.2 沉桩状态下系统的仿真分析
当桩机开始沉桩时,套轴10上表面与横梁筋板3接触,振动系统的刚度和阻尼发生改变,系统由远超共振状态转变为亚共振状态.通过C语言编程对系统进行仿真分析,图9为沉桩状态下计算机仿真结果.由图可知:沉桩初期,双液压马达转速发生改变,系统在z方向上的位移发生波动.在0.6 s时,双液压马达再次进入同步运行状态,转速稳定于998.98 r/min,稳态相位差为1.2°,系统在z方向上的位移激励振幅稳定于1.4 mm.故桩机在满足沉桩要求的同时其上下往复波动较小,产生的噪声小,一定程度上延长了桩机的使用寿命.
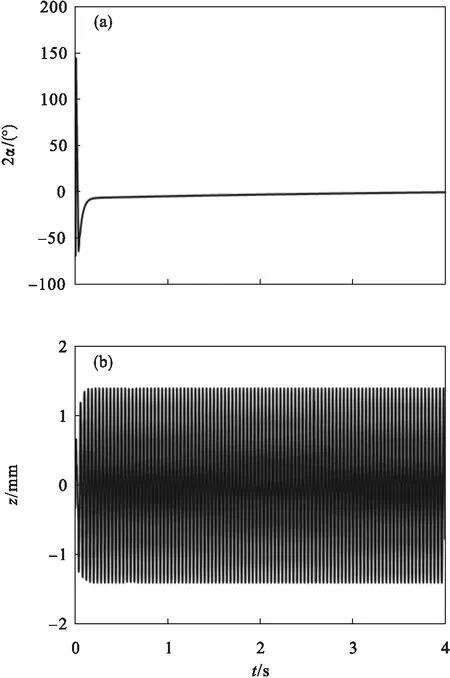
图9 沉桩状态下数值仿真结果
6 结 论
1)本文提出了新型双液压马达驱动自同步振动沉桩机,利用刚度变化使系统处于两种工作状态:当桩机处于待机状态时,振动系统处于远超共振状态,广义动态对称角为π,激振力相互抵消;当桩机处于沉桩状态时,振动系统处于亚共振状态,广义动态对称角为0,激振力相互叠加.
2)推导出偏心转子的无量纲耦合方程,得出了转子同步运行的条件及同步稳定性条件.数值计算结果表明:桩机在待机和沉桩两种不同状态下,系统均满足同步稳定性要求.
3)通过计算机仿真表明:待机状态时,两个偏心转子的稳态相位差为179.98°;沉桩状态时,两个偏心转子的稳态相位差为1.2°,系统处于亚共振状态,满足桩机的工作需求,实现了桩机的沉桩目的.
