基于SWU算法的西北多山地区GSM-R无线传播模型研究
2022-11-08闫光辉严天峰王逸轩周文颖
高 锐,闫光辉,严天峰,王逸轩,孙 禹,周文颖
(1.兰州交通大学 电子与信息工程学院,甘肃 兰州 730070;2.兰州交通大学 光电技术与智能控制教育部重点实验室,甘肃 兰州 730070;3.中国铁路兰州局集团有限公司 兰州通信段,甘肃 兰州 730050)
铁路数字移动通信系统(Global System of Mobile for Railway,GSM-R)是为保障我国铁路列车行车调度指挥通信,有效支撑铁路系统安全运营而专门设计、开发的数字移动通信系统[1]。出于对铁路行车的安全考虑,列车通信系统必须具备高可靠性、高有效性、高安全性和高可维护性[2-3]。这就对GSM-R系统提出了非常高的要求,在整个系统的开发过程中,无线信号的覆盖预测和网络规划成为提升GSM-R技术的关键和难点。因此,开展复杂环境下无线电波传播模型的研究,实现“基站—列车”链路间无线信号的精确覆盖预测,对提升我国铁路通信质量,促进铁路健康运营和可持续发展具有重要意义。
常见的电波传播模型可分为理论模型和经验模型两类。理论模型以电磁波传播理论为基础,主要方法有射线跟踪方法[4]、数值法[5]等。目前,理论模型研究中主要存在大尺度区域远场边界条件难以确定、模型参数过多、计算效率低等缺点,且需要大量的环境特征数据对周边建筑进行精确的三维建模,而现有条件往往难以实现。经验模型基于大量应用场景测试,通过统计分析找出反应其传播特征的参数特性,并建立传播模型,因其计算简单、便于实现,在工程中得到广泛应用。国内外比较著名的经验模型有Egli模型[6]、Okumura模型[7]、Okumura-Hata模型[8]、COST231-Hata模型[9]、ITU-R.P系列模型[10]和Lee模型[11]等。其中Lee[6]提出的Lee模型是一种基于地形数据,仅需开展少量测试即可进行场强预测的建模方式的大尺度宏蜂窝场景,被认为是最有效和准确的大尺度区域宏蜂窝模型之一。Lee模型包括“点—区域”和“点—点”两种模式。其中,“点—区域”模式通过对测试数据进行统计、参数估计等方式进行预测,适用于地形地貌数据不足的场景,具有场景通用性强、工程测试方便、准确度较高等优点。文献[12]比较了Okumura-Hata模型和Lee模型“点—区域”模式在移动无线信号覆盖场景下的预测准确度,认为其在国内应用更具有通用性,可作为场强预测的重要依据;文献[13]分析了多种校正方法,认为Lee模型“点—区域”模式经过校正后能够很好地应用于市区、郊区、开放空间和水上等多种场景。Lee模型“点—点”模式通过几何光学和绕射原理对特定地形下的路径损耗进行有效计算并做出预测,适用于地形地貌数据比较详尽,能够有效获取预测范围内任意“点—点”之间链路地形数据的场景。相比于“点—区域”模式,Lee模型的“点—点”模式可利用地形轮廓数据和光学理论对发射天线的有效高度增益进行精确计算,并通过Fresnel-Kirchoff衍射理论和Epstein-Petersen方法对复杂山区地形衍射损耗进行有效计算,以及通过频率补偿算法和模型参数校正因子对实际预测场景进行修正,大大提升预测精度。然而,“点—点”模式依赖于高分辨率数字高程模型(Digital Elevation Model,DEM)数据,需要将“点—点”链路经纬度信息与DEM数据进行一一映射,现有技术手段比较欠缺,开发实现难度大。此外,在工程应用中Lee模型“点—点”模式采用Epstein-Peterson方法存在以下问题:① Epstein-Peterson方法计算值要差于实际测量值;② 当障碍物近似于“发射端天线—接收端天线”的齐平时,Epstein-Peterson方法会产生非常大的误差,总衍射损耗约等于n倍单刃峰损耗(n为刃峰个数)[14];③ 当障碍物间隔较近或者传播余隙在介于0.6~1个第一菲涅尔区间时,Epstein-Peterson方法会引起刃形损耗计算值偏高[15-16];④ 在地形条件较为复杂的情况下,Epstein-Peterson方法需要对链路上所有刃峰进行识别并进行大量迭代计算,导致算法运行时间过长[17]。
本文基于DEM数据首选对覆盖区域进行了栅格化处理,实现对矢量经纬度位置信息与高程数据的一一映射,然后利用反距离权重插值算法(Inverse Distance Weighted,IDW)进行插值计算从而得到“点—点”链路有效高程数据。在此基础上,提出一种SWU衍射改进算法,对Lee模型“点—点”模式下衍射损耗预测精度有了显著提升;最后,利用Leaflet.js、HTML5、Vue3.js等WebGIS技术,实现对复杂环境下铁路无线信号覆盖的可视化仿真。
1 Lee大尺度区域模型
GSM-R属于特高频(Ultra High Frequency,UHF)频段,该频段受云、雨和雾等自然现象能量吸收较小,建模过程只需重点考虑电波传播中受地球的曲率、地形和建筑物引起的散射和绕射影响。因其电波传播特性,Lee模型非常适用于GSM-R业务场景。
1.1 Lee模型“点—区域”模式下接收信号场强Pr计算方法
Lee模型 “点—区域”模式提供了包括自由空间、开阔地区、森林或公园等自然场景和乡村、郊区、中小城市、典型大城市等不同规模人为建筑环境场景下的路径损耗对数曲线公式[18],可在无法开展测试的情况下使用相似场景模型对接收信号场强Pr0和路径损耗斜率γ参数进行预测。此外,还可开展少量测试来确定本地场景下的Pr0和γ,得到适用于本地的电波传播模型,通用计算式为
( 1 )
式中:r为发射站与接收站间距离;r0为发射站与接收站间距离1.609 km参考位置;Pr、Pr0分别为接收站在距离发射站r、r0处的接收信号场强;γ为路径损耗斜率;f0为参考频率校准基准,取850 MHz;n0为路径损耗系数,由实测频率f、参考校准频率f0和场景类型3个参数共同决定;α为模型校正因子。
由于实际场景往往与标准参数值存在出入,可通过式( 2 )计算模型校正因子α,微调实验参数值与标准参数值进行模型校正,提高模型预测精度。
α=α1+α2+α3+α4+α5
( 2 )
式中:α为模型校正因子;α1为功率校正因子;α2为发射天线高度校正因子;α3为发射天线增益校正因子;α4为接收天线高度校正因子;α5为接收天线增益校正因子。
根据Fresnel-Kirchoff衍射理论,在发射站到接收站的直射路径中有1个或多个刃型障碍物而受到阻挡,且传播余隙hp小于0.6个第一菲涅尔区间时,称之为有障碍物非视距(Non-Line of Sight,N-LoS)传播场景;而当不存在障碍物遮挡或障碍物遮挡产生的传播余隙hp大于或等于0.6个第一菲涅尔区间时,称为无障碍物视距(Line of Sight,LoS)传播场景。根据地形环境影响和铁路周边实际情况,将Lee模型的“点—区域”模式分为无障碍物视距传播场景和有障碍物非视距传播场景这两种场景。
(1)无障碍物视距(LoS)传播场景
在不同城市的大量测试表明,虽然测试数据的标准偏差含有地形影响,但通过平均化处理所得到的损耗曲线已经消除了地形变化带来的影响,并将其转化为平坦地形下人为建筑的路径损耗影响[19]。因此,在无障碍物视距(LoS)场景下,可通过少量测试来确定本地接收信号场强Pr0和路径损耗斜率γ,按式( 1 )计算得到接收站的信号场强Pr。
(2)障碍物非视距(N-LoS)传播场景
该场景下电波传播过程中会产生衍射损耗,计算Pr时,需在式( 2 )的基础上加上衍射损耗分量,即
( 3 )
式中:L(ν)为衍射损耗分量。
1.2 Lee模型“点—点”模式下衍射损耗计算方法
Lee模型“点—区域”模式中的衍射损耗分量L(ν)常根据工程人员经验设定,为固定参数值,但对于西北多山的场景,这种设定会带来较大衍射损耗误差,严重影响预测精度,因此引入“点—点”模式来解决多山地形造成的衍射损耗误差。
在“点—点”链路下障碍物非视距传播场景中,电波直射路径受到人为建筑以及自然环境影响且随着地形轮廓的不同变化产生增益或损耗。此时,为了对多山场景下铁路信号的覆盖范围进行精确预测,需要对衍射有效损耗Leff(ν)进行建模,如下
Leff(ν)=max[L(νk),Ltotal]
( 4 )
其中,
( 5 )
( 6 )
( 7 )
式中:hp为“点—点”链路与障碍物间的传播余隙;d1和d2分别为障碍物与发射站、与接收站之间的距离;ν为衍射因子;n为发射站与接收站之间障碍物总数;k∈[1,n],为发射站与接收站之间第k个障碍物;L(νk)为发射站与接收站之间第k个障碍物的衍射损耗;Ltotal为发射站与接收站之间障碍物衍射损耗总量;Leff(ν)为衍射有效总损耗。
在计算地形衍射影响时,须考虑电波与地形障碍物间的关系,分为无障碍物视距传播、单刃峰障碍产生衍射和刃峰障碍产生衍射三种情况。
(1)当电波传播过程中没有地形阻碍时,发射站与接收站间电波传播见图1。首先,根据“点—点”链路高程数据判断链路中任意位置点的hp是否都小于0.6个第一菲涅尔区间。若所有位置点的hp均满足此条件,则认为电波不受地形障碍影响,按照1.1节的方法进行计算。
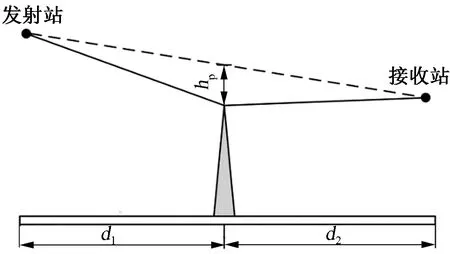
图1 电波视距LoS传播示意
(2)当电波传播过程中仅受孤立的单刃峰障碍影响时,发射站与接收站间电波传播见图2。此时,采用Anderson方法进行计算衍射损耗分量L(ν),先通过式( 5 )计算衍射因子v,再利用式( 6 )计算得到L(ν)。

图2 电波单刃峰传播示意
(3)当电波传播过程中受到多个刃峰障碍影响时,发射站与接收站间电波传播见图3。此时,采用Epstein-Peterson算法计算多刃衍射有效损耗Leff(ν),先按照单刃衍射情况计算得到所有刃峰的衍射损耗分量,再根据式( 7 )将所有刃峰的单刃衍射损耗分量相加得到衍射损耗总量Ltotal,最后根据式( 4 )获取所有刃峰的单刃衍射损耗分量与衍射损耗总量Ltotal中的最大值,即为多刃衍射有效损耗Leff(ν)。

图3 电波双刃峰传播示意
2 Lee模型“点—点”模式下的SWU衍射改进算法
在Lee模型“点—点”模式下,发射站与接收站之间的精确高程数据成为计算衍射损耗分量L(ν)的关键。本节通过IDW空间栅格插值转化算法从DEM数据中计算得到“点—点”链路高程数据。之后,在“点—点”链路高程数据基础上,提出了一种基于滑动窗口合并 (Sliding Window Union,SWU) 的衍射改进算法。
2.1 基于IDW空间的栅格插值转化算法
IDW算法是一种对非规则空间分布的高效内插算法,其算法思想是:离估值点距离越近的点对估值点影响越大,越远的离散点对估值点影响越小,甚至不产生影响。考虑到IDW算法计算简单、易于编程实现,适合于反应数据空间局部变化等优点,提出了一种基于IDW的栅格空间插值转换算法,先对矢量数据进行空间栅格化,之后利用IDW算法实现对“点—点”链路高程数据插值计算。
2.1.1 矢量数据的空间栅格化
对矢量数据进行空间栅格化表示见图4,图4中,(Blon,Blat)为覆盖区域左上角边界经纬度值;Δx为经度方向上栅格的最小间隔;Δy为纬度方向上栅格的最小间隔;黑点Pj为空间栅格三维坐标系(x,y,z)中一点;z为高程。
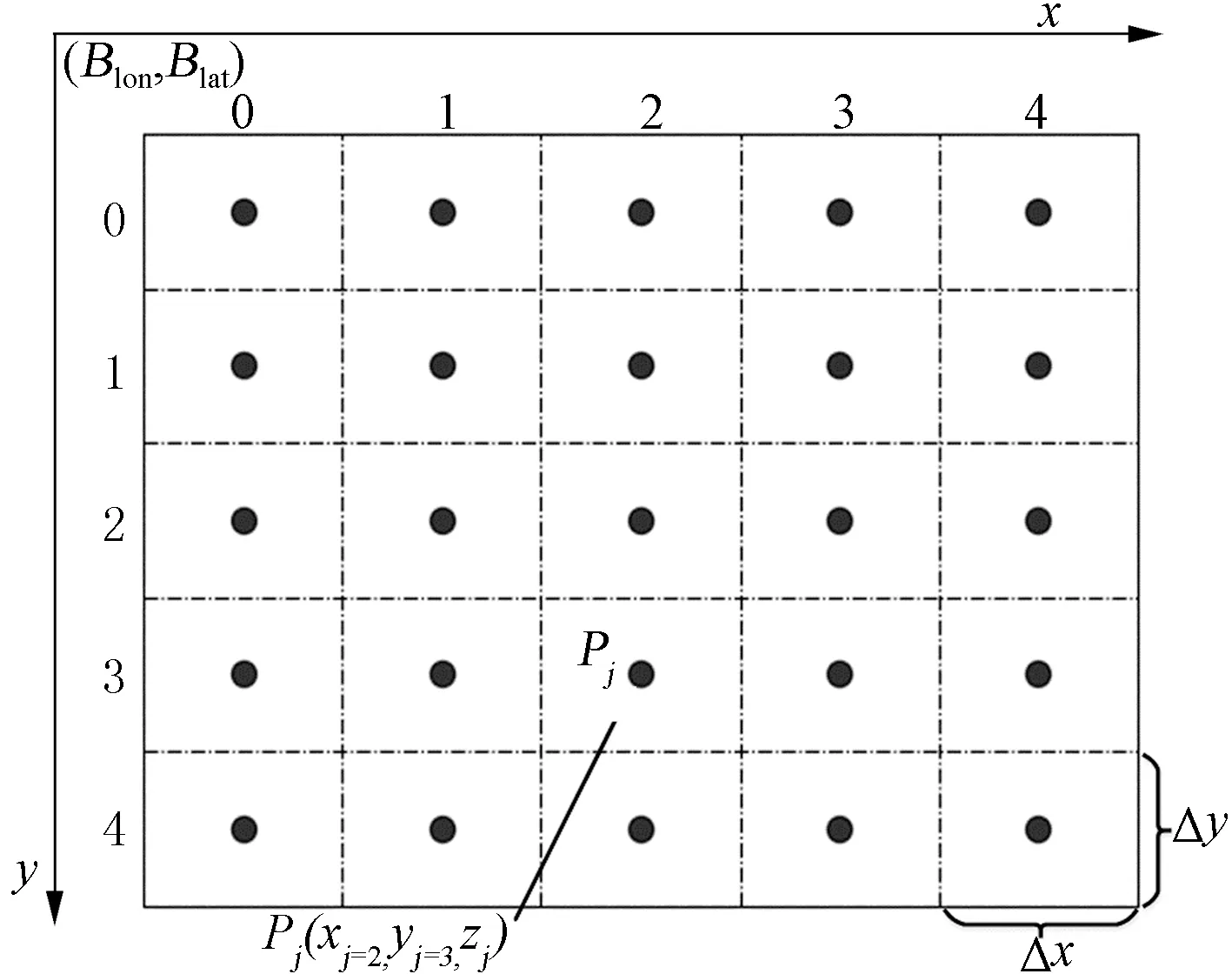
图4 矢量数据空间栅格化处理
矢量数据空间栅格化算法思路:首先,根据发射点经纬度(Slon,Slat)来设定覆盖区域范围d×d(d为覆盖区域直径,d=2,3,…,10);之后,依据覆盖区域范围,确定空间栅格化经度最小间隔Δx和纬度最小间隔Δy,以及覆盖区域左上角边界经纬度值(Blon,Blat) ;然后,利用开源栅格空间数据转换库(Geospatial Data Abstraction Library,GDAL)的Python API方法,从ASTGTM2 DEM数据集中获取经纬度坐标对应的高程z;最终,利用式( 8 )对不同分辨率的高程数据进行栅格化,使当前位置经纬度坐标(Clon,Clat)与空间坐标(x,y)一一对应,映射得到具有栅格位置和高程的三维数据集(x,y,z)。
( 8 )
2.1.2 IDW算法下的高程计算
IDW算法实现对“点—点”链路高程数据插值计算见图5。图5中,Tx为发射站坐标点;Rx为接收站坐标点;白点为“Tx—Rx”链路间的等间隔距离坐标点;Pi为“Tx—Rx”链路中的1点;P1、P2、P3和P4分别为空间栅格坐标系中距Pi距离最近的4个栅格点。
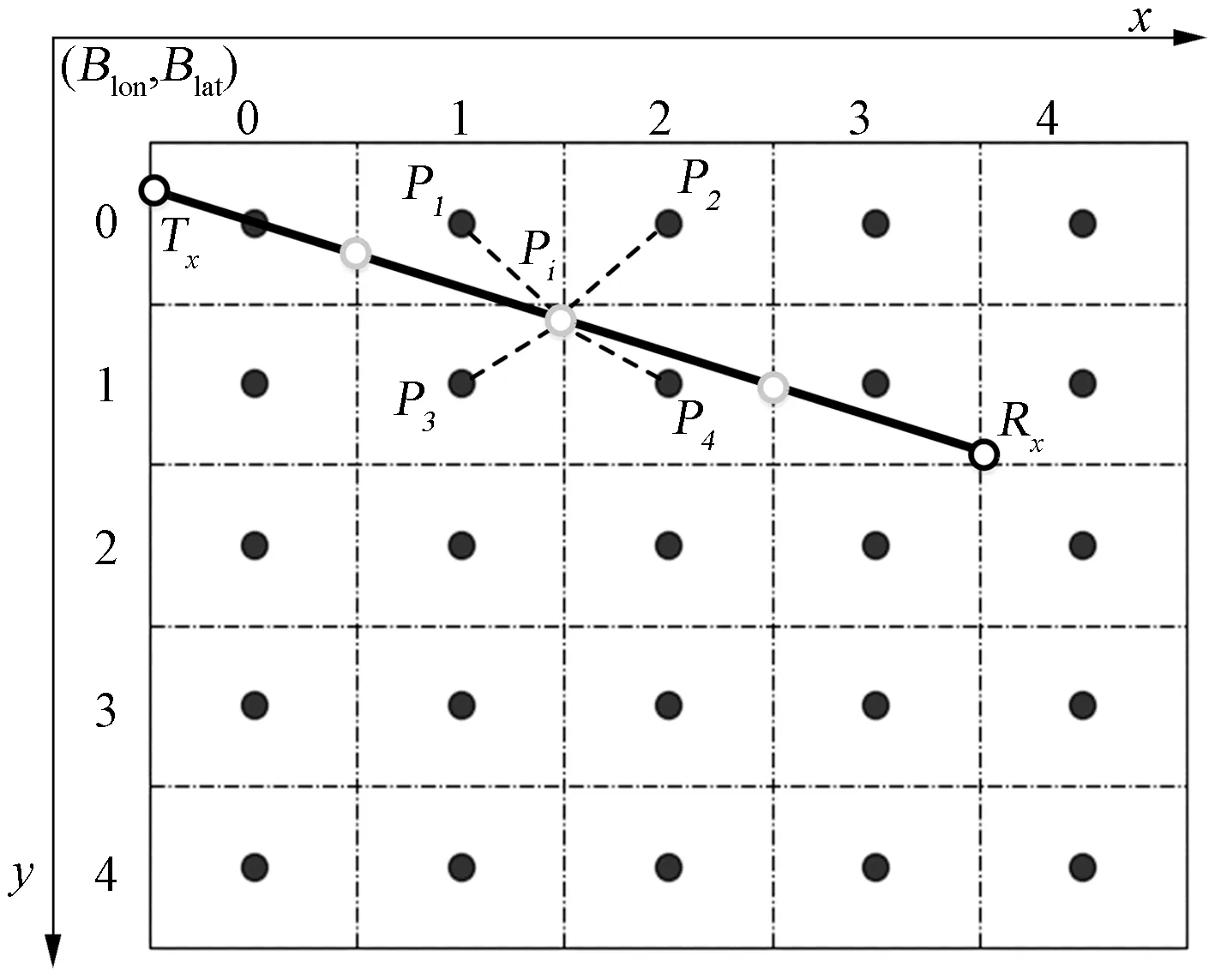
图5 IDW插值算法计算“Tx—Rx”链路中点的高程值
以图5链路“Tx—Rx”上的一点Pi的高程Hi为例,运用IDW算法的高程Hi计算思路:首先,根据Pi的经纬度计算Pi所处空间栅格位置x和y;在此基础上,判断空间栅格中与Pi点邻近相关点,分别为P1(1,0,H1),P2(2,0,H2),P3(1,1,H3)和P4(2,1,H4);接着,根据式( 8 )对栅格坐标经纬度进行逆变换,由(x,y)得到经纬度矢量数据(Clon,Clat),并转换为弧度制单位rad,根据半正矢量Haversine公式分别求出点Pi与P1、P2、P3和P4点距离Dj(j=1,2,3,4) 。之后,根据式( 9 ),计算得到点Pi与4个样本点距离Dj的加权函数Wj。
( 9 )
式中:Wj为对第j个点的加权函数;n为对第j个有影响点的个数,设定为4;P为指定的幂值,常设定为2。
最后,通过
(10)
2.2 SWU衍射改进算法
利用SWU衍射改进算法对地形链路重要障碍物特征进行提取,将“点—点”链路中障碍物的刃峰点等效于四刃以下刃形情况,最后结合Bullington和Deygout算法得到更为准确的衍射损耗分量L(ν)。
2.2.1 相关定义
定义1轨迹点:“点—点”链路中的轨迹点用p表示,包含矢量化经度、矢量化纬度和高程,表达式为
p=(x,y,z)
(11)
式中:x,y分别为轨迹点矢量化的经度、纬度;z为高程。
定义2原始轨迹点集合:“点—点”链路中的轨迹点,按照从发射站到接收站的顺序,依次排列组建轨迹点集合,用G表示,表达式为
G={p0,p1, …,pj,…,pn}j∈[0,n]
(12)
式中:pj为“点—点”链路中从发射站到接收站第j个轨迹点位置。
定义3二维轨迹点集合:在“点—点”链路中,衍射计算只关注轨迹点距离和高程二维属性。通过公式( 9 )计算轨迹点pj与发射站轨迹点p0之间距离,来替换原始轨迹集合G中矢量化精度和纬度属性值,以实现对原始轨迹集合G进行降维,得到新的二维轨迹点集合,用T表示,表达式为
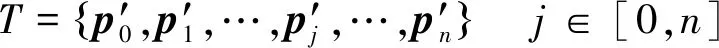
(13)
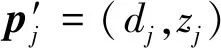
(14)
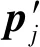
定义4第一菲涅尔滤波函数:通过第一菲涅尔区间过滤筛选得到非视距场景下障碍物轨迹点,函数方法用RF表示,表达式为
(15)
(16)
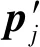
定义5障碍物轨迹集合:在二维轨迹集合T基础上进行第一菲涅尔滤波,过滤掉集合T中视距轨迹点得到的障碍物轨迹集合,用F表示,表达式为
(17)
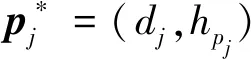
(18)

定义6单调性滤波函数:考虑刃形衍射计算中衍射损耗主要受“点—点”地形链路上刃峰点轨迹点的影响,因此通过单调性滤波函数过滤获取障碍物刃峰轨迹集合,单调性滤波函数用MF表示,表达式为
(19)
式中:
(20)
(21)
为了论述SWU的衍射改进算法,定义变量如表1所示。

表1 SWU的衍射改进算法变量及说明
2.2.2 SWU算法思想
经典滑动窗口算法(Sliding Window, SW) 通常是对一维长序列数组的遍历操作。首先,从序列起点处初始化固定大小的窗口,依次不断往窗口内加入序列中的数据,且当窗口值填满后,不断移除窗口中旧的序列数据;重复执行上述操作,移动窗口直到窗口头指针遍历到序列尾停止。
以SW与SWU算法为例,见图6。介绍对二维轨迹点集合进行滑动窗口计算,获取传播余隙hp最大值点的集合,图6中轨迹点集合为:{(0,0), (1 000,19), (1 050,20), (1 100,18), (1 150,15), (1 200,17), (1 250,33), (1 300,32), (1 350,23), (1 400,15), (1 450,33), (1 500,31), (1 550,34), (1 600,37), (1 650,22)};图6(a)中,采用经典SW算法获取二维长序列数组中传播余隙hp最大值点的集合,取轨迹点集合中传播余隙hp属性,得到轨迹点的传播余隙数组[19,20,18,15,17,33,32,23,15,33,31,34,37,22],设置滑动窗口大小为3 (实际轨迹点区间为150 m),窗口依次从左往右计算,每次取窗口内最大值maxValue加入到最大值数组中,得到最大值数组为[20,33,32,37]。该方法存在以下问题:①计算过程的单向性,窗口从左往后方向滑动,每次只单向判断合并窗口内的轨迹点计算传播余隙hp最大值点,轨迹点(1 250,33)和(1 300,32) 相邻仍然被计算在内;②未考虑到最大值数组中点与滑动窗口中轨迹点的相对位置,轨迹点(1 450,33)未被计算在内;③序列数组为一维,无法直观展示轨迹点的距离属性。
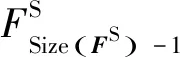

图6 SW与SWU算法
2.2.3 SWU衍射改进算法
Lee模型“点—点”模式中采用Epstein-Peterson方法计算由地形影响产生的刃形衍射损耗,该方法被证明在预测精度和计算效率方面存在不足,提出一种基于滑动窗口合并算法SWU的衍射改进算法。见图7,主要步骤如下:
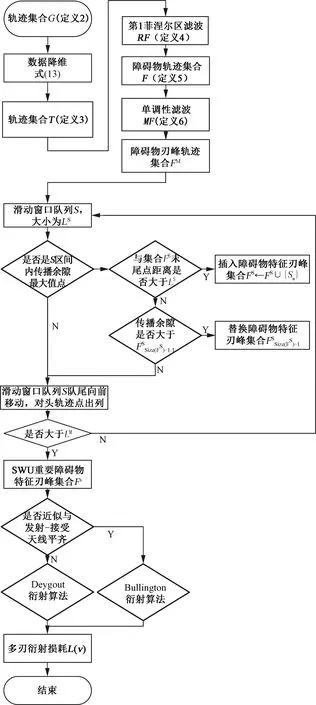
图7 基于SWU衍射改进算法流程

Step2过滤轨迹得到“点—点”地形链路障碍物数据集合FM。为实现计算机对刃形衍射的数值计算,需对“点—点”链路中轨迹点进行过滤,压缩集合中轨迹点个数,得到障碍物刃峰轨迹集合。障碍物轨迹集合F为集合T进行第一菲涅尔区间过滤筛选所得,分布情况见图8(b);之后,通过函数单调性滤波MF获取到障碍物刃峰轨迹集合FM,分布情况见图8(c)。此时,轨迹点集合已经通过过滤进行了有效压缩,大大减少了轨迹点数量且保存了“点—点”链路中刃峰点的关键特征信息。

图8 SWU衍射改进算法地形截面图分析
Step3SWU算法对“点—点”地形链路重要障碍物特征进行提取。S为滑动窗口队列,LS为滑动窗口区间大小;si为滑动窗口尾指针,指向出S轨迹点,sj为滑动窗口头指针,指向即将进入S的轨迹点;FS为重要障碍物刃峰集合。通过Step2得到刃峰轨迹集合FM,且在衍射计算过程中存在:①距离过近的两个障碍物刃峰点会产生较大衍射损耗误差;②得到刃峰点数过多,过高估计了衍射损耗影响。为此,提出了SWU算法实现对刃峰轨迹集合FM重要障碍物特征的提取,算法伪代码如算法1。

算法1: Sliding Window Union算法输入:FM:刃峰障碍物集合, LS:滑动窗口区间大小输出:FS: SWU得到的重要障碍物特征刃峰集合1: function Sliding Window Union (FM,LS)2: S←{}3: FS←{}4: LM←Size(FM)5: right,k←06: while right

Step4结合Bullington[19]算法和Deygout[20]算法进行多刃衍射损耗计算。根据SWU算法对地形链路重要障碍物特征提取后,采用Bullington和Deygout算法相结合的方式进行多刃衍射计算。当“点—点”链路为孤立山峰或多刃峰点传播余隙hp相差较大,采用Deygout算法计算单刃或等效于四刃以下刃形衍射计算;当障碍物近似与 “发射端天线—接收端天线”的齐平时,即传播余隙hp相差较小,采用Bullington方法进行计算可有效减少衍射损耗。
3 模型验证与分析
3.1 实验方案设计
为验证Lee模型“点—点”模式下的SWU的衍射改进算法的有效性,对兰州地区兰新铁路某发射站进行实验方案设计与测试,主要实验设备为中电科3900A无线接收机、高增益定向天线、全向玻璃钢GSM接收天线、5D-FB馈线和各种TNC/SMA转接头等。相关设备参数为:发射天线高45 m,接收天线高2.2 m,发射站发射功率60 W、频率932.2 MHz、天线方向角280°、天线下倾角6°、发射天线增益峰值18dBi、接收天线增益0 dBi,发射站和接收站两端馈线损耗共计7 dB。
测试方法按照国家军用标准GJB 2080—1994《接收点场强的一般测试方法》[21]要求,测试中选取接收站实测观测点数为36,观测点按照Site1—Site36进行命名。实验测试中,接收站的观测点位置选取均满足以下2个条件:①周边地势平坦,无建筑物、金属及树木遮挡场景;②如周边存在阻挡发射站—接收站连线的建筑物时,接收站位置距离阻挡建筑水平距离应大于该阻挡建筑建筑物自身高度。
3.2 模型验证
为验证Lee模型“点—点”模式衍射改进算法的准确性,引入4种模型对36组接收站观测点的信号场强观测值进行比较以验证模型准确性,分别为
模型1:Lee模型“点—区域”模式。
模型2:Lee模型“点—点”模式基础上,采用Bullington方法计算衍射损耗。
模型3:Lee模型“点—点”模式基础上,采用Epstein-Peterson方法计算衍射损耗。
模型4:Lee模型“点—点”模式基础上,采用SWU衍射改进算法计算衍射损耗。
实验观测值和4种模型预测值如表2所示,为验证模型准确性,本文引入均方根误差法RMSE,该方法为衡量观测值与模型预测值之间的偏差常用的方法之一。此外,为防止RMSE法在特殊情况下,其离散程度受其异常值影响较大对评价造成影响,本文又引入平均绝对误差法MAE,通过2种方法综合对比分析,来评价观测值与模型预测值误差的实际情况。
利用RMSE、MAE对比4种模型的预测精确性,结果如表3所示。在验证分析过程中,文本考虑样本测试数据全集(LoS+N-LoS)和非视距多山地形N-LoS两种场景情况,以验证Lee模型“点—点”模式下的SWU的衍射改进算法在通用场景和多山地形场景下的适用性和准确性。由表3可知,在2种场景下,算法得到的均方根误差均值和平均绝对误差值均最低,表明其预测精度最好,在西北多山地区场景下具有较好的适用性且准确性较高。受实验测试环境影响,定点测试观测值数量有限,也在一定程度上限制了SWU衍射改进算法的精度。在大量测试数据情况下,能够更好地反应当地环境场景Pr0和γ的取值,以及更高分辨率DEM的数据都将SWU衍射改进算法的精确度进一步提升。

表2 实验观测值与4种不同预测模型对比

表3 4种模型的RMSE和MAE dB
3.3 可视化分析
针对铁路场景的实际需求,在Anaconda python3.8环境下编程实现Lee模型“点—点”模式下SWU衍射改进算法,并采用Leaflet.js、HTML5、Vue3.js等WebGIS技术设计实现了基于Lee模型“点—点”模式下SWU的无线信号覆盖可视化预测模块。在发射站三维天线辐射方向图和DEM数据基础上,对第3节实验场景发射站进行可视化仿真,进一步对比验证模型的准确性。
图9为兰州周边某发射基站天线辐射图3D可视化仿真图,图9(a)、图9(b)为根据天线厂家(发射天线型号为DX-790-960-65-18i-0F板状定向天线)提供的水平和垂直二维辐射方向图,对天线增益辐射进行空间插值计算,得到的天线三维辐射图方向图9(c)。通过天线三维辐射图方向图,能够准确获取到不同天线水平方向角和下倾角情况下的天线增益,从而更加准确得到无线信号覆盖预测结果。在此基础上,图10 (a) 展示了第3.2节中发射站的无线信号覆盖边界的可视化仿真结果,图10(b)展示了该发射站无线信号覆盖区域的空间分布可视化仿真结果,结合3.2节中接收站36个观测点的信号场强观测值对比分析,结果表明:本文可视化仿真方法实现了对发射站、接收站、传输路径、不同地形条件下接收信号场强的可视化仿真,从而可协助决策人员对发射站的整体空间覆盖情况进行判断和分析,以实现对最佳发射功率和覆盖范围的设置,有效优化和提升站点的部署工作。
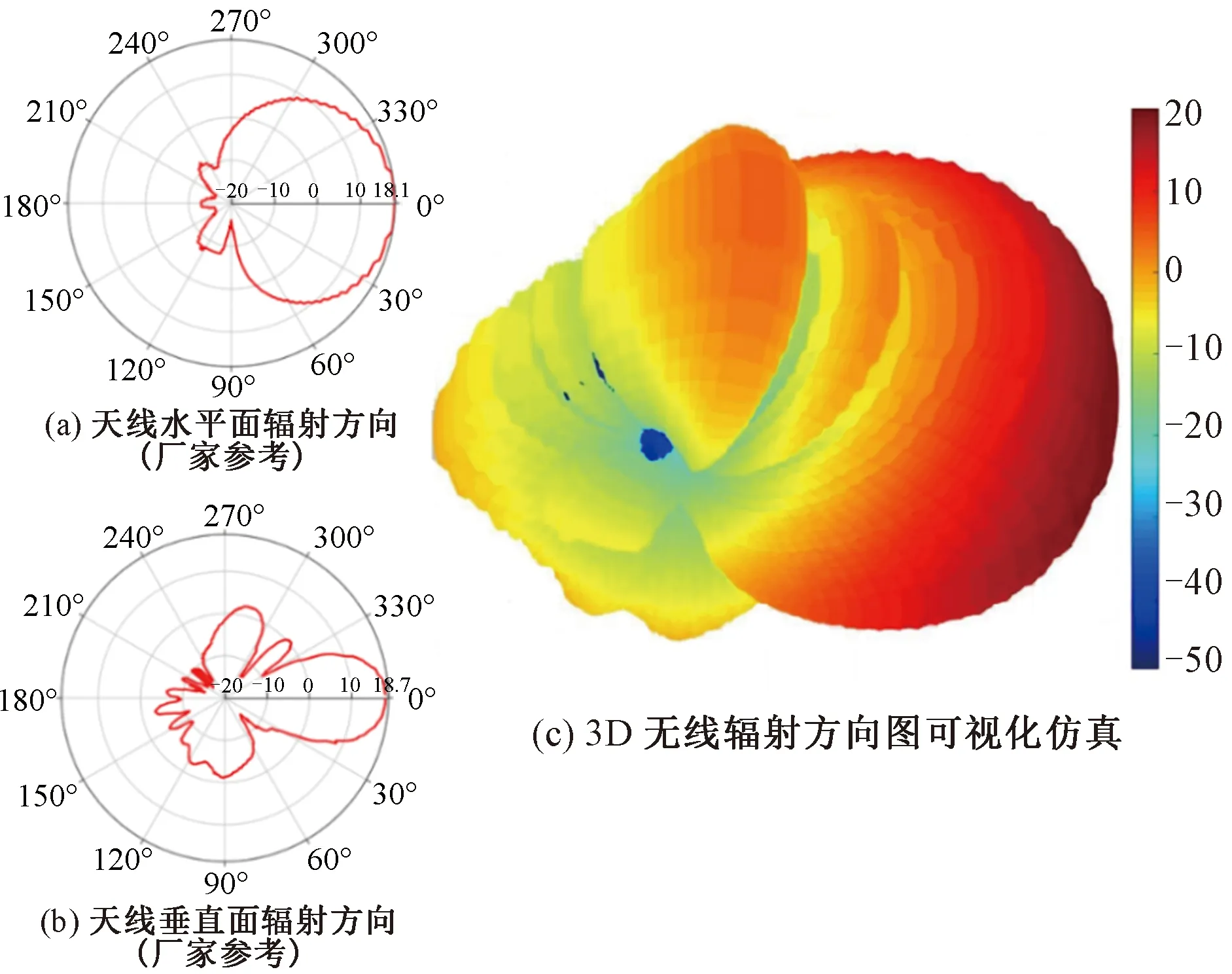
图9 兰州周边某发射基站天线辐射图3D可视化仿真(单位:dBi)

图10 发射站信号空间覆盖可视化
4 结论
对不同频段下电波传播特性展开分析,并对Lee模型“点—点”模式算法进行了深入研究,首次提出了一种基于SWU衍射改进算法。实验测试分析发现:此改进算法在非视距N-LoS情况下RMSE值为7.23 dB,MAE值为5.88 dB,在LoS+N-LoS情况下的RMSE值为6.74 dB,MAE值为5.38 dB,4种模型方法中对路径损耗预测的准确性最优。此外,利用JavaScript、jQuery、Leaflet.js、HTML5和Vue3.js等WebGIS技术,结合数字高程模型DEM、二维和卫星影像地图,设计复杂环境下铁路无线信号的可视化仿真模块,可实现在复杂地形条件和不同设备参数下,对发射基站区域场强值覆盖情况的空间可视化,从而满足使用者交互、分析和决策等多方面的需求。综上所述,提出了一种在复杂地形环境下针对GSM-R频段的基于SWU衍射改进算法的无线电波传播模型方法,并进行实验验证。结果表明该方法效提升了衍射损耗预测精度,预测准确性高。在此基础上,通过对无线电波传播模型进行可视化仿真,呈现结果准确、可信度较高,为管理和决策人员提供一种更加整体、形象和直观的电磁环境分析手段,并为优化和提升无线通信系统网络规划的前期预测、无线电频谱的管理和运维能力提供了有力的技术支撑,具有广泛的应用前景和实用价值。
