成网条件下基于运行图铺画的高速铁路通过能力计算研究

王宇强，魏玉光，林 枫

(1.中国铁道科学研究院集团有限公司 运输及经济研究所， 北京 100081；2.北京交通大学 交通运输学院，北京 100044)

近年来，我国高速铁路(以下简称“高铁”)迅猛发展，客运需求逐年攀升，形成了以“四纵四横”为基础的高铁路网，且我国高铁运营情况复杂，不同速度等级的本线及跨线列车混合运行，如何准确计算高铁通过能力且在有限的时空资源内开行更多的列车成为亟需解决的问题。

目前关于高铁通过能力计算的研究主要为扣除系数法[1]、平均最小列车间隔时间法[2]、计算机模拟法[3-4]和基于UIC 406的运行图压缩及加密法[5]，但现有研究或沿用既有线通过能力计算方法，或采用国外的通过能力计算法，或在计算过程中没有考虑占比较大的跨线列车，从而可能导致计算结果不够精确。高铁运行图铺画问题，可视为多商品流问题，列车作为商品占用高铁有限的时空资源，目标函数一般为最小化列车运行(等待)时间，最小化重新铺画后列车运行图与现有运行图的差异，最大化运营收益和最大化列车开行数。在解决运行图铺画问题的小规模案例时，可采用商业求解器(如CPLEX)得到精确解，但当处理大规模案例时，必须使用启发式算法或分解算法来求解模型，目前使用较多的分解算法包括：拉格朗日松弛法、ADMM、列生成法、D-W分解法等。文献[6-7]基于累计流变量模型铺画列车运行图，使用拉格朗日松弛算法求解；文献[8]构建扩展时空网络以解决周期运行图问题，采用ADMM分解算法求解；文献[9]构建整数规划模型，在铺画列车运行图的同时考虑客流需求，最后采用列生成算法求解；文献[10]提出一种整数规划模型来铺画列车运行图，旨在最大化运营收益，设计了启发式算法求解；文献[11]以最大化列车开行数为目标铺画列车运行图，构建整数规划模型，采用D-W分解法求解。

以上研究对车站因素的影响仍采用传统的简化处理方法，尤其是繁忙干线上衔接多方向的高铁枢纽，本线列车与跨线列车混合运行冲突干扰产生的影响未能得到深入研究，导致高铁列车运行图编制质量难以突破枢纽瓶颈的制约。文献[12]注意到这一问题的重要性，但未能提出具体有效的量化解决方法。文献[13]将车站设定为虚拟区间，提出基于点线一体化的高铁通过能力计算方法，在此基础上，本文研究将高铁枢纽这一虚拟区间内的通过能力利用细化为被各种列车弧占用的描述方法，以站场实际布局和列车径路疏解方式为基本依据，将不同方向列车在跨线枢纽站的冲突用车站最小列车间隔时间来表示，构建目标函数为最大化列车开行数量的整数规划模型，采用ADMM将复杂的列车组合优化问题分解为寻找单个列车的最短路问题，从而获得各方向列车在跨线枢纽接发和通过的最佳配合方式，最后得到更符合实际情况的运行图铺画结果。

1 问题描述

符号及其定义见表1。

表1 符号说明

本文进一步从优化高铁枢纽跨线列车运行组织的角度研究高铁运行图铺画问题，力求在有限的高铁时空资源中开行更多列车，进而计算高铁通过能力。高铁物理网(N,L)见图1(a)，包括车站集合N和运行区段集合L。为方便表示列车在物理网中的各种作业过程，采用文献[13]提出的方法构建虚拟区间，将一个车站拆分为若干物理点，将物理网扩展为服务网(N′,A)，扩展后的高铁服务网见图1(b)，包括物理点集合N′和物理弧集合A，列车在服务网中的作业过程(列车停站、列车运行和列车跨线等)为弧(i,j)∈A，表示列车从物理点i∈N′到物理点j∈N′。将起点站拆分为列车虚拟起点、列车到达点和列车出发点；将终点站拆分为列车到达点、列车出发点和列车虚拟终点；将其他车站拆分为列车虚拟起点、列车到达点、列车出发点和列车虚拟终点。车站的拆分过程及各类弧的构建见图1(b)，列车生成弧、列车到达弧、列车停站弧、列车跨线弧以及列车运行弧分别表示列车生成、列车消失、列车停站作业、列车跨线作业以及列车运行。跨线列车在跨线站2只能通过跨线弧到达车站4。

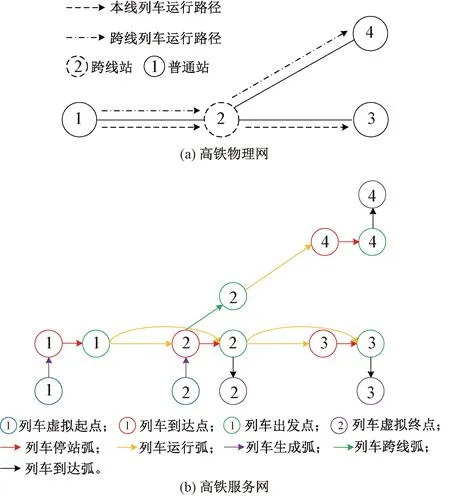
图1 高铁物理网与服务网的构建

时空网可以很好地反映列车在路网中的时空路径，被广泛应用于列车运行图铺画研究中。本文在高铁服务网的基础上，引入时间维度，构建高铁时空网(V,A′)，其中V由物理点i∈N′扩展为时空顶点(i,t)∈V，表示列车在t时刻位于物理点i，A′由物理弧(i,j)∈A扩展为时空弧(i,j,t,s)∈A′，表示列车由顶点(i,t)移动到顶点(j,s)，作业时间为s-t。服务网中各类物理弧可以扩展为以下5种时空弧：

为了更好地描述列车运行过程且保证模型的可行性，构建以下2种弧：

时空网中列车停站弧，列车跨线弧和列车运行弧的费用ci,j,t,s为实际作业时间，列车生成弧及列车到达弧的费用ci,j,t,s为0，列车虚拟运行弧的费用为无限大。基于图1(b)的高铁时空网中各类时空弧的构建以及不同速度等级的本线及跨线列车在时空网中的路径选择见图2，同理可构建另一方向的时空弧。

图2 时空网的构建及列车的路径选择

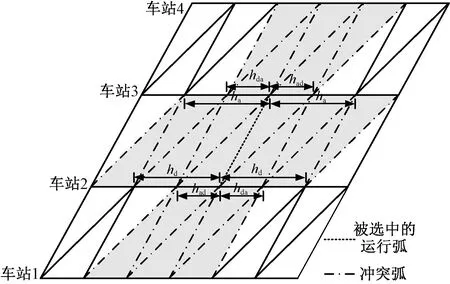
图3 冲突弧集的构建

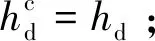
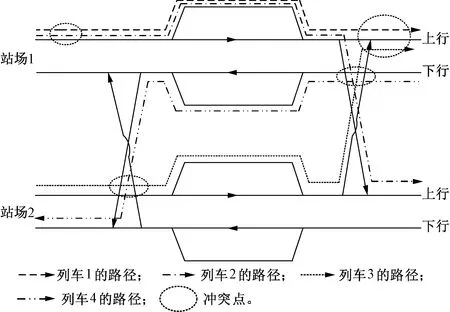
图4 跨线站站场布局及列车进路

表2 列车在跨线站的最小列车间隔时间

2 模型构建

本节基于高铁时空网构建铺画列车运行图的整数规划模型，模型的输入为：①高铁物理网；②列车开行方案；③基础数据：如列车最大最小停站时间、各种最小列车间隔时间、列车在各区间的运行时间等。模型的输出为：列车运行图、通过能力。

模型的目标函数为最大化列车选择运行弧的数量，即最大化列车开行数，即

( 1 )

为提高模型解的质量且方便算法求解，将式( 1 )转换为

( 2 )

通过阻止列车选择虚拟运行弧(即最小化列车选择时空弧的总费用)来最大化列车开行数，同时还可以最小化列车运行费用。模型的约束条件为

( 3 )

( 4 )

Depmin(k)≤DT(k)≤Depmax(k)

( 5 )

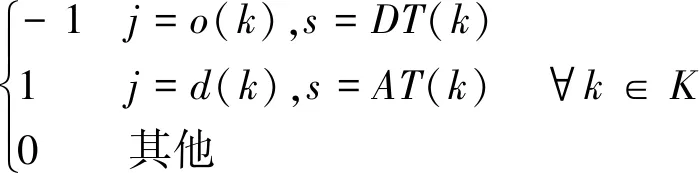
( 6 )

( 7 )

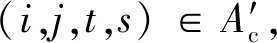
本文提出的模型为典型的NP-hard模型，复杂度较高。为直观地展示模型规模，模型中变量和各约束的数量见表3，由于式( 3 )～式( 5 )可以归并到式( 6 )中，因此式( 6 )和式( 7 )的数量见表3。

表3 模型规模

3 基于ADMM的分解算法

本文研究的列车运行图铺画问题实质上是将有限的时空资源分配给不同列车的多商品流问题，当案例规模较小时，可以使用商业求解器，如CPLEX，直接求得精确解。但当研究案例很大时，商业求解器不能在有效时间内求得最优解，所以提出使用分解算法将原问题分解为若干独立子问题进行求解。本文使用的ADMM分解算法是增广拉格朗日松弛算法与块坐标下降法的结合。其中，增广拉格朗日松弛算法是在拉格朗日松弛算法的基础上引入困难约束的二次惩罚项，可以提高模型的鲁棒性，但是二次项的引入会使模型非线性化，需要结合使用块坐标下降法处理该二次项，将运行图铺画问题分解为单个列车的最短路问题。

模型中安全约束式( 7 )会引起列车的大规模组合，其他约束都只针对单个列车。将式( 7 )作为惩罚项放入目标函数式( 2 )中，新的目标函数为

( 8 )

式中：q为弧(i,j,t,s)；ρ为二次项惩罚乘子；μq为拉格朗日惩罚乘子，其迭代方法为次梯度法，即

( 9 )

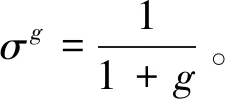
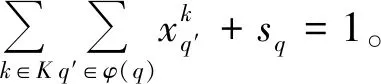
(10)

(11)

则二次惩罚项转化为

(12)

其中当πk≥1时，二次惩罚项的推导过程为

(13)

代入目标函数式( 8 )中，通过合并同类项得到

(14)

式中：Q为一个常数。

新的费用更新为

(15)

最后，经过ADMM分解的模型变为：目标函数式(14)，约束条件式( 6 )。可见新模型中各列车相互独立，原问题可被分解为若干独立的最短路子问题，各子问题可通过动态规划求解。在每次迭代求解过程中依次为列车集合K={1,2,3,…，k,…，n}中的列车寻找最短路，n为k中列车的数量，当铺画列车k的运行线时，固定其他列车的决策变量解，以此循环。

基于ADMM分解算法的步骤为：

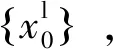
Step2通过动态规划算法为每列车寻找最短路径，用式(15)计算弧的费用，得到决策变量解集{xg}。

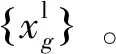
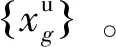
Step5使用式( 9 )更新拉格朗日乘子。

Step6如果迭代次数达到预先设定的最大迭代次数，结束算法，否则，返回Step2，g=g+1。

4 案例分析

以我国太原—德州高铁和郑州—北京高铁路网为例，同时铺画生成两条线路的本线及跨线列车运行图，验证模型及算法的可行性。提出的算法在Python平台上实现，算法运行环境为一台内存16 GB，CPU：i7-770HQ 2.80 GHz的台式计算机。

太原—德州及郑州—北京高铁共设23个车站，两条线路的交汇车站石家庄站为跨线站，10个方向的列车(太原—德州、德州—太原、郑州—北京、北京—郑州、太原—北京、北京—太原、太原—郑州、郑州—太原、郑州—德州、德州—郑州)在石家庄站可能会产生进路冲突，石家庄站的站场图及各方向列车在石家庄站的列车径路见图5，不同方向列车在石家庄站的最小列车间隔时间见表4。根据现有列车运行图，只有太原—德州、德州—太原、太原—北京、北京—太原方向有“D”字头列车，其他方向列车均为“G”字头列车，列车在各运行区段的运行时间见表5。设置案例的总时长为600 min，即时空网的时间跨度为600 min，离散化后的单位时间刻度为1 min。本文将跨线列车列入研究对象，为突出跨线列车的影响且精确量化跨线列车的开行比例，假设各列车的起点站和终点站都为太原、德州、北京和郑州，所以各方向列车数量根据现有运行图比例输入为：太原—德州7列，德州—太原7列，太原—北京18列，北京—太原18列，太原—郑州5列，郑州—太原5列，郑州—德州6列，德州—郑州6列，郑州—北京40列，北京—郑州40列。设置各最小列车间隔时间ha=3 min，hd=3 min，had=2 min，hda=2 min。

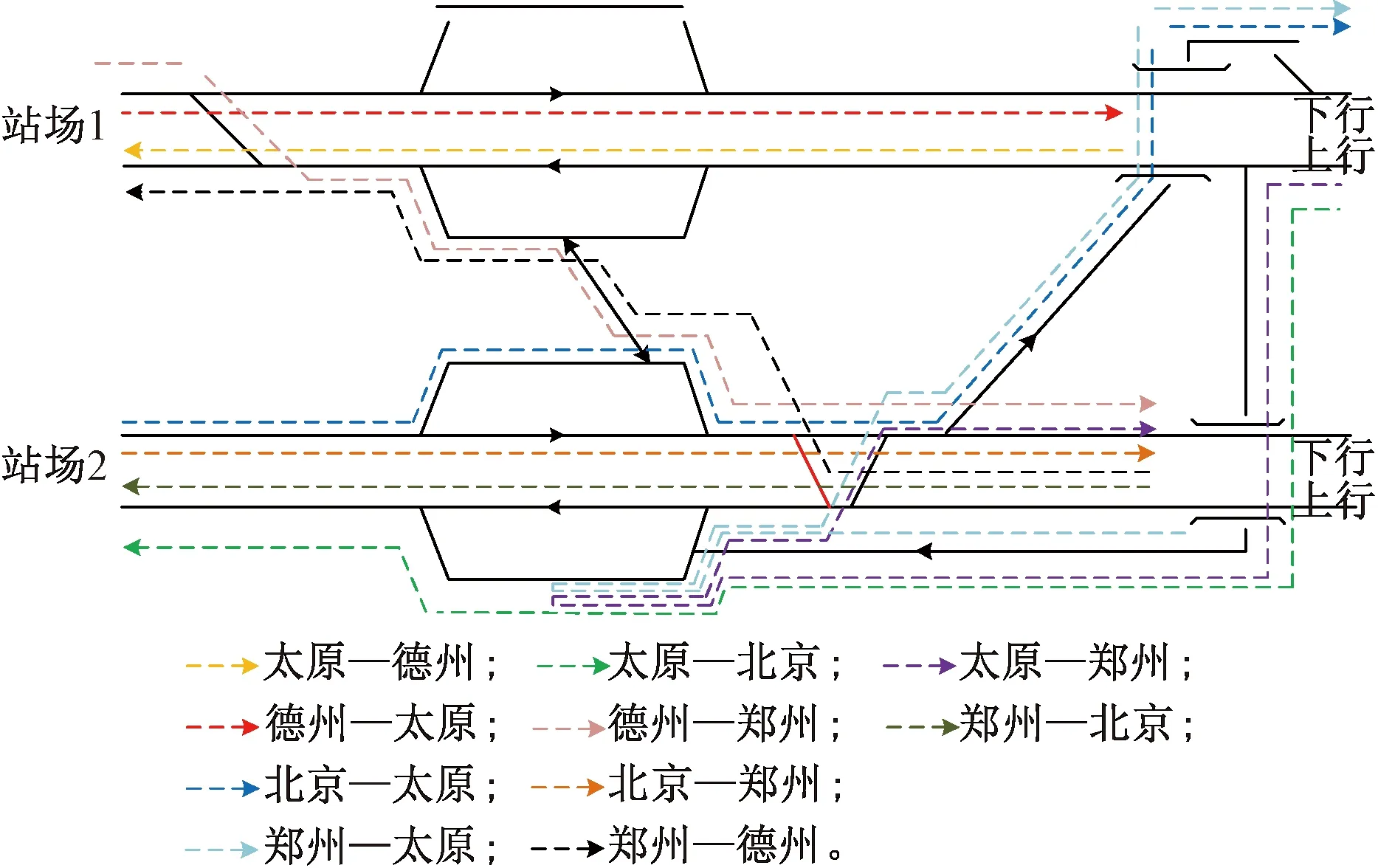
图5 石家庄站站场图及各方向列车径路

表4 不同方向列车在石家庄站的最小列车间隔时间

表5 列车在各运行区段的运行时间 min

4.1 计算结果与分析计算法的对比分析

文献[13]提出的通过能力计算方法是在已知列车开行方案和运行图的前提下用来评估当下通过能力利用情况的一种方法，计算过程较本节更为简单；而本文提出的通过能力计算方法则可根据需要，铺画出具有特定要求(如列车出发时间窗，跨线列车开行比例等)的饱和列车运行图，根据在研究时段内最多可铺画的列车数量计算通过能力，是一种可视化的通过能力计算方法，两种方法可根据需要互为补充。

图6 使用本文方法生成的高铁运行图

4.2 跨线列车比例对高铁通过能力影响分析

为了更直观的体现跨线列车对高铁通过能力及运行图的影响，研究不同跨线列车比例下不同的列车开行数量。输入列车总数固定为152列，由图6(b)可知，郑州—北京能力已趋于饱和，所以通过删除郑州—北京方向与北京—郑州方向列车，增加相应数量的跨线列车来调整跨线列车比例。图7统计了当跨线列车占分别为38%、46%、54%、62%时，600 min内可铺画的列车总数为144、138、134、132列。由于跨线列车的增加，列车在跨线站的停站时间增加，且各方向列车在跨线站的互相干扰也随之增多，造成了大量的能力消耗，可铺画列车数量降低。但从图7也可以看出可铺画列车数量减小的速度在慢慢降低，其原因是随着跨线列车的增多，具有相同属性的列车也随之增多，从而缓解了能力占用。由于跨线高铁列车一般运程较长，较运程较短的本线列车可实现更高的经济效益，因此在通过能力允许范围内，通过合理调整列车结构，适当提高跨线列车比重，可以收到更优的运营效果。

图7 不同跨线列车比例下列车开行数量

4.3 车站站场布局对高铁通过能力影响分析

本文提出的方法也可以评价高铁站站场布局,见图5，将图中红色道岔取消，郑州—德州方向列车直接改用立交形式由站场1到达站场2，那么该方向列车与太原—郑州、北京—太原、北京—郑州，德州—郑州和郑州—太原方向的列车没有冲突，计算结果见图8，600 min内太原—德州和郑州—北京高铁可铺画列车数为150列，较图6可多铺画6列列车，表明在跨线列车运行需求较大的繁忙高铁干线，合理的高铁站站场布局可减少列车进路冲突，从而提高高速铁路通过能力。

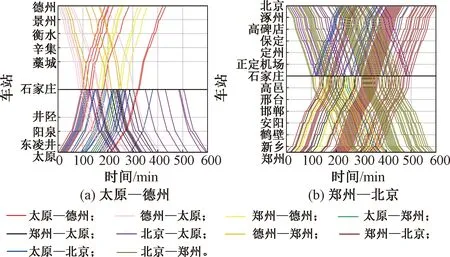
图8 站场优化后的高铁运行图

5 结论

本文深入研究了高铁枢纽内跨线列车运行对高铁通过能力和运行图铺画的影响机理。提出在跨线站不同方向列车之间的进路冲突可用最小列车间隔时间标准为判据，建立基于时空网络的整数规划模型，设计了ADMM分解算法将原问题分解为若干寻找单个列车的最短路径问题，获得了各方向列车运行线在跨线枢纽的最佳配合方案。并以太原—德州及郑州—北京高铁为例，验证了方法的可行性。论文分析、评估了跨线列车占比变化和高铁站站场布局优化对高速铁路通过能力影响，为进一步提高高铁运营效能提供了科学依据。