基于损伤-有限元全耦合法的无砟轨道CA砂浆疲劳损伤机制

邓世杰，任娟娟,3，杜 威，章恺尧，刘 伟，叶文龙

(1.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031；2.西南交通大学 土木工程学院，四川 成都 610031；3.长沙理工大学 交通运输工程学院，湖南 长沙 410114)

CRTS Ⅰ型板式无砟轨道作为我国高速铁路以及客运专线主要轨道型式之一[1]，具有良好的稳定性和平顺性，轨道结构主要由钢轨、扣件系统、轨道板、CA砂浆层以及混凝土底座板组成。其中，CA砂浆作为CRTS Ⅰ型板式无砟轨道关键部件之一，具有传递竖向荷载、协调缓冲轨道板与底座板变形差异以及调平轨道板等作用[2]。

由于无砟轨道设计年限为60 a，在服役过程中轨道将承受上千万次甚至上亿次的列车荷载作用，CA砂浆层容易发生疲劳破坏。已有不少学者围绕CA砂浆的疲劳寿命展开了研究：一方面多数研究通过室内试验研究CA砂浆寿命影响因素，建立了相应的疲劳方程或获取疲劳开裂特性[3-7]，但是试验所需费用和时间成本较大；另一方面，部分学者从连续介质损伤力学理论出发，推导了CA砂浆疲劳损伤本构模型[8-9]，较好的描述了受一定次数疲劳荷载作用下CA砂浆的全应力-应变关系，分析了砂浆受损后轨道系统的变形情况，但并没有细致探讨CA砂浆损伤过程与砂浆层应力场的变化关系。也有学者在前人基础上对CA砂浆的疲劳问题进行主要参数影响分析，并借助有限元软件得到了不同线路条件或材料不同劣化程度对疲劳寿命的影响[10-14]。

目前针对CA砂浆的疲劳损伤使用较普遍的还是Palmgren-Miner线性损伤准则，使设计寿命偏保守。在使用线性准则分析CA砂浆疲劳问题时，几乎均是首先获取正常状态下结构的应力状态，然后借助S-N曲线得到结构受力最不利位置处的疲劳寿命。这种分析方法实际上是一种从荷载应力与疲劳损伤两个角度分别独立分析的全解耦方法。然而在无砟轨道结构承受千万甚至上亿次列车荷载过程中，疲劳损伤累积到一定程度后各截面损伤不一致势必造成轨道结构部件应力应变的重分布，而全解耦方法没有考虑损伤对应力分布的影响，因此在疲劳损伤累积一段时间后其计算结果将产生一定的误差[15]。究其根本：现有结构分析有限元软件没有现成的关于耦合线性损伤准则条件下的CA砂浆疲劳损伤本构模型，若进行耦合损伤分析需要进行二次开发。

为此，本文将Palmgren-Miner疲劳损伤累积模型引入CA砂浆本构中进行二次开发，研究损伤-有限元耦合技术下CRTS Ⅰ型板式无砟轨道CA砂浆的疲劳损伤演化规律，为无砟轨道全生命周期设计提供一定的理论依据。应用该方法可较方便地推广到无砟轨道各个部件疲劳损伤分析中。

1 线性疲劳损伤模型

Palmgren-Miner线性疲劳损伤累积模型由于在工程中更加偏于安全而常用于结构寿命计算中，不少商业软件也基于该模型开发了疲劳分析模块，但更多关注在一定应力水平下结构的最终寿命，未考虑损伤的发展对构件应力状态以及寿命的持续影响。

德国人Wöhler[16]首次提出了S-N曲线的概念并一直沿用至今，一般形式可表示为

S=a+blgNf

( 1 )

式中：S为应力水平，是材料所受应力与其强度的比值；a、b为材料参数，可根据试验回归数据获取，由文献[3]可得到低弹模CA砂浆疲劳方程参数a=1.338 8，b=-0.102 07；Nf为疲劳寿命，材料的强度为2.278 MPa。

由于列车荷载属于变幅加载情况，将各应力水平下荷载作用次数和各应力水平下的疲劳寿命倒数作为一阶张量ΔN和Nf,则材料累积损伤d可表示为

( 2 )

式中：Nf为各应力水平组成的疲劳寿命张量；Nfi为应力水平Si单独作用下的疲劳寿命；ΔNi为应力水平Si的荷载作用次数，重复指标i服从爱因斯坦求和约定进行遍历求和；tr( )为取张量的迹。

根据Lemaitre应变等效原理[17]，任何受到损伤的材料在任意应力状态下都可以通过无损伤时的材料本构关系来表示，即

σ=(I-D):C:εe

( 3 )

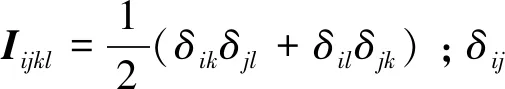
对于高周疲劳问题，材料不会出现明显的塑性变形，因此可以视其损伤为弹性损伤(ε=εe)，当材料表现为各向同性力学行为时，I：C=C，其损伤可简化为标量，即

σ=(1-d)C:ε

( 4 )

将式( 2 )带入式( 4 )可得

( 5 )

2 CA砂浆材料子程序开发与验证

采用全耦合的方法进行无砟轨道CA砂浆层疲劳损伤分析大幅地增加了计算代价。考虑到单次或者若干次的疲劳损伤累积作用不明显，可利用开发的子程序实现每隔规定循环作用次数重新更新单元刚度矩阵，以减少输出结果，缩短计算时间。在材料子程序中，单元刚度矩阵在每个增量步中都被调用，然后根据定义的疲劳损伤演化法则对损伤引起的材料刚度退化进行更新，进而描述耦合损伤的CA砂浆疲劳损伤行为。

2.1 材料子程序编制

为得到损伤变量、应力变化情况以及荷载循环次数等信息，需要将其赋予在状态变量数组中，为下一轮荷载循环作用疲劳损伤与Jacobian矩阵更新做准备。由于材料子程序在每一增量步后均要更新应力状态，因此比较方便的办法是在一个分析步中设置若干增量步，每3个增量步来形成一轮加卸载循环，但是由于增量步设置中相邻增量步变化比较剧烈，常常会导致计算不收敛。为了增加收敛性，模型建立了若干分析步，相邻分析步分配不同任务：应用Fortran 77编制式(5)所示的CA砂浆高周疲劳损伤本构子程序，建立特定功能的分析步与荷载幅值曲线，以Python脚本语言自动化分配不同分析步的作用功能。定义偶数分析步时，增量步小于0.5时为卸载功能，此时损伤本构子程序将损伤变量指定为上一步损伤，并以此更新Jacobian矩阵；增量步大于0.5时为加载功能，疲劳损本构子程序将使用当前计算损伤值。偶数分析步储存分析结束时的荷载应力，用于下一步疲劳循环作用下应力更新；奇数分析步保持荷载不变，用于疲劳加载次数更新和疲劳损伤增量更新，用于下一步分析中加卸载过程损伤分配。其变量传递关系见表1。

表1 分析步与子程序状态变量的更新传递关系

2.2 CA砂浆疲劳损伤本构嵌入验证

为验证所编写的材料子程序正确性，首先采用单个单元进行验证，为保证计算精度，单元类型为六面体二十节点，采用位移加载模式在顶面Y方向施加-0.005 5 m的位移荷载，在三个相邻面分别施加垂向约束。子程序给定参数见表2。

表2 单元验证材料参数

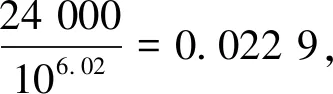
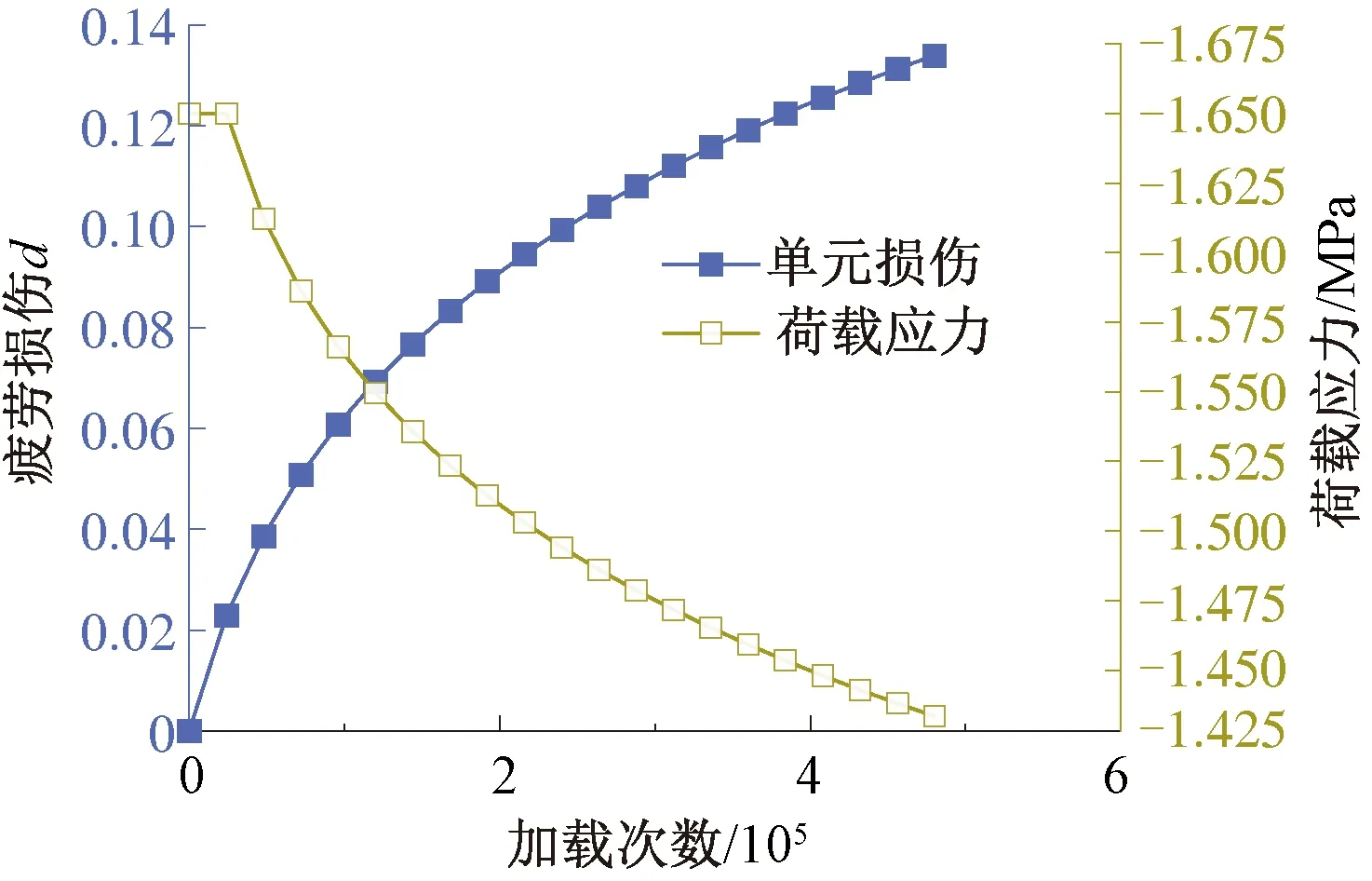
图1 单元损伤与荷载应力随加载次数的变化曲线

3 损伤-有限元全耦合技术下的无砟轨道CA砂浆疲劳损伤模型

将编制成功的材料子程序嵌入无砟轨道有限元模型中，集成损伤-有限元全耦合无砟轨道高周疲劳损伤计算方法，计算不同工况下随着列车荷载加载次数增加CA砂浆层的高周疲劳损伤发展规律。计算流程为：①建立荷载-无砟轨道耦合力学模型，将编制成功的CA砂浆高周疲劳损伤子程序嵌入该力学模型，并应用Python脚本文件自动化分配特定分析步与荷载幅值，实现每两个分析步完成一次加卸载；②计算并储存当前荷载循环下结构应力状态、疲劳损伤增量等状态变量，提供给下一轮循环加载更新做准备；③判断第n个循环加载下的加卸载条件，若加载损伤增量更新，若卸载损伤增量不更新，最终确定出当前条件下的损伤累积值；④判断是否超过损伤阈值，若超过损伤累积阈值d=dmax，若没有超过，则采用计算所得损伤值；⑤更新Jacobian矩阵、更新应力应变、更新状态变量；⑥获取CA砂浆n次循环后的损伤行为。

3.1 工况设计

为明确板式无砟轨道在线路状况中的疲劳损伤累积规律，本文从砂浆层脱空、CA砂浆材料初始损伤、列车荷载以及多种因素的组合影响进行设计工况：

(1)砂浆脱空长度

通常砂浆脱空长度在1.0～1.5 m，不超过半个板长[18-19]，本文设置横向完全脱空，且脱空长度分别为0、0.3、0.6、1.2、1.6、2.0 m。

(2)CA砂浆初始损伤

通过试验和理论分析所的成果[20-21]提出CA砂浆最大抗压强度降低幅值为0.46，弹性模量最大降低了45%，CA砂浆抗压强度2.278 MPa弹性模量300 MPa。在强度小于5 MPa时，弹性模量与抗压强度近似呈线性关系[22]。一般情况下，CA砂浆的弹性模量设计参数为300 MPa，按照最大降低0.5考虑，在线性关系下本文设置材料初始参数：弹性模量300 MPa、抗压强度2.278 MPa、弹性模量250 MPa、抗压强度1.898 MPa、弹性模量200 MPa、抗压强度1.518 MPa，弹性模量150 MPa、抗压强度1.139 MPa，分别对应初始劣化0%、16.5%、33.3%、50%。

(3)列车荷载

TB 10621—2014《高速铁路设计规范》规定[23]对于设计速度为300 km/h及以上线路列车荷载动载系数取3.0，设计250 km/h线路取2.5，在进行疲劳检算时取为1.5。考虑到客货共线情况，刘学毅[24]通过理论分析建议轮重取为150 kN。综合以上荷载取值规定，确定荷载加载型式为单轴双轮，列车荷载大小分别取为140、170、200、250、300 kN。

同时，为综合考虑多种因素对CA砂浆的损伤规律的影响，本文分别针对不同列车荷载、不同纵向脱空长度以及不同CA砂浆自身初始损伤三种因素的共同影响。具体工况设置见表3。

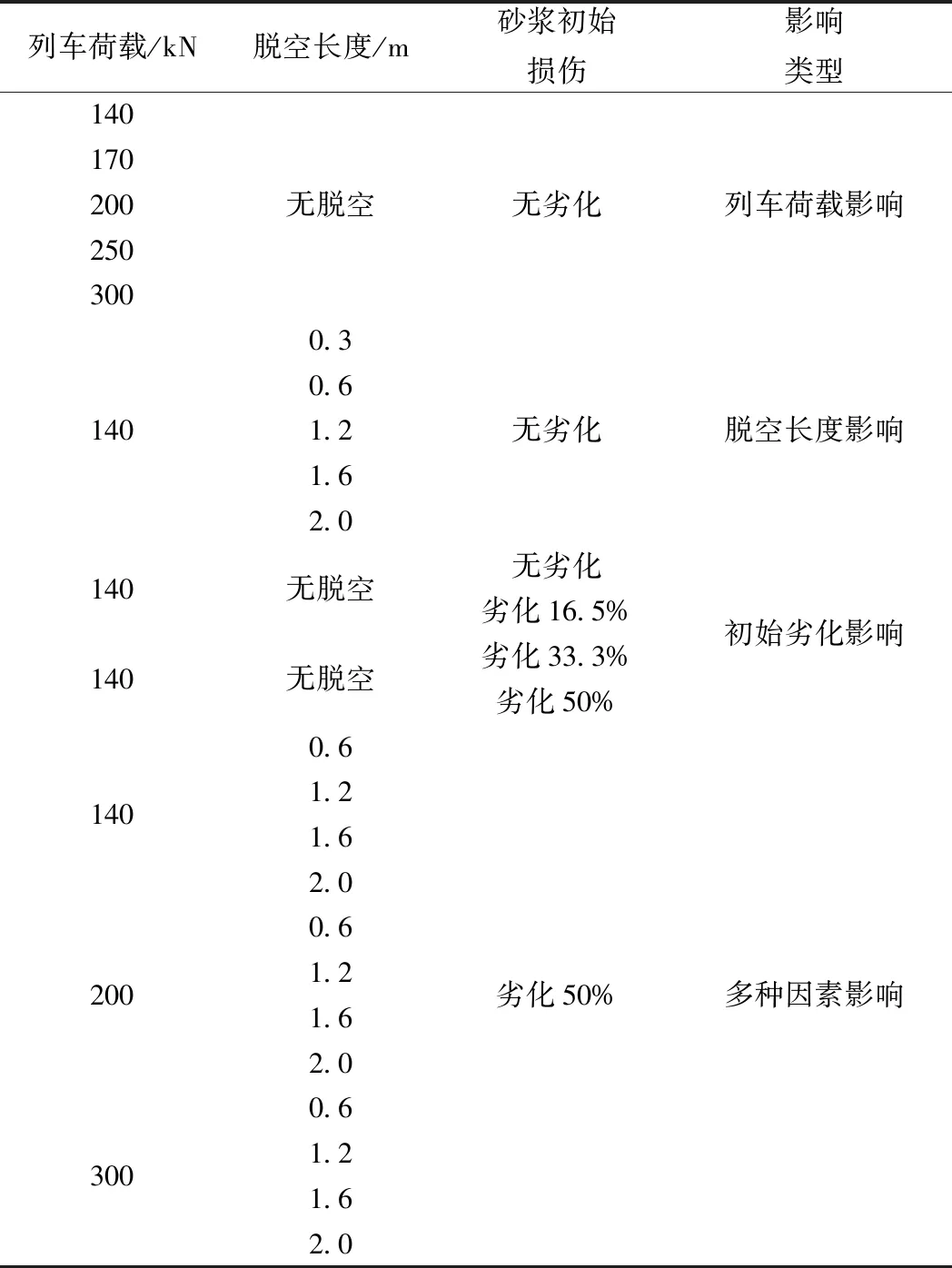
表3 组合工况设计

3.2 计算模型

CA砂浆主要承受垂向荷载，本文只考虑CA砂浆的垂向受力，在建立模型时忽略了凸形挡台。假定在设计年限内CRH2动车组为8节车厢编组，行车间隔为4 min，每天运行10 h，考虑CA砂浆因出现挤出、掉块现象，在服役期内可能被修补或换板，本模型按照10年期限加载次数1.5×107次。

模型中钢轨、轨道板及底座板采用六面体八节点实体单元，使用线弹性本构；CA砂浆采用六面体二十节点实体单元，应用本文验证成功的材料自编子程序，扣件与地基采用线性弹簧单元模拟。各部件在模型中的基本参数[25]见表4。由于模型计算设定60个分析步，为减少计算成本以及降低结果文件储存成本，模型计算结果选择关注的砂浆部件。为避免边界效应，建立5块板作为计算模型，取中间一块CA砂浆作为计算分析。

表4 CRTS Ⅰ型板式无砟轨道模型参数

4 不同工况下CA砂浆高周疲劳损伤规律

为揭示CA砂浆在无砟轨道服役过程中的疲劳损伤演化规律，对板式无砟轨道不同工况下的计算模型按照表3分别进行设置，所取点位置围绕最不利应力点(即损伤最大点)在其纵、横向分别绘制随加载次数变化的损伤累积曲线和应力变化曲线。

4.1 CRTS Ⅰ型板式无砟轨道有限元模型验证

为验证所建立的精细化模型正确性与可靠性，将模型与文献[10，26-28]中针对CA砂浆荷载应力的计算结果和试验数据进行对比，见图2。由图2可见，仿真计算的结果与文献模型以及试验测试值线性拟合线最大差距不超过0.2 MPa且规律一致，表明所建立的三维仿真模型计算结果是可靠的。

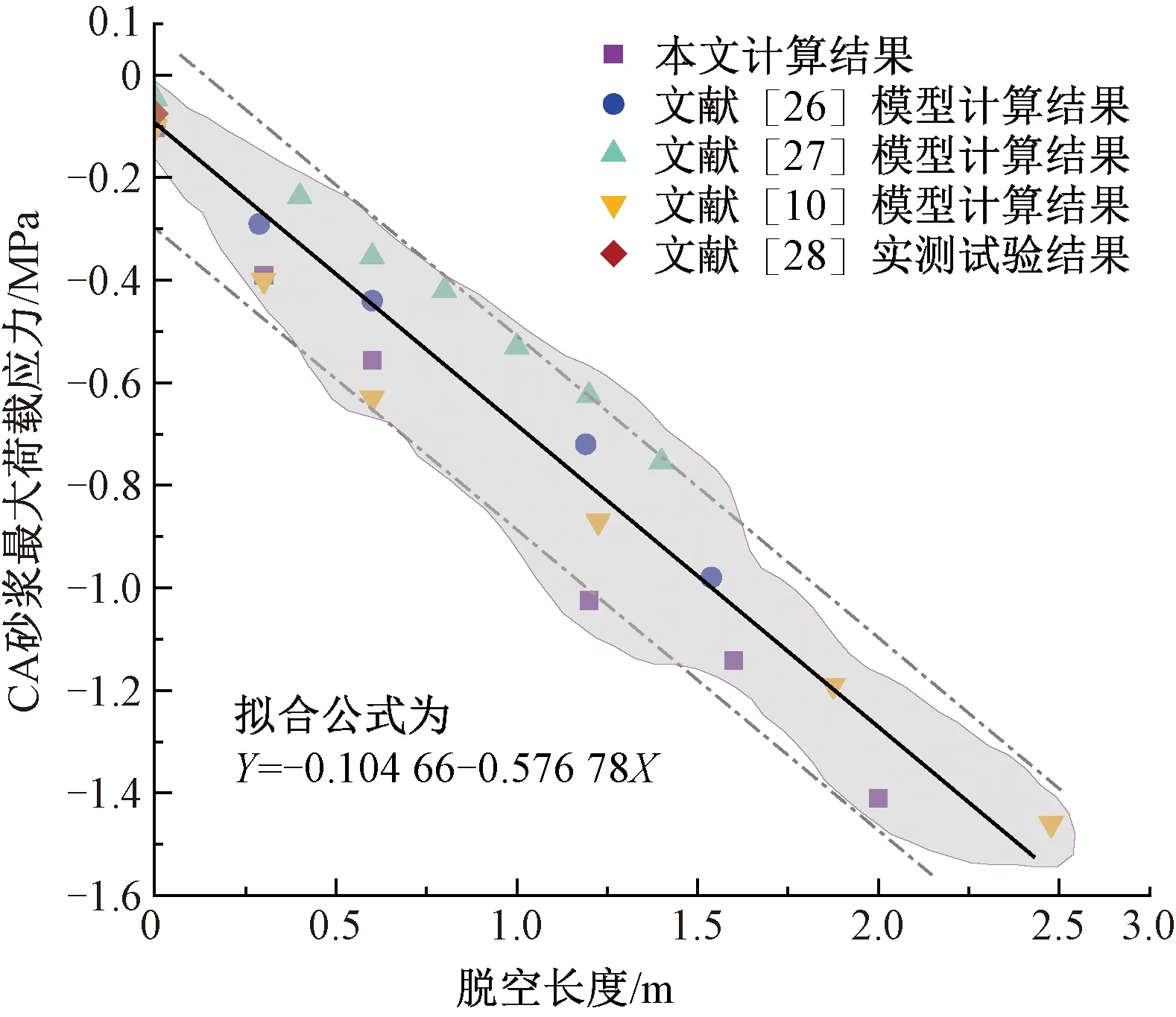
图2 仿真结果与文献数据对比

同时，模型以云图的形式描述了疲劳过程中CA砂浆疲劳损伤和剩余寿命分布情况，以CA砂浆无脱空、无初始劣化、在列车荷载140 kN工况为例，见图3。由图3可见，通过子程序的嵌入，可以直观地看出CA砂浆整体损伤累积、分布以及剩余寿命变化关系。

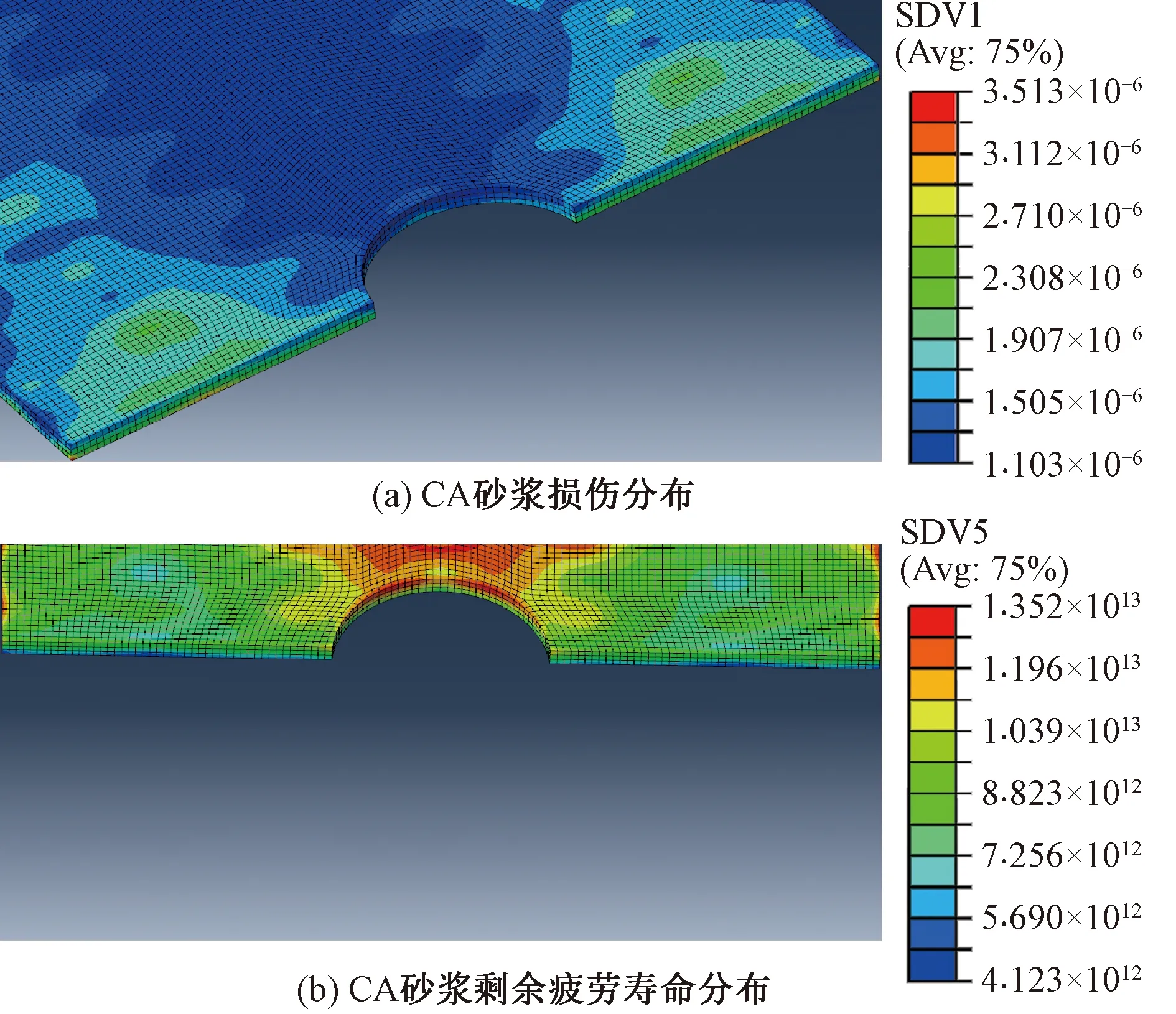
图3 CA砂浆损伤分布及剩余疲劳寿命分部

4.2 砂浆初始劣化与列车荷载对CA砂浆疲劳损伤规律的影响

当单独砂浆初始损伤或单独列车荷载变化时，计算并绘制CA砂浆疲劳损伤和荷载应力随加载次数的变化曲线(相同颜色点线和划线表示同一种工况下的疲劳损伤和荷载应力)，见图4。由图4可见，砂浆的疲劳损伤累积随着列车荷载增大而加快累积，在承受1 500万次荷载后300 kN荷载工况比140 kN的荷载工况下砂浆损伤累积仅增加了7.5×10-6。对于CA砂浆初始劣化问题，劣化50%的砂浆比无劣化的砂浆疲劳损伤累积也仅仅增加了2.3×10-6。由图4荷载应力可见，荷载应力随砂浆初始损伤加剧而逐步减小，但疲劳损伤却在逐渐加速积累，说明尽管CA砂浆降低了弹性模量使砂浆受力得到了改善，然而其强度随之减小使得所受应力水平增大造成CA砂浆在疲劳荷载作用下加速损伤。总的说来，在砂浆层没有出现脱空现象时，不论是列车荷载还是CA砂浆初始劣化，对其疲劳损伤累积规律的影响较小，所以结构荷载应力的重分布现象不明显，损伤累积呈现线性化过程。

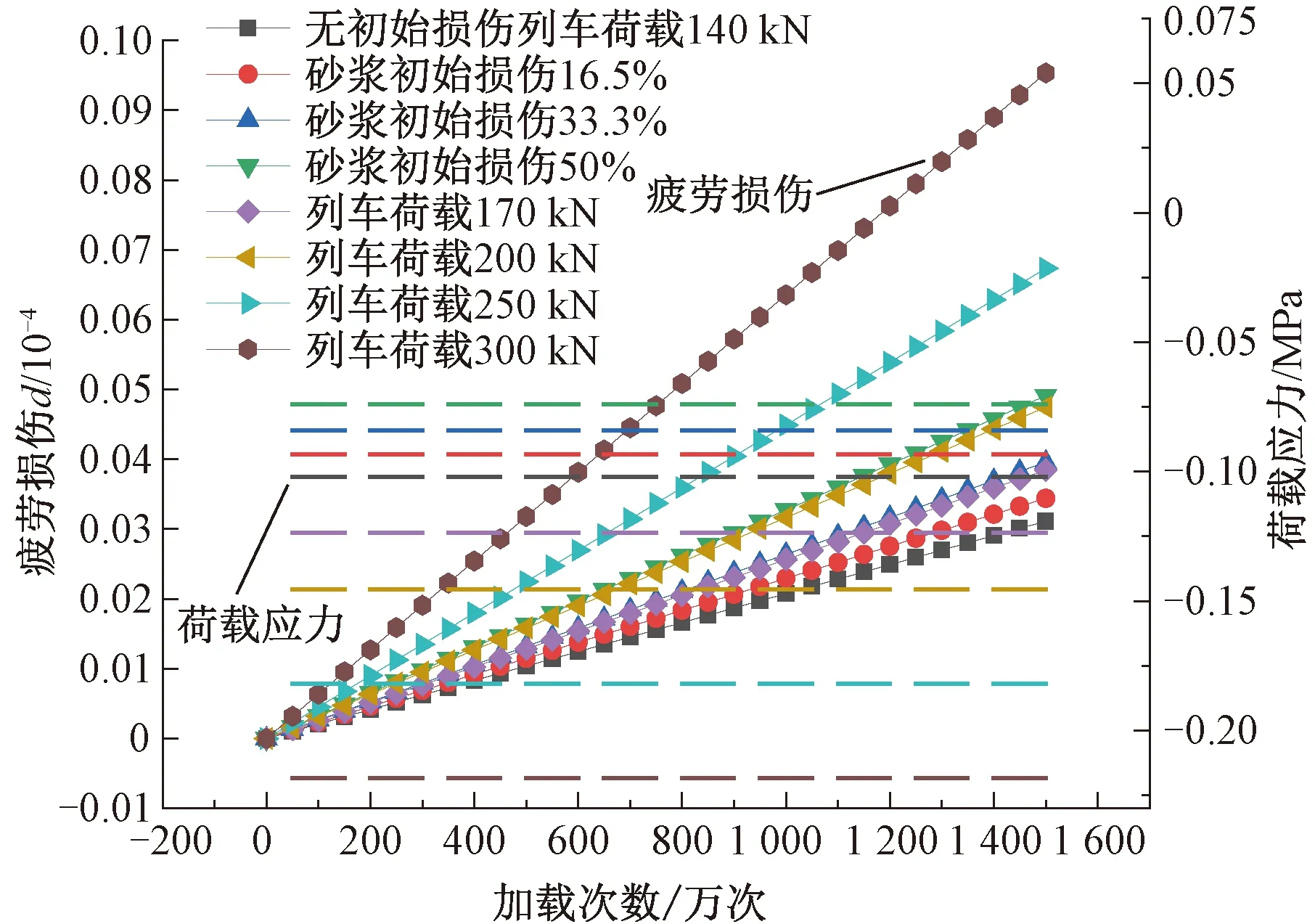
图4 CA砂浆劣化或列车荷载对CA砂浆疲劳损伤累积与应力的影响

4.3 板端脱空对CA砂浆疲劳损伤规律的影响

图5为板端脱空下CA砂浆疲劳损伤累积和砂浆应力变化曲线(相同颜色点线和划线表示同一种工况下的疲劳损伤和荷载应力)。由图5疲劳损伤可知，脱空长度0～0.6 m时CA砂浆损伤累积涨幅并不明显，结合图5荷载应力曲线可以发现，由于荷载应力较小导致砂浆疲劳损伤累积较慢，并且可以近似认为在给定服役期限内砂浆的疲劳损伤服从线性累积。脱空长度1.2～2.0 m工况下砂浆损伤累积逐步变快并且损伤加剧，非线性损伤显著体现，在脱空长度为2.0 m时最为明显。由于砂浆损伤累积到一定量值时，影响了结构的应力分布，而结构的应力分布又反过来影响了砂浆损伤的累积规律，造成CA砂浆损伤非线性增长。对于损伤非线性较为明显发展趋势的工况，在荷载作用1 500万次过程中，构件的荷载应力逐步向线性化发展，最终回落到-1.21～-1.05 MPa，相应的应力水平为0.46～0.53。

从图5 中解耦法求得的脱空2.0 m时CA砂浆疲劳损伤和荷载应力由于没有考虑损伤与应力场的耦合作用关系，导致随着加载次数的增加CA砂浆疲劳损伤累积呈线性增长，这种解耦型的计算疲劳寿命或者损伤的方法不能考虑结构时变性。本模型就在传统结构设计方法基础上，结合经验性疲劳损伤公式反映了结构在生命周期内的损伤规律，使损伤与结构力学响应耦合在一起，更真实的体现结构长期服役性能变化规律。

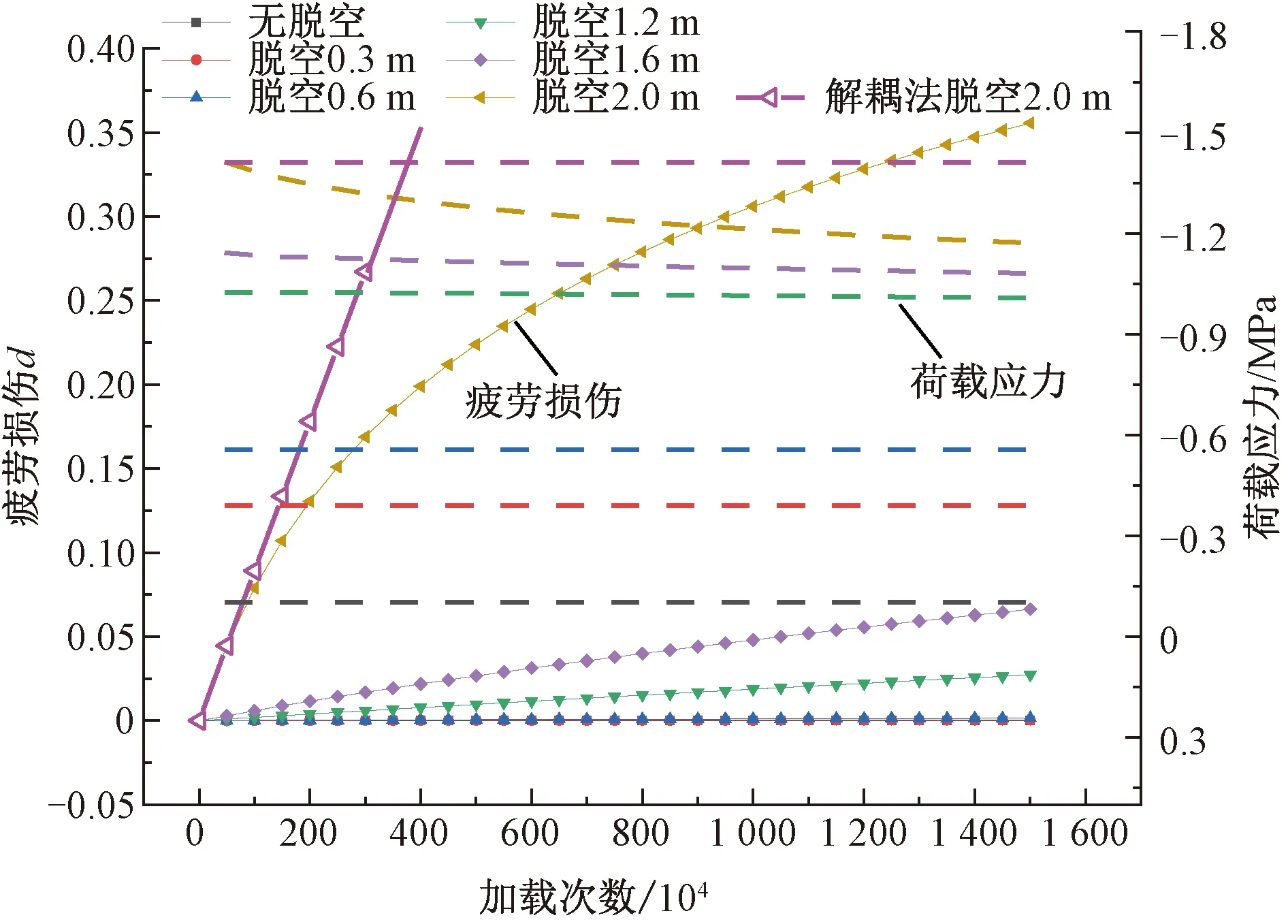
图5 脱空长度对CA砂浆疲劳损伤累积和应力的影响

脱空长度对CA砂浆疲劳损伤分布规律的影响见图6。以砂浆纵向脱空长度2.0 m、横向完全脱空下沿砂浆纵横向应力分布情况为例，纵横向应力分布取值路径见图6(a)。根据图6(b)可以看出在加载50万次到450万次时，应力最大位置为钢轨作用位置，随着加载次数的增加沿砂浆横向的应力分布逐渐均匀化，这是由于应力较大位置处损伤累积较快，力学性能较其他位置衰减较快。当超过450万次时，该位置的应力降低幅度与其他横向位置差距不明显，并且整体荷载应力降低幅度随着加载次数逐渐缩小。图6(c)为砂浆各加载阶段与50万次时的应力差值沿CA砂浆纵向分布，越靠近砂浆端部的荷载应力随着加载次数降低越剧烈，随着远离端部这种降低程度在迅速削弱，端部荷载应力的损失将分配到纵向其他位置荷载应力增加，增加幅度随着远离端部逐步减少。其他工况均服从该应力重分布规律。这一应力重分布现象在一定程度上可解释文献[29]关于无砟轨道疲劳试验中得到的“疲劳荷载使轨道板、底座板位移以及轨道板应力不同程度降低”做了一定的解释—即CA砂浆层局部损伤导致轨道结构整体应力重分布，使受力分配发生变化。说明结构的疲劳损伤需要将损伤与结构应力场耦合起来才能较为准确地描述结构的力学演化过程。

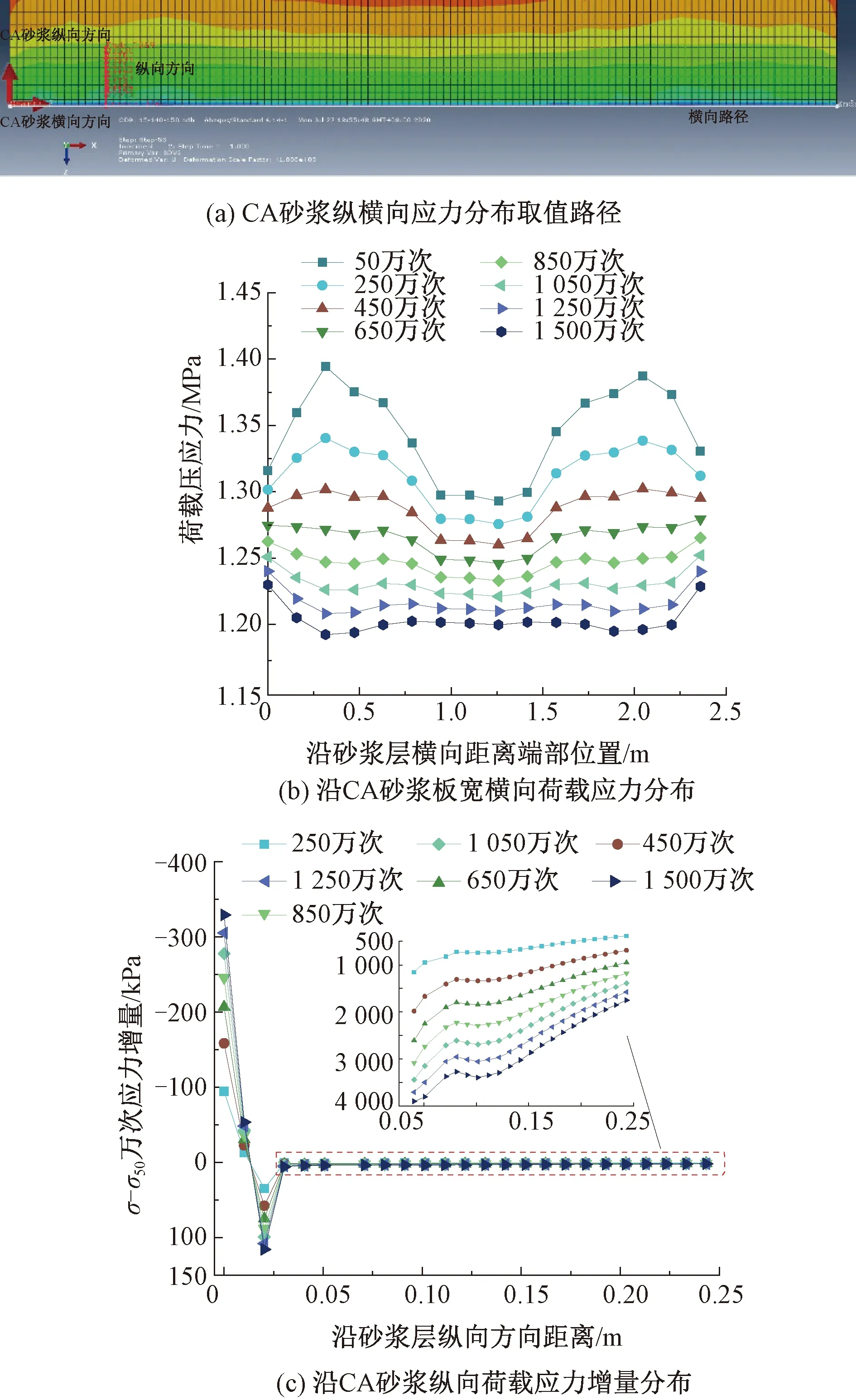
图6 脱空长度对CA砂浆疲劳损伤分布规律的影响

4.4 考虑多种因素对疲劳损伤累积规律的影响

实际线路情况CA砂浆可能已经存在一定的初始损伤，表现为弹性模量的折减和强度的降低，同时伴随着列车荷载和脱空的多重影响，为此设置CA砂浆劣化50%时本构所需的初始弹性模量和抗压强度参数(E=150 MPa，fc=1.139 MPa)，考虑不同列车荷载和脱空对CA砂浆疲劳损伤的影响规律。在混凝土的研究中混凝土在破坏前的力学性能指标存在一定值，并提出损伤达到0.635时可作为疲劳破坏判据[30]，为保障结构损伤过大造成的不收敛问题，在此定义了CA砂浆最大损伤量值为0.7。砂浆劣化50%时多种因素下砂浆层高周疲劳损伤累积曲线见图7，CA砂浆损伤累积分别从0.004增长到0.087，从0.032增长到0.529，从0.071增长到0.7(破坏)以及从0.46增长到0.7(破坏)，对应损伤增量分别为0.083、0.497，0.629以及0.24。将经历1 500万次加载的各工况最终损伤见图8，由图8可知，CA砂浆疲劳损伤在脱空长度为1.2 m时随着列车荷载的增加，砂浆损伤累积增长迅速，并且列车荷载占据主导地位；脱空1.6 m，列车荷载300 kN时，砂浆在设计加载次数内很快达到了破坏。而对于脱空长度2.0 m工况，列车荷载在140 kN时其损伤累积量值相对脱空1.2、1.6 m大了一个数量级。

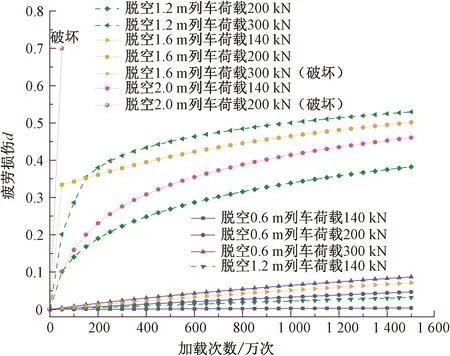
图7 砂浆初始劣化50%时多种影响因素下CA砂浆的损伤累积曲线

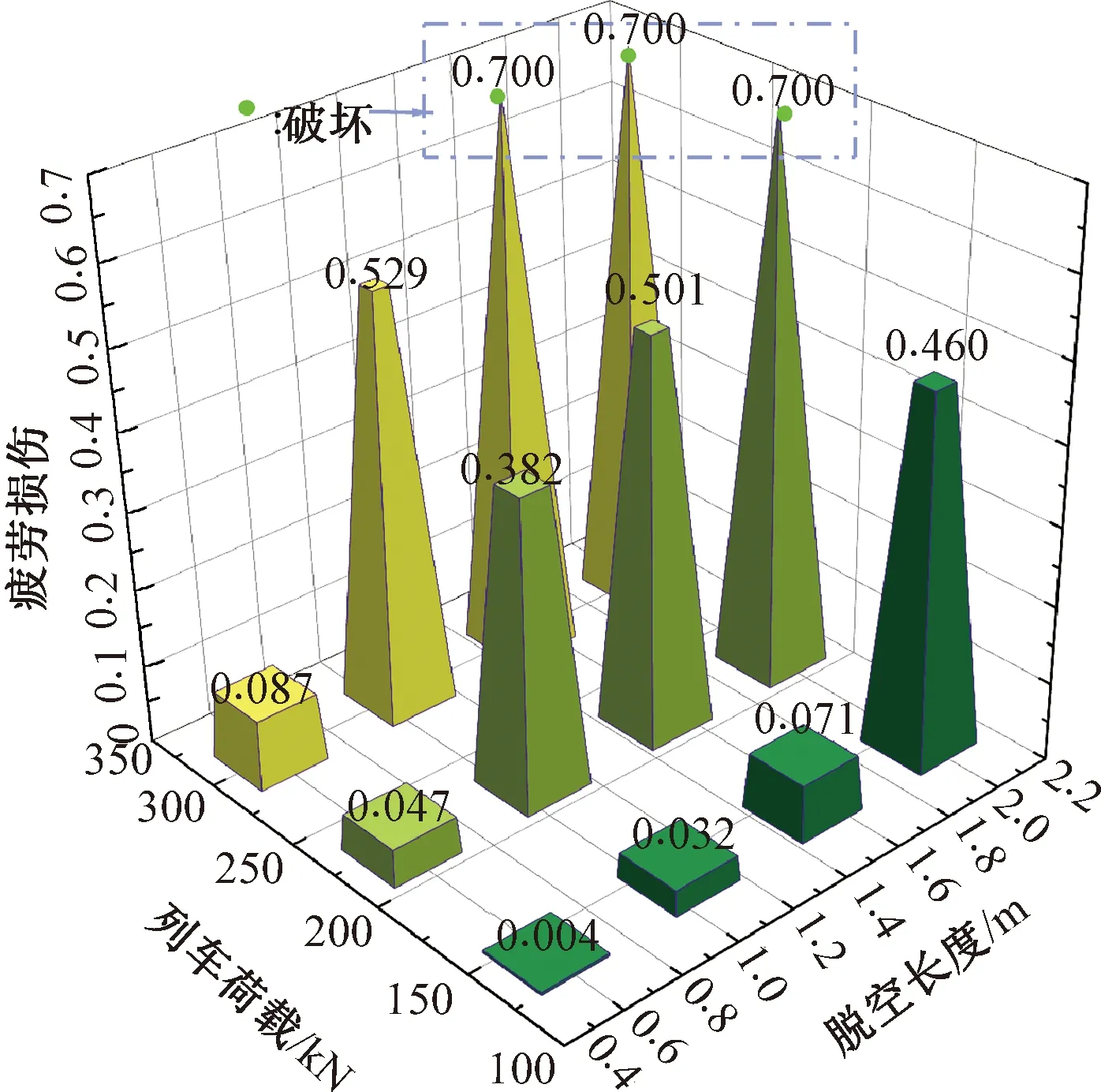
图8 1 500万次加载后不同工况疲劳损伤量值

不同工况下的荷载应力随加载次数的曲线见图9。由图9可知，脱空长度越长，列车荷载越大，应力的非线性变化越突出，并且在应力重分布过程中荷载应力逐步向线性化发展，最终趋于平稳。对于非线性强烈、构件未破坏工况下，荷载应力在经过1 500万次作用后最终在-0.55～-0.58 MPa范围内，对应初始劣化50%的CA砂浆应力水平为0.48～0.509，这与4.3节在应力水平0.46～0.53有着类似区间。说明在加载1 500万次范围内，若描述应力水平大于0.5的CA砂浆疲劳损伤演化规律，则必须要考虑由损伤引发的荷载应力重分布效应，若应力水平小于0.5，则可以忽略应力重分布对损伤累积的影响。

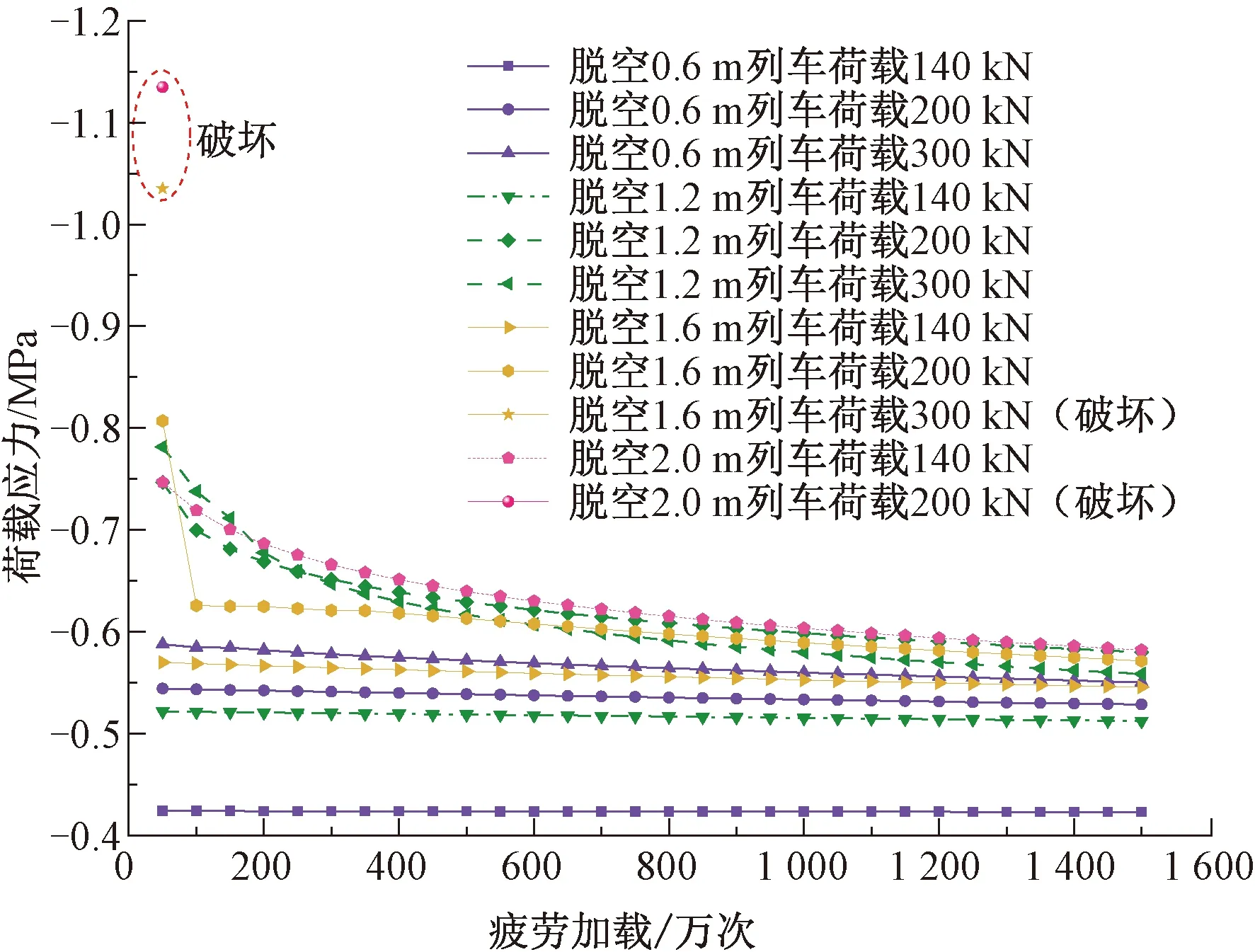
图9 砂浆初始劣化50%时多种影响因素下CA砂浆的荷载应力变化曲线

5 结论

论文通过自编程将CA砂浆疲劳方程嵌入到无砟轨道精细化有限元模型建立了损伤-有限元全耦合计算方法，诠释了无砟轨道CA砂浆层疲劳损伤累积和砂浆所受荷载应力重分布的相互影响关系，明确了CA砂浆层荷载应力场随加载次数的重分布过程，揭示了无砟轨道CA砂浆的高周疲劳损伤累积规律，得到如下结论：

(1)应用损伤-有限元耦合技术可以有效地模拟无砟轨道结构的高周疲劳损伤累积过程，并且损伤与结构应力耦合可以反映出损伤与结构应力场的相互影响机制，本文引入的全耦合方法一定程度上揭示了CRTS Ⅰ型板式无砟轨道CA砂浆层的疲劳损伤机理。

(2)CA砂浆脱空较CA砂浆初始劣化以及列车荷载变化对其损伤累积的影响突出，当砂浆无初始劣化，脱空长度大于1.2 m时，CA砂浆的非线性累积效应加剧，应力重分布现象明显。当脱空长度为2.0 m时，在1 500万次列车荷载作用下结构损伤量值已经超过了0.36，相较于未脱空条件下损伤量值增加了5个数量级。

(3)脱空长度越长，列车荷载越大，应力的非线性变化越突出，并且在应力重分布过程中荷载应力逐步向线性化发展，最终趋于平稳。沿砂浆横向其荷载应力由钢轨处明显大于其他位置到逐渐分布均匀化，而沿纵向端部荷载应力由于损伤而逐渐下降，端部荷载应力的损失将分配到纵向其他位置的荷载应力增加，增加幅度随着远离端部逐步减少。

(4)疲劳损伤累积呈现非线性的工况中，在经历了1 500万次疲劳加载后CA砂浆的荷载应力水平总是回落到0.5附近。因此在所研究的1 500万次疲劳加载范围内，应力水平0.5为是否考虑由损伤引发的荷载应力重分布效应的临界值，线性疲劳损伤在应力水平低于0.5的条件下解耦求解可靠性较高。