基于RLM-MC的高速铁路桥墩沉降曲线预测方法

龚循强，汪宏宇，鲁铁定，游 为

(1.东华理工大学 测绘工程学院，江西 南昌 330013；2.自然资源部 环鄱阳湖区域矿山环境监测与治理重点实验室，江西 南昌 330013；3.西南交通大学 地球科学与环境工程学院, 四川 成都 611756)

高速铁路桥墩施工过程中非均匀荷载，以及高速铁路运行后线路周边的环境恶化，都有可能引起高速铁路桥墩发生不均匀沉降，这势必导致轨道几何状态恶化，从而对高速铁路安全运营造成威胁[1-2]。因此，对高速铁路桥墩沉降进行严格把控，是高速铁路平稳、安全和高速运行的重要保障[3]。对于无砟轨道沉降变形监测工程，桥墩在施工后的沉降量不大于20 mm，同时应确保相邻桥墩沉降量相差不超过5 mm[4]。在高速铁路施工及运营时期进行高速铁路桥墩沉降变形监测，根据监测所得高速铁路桥墩沉降观测值，对桥墩未来沉降量进行预测，判断高速铁路桥墩是否满足规划和运营要求，为高速铁路的安全运营提供指导。

目前，沉降数据预测主要方法有曲线预测方法、灰色模型预测方法、人工神经网络预测方法等[5-6]。考虑建模复杂度以及高速铁路桥墩实际沉降规律，实际工程中主要采用曲线预测方法。其中，曲线为S形的Logistic模型能较好地反映高速铁路桥墩沉降的全过程[4,7]。Logistic模型参数估计中，通常会根据经验确定增长极限，将Logistic模型转换为线性方程求出参数的最小二乘估计。显然，这种线性化方法缺乏足够的客观性[8]。因此，可将Logistic模型参数估计看作非线性最小二乘问题，求解参数的非线性最小二乘估计，以减少主观影响。高速铁路桥墩沉降数据中异常值不可避免，而非线性最小二乘方法没有考虑观测值中所包含的异常值。因此，减弱异常值在参数估计中带来的负面影响，是提高模型预测精度的关键因素之一。

单一Logistic模型虽然能够较好地在整体上反映高速铁路桥墩沉降数据趋势，却不能在细节上反映数据波动性。

为此，采用非线性最小二乘方法中Levenberg-Marquardt(LM)法，通过引入稳健估计，建立稳健的LM(Robust LM，RLM)法，从而优化曲线模型参数和削弱异常值扰动。在此基础上，利用马尔可夫链(Markov Chain，MC)，构建马尔可夫模型，改善单一曲线模型无法有效反映高速铁路桥墩沉降数据存在随机波动的问题，从而提高预测精度。本文通过组合RLM方法和马尔可夫链，提出一种基于稳健Levenberg-Marquardt和马尔可夫链(RLM-MC)的曲线预测方法，并根据高速铁路桥墩沉降实际观测值，将本文方法与最小二乘(Least Squares，LS)法、稳健最小二乘(Robust Least Squares，RLS)法、LM法和RLM法进行比较分析，验证方法的有效性。

1 基于稳健Levenberg-Marquardt和马尔可夫链的曲线预测方法

基于稳健Levenberg-Marquardt和马尔可夫链的曲线预测方法是在曲线预测方法的基础上发展而成的。

1.1 曲线预测方法

曲线预测方法是建立在根据某种曲线函数建立模型，对预测对象历史观测数据进行拟合，从而使得模型能够描述该对象在时间推移下的变化过程。因此，选取符合高速铁路桥墩沉降规律的曲线模型和合理的拟合手段是曲线预测方法的关键。

曲线预测方法在沉降预测问题中常用的模型包括指数曲线模型、双曲线模型、Logistic模型等[9]。其中，Logistic模型又称为生长曲线模型，常用于描述事物的发生、发展和成熟三个阶段[10-11]，这种S形型的生长曲线能够较好地反映高速铁路桥墩沉降整个过程。Logistic模型计算式为

( 1 )

式中：a、b、c为待解算参数；x、y分别为观测时间、观测值。

线性化是曲线拟合的重要手段之一。通过变量代换将曲线方程线性化，依据最小二乘原理求解变换后的线性方程，再将所得线性方程转换为原曲线方程。

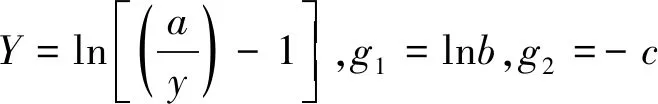
1.2 基于稳健Levenberg-Marquardt的参数估计

为使参数估计结果更具客观性，本文将Logistic模型参数估计作为一个非线性最小二乘问题。常用的非线性最小二乘方法有最速下降法、高斯-牛顿法、LM法等[12-13]。

LM法是非线性最小二乘问题广泛应用的一种算法，其结合最速下降法与高斯-牛顿法的优势，优化了迭代效率，有效解决矩阵奇异和非正定问题[14-16]。

设曲线模型f(x)的参数向量为β，则存在非线性误差方程

V=f(β)-Z

( 2 )

式中：V为残差向量；f(β)为参数β的拟合结果；Z为实际观测值组成的向量。

设βk为第k次迭代参数向量，则LM方法第k+1次迭代的参数向量βk+1为

βk+1=βk-(JTJ+uI)-1JTV

( 3 )

式中：J为V的雅可比矩阵；u为惩罚因子；I为单位矩阵。

当残差向量V中含有异常值时，会导致参数β偏离预期值。为抵抗异常值影响，本文引入稳健估计[17]，则相应的抗差解为

βk+1=βk-(JTPJ+uI)-1JTPV

( 4 )

式中：权阵P选择IGG权函数进行计算，IGG权因子计算式为[18]

( 5 )

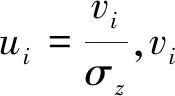
1.3 马尔可夫模型

若存在一个离散的随机过程，其时间参数是离散的集合T={0,1,2,…,t}，所对应的状态空间E=(E0,E1,E2,…,Et)，对任意时刻t(t∈T)满足：pb={pbn+1=En+1|pbn=En}，即未来n+1时刻的状态En+1仅与当前n时刻的状态En相关，而与过去的状态无关，这称为马尔可夫链的“无后效性”[19-20]。

时间序列统计量多数都具备马尔可夫性质，利用这一性质可有效提高模型的预测精度[21]。马尔可夫模型修正预测值主要过程如下所述。

(1)状态划分

根据曲线模型模拟值的相对误差大小，采用聚类方法并结合IGG权因子结果剔除异常期数，将相对误差区间分为d个状态。其中，d的计算式为

( 6 )

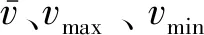
(2)状态转移概率

状态Si经一步状态转移到状态Sj的概率pbij为

( 7 )

式中：Mij为状态Si经一步转移到状态Sj的次数；Mi为Si发生一步转移的次数。

计算所有状态的状态转移概率，则其构成的矩阵为

( 8 )

式中：矩阵PB称为状态转移概率矩阵。最后根据矩阵PB和当前时刻状态Si，则可得下一时刻最可能所处的状态Sj。

(3)预测值修正

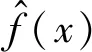
( 9 )

式中：δs为预测值所处状态对应的相对误差；x为观测时间；f(x)为原始预测值。

1.4 本文提出方法

基于RLM-MC的曲线预测方法具体流程见图1，主要步骤为：首先，使用尝试法结合黄金分割法确定参数a的估值[8]，即可利用LS方法估计曲线模型参数，再将参数的LS估值作为RLS方法迭代的初值；然后，将参数的RLS估值作为RLM方法迭代的初值，完成Logistic曲线拟合；最后，结合马尔可夫模型修正Logistic模型预测值。

图1 本文方法流程

本文方法具体计算步骤如下：

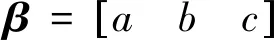
Step2计算权阵P=pW，再利用式( 2 )计算观测值残差向量。

Step3取k0=1.5、k1=2.5，根据式( 5 )确定一组新的权因子，可得权因子矩阵，进而得到新的权阵P。

Step4利用式( 4 )计算参数的稳健LM估值。

Step5重复Step2～Step4，直至JTPV≤10-10或迭代次数k大于最大迭代次数kmax(kmax通常在20～50之间选取[22-23]，本文令kmax=30)。满足条件后退出迭代，则获取参数RLM估值及曲线模型预测值。

Step6计算曲线模型模拟值相对误差，根据式(6)计算状态区间个数，通过k-means聚类并结合IGG权因子计算结果剔除异常期数，从而确定每个模拟值所处状态。

Step7以式( 7 )计算状态转移概率矩阵，预测后续状态。

Step8根据预测状态，利用式( 9 )修正曲线模型预测值，得到最终预测值。

2 试验设计

以上阐述了基于RLM-MC的曲线预测方法，为验证本文方法的有效性，采用两组高速铁路桥墩沉降观测数据进行试验，将所得结果与LS法、RLS法、LM法和RLM法的预测结果进行比较分析。

2.1 试验数据

试验使用的两组高速铁路桥墩沉降观测数据来自西安—成都某高速铁路，每组沉降观测数据包含2014—2015年20个定期沉降观测值[24]，见表1、表2。两组数据均设置1～17期为模拟区间，18～20期为预测区间。

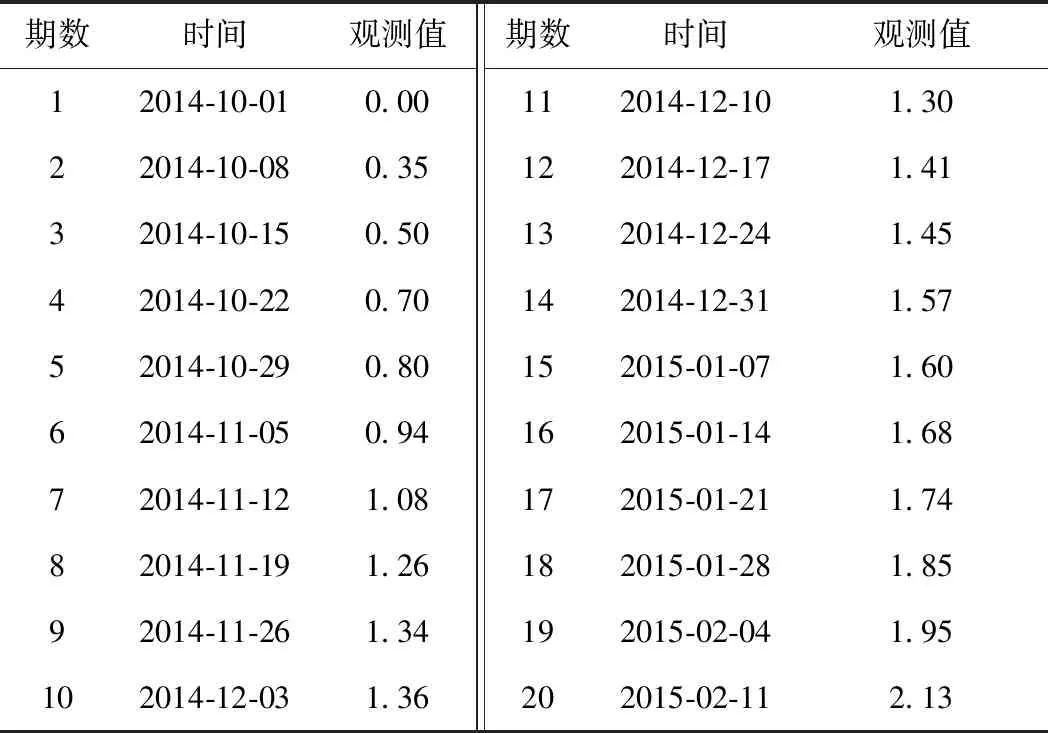
表1 第一组观测数据 mm

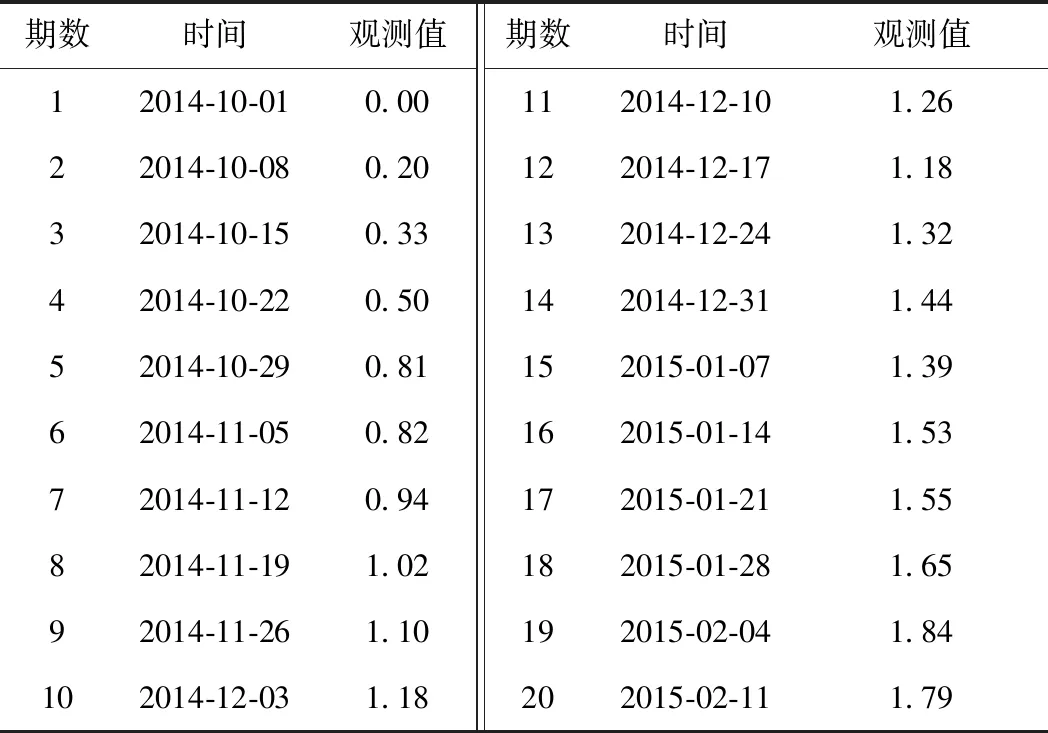
表2 第二组观测数据 mm

2.2 评定指标

对于LS、RLS、LM和RLM法的参数估计结果，使用单位权方差进行定量评估，单位权方差能反映模拟值与实际值的离散程度，从而体现参数估计结果的优劣。单位权方差越小，离散程度越小，则参数估计精度越高，单位权方差σ02计算式为

(10)

式中：n为模拟期数。

预测精度采用以下三个精度指标定量评估。平均绝对误差MAE为最基本的评定指标，概念简单易于解释，只衡量预测值误差的平均模长，直接反映预测值与真实值之间的误差情况。均方根误差RMSE相对MAE，易受偏差较大的预测值影响，导致放大RMSE的结果，因此可比较不同模型的稳定性。平均绝对百分比误差MAPE考虑了误差与真实值之间的比例，可以比较不同尺度下预测结果的好坏。

MAE、RMSE和MAPE越小，则预测结果准确度越高，其定义分别为

(11)

式中：[n+1,N]为预测区间范围；i为预测期数；zi、f(i)分别为相对应的实际观测值和预测值。

3 结果与分析

采用两组高速铁路桥墩沉降观测数据进行试验，分别利用LS、RLS、LM和RLM法进行参数估计，并通过马尔可夫模型修正RLM法预测结果。模型参数估计结果，从各方法的模型和单位权方差等方面进行比较分析，并采用MAE、RMSE和MAPE等评定指标对预测结果进行评估。

3.1 第一组试验

根据表1数据，分别利用LS、RLS、LM和RLM法对曲线预测模型进行参数估计。结合尝试法和黄金分割法计算参数a粗略估值，由于试验数据没有明显地放缓趋势，黄金分割区间的选取可略微偏大[8]，本文选取模拟区间最后一期数据设为黄金分割区间下限，并将下限值的5倍设为黄金分割区间上限，则该区间为[1.740, 8.700]。对该区间进行一次搜索的结果作为参数a的粗略估值，即a=1.74+(8.70-1.74)×0.618 ，即得到参数a的粗略估值为6.041，接着进行LS、RLS、LM和RLM法的参数估计。参数a、b、c和单位权方差σ02见表3。

表3 第一组试验各方法估计结果比较

LS与RLS法的参数a并未参与迭代运算，LS方法在不能迭代调整参数的情况下，参数a在一定程度上直接决定了参数b、c，这导致LS法b、c参数估计结果相对其他方法偏大，其单位权方差也大于其他方法。RLS法虽然不能调整参数a，但引入稳健估计后能动态调整参数b、c，单位权方差低于LS法，显然减少了参数a带来的主观影响。RLM法所得单位权方差相对LS法减少了54.545%，而RLS和LM法相对LS法仅分别减少了13.636%与6.818%。RLM法单位权方差远小于LS、RLS和LM法，在所有方法中表现最优，说明在第一组观测数据中采用RLM法进行参数估计精度更高。

得到参数a、b和c的RLM估值后，即可根据式( 1 )计算模拟值，并计算模拟值的相对误差。由于第一期沉降值为0无法计算相对误差，所以相对误差和状态划分均从第2期开始计算。

根据式( 6 )计算得出，相对误差需划分为4个状态，使用k-means聚类将相对误差分为4类(4个状态)，即可确定每期模拟值相对误差的所处状态，再结合RLM计算的权因子剔除可疑期的相对误差对聚类质心结果的影响，将每个状态的聚类质心作为其对应的相对误差。最后，得到的4个状态以及所对应的相对误差为δS1=-6.171%，δS2=14.422%，δS3=-43.387%，δS4=1.927%。每期数据的具体模拟值、权因子w和状态S划分见表4。

表4 RLM方法模拟值、权因子和状态划分

根据表4及状态转移概率矩阵可知，17期所处状态为S1，在状态转移概率矩阵中S1最有可能一步转移到S1，其概率为0.75，则可认为第18期预测值所处状态最有可能为S1。根据式( 9 )通过状态S1所对应的相对误差修正第18期预测值，同理依次可得后续预测值。各方法模拟值的残差绝对值见图2，各方法预测结果见表5。

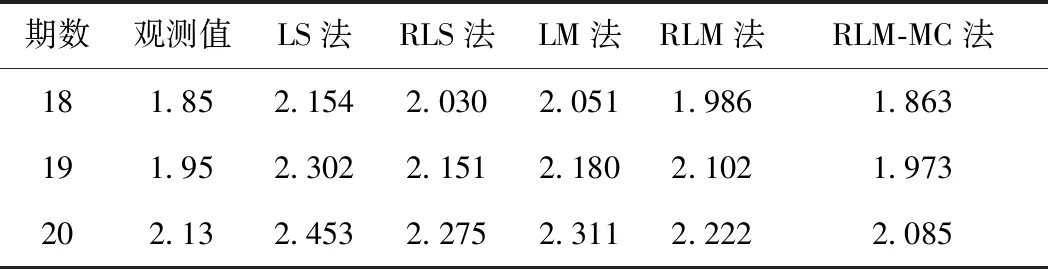
表5 第一组试验各方法预测值 mm

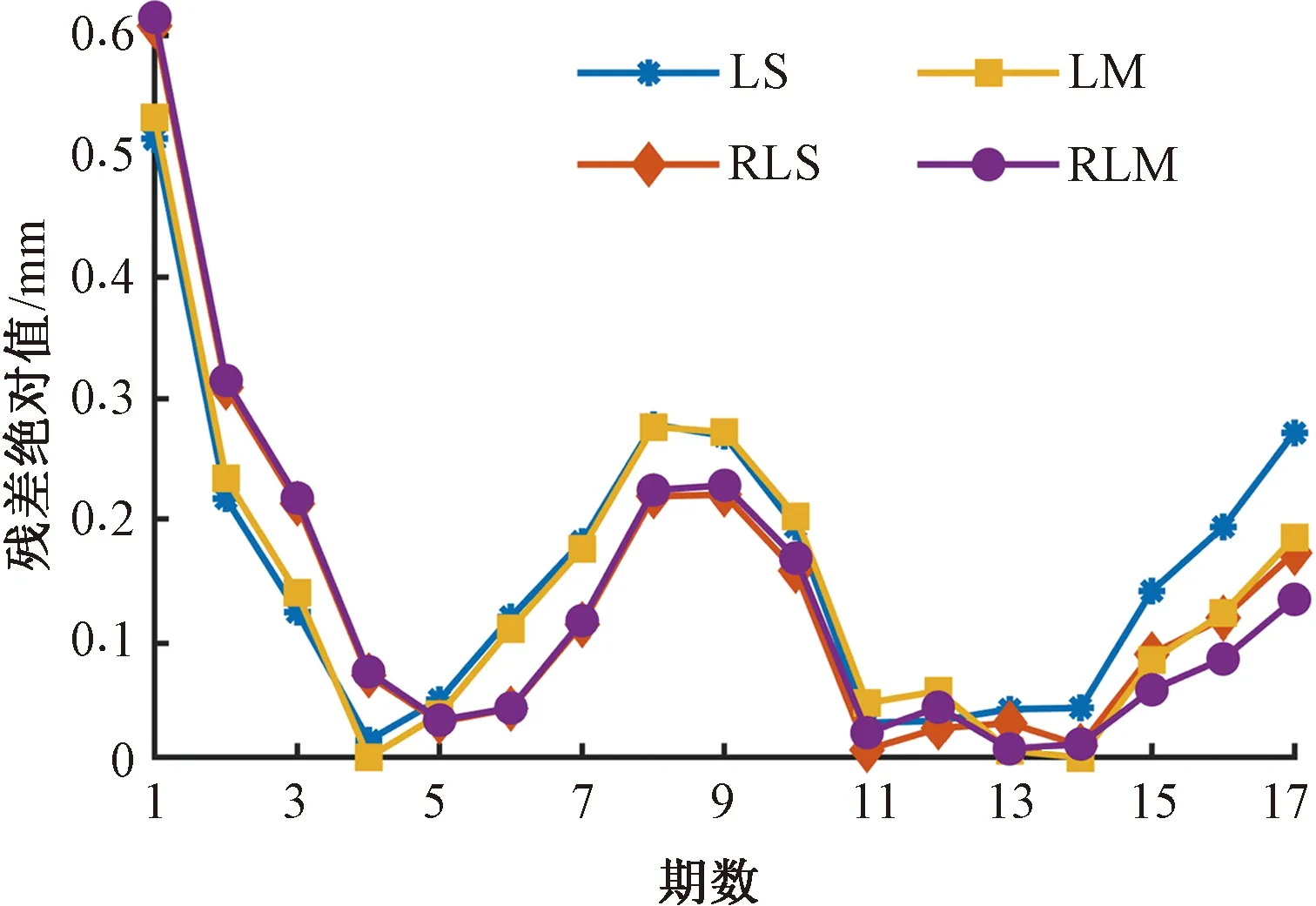
图2 第一组试验各方法模拟值的残差绝对值

由图2、表5可以看出，LS法相对其他方法在单位权方差偏大的情况下，预测结果整体变差，预测精度相对较低。RLS法因引入稳健估计，参数b、c的结果不会完全取决于参数a的估值，减少了人为主观因素影响，提高了参数估计精度，因此，预测精度相比LS方法略微提高。LM法预测结果与RLS法相近，引入稳健估计后得到的RLM法预测结果比LS法、RLS法和LM法都更接近实际观测值，并在使用马尔可夫模型修正预测值后，精度得到了进一步提高。为更直观地体现不同方法的精度变化，根据式(11)计算预测值的三个精度指标，结果见表6。

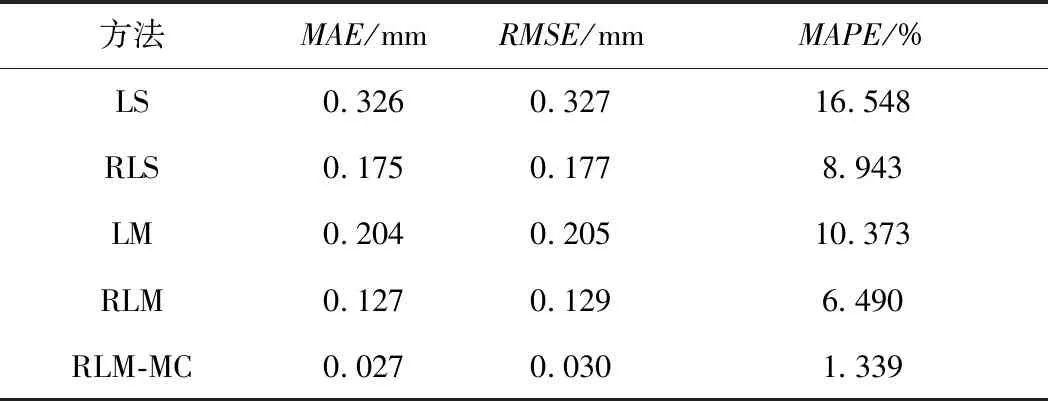
表6 第一组试验各方法预测精度指标

从表6可以看出，每种方法所得的MAE和RMSE均十分接近，这表明在第一组观测数据的试验中，没有出现相对偏差较大的预测。进一步分析可以得到，LM法比LS法的RMSE减少了37.309%，RLM法比LM法的RMSE减少了37.073%，RLM法经过马尔可夫模型进一步修正后，RLM-MC法比RLM法的RMSE减少了76.744%。本文方法相对最小二乘方法的RMSE减少了90.826%，MAPE由16.548%下降到1.339%，预测精度得到显著提高。因此，在第一组观测数据的试验中，RLM方法参数估计精度最优，并在结合马尔可夫模型后，RLM-MC法预测结果远好于其他方法，说明采用RLM-MC法进行预测更加合理。

3.2 第二组试验

根据表2数据，同样使用尝试法结合黄金分割法，确定黄金分割区间[1.550,7.750]，即得参数a=5.382。分别利用LS、RLS、LM和RLM方法对曲线预测模型进行参数估计，求出参数a、b、c和单位权方差σ02，其结果见表7。

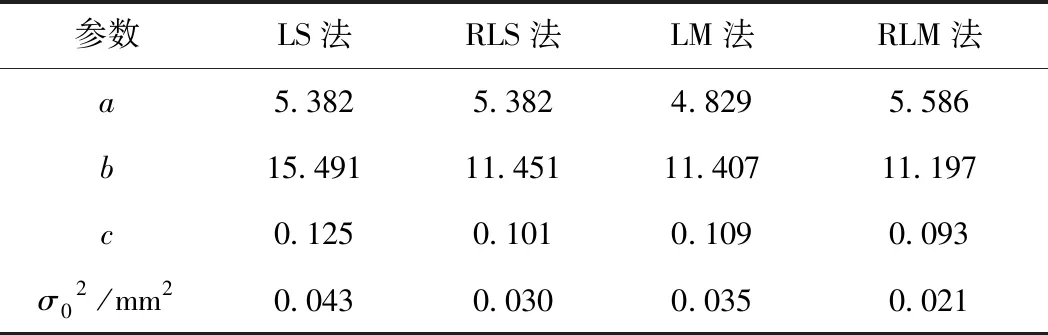
表7 第二组试验各方法的估计结果比较

在第二组观测数据中，RLS法相对LS法，RLM法相对LM方法，稳健估计均有效削弱了异常值扰动对参数估计带来的影响，其单位权方差分别减少了30.233%和40.000%。同时，比较LM法与LS、RLS法的单位权方差可以看出，LM方法单位权方差小于LS法，接近RLS法，相比LS法单位权方差减少了18.605%，说明即使未引入稳健估计，非线性最小二乘在参数估计中，仍具有一定的优越性。

同样根据式( 6 )计算得出，相对误差需划分为4个状态，使用k-means聚类将相对误差分为4类(4个状态)，则得到的4个状态以及所对应的相对误差为S1=-28.287%，S2=12.127%，S3=-2.663%，S4=78.883%。每期数据的具体模拟值、权因子和状态划分见表8。

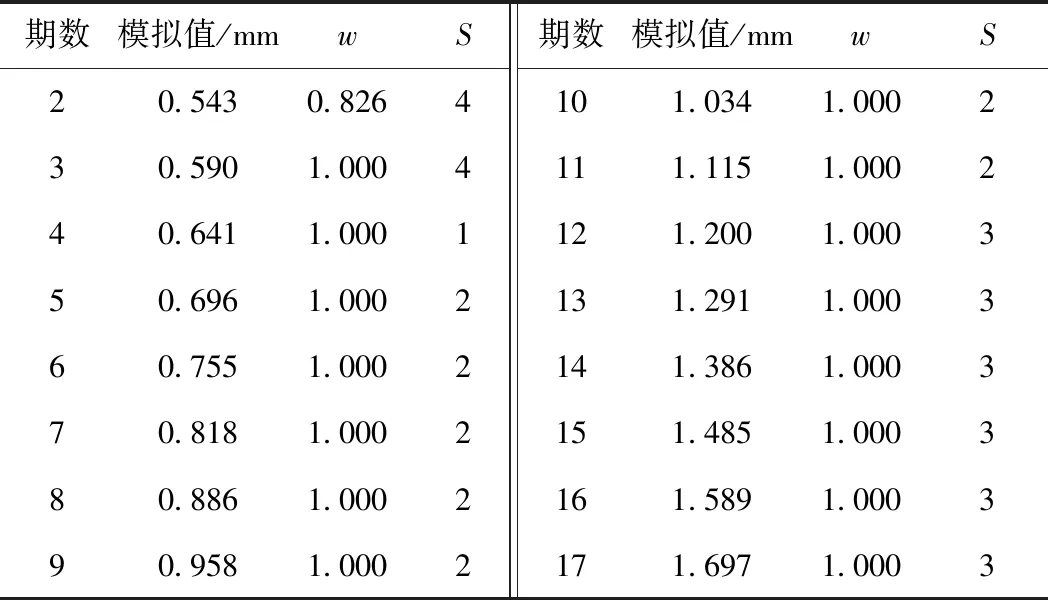
表8 RLM方法模拟值、权因子和状态划分

根据表8及状态转移概率矩阵可知，17期所处状态为S3，在状态转移概率矩阵中S3最有可能一步转移到S3，其概率为1。根据式( 9 )通过状态S3所对应的相对误差修正第18期预测值，同理依次可得后续预测值，各方法模拟值的残差绝对值见图3。接着对预测值状态进行预测，并修正预测值，各方法的预测结果见表9，预测精度指标见表10。

图3 第二组试验各方法模拟值残差绝对值

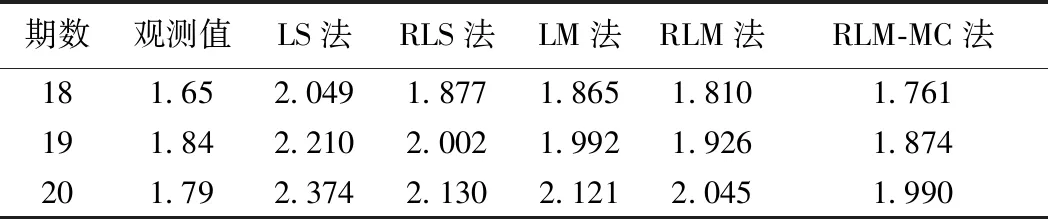
表9 第二组试验各方法预测值 mm

表10 第二组试验各方法预测精度指标

从图3、表9、表10可知，LS法在第二组试验中预测结果偏离实际观测值，且预测时间越长误差越大，第20期预测值误差最为严重，其相对误差为32.626%。而在引入稳健估计后，RLS法的预测精度得到了较为明显的提高，其第20期预测值相对误差下降到18.994%。LM法与RLS法预测结果相近，精度略优于RLS法，在引入稳健估计和马尔可夫模型修正预测值后，RLM-MC法第20期预测值相对误差为11.173%，本文所提方法在第二组观测数据中同样体现出显著的稳健性与准确性。

分析表6、表10可得，在第二组观测数据中，各方法的MAPE均大于表6中相应的值。显然，由于异常值的扰动，各方法的预测准确性都相对有所降低，体现出引入稳健估计的必要性。RLS法引入稳健估计后，精度得到显著提升，RMSE减少了44.902%，证明RLS法有效削弱了异常值对预测结果的负面影响。LM法预测精度略好于RLS方法，进一步表明采用非线性最小二乘参数估计的合理性，且LM法在引入稳健估计与马尔可夫模型后，RLM-MC法的RMSE相对LS法减少了71.150%，证明本文所提方法在高速铁路桥墩沉降预测中的有效性和准确性。

4 结论

本文在分析高速铁路桥墩沉降规律以及实际工程需求后，提出了一种基于RLM-MC的高速铁路桥墩沉降曲线预测方法，并对该方法的预测效果进行了工程实例分析和评估，主要结论如下：

(1)RLM法在两组试验中均能有效提升曲线拟合精度。在第一组试验中RLM法单位权方差相对LS法、RLS法和LM方法分别减少了54.545%、47.368%和51.220%。在第二组试验中，RLM方法单位权方差相对LS法、RLS法和LM法分别减少了51.163%、30.000%和40.000%。这一结果表明RLM方法的参数估计精度明显优于其他三种方法。

(2)结合马尔可夫模型能够更加准确地描述高速铁路桥墩沉降规律，提高预测精度。在两组试验中，RLM-MC方法的MAE、RMSE和MAPE均明显小于其他四种方法，表明本文提出方法在高速铁路桥墩沉降预测中更为准确。