强降雨工况尾矿库堆排坝体稳定性分析

于浩泽 高义军 郭奇峰 刘文胜 潘继良 张文飞

(1.北京科技大学土木与资源工程学院,北京 100083;2.安徽马钢矿业资源集团南山矿业有限公司,安徽 马鞍山 243000)

金属矿石经过破碎、细化、分选和提取所遗留的废弃物称为尾矿,因尾砂粒径小、强度低及透水性差,易受雨水影响而产生滑坡[1];矿石在开采过程中也会剥离出大量废土,这些废土往往堆积于排土场中形成高势能人工松散堆垫[2],同尾矿库一样存在着极高的危险性。这两者的管理、监测和维护,每年都会对矿山企业造成很大的经济压力。近年来,我国对于强降雨及其他极端天气情况下尾矿库稳定性要求有了进一步提升,如果通过设计优化采用废石土堆排尾矿库坝体,则能够在确保尾矿库坝体处于极端天气情况下的安全性和稳定性的同时,还能够实现废石土的排放,为矿山企业带来较大的经济效益。

为满足矿山安全性和经济性要求,国内外许多学者对尾矿库坡面堆排开展了相关研究[3-6]:唐飞[7]首次总结大量工程实践所创造的尾矿库与废石土联合堆排经验,并提出尾矿库上方建排土场坡面堆排技术;穆贵清等[8]通过模拟实验的方式发现坡面堆排工程中底部用以排渗的石块层效果较差时,会导致堆排体内部含水量增大,严重时甚至会造成溃坝;王晓民等[9]分析了不同堆排方式对坝体的安全稳定性的影响,提出了自外向内、自下而上包裹式分层堆排的安全施工方案;朱远乐等[10]在坡面堆排设计中考虑了地震荷载,通过调整边坡脚以及设置工作平面对方案进行了优化。

本研究从降雨和堆排对尾矿库坝体稳定性的影响出发,在ABAQUS 模拟软件中对已有的4种堆排方案进行强度折减计算安全系数,兼顾经济效益优化堆排方案,然后根据凹山尾矿库特定工程背景模拟强降雨条件下凹山尾矿库坝体稳定性,研究结果可以为企业尾矿库坝堆排改造与建设提供合理的参考依据。

1 尾矿库工程概况

凹山尾矿库地处安徽马鞍山市向山镇西南上南庄村境内,原始地形位于两低山丘陵凹地之间,凹山库区内最低高程+15.50 m。该库采用上游法施工工艺筑坝,设计坝高99.5 m(标高+115 m),库容8 863万m3,尾矿库等级为三等。自尾矿库投入运营以来,存在着不同程度的安全隐患问题,虽然矿山企业相继采取工程防范措施,但鉴于尾矿库的特殊性,极端自然灾害导致溃坝时将对当地居民及矿山企业造成重大人员伤亡及财产损失。

库区所在地降雨季节为5—8月,春末夏初为梅雨期,多阴雨天气,降雨量约占全年的1/3,年平均降雨量1 100 mm,年内日最大降水量为107 mm,4—8月份为防洪季节。库区周围没有大的地表水系,地下水以大气降水补给为主,因库区地形复杂不利于地下水集聚,故排渗较好,主要经尾矿库排到下游沟渠。

尾矿库采用上游法筑坝,后期子坝由尾砂堆积而成,子坝外坡比为1 ∶2.5,内坡比为1 ∶2.5,外坡总坡比为1 ∶5.0,尾矿库原坝体侧视图见图1。

图1 尾矿库侧视图Fig.1 Side view of tailings pond

2 堆排方案优选

堆排方案设计应充分考虑设计库容和施工难度,并防止尾矿库原坝堆排过多发生整体剪切破坏,设计方案安全系数应满足《GB 50863—2013 尾矿设施设计规范》的要求。凹山尾矿库是三等库,按照《GB 50863—2013 尾矿设施设计规范》第4.4.1条的要求,堆排后的坝坡在正常工况下坝坡安全系数应该大于或等于1.20。

2.1 堆排稳定性评价理论

根据施工工艺及矿区库存要求的不同,目前已有4个堆排方案,下文中将以强度折减法为标准对各个方案进行稳定性评价。

有限元强度折减法是一种可广泛应用于评价边坡稳定性的数值分析方法,其是在强度折减弹塑性法和弹塑性有限元法的基础之上发展起来的。1975年,Zienkiewicz 等在《土工程弹塑性有限元数值分析》论文中最先提出了强度折减法。强度折减法要求在适当的标准下按系数对抗剪强度进行折减,求得在稳定性临界点时的抗剪强度折减系数。由此对结构的稳定性进行分析所得到的达到临界状态时的抗剪强度折减系数在传统意义上即为Bishop 在极限平衡法中给出的边坡整体稳定性安全系数[11]。强度折减法也可以与渗流—应力耦合来计算降雨条件下边坡的稳定性安全系数,如蔡亚飞等[12]就在ABAQUS中建立了边坡的物理模型,并应用强度折减法和渗流—应力耦合理论,模拟出降雨条件下边坡的应力场、位移场、渗流场以及安全系数。

根据强度折减法理论,土体的抗剪强度参数可分别表示为

式中,c、φ为土体所能提供的抗剪强度参数;cm、φm为维持平衡所需要的或土体实际发挥的抗剪强度参数;Fs为强度折减系数。

利用ABAQUS 可获得折减过程塑性应变历程及范围,从而从整体上综合评价边坡稳定性。在ABAQUS 中,可以将材料特定参数设置为预设场的函数,通过逐步降低预设场的值从而使土体逼近稳定性临界点,达到强度折减法求安全系数的目的。

2.2 堆排方案介绍

尾矿库堆排方案设计考虑的主要指标为安全稳定性、库区容量和施工难度,根据不同侧重点设计有4个方案:基础全换填、基础清除局部素填土、基础局部碎石桩加固、基础不处理。4个方案的剖面示意见图2。

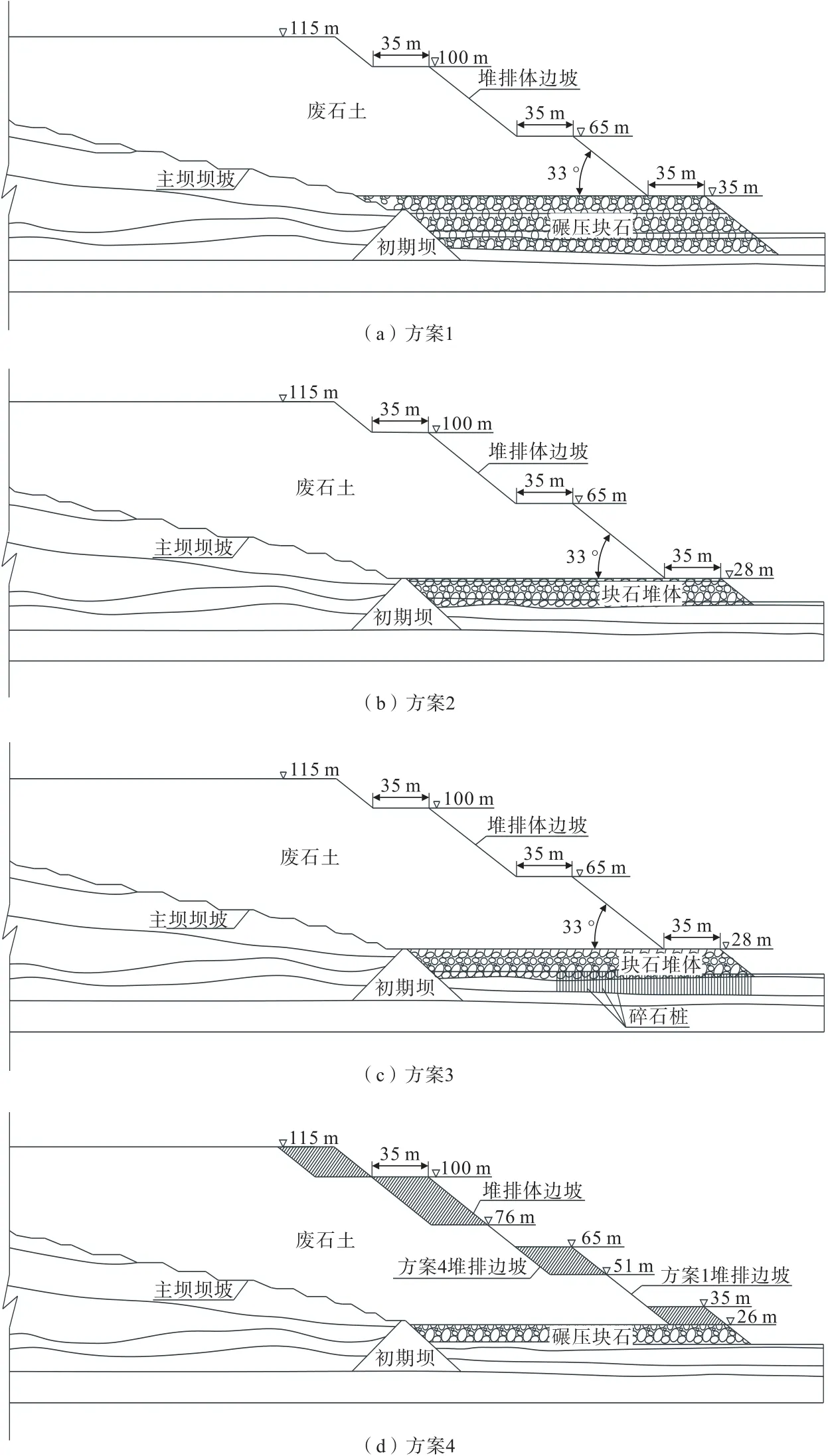
图2 4个方案剖面图Fig.2 4 schemes section diagram

(1)方案1,基础全换填(表层素填土和粉质黏土全部清除)。在此方案中应将天然基础软土层大部分去除,改用力学性质优良的岩石材料换填以作为持力层,可以有效地提高基础的承载能力并减少基础的沉降量。

(2)方案2,基础清除局部素填土。基础表层的素填土与粉质黏土一并去除。通过稳定计算分析得出主坝压坡体第一级台阶高度对于不同基础处理方案边坡稳定有很大影响,所以本方案考虑在基础处理前对主坝压坡体内第一级台阶高度进行调整,即把原方案第一级台阶标高+35 m 调整到+28 m,其余台阶高度及台阶边坡角均未调整。

(3)方案3,基础局部碎石桩加固。为了减小工程量,主坝压坡体第一级台阶调至+28 m,然后做基础处理。根据稳定计算的最危险滑弧,考虑从滑出面区域对基础进行局部碎石桩处理,即仅在邻近压坡体坡脚120 m 以内采用碎石桩加固,碎石桩处理平面面积约4.8 万m2。根据稳定性计算,要求压坡体+28 m标高平台以下范围均采用块石堆体。

(4)方案4,基础不处理。基础不处理的情况下,对典型剖面不同的第一台阶高度分别进行稳定性分析计算。

2.3 堆排方案优选

经强度折减得到的各种方案的危险塑性断裂带(安全系数)见图3。PEMAG(塑性应变)衡量塑性变形程度,当期大于0.01 时可认为有较大的永久变形产生,即云图中灰白色及以上区域都产生了危险的塑性变形。根据稳定性分析结果,4个方案安全系数均高于规范值,且均具有一定安全裕度。从云图得到的断裂带位置来看,方案1、方案4为坡顶至第一级台阶坡脚处,贯穿了堆排体的每一级台阶,滑坡体较大,约210 万m3;方案2与方案3为坡顶至第二级台阶坡脚的弧形带,滑坡体约190 万m3。

图3 设计方案与安全系数对比Fig.3 Comparison of design scheme and safety factor

方案1 至方案4 在设计库容,施工难度和施工周期上各有侧重,对各种方案优缺点的详细分析见表1。

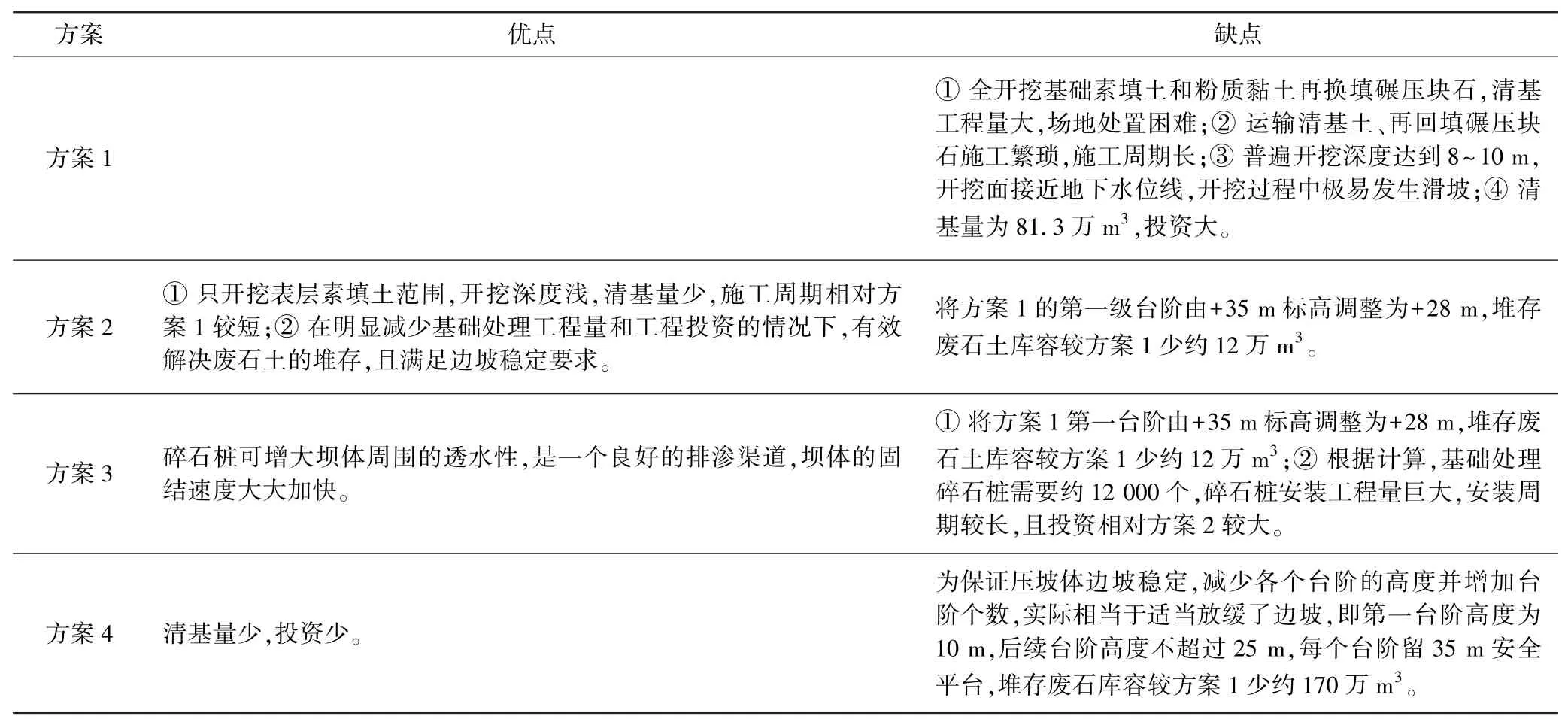
表1 方案优缺点对比Table 1 Comparison of the advantages and disadvantages of the schemes

综合稳定性分析与方案投资比较,方案2 在满足最小安全系数的前提下,清基工程量最少,施工周期最短,工程投资也相对较少,且能有效解决原方案废石土的堆存,于是选择方案2为基础进行进一步的渗流分析。

3 强降雨条件下坝体渗流分析

3.1 降雨入渗理论

根据非饱和土力学理论,当降雨条件发生时,边坡的非饱和入渗场会发生如下变化:首先,随着雨水不断入渗坡体,边坡上部的非饱和区含水量会不断增加,基质吸力会不断降低。其次,基质吸力的降低又会使非饱和土体的黏聚力减小。根据摩尔—库仑抗剪强度准则,构成边坡的土体的抗剪强度也会降低,这会显著降低边坡的稳定性[13]。

边坡降雨入渗问题是一个非饱和土体渗流问题,在ABAQUS 中渗透系数由饱和度决定,而饱和度又与基质吸力相关,所以对于任何土壤条件,都存在着一条限制土壤“入渗能力”的临界曲线。任何时刻,一旦降雨强度超过了入渗能力临界曲线,多余的雨水将不再入渗,转而形成地表径流。

降雨入渗是一个十分复杂的过程,Mein 和Larson 首先采用了土壤允许入渗的容量fp、曾采用降雨强度q、土填饱和时的水力传导系数Kws这3个因子描述土壤降雨入渗全过程中可能出现的不同现象[14]:q＜Kws时,降雨全部入渗,地表不会产生径流,入渗率保持不变;fp＞q＞Kws时,降雨全部入渗,地表不会产生径流,fp随着入渗深度的增加而变小,但此时降雨强度还未达到土壤允许入渗的容量,此时坡面为流量边界;q＞fp时,降雨强度大于土壤的入渗容量,部分降雨并不入渗而形成地表径流,土体处于饱和状态。

以上做法只是对于入渗边界条件的一个抽象描述,在ABAQUS 中可以针对不同类型的入渗边界条件做详细设定[15]:

(1)定义与孔压相关的孔隙流动。在计算中,孔隙流体流速可以作为孔压的函数,有以下关系:

式中,vn为边界法线方向的流速;ks为渗流系数;uw为边界上的孔隙水压力;为参考孔压。此式可以很好地模拟基质吸力的提升所引起的渗流速度降低。

(2)定义自由渗出段边界。该种边界只允许孔隙流体流速沿法向向外,即只允许流体输出不允许输入,此时假设土体表面上的孔压为正时,孔隙流体流速与孔压成正比;孔压为负时,流速为0。案例模型中,坡角处水平面为此类边界。

(3)直接定义渗流速度。渗流速度分为表面孔隙渗流速度和集中孔隙渗流速度,将其按载荷看待时,分别对应于面载荷和集中载荷。案例模型为二维,为平面应变问题,所以采用定义表面孔隙渗流速度的方案,与降水直接接触的坡面为此类边界。

3.2 坝体渗流模拟

降雨入渗会使尾矿库坝体内部的含水率上升,而含水率的上升又会使坝体内孔隙水压力发生变化。在天然状态下,地下水位线(浸润线)分隔开饱和区与非饱和区,饱和区中孔隙水压力为正,非饱和区中孔隙水压力为负,负孔压越小,其基质吸力就越大。降雨入渗的实质即是影响非饱和区的土体,使其孔隙水压力趋向于0,在此过程中非饱和区土体的基质吸力逐渐降低,抗剪强度逐步减弱。

考虑到库区地区历史最大日降雨量为107 mm,于是本次模拟将110 mm/d 作为强降雨强度,0～72 h降雨过程中原坝体与堆排坝体的孔隙水压力的分布情况分别见图4、图5。

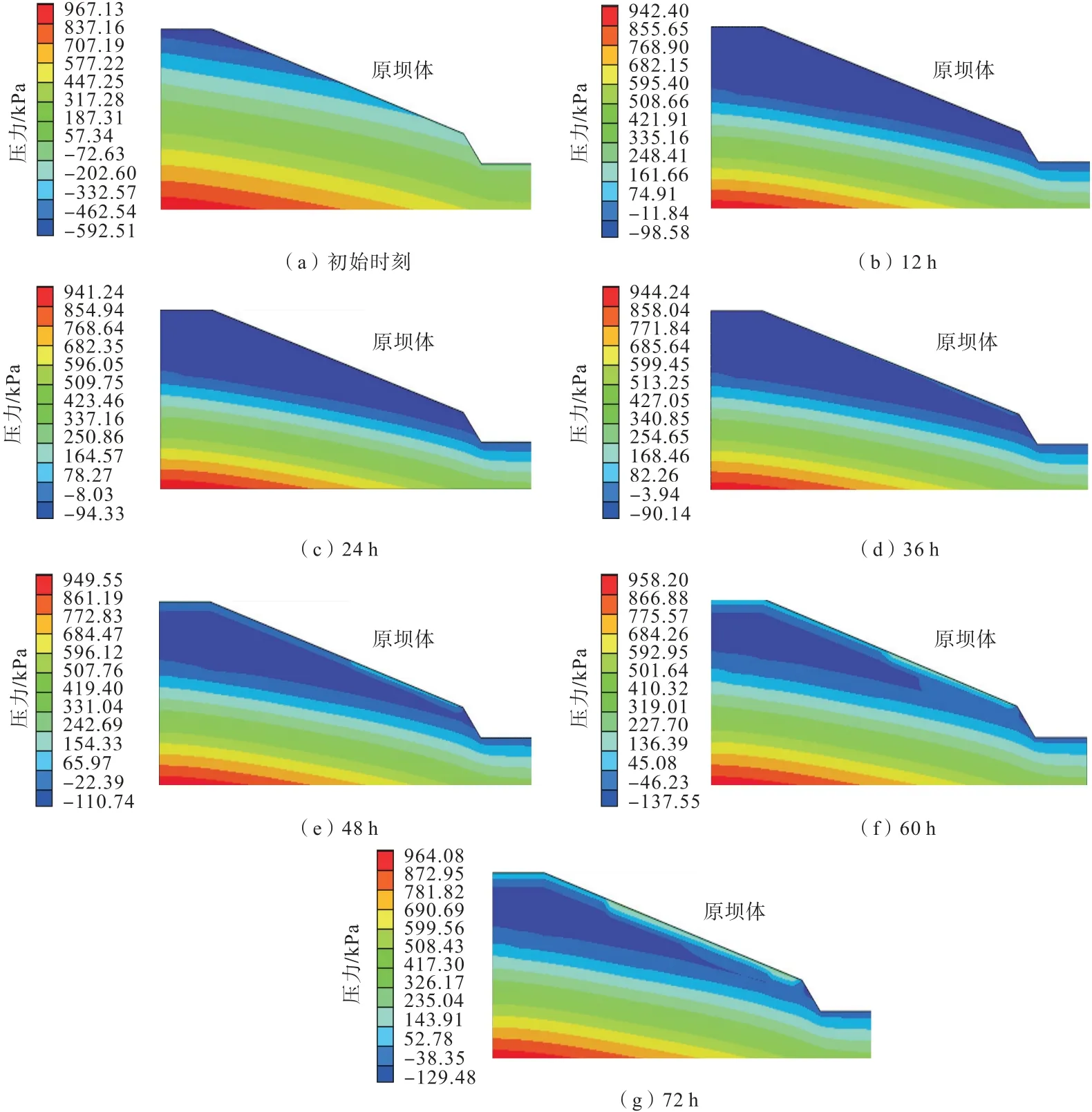
图4 原坝体不同时刻孔隙水压力分布图Fig.4 Distribution map of pore water pressure of the original dam at different times

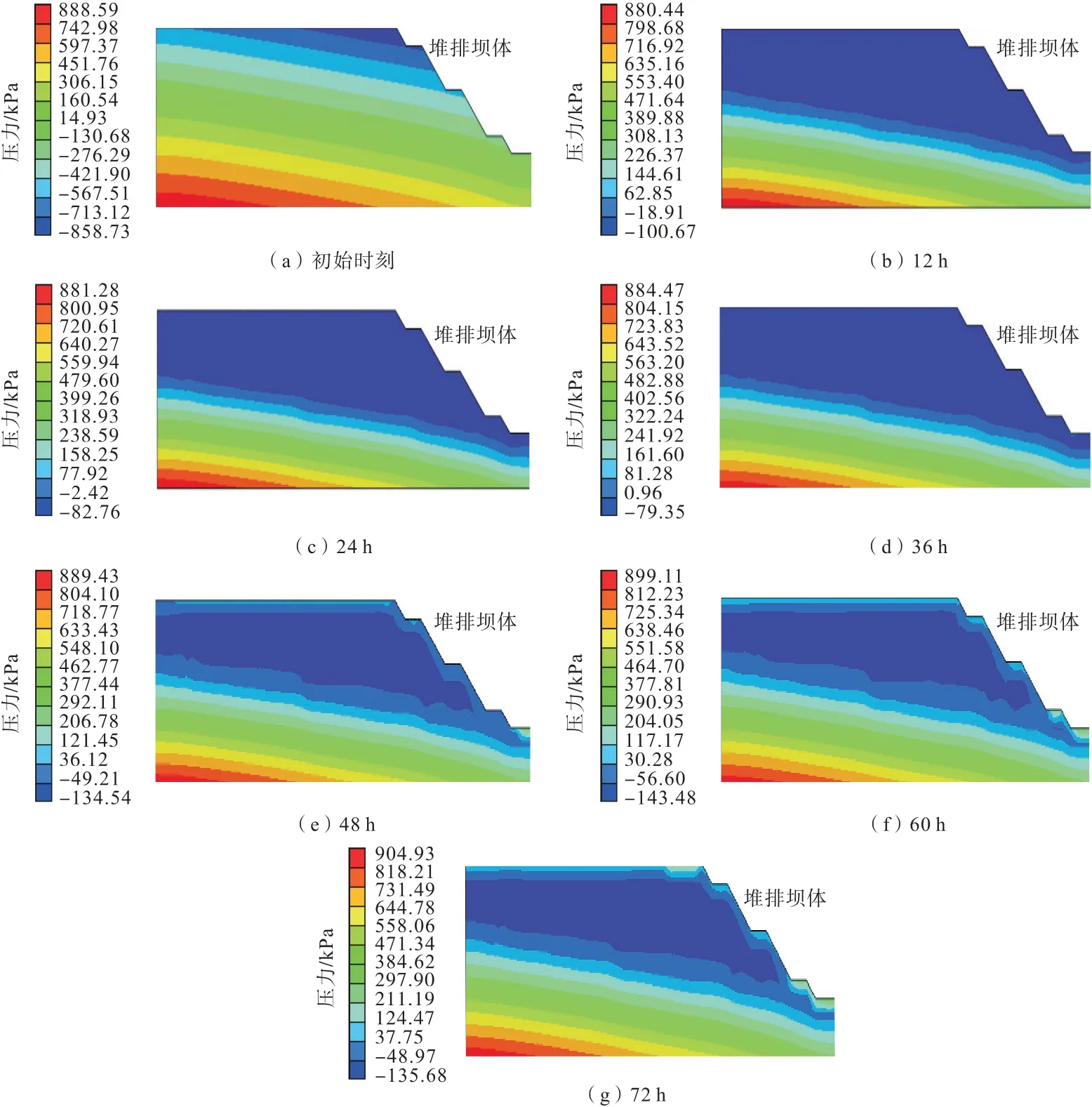
图5 堆排坝体不同时刻孔隙水压力分布图Fig.5 Distribution map of pore water pressure of stack-drainage dam at different times

在初始状态下,可以看到2个坝体包括基质吸力在内的孔压仍然呈现线性分布,坝体坡脚处为自由排水面,坝体内部地下水位位置符合地质勘探结果,2个坝体孔压符合初始条件,原坝体顶部孔压为-592.51 kPa,堆排坝体顶部为-858.73 kPa。降雨12 h 原坝体与堆排坝体水位线以上大部分区域孔压有大幅抬升,说明正处于q＜Kws阶段,雨水下渗速度较大,但一直到36 h,2个坝体都处在fp＞q＞Kws阶段,造成孔压分布变化不明显。到降雨48 h,原坝体率先于堆排坝体到达q＞fp阶段,反映在孔压分布图上则是原坝体坡脚处首先出现了正的孔压力,而堆排坝体的下渗深度要比原坝体大,原因在于原坝体之上的尾砂较细碎,其透水性要比堆排体中的废石土差得多。直到72 h 降雨停止2个坝体的降雨入渗深度都未发生大的变化,只有正孔压范围都从坡脚向坡顶蔓延,原因是坡体下部受降雨入渗和坝体上部水分下渗的双重影响,使坝体下部总是要比上部更快达到饱和。最终由于饱和度的提高,孔隙水压力增大,基质吸力逐渐减小,雨水的下渗速度放缓,加之降雨强度逐渐减小,可看到2个坝体的入渗深度停留在差不多的位置,但原坝体由于更低的渗透性,其表面附近积累了比堆排坝体更大的孔隙水压力。

总体上看原坝体与堆排坝体在降雨的全过程中虽然有着相似的变化过程,但就某一点在2个坝体中的表现来说不能一概而论,而这也正是堆排对尾矿库坝体产生影响的关键,特征点的孔隙水压力变化情况见图6。

图6 特征点孔隙水压力变化图Fig.6 Variation map of pore water pressure at characteristic points

初始状态下坡顶、坡中以及坡脚的孔隙水压力并不相同,但降雨发生12 h 后,3 处的孔压都来到了-50 kPa 附近。此后坡脚的孔压平稳增长,坡中与坡顶的孔压以略低于坡顶的速度增加。在降雨后期,坡中的孔压突然增大到与坡脚齐平,与上述分析中的土体基质吸力降低造成雨水下渗不畅在坡中部大量聚集的结论相吻合。而坡顶由于长时间的降雨,吸力降低在60 h 就已不再大幅增长,即q＞fp,后续的降雨多以地表径流的形式向坝体下方传递。反观堆排坝体,坡脚位置由于顶部覆土的存在,大大拉长了其与自由排水面和坡面的距离,受降雨影响小,孔压主要受地下水位的影响。所以从100 kPa 开始以极小的速率缓慢增加,坡中与坡顶的孔压在降雨开始12 h 后增大到-100 kPa 后保持平稳,36～72 h 期间坡顶与坡中孔隙水压力发生交叉。分析其原因在于不同深度土体的渗透性不同:36 h 时,坡面首先达到饱和,相当于一个短暂的不透水层,但坡顶区域的雨水依然在下渗,这就在坡顶区域内形成了一个负压区,使坡顶孔压小于坡中,当雨水继续下渗,不透水层来到了坡顶,坡中就形成了负压区,使得坡顶与坡中孔压实现交叉。对比原坝体与堆排坝体特征点孔压图,在堆排的保护下,特征点孔压不存在持续增长的趋势,且孔压一直保持在0 kPa 以下,说明堆排可以很好地遏制孔压的增长,间接地为坝体提供了安全运行所需的抗剪强度。

4 强降雨条件下坝体稳定性分析

4.1 位移分析

基于上述的孔隙水压力的分析,再进一步叠加进坝体在强降雨工况下位移的发展情况,来讨论坝体的稳定性变化趋势。0～72 h 坝体水平位移以及竖直沉降分布如图7、图8所示。

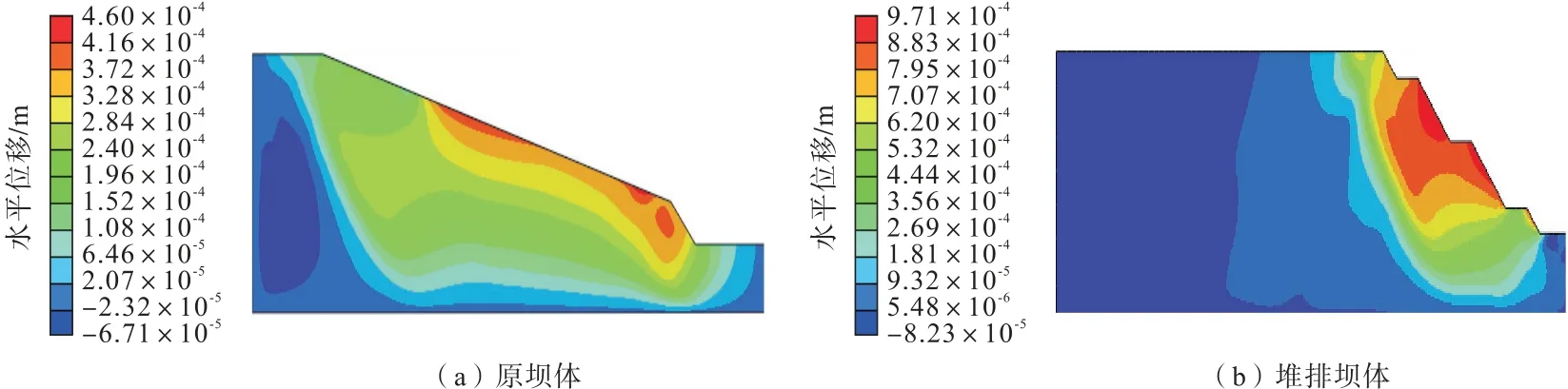
图7 水平位移分布图Fig.7 Horizontal displacement distribution map

图8 沉降分布图Fig.8 Subsidence distribution map

原坝体水平位移主要发生在沿坡顶到坡脚的弓形区域,与危险滑动面基本一致,最大水平位移发生在上部坡面处。堆排坝体水平位移发生在沿坡顶到第二级台阶坡脚的弓形区域,与其自身的危险滑动面也高度重合,最大水平位移在其第三级台阶处,据此可得出水平位移为坝体滑坡变形的主要形式。坝体最大沉降发生在顶部,顶部附近有不明显的对称面,之所以如此是因为降雨入渗后,基质吸力降低,孔隙水压力增加,有效应力减小,坝体顶部依据含水量的差异而不同程度地出现了卸载回弹的现象而后由于容重增加产生了固结;对于坝体底部,后期降雨入渗缓慢,顶部产生固结时,底部才刚刚进入卸载回弹阶段。堆排坝体的最大沉降是发生在第三级台阶处,也就是最大水平位移发生处,反映了这部分坝体向下、向外位移的趋势,更加印证了堆排坝体的不稳定性。

4.2 稳定性分析

使用强度折减法得到0～72 h 坝体安全系数变化情况如图9所示。

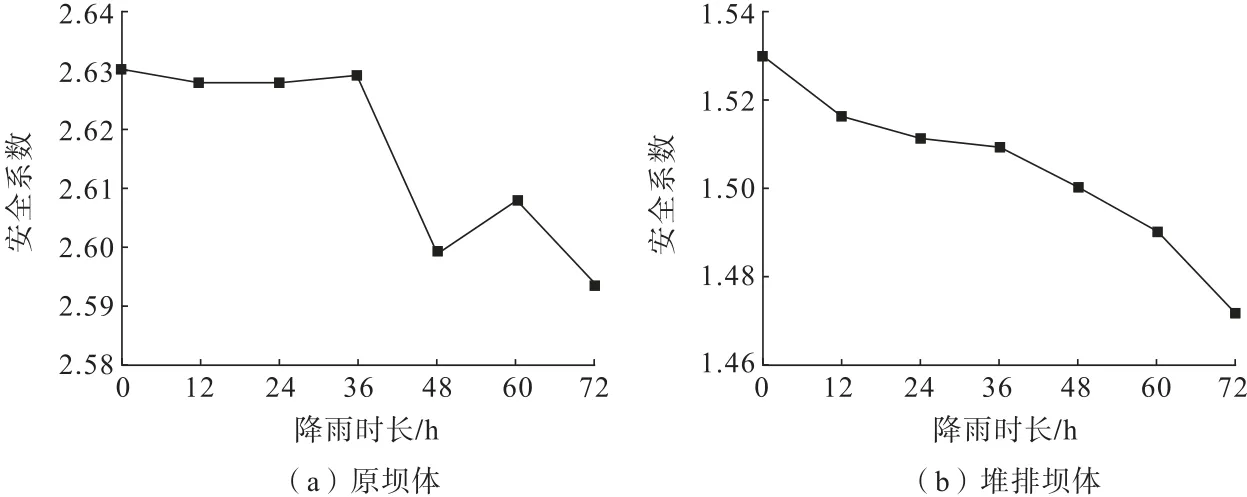
图9 安全系数变化图Fig.9 Safety factor change chart

降雨36 h 前原坝体安全系数并无明显变化,36 h后突然降低,说明此时危险滑动面因为雨水渗透造成抗剪强度降低,但是48 h 以后表层土体进入q＞fp,下渗的雨水变少,地表形成大量径流,断裂带土体也达到了最佳含水率附近,产生了固结的效果,安全系数也得到了回升,60 h 后已经入渗的雨水继续下渗,土体容重的增大与抗剪强度降低范围的增大已远远超过了固结的影响范围,安全系数出现了进一步的降低。堆排坝体则是从降雨一开始安全系数即降低,堆排坝体危险滑动面相对不固定,每级台阶都有可能发生失稳,在36 h 附近坝体因固结作用的影响安全系数降低的趋势有所减弱,但总体仍呈一次函数形式稳定降低。总体上看,坝体安全系数在降雨发生后即稳步降低,堆排后安全系数下降很多,但根据上述分析可知,危险滑动面仅存在于堆排体内部,所以安全系数的降低并不是由于堆排体把原坝体压坏导致的,不稳定因素全部出现在堆排体内部。

5 结 论

以凹山尾矿库为研究对象,基于现场勘测得到的数据,对已有的4个坡面堆排方案应用强度折减法进行了安全稳定性模拟,并针对基础清除局部素填土方案建立了强降雨工况下的二维渗流模型,对渗流场和稳定性变化特征进行了分析。

(1)基于已有的基础全换填、基础清除局部素填土、基础局部碎石桩加固以及基础不处理4种堆排方案建立了二维数值模型,运用强度折减法对各方案的安全稳定性以及施工难度、经济效益进行了初步评价。结果显示4个方案均满足最小安全系数要求,因方案2 具有施工难度低、库容大的优势,最终选择了方案2 基础清除局部素填土为最优堆排方案。

(2)基于饱和—非饱和渗流理论及降雨入渗理论分析发现降雨入渗对堆排坝体坡顶、坡中及坡脚的影响不同。因为降雨入渗速率与基质吸力有关,导致了不同深度土体的渗流速度有差异,进一步发现了负压层的存在,并且因为负压层,孔压不再随深度成线性变化,降雨约60 h 后,坡顶与坡中对于降雨敏感程度将迎来变化,而坡脚处对于降雨的敏感程度一直较低,坝体堆排之后更是几乎不变。

(3)堆排对原坝体的孔压起到了保护作用,但安全系数却在堆排后大幅降低,说明堆排将塑性不稳定滑动面转移至堆排体内部。堆排后坝体安全系数在降雨发生后呈现稳定下降的形式,这是由降雨入渗基质吸力降低导致的抗剪强度降低以及土体到达最佳含水率而发生固结导致的抗剪强度提升两方面因素引起。