朗肯土压力理论在露天边坡设计中的应用

郭献章 李凤柱 秦嗣龙 张娟霞 杨治华 郑立志 张学芝

(1.东北大学秦皇岛分校实验教育中心,河北 秦皇岛 066004;2.北方燕盛工程技术有限公司,河北 秦皇岛 066000;3.河北钢铁集团矿业有限公司庙沟铁矿,河北 秦皇岛 066000;4.东北大学秦皇岛分校资源与材料学院,河北 秦皇岛 066004;5.东北大学秦皇岛分校发展规划处,河北 秦皇岛 066004)

边坡角关系着露天开采的安全与效益,历来受到理论研究与工程技术界的重视,即在经济合理的基础上保证边坡的稳定。边坡角的经济技术可靠性来源于以下四个方面:① 是否找到了最危险滑面;② 是否提供了可靠的强度参数;③ 是否确定了合理的工况(即荷载组合方案);④ 计算方法本身的合理性[1]。针对以上问题,无论是传统的极限平衡法,还是现在基于高性能计算的数值方法,都因边坡的复杂性而不能很好地解决。此外,经验类比法、神经网络法、模糊数学法等边坡稳定的分析法,也大都基于工程经验,根据剥采比、开采深度、矿石品位等经济技术指标来确定边坡角的大小,其结果往往偏于保守[2-4]。因此在实施中,关于边坡角的设计,还存在有较大的分歧,还需要借助现场的经验介入。

朗肯土压力理论是现代土力学两个著名的古典土压力理论之一,是英国学者朗肯(Rankine W J,1857)在半无限弹性土体处于极限平衡应力状态假定基础上所得出的结论[5]。由于其概念明确,方法简单,至今仍被广泛使用,特别是在各种地基承载力计算中,已经被列入国标规范[6]。受朗肯土压力极限平衡角(45°±φ/2)的启示,发现在此角(45°±φ/2)与自然安息角φ所形成的角度区间内留设边坡角,边坡稳定状态对岩土坡体的内聚力要求很小。这就为弱内聚力的坡体边坡角设计及坡面支护提供了有益的思路与指导。通过对露天矿边坡角、坡高与坡体的内聚力c、内摩擦角φ之间的关系进行了研究,并结合北方燕盛工程技术有限公司多年的施工经验总结,基于朗肯土压力公式与莫尔圆理论,得出些许有益认识,供工程技术同行参考讨论。

1 理论基础与研究模型

根据材料力学单元体的受力状态(如图1(a)),在不考虑中间主应力σ2的情况下,可以得到如图1(b)所示的莫尔圆,应力关系式[7]如下:

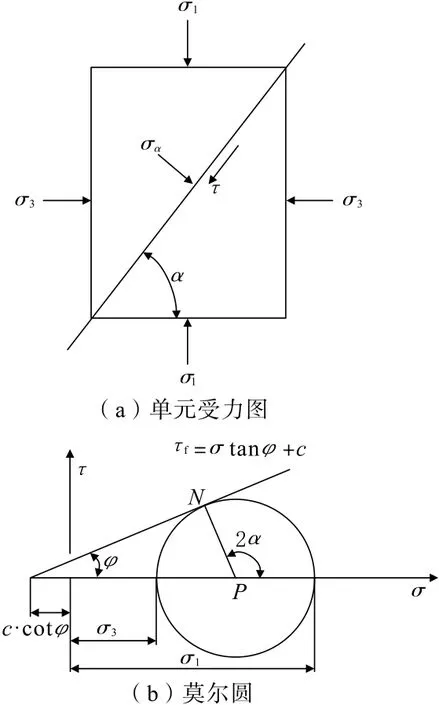
图1 单元受力图及莫尔圆Fig.1 Diagram of force on unit and its Mohr's circle

在极限平衡状态时,可以得到如下主应力与切应力的关系:

式中,σ1、σ3分别为最大、最小主应力;σ为任意截面上的正应力;τ为任意截面上的切应力;τf为极限状态时的切应力;α为所研究截面与最大主应力的法平面之间的夹角;φ为边坡土体的内摩擦角;c为边坡土体的内聚力;γ为岩土体的重度;z为单元体的埋深。

由上式可知,实际破裂面和最大主应力作用面夹角分别呈(45°+φ/2)和(135°-φ/2)。

朗肯土压力原理如2(a)所示,当挡土墙OEE′O′在土体的作用下向左偏斜至ODD′O′时重新达到平衡,左侧土体受到挤压,为被动土,其极限平衡面为OB,水平方向的主应力为最大主应力(σx=σ1),极限平衡角为(45°-φ/2)。在墙体右侧,是主动土,其极限平衡面为O′F,竖直方向的主应力为最大主应力(σz=σ1),极限平衡角为(45°+φ/2)。以上原理的莫尔圆图解如图2(b)所示。

根据朗肯土压力理论,其主动土压力范围的临界线倾角为αf=(45°+φ/2),这个角度的平面上方的土体△O′FD是不稳定的;处于自然安息角平面下方的土体△O′FG是稳定的。

如图2(c)所示对于边坡来说,边坡体相当于主动土,O′G右下侧部分的土体不会出现失稳。但这个角度对于露天矿边坡来说,虽安全但不经济,矿山总是在安全条件下追求最大的边坡角。那么处于△O′GF这个区间的土体的稳定性如何,把α=(45°+φ/2)做为边坡角时需要满足什么条件,有什么优势,值得进一步探讨。实践证明,这个区间内的土体如果自稳,是必须要求有一定的内聚力的,也就是说不能是理想的非粘性土。不过在自然界中,理想的非粘性土存在的情况很少,即便是风成的沙丘,在一定的含水率下也有相当程度的内聚力,而这个量级很小的内聚力就足以维持一定深度的直立壁的开挖,可见在△O′GF区域内自稳所需的内聚力很小,所以称之为“工程友好三角区”。为研究一定内聚力参与下△O′FG区域内的土体稳定性问题,应用极限平衡原理,进行了如下系列的计算与验证。

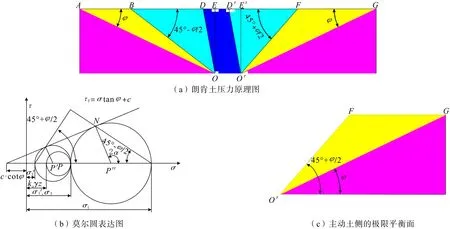
图2 朗肯土压力原理及其摩尔圆表达图Fig.2 Schematic diagram of Rankine's theory of earth pressure and diagram of its Mohr's circle expression

2 “工程友好三角区△O'FG”区域自稳计算

建立边坡计算模型,边坡角αf=(45°+φ/2),求解使边坡处于极限稳定状态所需的内聚力,此时边坡的安全系数为1.0。采用瑞典滑弧理论[8],运用北京理正软件股份有限公司的边坡稳定性计算软件,不考虑地下水的影响,进行分析。求解模型及计算公式如图3 和式(4)。

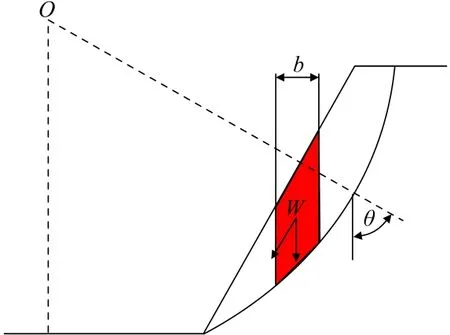
图3 求解模型Fig.3 Solving model

式中,K为整个滑体剩余下滑力计算的安全系数;l为单个土条的滑动面长度,m,l=bsecθ;b为单个土条的水平宽度,m;W为条块重力,kN,浸润线以上取重度,以下取饱和重度;θ为条块的重力线与通过此条块底面中点半径之间的夹角,(°);c、φ为土体抗剪强度指标,此处取总应力指标。

坡内土体按同一岩性考虑,重度γ=18.5 kN/m3,坡高分别取12、15、30 和50 m,土体内摩擦角φ分别取20°、25°、30°、35°、40°和45°,坡体的边坡角取αf=(45°+φ/2),反算使边坡处于极限平衡状态时的内聚力。

3 计算结果分析

3.1 αf=(45°+φ/2)时所需的内聚力

在极限平衡状态下,安全系数K=1 时,所需内聚力计算结果见图4。从图4 可知,不管边坡角是什么数值,不管边坡高度多大,在采用αf=(45°+φ/2)的边坡角时,如果内聚力为零,边坡都是不稳定的,都需要一定的内聚力才会使边坡处于临界稳定状态。实际上,这个基于朗肯土压力的极限平衡面O′F(如图2所示),是在全部力的共同作用下的优势破裂面,也即在此面将会产生最大的剪应力。假如以此面为界把其左上侧的作用力去掉,则合应力在此面不再平衡,相当于作用在此面的法向正压力减小为零,如果以此面形成边坡面,则必定会失稳滑坡。

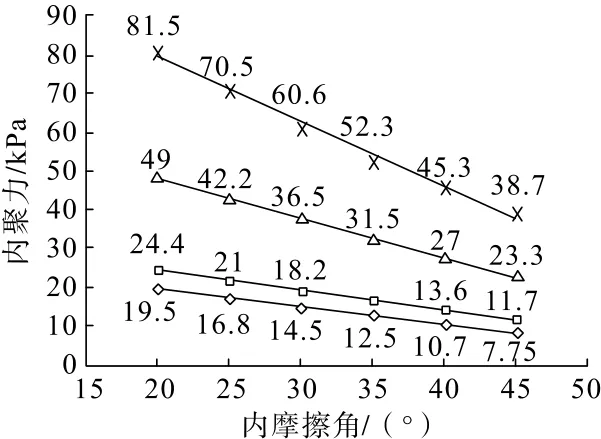
图4 边坡角为αf=(45°+φ/2)时,内聚力—内摩擦角关系Fig.4 The relationship between cohesion and angle of internal friction when slope angle αf= (45°+φ/2)

边坡岩土体都会有大小不同的内聚力存在的,因此随着内聚力大小的不同,在此边坡角边坡的内部会形成距坡面深浅不同的一个极限平衡面,也就是潜在的滑移面。如果组成边坡的物质是理想散体,理论上内聚力为零,则这个面与水平面的夹角应该是该物质的自然安息角[9],也就是O′F重合于O′G(如图2)。通过分析O′F与O′G面之间的边坡角与内聚力、内摩擦角、坡高的组合,能够很好地计算出临界边坡角,从而优化出最佳边坡角。

由图4 可知:

(1)内摩擦角越大,利用αf=(45°+φ/2)开挖所形成的边坡需要的内聚力越小,虽说大的内摩擦角对于αf=(45°+φ/2)开挖的边坡有利[10]这一结论是行业共识,但在坡高确定时,c-φ关系的线性曲线拟合的相关度R2≥0.9886,这一近于直线关系,在实践应用中更为便利。比如坡高一定时,可以根据c-φ之间的线性负相关关系,充分利用φ值和c值互补关系,来确定经济合理的边坡角及支护手段。

(2)边坡高度越大,需要的内聚力越大,才能达到极限平衡状态。

(3)以αf=(45°+φ/2)开挖的边坡,其达到极限平衡所需的内聚力是很小的。在内摩擦角为20°时,仅需19.5 kPa。在内摩擦角为45°时,仅需7.75 kPa。这对于比较破碎的边坡的支护给出了重要的启示,比如在坡高、边坡角、内摩擦角一定时,如果边坡达不到安全系数要求,则边坡可以放缓到(45°+φ/2,φ)的区间内,但需要一定的支护工作,增加一定的内聚力。而这个量级不大的内聚力要求,可以用土钉[11]、土锚杆[12]等低成本的工程来实现。

3.2 滑坡体厚度

将上述极限状态的滑弧位置,按比例画出,同时标出各滑体的厚度,部分结果详见图5。图中标注的数字说明如下:“1220”表示边坡高为12 m,内摩擦角为20°时的极限滑坡的形状。坡顶上所标数字是滑坡体顶部水平厚度,中间标注的是滑坡体最大厚度,单位均为m。

图5 不同坡高时极限稳定状态的滑坡体Fig.5 Landslide in ultimate stable state at slope of different height

将计算结果中滑坡体的坡顶宽度和厚度进行统计(见表1),为了反映坡高的影响,将坡顶宽度和厚度分别除以坡高,得出其比值分别称为宽/高比、厚/高比。

表1 不同坡高滑弧体顶部水平宽度和最大厚度Table 1 The top horizontal thickness and maximum thickness of sliding arc body with different slope heights

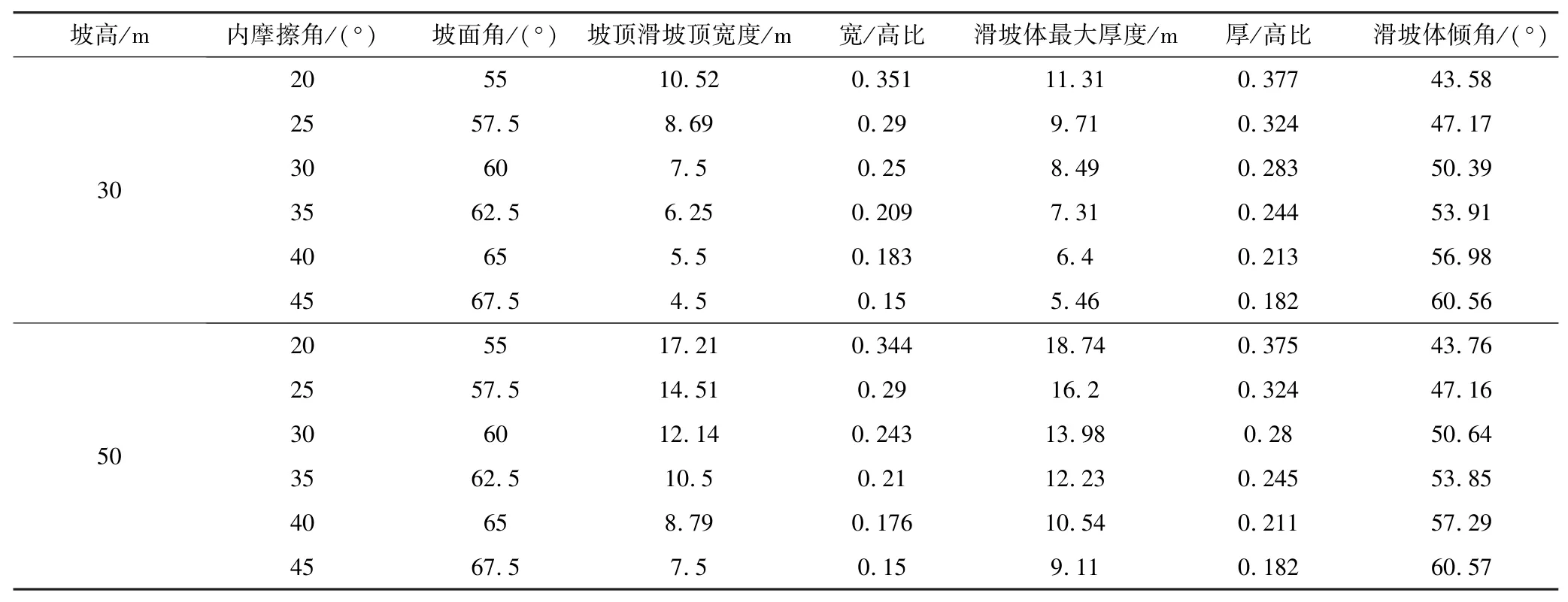
续表1

从表1 可以看出,以αf=(45°+φ/2)形成的边坡,其滑坡厚度(坡顶宽度和滑坡体最大厚度)和坡体高度几乎是标准的线性关系,误差非常小。例如内聚力为25 kPa,边坡角为62.5°时,坡高从12 m 到50 m,其坡顶滑坡宽度和坡高之比最大偏差仅为0.003,最大厚度与坡高之比最大偏差为0.002,几乎完全是一样的。

由图6 厚/高比—内摩擦角关系可知,厚/高比—内摩擦角负线性相关,相关系数R2=0.97,但斜率很小,仅为0.009 5,近于平直线。所以在坡高确定后,滑坡体厚度也基本确定[13],随着内摩擦角的增大,滑坡体的厚高比相应减小,但减小幅度不大。而在内摩擦角确定时,滑坡体的厚度与坡高正直线相关。在工程实践中,为了减少大规模的滑坡发生,不宜强制并段以增加单台阶坡高[14];为了防止厚大滑体的出现,往往用大平台将高边坡从腰部截开,从而减小大应力向下的传递,进而阻断厚大滑坡体的形成。

图6 厚/高比—内摩擦角关系Fig.6 Thickness/height ratio- angle of internal friction diagram

图7 的拟合曲线显示,滑坡体顶部宽度与坡高之比—内摩擦角更近于一条直线,相关系数R2=0.998 5,直线的斜率更小,仅0.007 2。滑坡体顶部宽度与其最大宽度成正比关系,但在实践中前者更便于观察与测量,因此这个指标更好掌握。在已知相关参数的情况下,可以很方便地通过滑坡体顶部宽度来推测滑体的总方量[15],也可以在设计中通过调整坡高来保证安全系数。

图7 滑坡体顶部宽度与坡高之比—内摩擦角关系Fig.7 Relation schema of ratio of slope top width to slope height-internal friction angle

3.3 内聚力和坡高的线性关系

如果按αf=(45°+φ/2)的边坡角形成边坡,当其处于极限平衡状态时,所需的内聚力、内摩擦角与坡高的关系曲线详见图8。

图8 边坡角为αf=(45°+φ/2)处于极限稳定状态时的参数关系Fig.8 Parameter relation diagram of slope in ultimate stable state when slope angle αf= (45°+φ/2)

由图8 可知,当边坡角为αf=(45°+φ/2)时,处于极限稳定状态的c-φ呈线性负相关,相关系数约为0.99,说明在维持边坡稳定的功能上,c、φ两参数可线性互补,当一个值不足时,可以从另一个值入手进行边坡的稳定性设计工作。随着边坡高度的增加,拟合线的斜率也随之增加,直线的截距也在增大,表明维持高大边坡稳定性的坡体材料强度指标c、φ值也必须增大。上述计算还表明,在极限平衡状态下,随着内摩擦角的增大,即使岩土只有较小的内聚力,也可以维持较大的坡面角,从而得到了坡面角—内摩擦角的正相关线性曲线。

图9 内聚力—坡高拟合曲线显示,边坡处于极限状态时坡高和内聚力的线性关系非常突出,相关系数基本上都为1,斜率平均为1.1。此曲线充分说明,边坡土体的内聚力是边坡极限高度的决定因素之一[16],在边坡设计中,内聚力的准确测定与取值,对于边坡高度的设定至关重要。然而边坡的内聚力会在外界因素的介入下发生变化,比如风化弱化,降水入渗等都会严重减小内聚力[17],所以边坡的日常管理中,一定要防止边坡岩体持续严重强度弱化的发生,才能保证边坡的安全。

图9 边坡角为αf=(45°+φ/2)且处于极限稳定状态时所需内聚力和坡高的关系Fig.9 The relationship between cohesion and slope height in ultimate steady state when slope Angle αf=(45°+φ/2)

3.4 滑坡体倾角

在边坡角为αf=(45°+φ/2)且处于极限稳定状态时,可计算得到滑坡体上缘和下缘连线的坡面角和内摩擦角有密切的关系,和边坡高度关系不大。例如当内摩擦角为20°时,滑坡体上缘和下缘连线的坡面角为42.92°～43.76°,相差不到1°。内摩擦角为25°时,坡面角46.99～47.16°,也就是说,坡面高度从12～50 m,滑坡体下缘和上缘连线的坡面角相差不到0.2°,基本上是一致的。

仿朗肯土压力计算公式αf=(x+φ/2)反算x,得出图10。

图10 滑坡体倾角—内摩擦角关系Fig.10 Relationship between angle of landslide mass and angle of internal friction

图10为αf=(x+φ/2)时,滑坡体倾角—内摩擦角关系的线性拟合曲线,图10 显示,滑坡体上缘和下缘连线的滑坡体倾角随内摩擦角变大而变大,但是和坡高几乎没有关系,内摩擦角25°时,不同坡高的滑体倾角仅相差0.18°,内摩擦角为45°时,不同坡高的滑体倾角相差最大,也只有不足3°。

不同坡高时,内摩擦角—滑坡体倾角关系的线性拟合曲线(图10)基本重合,拟合曲线及相关度为

式中,x为内摩擦角;y为滑坡体倾角。

如果把边坡土体完全按照散体看,则其滑坡后滑体的倾角应该是自然安息角[18]。但有很多顺层滑坡,其滑体的倾角远小于组成坡体的岩石破碎后所堆积成的毛石堆的坡角[19](视为自然安息角),这就表明,在顺层滑坡中,要重点关注的是软弱夹层或层面的强度弱化[20],特别是第四系岩土体与基岩的接触面,如果这些优势滑面的内摩擦角或内聚力急剧下降,则会在这些优势面上发生滑坡,而滑后的滑坡体倾角只与这些优势滑面的强度有关,而与组成边坡的岩石块体强度相关度不大。而在滑坡治理时,清坡及对边坡进行加固,都应关注并利用当坡角为αf=(x+φ/2)时所得到的这些线性规律,很好地理解“工程友好三角区△O′FG”所带来的施工便利。

3.5 改进计算模型后的稳定性计算

为更好地研究“工程友好三角区△O′FG”的内在机理,提出如下问题:如果按αf=(36°+φ/2)形成边坡,其稳定性又怎么样呢? 反映在αf=(x+φ/2)公式中,不同边坡高、不同内摩擦角时,x的取值区间为(33.5°,39.3°),最大与最小值间相差5.7°。取x的平均值36°,依照朗肯土压力计算公式仿写成αf=(36°+φ/2)。在内摩擦角确定时,用这一公式计算不同坡高时的滑体坡面角,其值相差是很小的。比如在内摩擦角小于40°时,其误差仅为1.5°。为了回答上述稳定性的问题,同样以表1 中坡高和内摩擦角为基准,按αf=(36°+φ/2)边坡角,形成边坡,其稳定性计算结果如图11。

图11 内聚力—内摩擦角关系曲线[αf=(36°+φ/2)]Fig.11 Relation curve of cohesions and internal friction angle when αf=(36°+φ/2)

图11为在αf=(36°+φ/2)时内聚力—内摩擦角关系曲线。该曲线仍反映了上述已经讨论过的内聚力—内摩擦角的线性负相关关系,坡高与c、φ强度值的正相关关系。不过在此边坡角进行开挖时,所需内聚力更小,比如具备20°的内摩擦角与15.4 kPa 的内聚力的岩体,就可以使12 m、46°开挖的边坡保持极限稳定,而在内聚力为63.4 kPa 时,则可以使50 m、46°的边坡稳定。

在工程实践中,利用这一关系可带来施工中的很大便利。比如北方燕盛公司曾利用此性质,在中石油塔里木盆地满东1#油井的基础施工中成功进行了桩基础的开挖。塔里木盆地的沙漠中,风成沙流动性极强,也即c、φ极小。为防塌坑,用水浸透风成砂,再在其中进行人工挖孔桩施工,按照这种方法,直径1.0 m 的桩基础可以直接开挖,而不用进行任何支护。说明处于流动状态的风成砂,在浸水后其内聚力也可以达到5～8 kPa 以上。对于12 m 高的边坡,按αf=(45°+φ/2)～(36°+φ/2)开挖,所有内聚力在20 kPa以下的岩土边坡都可以达到极限稳定。因此,可以把αf=(45°+φ/2)～(36°+φ/2)称为1 级“工程友好三角区”,把αf=(36°+φ/2)～φ称为2 级“工程友好三角区”。

4 结 论

在研究滑坡体的强度指标c、φ值与滑坡体的坡角、厚度的关系,与边坡的极限高度的关系的基础上,得到一些规律性的认识,可用于边坡的参数设计及滑坡的防治,并引入了“工程友好三角区”的概念,研究发现在此特定的边坡角范围内,只需要很小的内聚力就能使边坡稳定,极大降低了边坡的支护成本。

在采用αf=(45°+φ/2)的边坡角时,需要一定的内聚力才会使边坡处于临界稳定状态,但所需内聚力很小。在此临界稳定状态,滑坡厚度(坡顶宽度和滑坡体最大厚度)和坡体高度几乎是标准的线性关系,厚/高比—内摩擦角之间呈近负线性相关关系,相关系数R2=0.97,但斜率很小,仅为0.009 5,近于平直线。坡体材料内聚力和坡高的线性关系非常突出,相关系数基本上都为1,斜率平均为1.1。滑坡体上缘和下缘连线的滑坡体倾角和内摩擦角有密切的关系,但与边坡高度关系不大。

在以αf=(36°+φ/2)的坡角进行开挖时,所需内聚力更小,一般岩土都可以满足。在工程实践中,可很好地利用上述认识,服务于边坡工程的设计与施工。