关于小学数学几何概念教学的几点思考

顾臖博

江苏省宜兴市丰义小学 214200

数学概念是客观世界中数量关系和空间形式的本质属性在人们头脑中的反映。几何概念是小学数学概念教学中的重要内容，对于发展学生的空间观念具有重要意义。几何概念作为几何的基础知识，是学生解决问题、形成技能的重要基础。然而，几何概念具有较强的抽象性，小学生以形象思维为主，这就意味着学生在认知和理解几何概念的过程中必然要面临不小的挑战。笔者通过理论研究并结合自身工作经验，论述了几何概念教学的基本路径，期望对广大教育同人有所借鉴和参考。

一、联系学生生活，构建概念模型

小学生对于抽象数学概念的理解，往往是从现实生活中的具体事物开始的。因此，在几何概念教学中，教师要基于学生在日常生活中所认知的事物，积极寻找几何概念的“生活原型”，激活学生丰富的生活经验，以帮助学生构建几何概念的数学模型。

（教师拿出一张A4 纸）

师：我们可以把A4 纸看成什么图形？

生：长方形。

师：对。这张纸很薄，如果我们只看其中的一个面，而不考虑它的厚度，我们可以把这张纸看成一个长方形。现在，老师把20 张纸叠加到一起，它变成了什么形状呢？

生1：长方体。

师：生活中有很多物体都是长方体，你能展示收集到的长方体吗？

生2：我找到了一个牙膏盒，它就是个长方体。

解析：(1)Na2S2O5是中学化学教材中从未出现过的陌生物质,但对题干稍加提炼,不难看出该化学方程式的反应物为NaHSO3,生成物为Na2S2O5和H2O,然后配平即可。

生3：我的铅笔盒也是一个长方体。

生4：我的汉语字典也是一个长方体。

……

师：如果我们不考虑这些物体的颜色和材质，只保留它们的形状和大小，那么它们就可以称之为长方体。

“认识长方体”是学生首次学习立体图形，从平面图形过渡到立体图形，是学生认知上的重大飞跃。教师从一张A4 纸说起，通过不断叠加A4 纸，使学生完成从长方形到长方体的认知转变，真正将数学知识“建立在学生的认知发展水平和已有的知识经验基础之上”。其次，学生在生活中会接触到各种各样的长方体，这些生活经验是学生学习新知识的现实起点。教师充分利用这一点，引导学生收集、展示生活中的长方体，这就打通了现实生活与几何概念的沟通和联系，通过生活中的具体事物帮助学生建构长方体的几何模型。

二、在操作活动中，引发深度思考

操作活动是学生智力发展的源泉。几何概念具有很强的抽象性，这就决定了学生认知几何概念的过程是一个主动、复杂的思维过程。因此，教师不能简单地采取“拿来主义”，将课本上的概念原封不动地灌输给学生，而应利用学生已有的生活经验提炼几何概念，抑或让学生通过动手操作来理解数学概念。

比如，在讲到“圆的认识”时，为了使学生深刻理解圆的本质，教师设计了具有鲜明层次性的操作活动：

操作活动1：教师指导学生运用瓶盖和硬币等生活中的实物让学生画圆，并让学生说一说圆是怎样的一种图形。

操作活动2：教师让学生用圆规画圆，并说一说圆规画圆的操作要领，再次总结圆的特点。

操作活动3：教师指导学生运用小图钉、棉线和笔这三个小工具画圆，画完后再次总结圆的特征。

操作活动1 尽管材料很直观生动，但是学生画完圆后对圆的认识仅仅停留在外在特征的感知，不能把握圆的本质特征；操作活动2 能够揭示圆“一中同长”的本质特征，但是圆规作为一种画图工具，圆的本质是隐藏的、含蓄的，学生并不容易感受到；操作活动3 的材料看上去“简陋”些，但是它生动地还原了圆规画圆的基本原理，将圆的本质特征直观生动地展现出来，使学生看得见、摸得着，对圆的理解自然就更加深刻了。

教学中，为了引导学生理解圆“一中同长”的本质，教师安排了层层递进的操作活动，圆的本质属性在动手操作和动脑思考中逐渐显露出来，从而起到了化抽象为具体的教学功效，也使学生对圆的本质理解变得水到渠成。

三、在辨析比较中，感悟概念内涵

教育家乌申斯基说：“比较是一切理解和思维的基础，我们正是通过比较来了解世界上的一切的。”在小学数学教材中，考虑到小学生认知水平的局限性，教材对几何概念的定义往往是建立在实物或者直观图示的基础上，这虽然有利于学生对概念的理解和掌握，但是也容易让学生把教材中出示的图形作为几何概念的唯一解释，从而形成对几何概念理解的思维定式。这个时候，教师要把正面揭示概念本质和变式材料相结合，不断改变几何概念的表现形式，使其非本质属性时有时无，而本质属性却保持恒定，从而引导学生在辨析和对比中厘清概念的内涵和外延。

比如，在讲到“认识梯形”时，教材中明确指出“只有一组对边平行的四边形叫梯形”，但是部分学生仍然将图1作为心目中标准的梯形。教师为学生出示图2，让学生判断这些图形是否是梯形。这个时候，有的学生错误地判断这些图形不是梯形，究其原因就是学生将梯形的非本质属性（比如两条平行线的长短和位置、两腰相等、有两个角是直角等）当成了本质属性。此时，教师引导学生对梯形的概念展开辨析，就能使学生对梯形概念的理解更加精准。

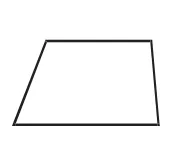
图1

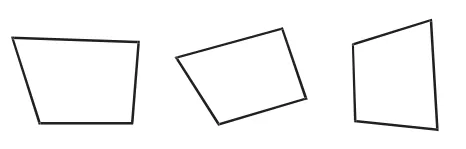
图2

又如，在讲到“认识梯形的高”时，教师首先为学生出示梯形的高，然后通过多媒体对梯形进行旋转变换（如图3），让学生判断虚线是否仍然是这条底上的高。在学生做出肯定的回答后，教师进一步引导学生思考：“为什么经过旋转，这条虚线仍然是这条底所对应的高呢？”学生通过分析讨论得出如下结论：只要是从上底的一点向下底作垂线，这个点和垂足间的线段长就是这条底上的高。最后教师引导学生判断：（如图4）竖着的这条虚线是梯形的高吗？为什么？学生在辨析比较后认为，这条虚线并非上底任一点到下底的垂线段，因此不是梯形的高。这样学生就建立了丰富的“梯形的高”的表象，理解了高的本质属性。

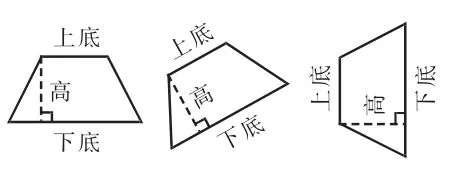
图3

图4

四、在概念强化中，促进知识建构

马芯兰老师在《马芯兰小学数学能力的培养与实践》 一书中指出：“课堂教学要根据学生的认知特点，按照思维过程的规律展开，要给予起决定作用的核心概念以核心的地位，并在建立、运用和深化这些概念的过程中，勾连知识之间的内在联系，沟通数量之间的内在关系，使学生在不断完善知识网络的过程中，形成良好的认知结构。”几何概念并非人们直观看到的零碎、孤立和分散的状态，而是密切联系着的。因此，教师在教学时要帮助学生对几何概念进行归纳和梳理，让学生经历分类的过程，把相关的几何概念贯穿起来，从而形成比较系统的认知结构。

比如，在讲到 “认识平行四边形”时，教师为学生出示图形（图5），要求学生完成如下任务：“如果用一个大圈表示所有的四边形，那么 ‘平行四边形’‘长方形’‘正方形’是其中哪个圈？请你在图中填一填，并说明理由。”学生在讨论后认为，平行四边形有两组对边互相平行，它是一种特殊的四边形，所以它应该填在左边大圈中；长方形不但是两组对边互相平行，而且四个角都是直角，因此，长方形是特殊的平行四边形，它应该填在平行四边形里面的那个圆中；正方形又是特殊的长方形，所以它应该填在左边最小的圆中。然后教师进一步追问：“平行四边形是特殊的四边形，那么它为什么不填在右面的大圈里，却要填在左边的大圈里呢？”学生经过讨论后认为，如果把平行四边形填在右边的大圈里，那就不能体现出平行四边形、长方形和正方形之间的关系了。

图5

与教师直接为学生呈现韦恩图相比，教师要求学生自己建构韦恩图的教学方式更能激发其思考，给予其深刻的印象。教学中，教师为学生呈现一幅完整的韦恩图，要求学生在圈子数多于图形种类的图中进行思考和判断，使学生经历了迷茫、困惑甚至失败之后，正确地建构起四边形、平行四边形、长方形和正方形之间的关系，由此形成对知识的系统性认识，进而将“新概念”建立在原有的“旧概念”的基础之上。

几何概念教学是一个值得深入挖掘和不断探索的课题。在几何概念教学中，教师要激活学生已有经验，关注学生直观感受，把动手操作和动脑思考结合起来，通过辨析和比较使学生获得对概念的精准理解，并在概念的贯通和联系中，帮助学生建构起完整的知识框架。