基于高斯过程回归的双切圆燃煤锅炉烟气含氧量预测

俎魏锋

（广东大唐国际雷州发电有限责任公司，广东 湛江 524255）

0 引言

烟气含氧量是评价燃煤电厂的一个重要指标。烟气含氧量过高表明总风量过大，进而导致排烟热损失增加，锅炉效率降低；烟气含氧量过低则表明炉内空气量不充分，煤粉燃烧可能处于缺氧状态，进而增加CO含量，导致水冷壁高腐蚀。烟气含氧量涉及多种影响因素，包括负荷、总风量、一次风温度以及二次风温度等因素。锅炉的大迟滞特性会在操作条件发生变化时导致烟气含氧量不能及时发生变化。除此之外，传统烟气含氧量测量工具包括氧化锆烟气传感器和磁式氧气传感器等，这些传感器成本较高，且测量环境灰含量较高，容易造成测量原件的腐蚀，导致测量不准确。

为实现烟气含氧量的准确、及时测量，已有研究人员利用锅炉历史数据，使用最小二乘支持向量机模型、人工神经网络和支持向量机建立了烟气含氧量预测模型，并且有较高的预测精度。高斯过程回归同样是一种数据驱动的机器学习回归模型，以往研究表明具有良好的预测能力。该文利用历史运行数据，对1000 MW超超临界双切圆煤粉锅炉建立高斯过程回归烟气含氧量预测模型。

1 高斯过程回归模型介绍

1.1 高斯过程回归模型原理

高斯过程回归是使用高斯过程对输入参数进行先验回归分析的预测模型。相较于其他回归模型，高斯过程回归严格依照概率统计理论，可对预测值输出置信区间。当样本数量较少时，高斯过程回归相比于其他预测模型有更好的预测精度，高斯过程回归模型的解释性更好，而且整体模型较为简单。高斯过程可由均值函数（）和协方差函数（，'）共同来定义，如公式（1）所示。

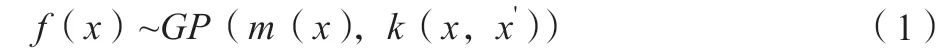
式中：（）为高斯过程潜在函数；（）为均值函数；（，'）为协方差函数。

设观测值为，则观测值和潜在函数（）之间的关系如公式（2）所示。

式中：为噪声，且满足如公式（3）所示的正态分布。

式中：为方差。

（）满足如公式（4）所示的联合高斯分布。

一般情况取均值为0，∑为的协方差函数。因此观测值的先验分布如公式（5）所示。

式中：为单位矩阵。

输出和预测输出的联合分布，服从如公式（6）所示的高斯分布。

式中：（，）为输入样本x的×协方差矩阵；（，）=（x，）为输入值和新输入值之间的×1阶协方差矩阵。

预测值的均值如公式（7）所示。

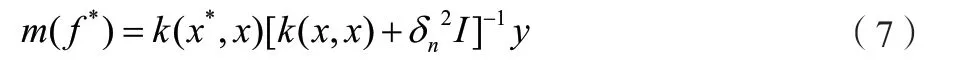
预测值的方差为公式（8）所示。

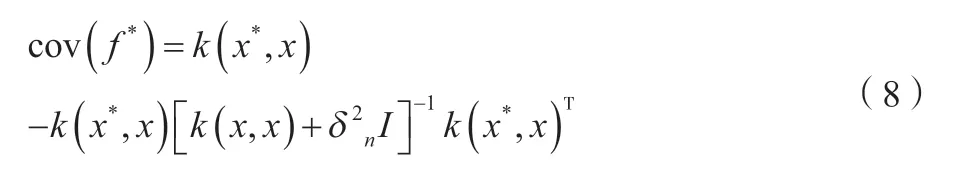
1.2 算法模型实现过程

使用过滤方法进行数据特征选择，确定训练样本的输入向量个数，建立预测模型的训练样本（，）。进行数据清洗，删除或修补数据集中的空值，使数据集完整。然后进行数据标准化处理。当数据数量级相差较大时或离散性较大时，需要对输入、输出数据进行标准化处理：各训练样本的输入值除以所有样本在各维度上的标准差；对输出进行标准化处理，推荐的标准化方法是对各样本输出减去所有样本输出的平均值。高斯过程回归核函数主要包括平方指数核函数、有理二次核函数和matern核等，因为平方指数核函数可应用于绝大多数场景，并且无限可微，所以可以无限次求导并始终连续，该研究采用平方指数核函数。数据选取并预处理。根据机组常用负荷，选取稳定负荷区间运行数据。对数据各参数进行相关性分析，根据氧量的相关性系数，选取元素作为输入参数，氧量作为输出标签参数，并使用程序语言框架对训练样本进行训练。对基于高斯回归模型的训练的数据进行预测并得出结果，进一步验证所建立模型的精度情况，并对所建预测模型的鲁棒性进行检验。

1.3 锅炉形式说明

该文的研究对象为某1000 MW二次再热锅炉超超临界锅炉，采用双切圆燃烧方式。二次再热、平衡通风、露天布置、固态排渣、全钢构架以及全悬吊结构Π型锅炉。锅炉中速末正压直吹式制粉系统，配备6台磨煤机，主燃烧器布置在水冷壁前后墙上，每层8只燃烧器对应一台磨煤机。

1.4 输入参数选择和数据预处理

锅炉常规运行工况负荷在450 MW以上，试验数据选取负荷为450 MW～1000 MW。同时因锅炉变负荷工况锅炉调节存在滞后性，氧量波动较大，该研究以锅炉稳态工况作为研究对象。锅炉稳态判断依据为机组负荷最大允许波动范围±1.0%；锅炉蒸发量最大允许范围±1.0%，锅炉主蒸汽压力最大允许波动范围±1.0%。

由于锅炉燃烧过程是一个强耦合过程，烟气含氧量涉及多种因素，包括负荷、配风方式、配煤方式和配风温度等，因此要选择和烟气含氧量相关程度最大的变量作为模型的输入变量。

为降低运算复杂程度，对变量进行相关性分析。相关系数是能反应变量之间相关性的重要指标。该文采用皮尔逊（pearson）相关性系数检验系数相关性。皮尔逊相关性系数又称皮尔逊积矩相关性系数，表示2个变量和的相关性。相关性系数的取值为[-1，1]。其计算公式如公式（9）所示。

式中：cov（，）为和的协方差；var[]为的方差；var[]为的方差。

部分相关性系数计算结果见表1。

表1 烟气含氧量相关性系数

根据相关性系数，该文选择烟气再循环风量、一次风风量、一次风温度、二次风风量、二次风温度、总煤量和机组负荷作为高斯过程回归的输入参数，烟气含氧量作为输出参数，建立的高斯过程回归模型如图1所示。

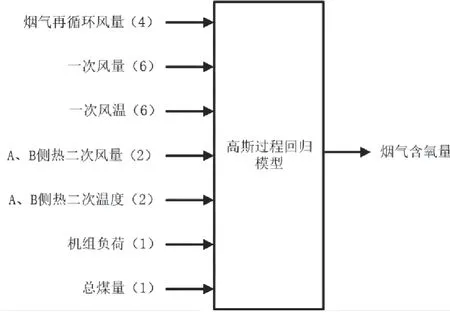
图1 高斯过程回归模型

部分机组参数见表2。从302组样本中随机选择272组作为训练集，30组组为测试集。利用R2评估预测的准确性。由于不同输入参数的量纲差异较大，因此对输入参数进行归一化处理，归一化公式如公式（10）所示。

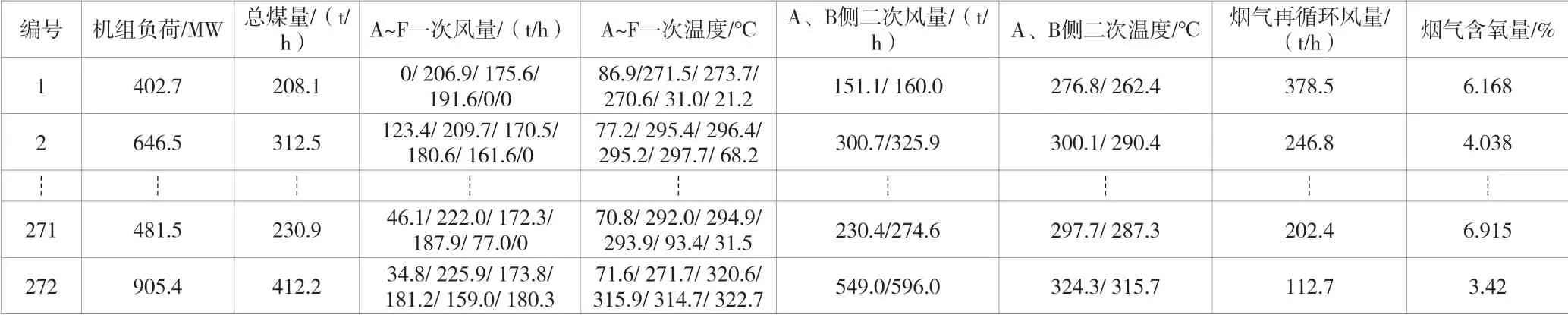
表2 部分样本参数

式中：x为第组元素值；为该元素最大值；为该元素最小值。

2 模型结果分析

以1 min为间隔选取302组历史数据，划分为训练集和测试集，训练集完成对高斯过程回归模型的创建，测试集对模型进行验证。

利用建立好的高斯过程回归模型，对测试集的30组结果进行预测。验证建立的模型的精度，测试集预测结果如图2所示，预测的相对误差如图3所示。

测试集的机组负荷变化为450.5 MW～990.2 MW，烟气含氧量在3%到7%之间变化。从图2、图3可以看出，尽管烟气含氧量变化范围较大，建立的高斯过程回归模型内能够对烟气含氧量进行较为准确的预测，大部分样本的训练误差都在3%以内，且围绕0均匀分布。最大的预测误差对应于11号测试集样本，最大误差为3.74%。训练集的R2为0.977012。

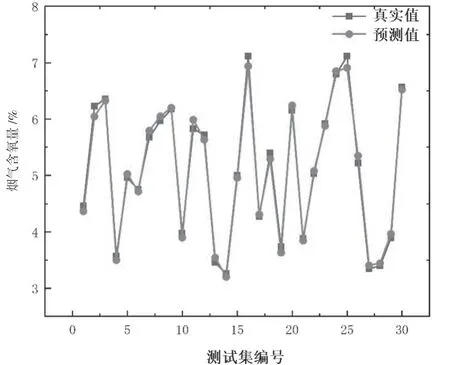
图2 测试集预测结果

图3 测试集相对误差

建立的高斯过程回归模型涉及较多的输入变量，而且炉内燃烧较为剧烈，在锅炉实际运行过程中很有可能测量某个变量的传感器发生故障导致测量结果不准确，尤其一次风量、二次风量和烟气再循环风量等参数时常波动，容易导致烟气含氧量预测值出现偏差。为了避免这种情况发生，建立的高斯过程回归模型需有良好的鲁棒性，即在部分输入变量发生微小波动时，预测的烟气含氧量仍有较高的预测精度。对建立的预测模型的鲁棒性进行检验，对测试集每个样本的22个变量中的任意11个变量施加1%到10%的随机扰动，验证增加了随机扰动后的预测精度。结果如图4和图5所示。

从图4、图5可以看出，对输入变量增加随机扰动后，烟气含氧量预测的相对误差相比未施加扰动时有所增加，预测的相对误差的最大值6.69%，证明增加扰动会对高斯过程回归烟气含氧量预测精度产生一定的影响。尽管如此，预测相对误差的绝对值的平均值为3.70%，仍然有较高的预测精度。且对22个输入变量中的11个变量施加了扰动，在电场实际运行中出现大量传感器测量误差较高情况的概率很小，因此可以证明建立的高斯过程回归模型的鲁棒性较好。

图4 增加扰动后测试集预测结果

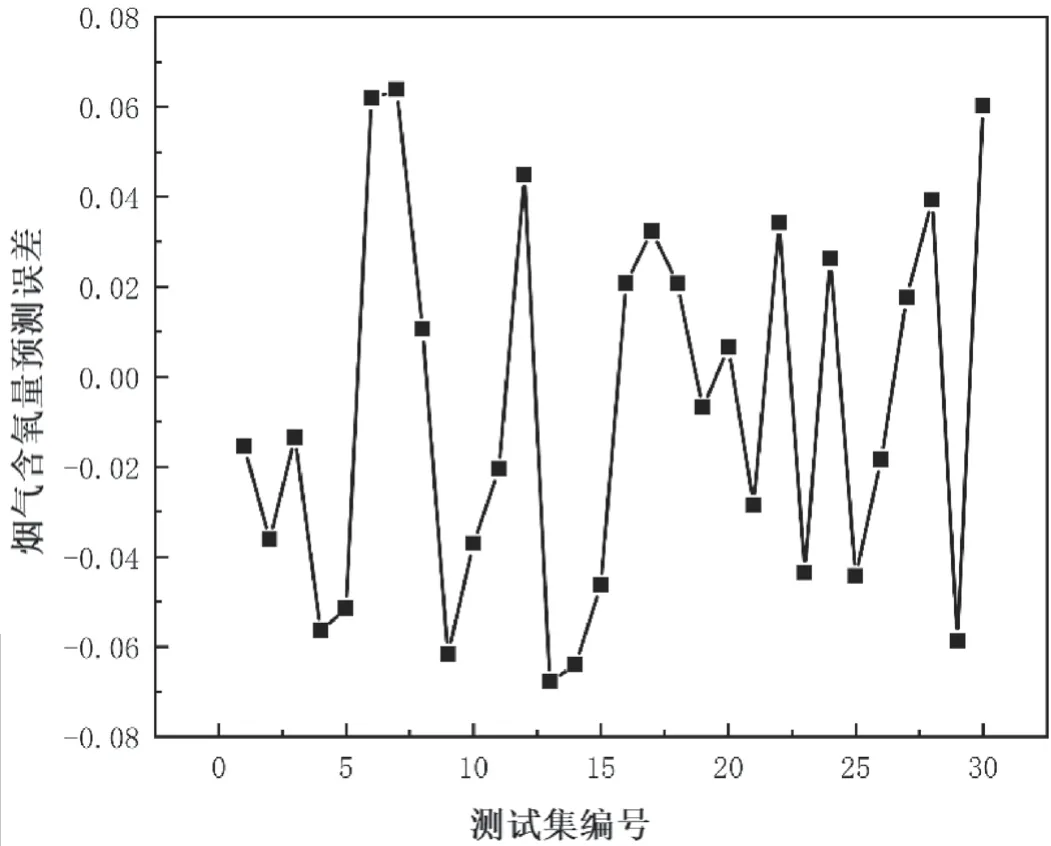
图5 增加扰动后测试集相对误差

3 结论

针对燃煤电厂烟气含氧量测量成本高且难以测量准确的问题，该文建立了高斯过程回归模型，以烟气再循环风量、一次风风量、一次风温度、二次风风量、二次风温度、总煤量和机组负荷作为模型的输入，烟气含氧量作为模型的输出。对测试样本的准确性进行了验证，结果表明建立的模型预测精度较高。然后对模型的3鲁棒性进行研究，对部分输入参数施加随机扰动，评估增加扰动后预测的准确性，结果表明预测误差有一定增大，但准确性仍然较高。建立的预测模型可以为现场工作人员提供有效的参考，并需要与现场烟气含氧量测量结果进行对比，及时判断现场传感器是否发生故障。