土壤中污染物溶质运移模拟

喻 佳 魏善彪

（1．江西核工业环境保护中心，江西 南昌 330002；2．江西省地质局实验测试大队，江西 南昌 330002）

该文以某火电厂脱硫废水收集池为例，运用Hydrus-1D，选用连续与非连续点源两种模式，对比分析氟化物在土壤中的迁移特征。

Hydrus-1D是用于模拟饱和—非饱介质中水流运动、热量迁移、溶质运移的软件，其控制方程采用有限元法求解，模拟区域既可以是不规则的水流边界组成的区域亦可以是各项异性的非均质土壤颗粒组成的区域。国内也有很多学者利用Hydrus-1D研究土壤中污染物的运行，如许雪婷、叶永红、丁素玲等。

1 土壤中水流和溶质运移控制方程

Hydrus-1D包括水流入渗、溶质运移、根系吸收、热运移等模块。根据污染物在土壤中的迁移特征，该文选择水流入渗、溶质运移两个模块。

1.1 水流运动控制方程

Richards为经典方程，其同时考虑到了地下水补给和数学求解等多方面的影响，还能够模拟水分在土壤中的动态变化。Hydrus-1D即采用Richards方程，其控制方程见公式（1）（土壤水分特征曲线）和公式（2）（土壤导水率）。

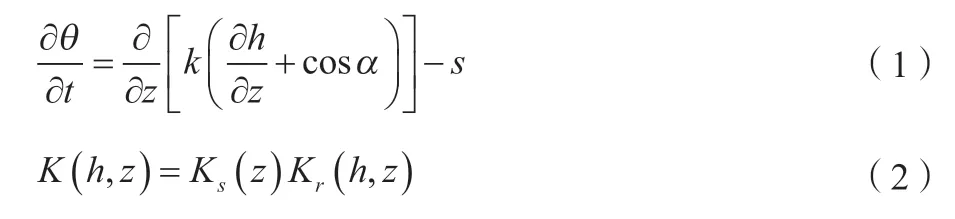
式中：为土壤体积含水量，cm/cm；为压力水头，cm，饱和带大于0，非饱和带小于0；为垂直方向坐标；为时间变量，s；为非饱和渗透系数函数，cm·d；为作物根系吸水率，cm·cm·s，不考虑根系吸水时，=0；为水流方向与垂直方向夹角（=0为垂直流，=90°表示水平流，0<<90°表示倾斜流）；K为相对导水率，cm·d；K为饱和导水率，cm·d。

土壤水分特征曲线和土壤导水率可以使用van Genuchten、Brooks-Corey及Kosugi等模型在Hydrus-1D中拟合。Van Genuchten模型由于适用范围广、模拟精度高，已被广泛使用到不同的模拟情形中，因此，在土壤研究中应用较广。该文忽略水流滞后现象，采用van Genuchten模型进行计算。Van Genuchten模型见公式（3）。

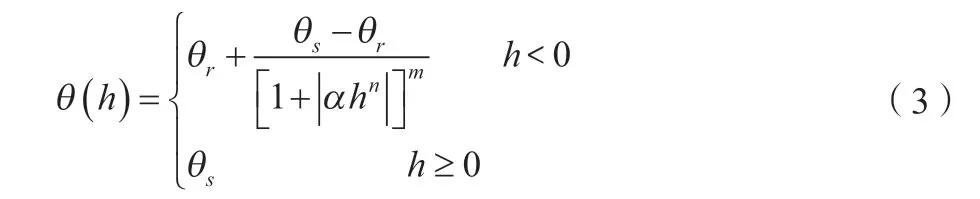
式中：θ为残余含水量；θ为饱和含水量；为进气吸力值的倒数；为孔径分布参数；=1-1/n；为压力水头。

Hydrus-1D中土壤水分运动控制方程定解条件包括初始条件和边界条件。

初始条件可用初始压力水头h和土壤含水率表示，其控制方程式见公式（4）和公式（5）。

边界条件包括以下3种情况：

第一类边界条件（Dirichlet）：变量已知边界，主要适用于压力入渗（地表存在薄层积水）及强烈蒸发（表土达到了风干含水率）。

第二类边界条件：水流通量已知边界，主要适用于降雨、蒸发强大已知的边界，灌水入渗，不透水边界及无蒸发入渗边界。

第三类边界条件：水流通量随边界上的变量或h而变化的情况。

1.2 溶质运移控制方程

溶质运移控制方程见公式（6），该方程未考虑污染源的密度变化，忽略了溶质的吸附、解析及自然衰减等物理、化学、生物反应，仅考虑了对流及弥散作用。

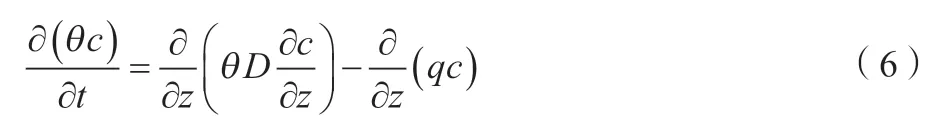
式中：为污染物介质中的浓度，mg/L；为弥散系数，m/d；为渗流速率，m/d；为沿轴的距离，m；为时间变量，d；为土壤含水率，%。

初始条件如式（7）所示。

边界条件如下。

第一类Dirichlet边界条件如式（8）和式（9）所示。

该条件适用于非连续点源。

第二类Neumann零梯度边界如公式（10）所示。

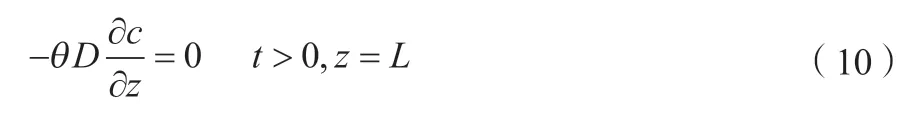
2 研究区概况

该文以某火电厂为研究对象，其土壤环境为污染型项目，土壤环境污染包括大气沉降及垂直入渗，该文主要研究垂直入渗情况对土壤环境的污染。火电厂垂直入渗污染源包括废水处理建构筑物、氨水储罐等，该研究选取脱硫废水收集池进行预测。脱硫废水收集池泄漏选取的预测因子为氟化物，浓度为50mg/L。

根据建设项目岩土工程勘察报告，脱硫废水收集池底部土壤岩性为黄土状粉土，厚度为4.1m。

3 土壤中氟化物运移模型

3.1 土壤厚度

脱硫废水收集池土壤岩性为黄土状粉土，厚约4.1m。因此，以地面作为高程零点，研究区土壤厚度划分为一层，高程为0cm～-410cm，设置5个观测点位，分别位于-82cm（N1）、-164cm（N2）、-246cm（N3）、-328cm（N4）、-410cm（N5）处。

3.2 边界条件

上边界：假定脱硫废水收集池底部防渗层发生破损，废水持续泄漏，选用第一类Dirichlet边界条件中的连续点源边界，即上边界泄漏浓度=50mg/L；假定脱硫废水收集池底部防渗层出现破损，企业实际运行时，废水处理构筑物每年检修一次，一旦脱硫废水收集池底部防渗层发生破损，检修时即会发现，因此，泄漏时间为365天，365天后切断污染源，废水不再泄漏，选用第一类Dirichlet边界条件中的非连续点源边界，即0～365天泄漏浓度=50mg/L，365天以后泄漏浓度为=0mg/L。

下边界：假设潜水面随时间变化较小，可以忽略不计，则下边界设为压力水头为零的第一类边界条件（Dirichlet）。

图6可以看出，甲醇含量越高，苦杏仁苷提取得率越大，野黑樱苷提取得率越小。当甲醇含量≥90%时，提取溶液中几乎检测不到野黑樱苷。说明水的存在可能对苦杏仁苷有分解作用，产生分解产物野黑樱苷，所以研究选取甲醇作为提取溶剂，尽量避免降解原料中苦杏仁苷成分。同时对图5中相对保留时间在21.9 min和35.6 min的物质成分进行了分析并确定为其降解产物成分。

3.3 参数设定

使用Hydrus-1D对土壤中污染物进行研究须输入土壤特征参数和运移参数。土壤特征参数包括土壤的残余含水量、饱和含水量及土壤水力曲线参数等水分参数。运移参数包括渗透系数及弥散系数等。

该文建立的模型忽略土壤对氟化物的吸附及氟化物在土壤中的物理、化学、生物反应，仅考虑对流及弥散作用。使用Van Genuchten方程进行溶质运移平衡计算。各参数采用软件中相应土壤的经验参数值，具体参数见表1。

表1 模型计算主要参数表

3.4 初始条件

假定土壤中氟化物的浓度为0。

3.5 时间设置

模拟预测时间设定为脱硫废水收集池废水发生泄漏后100天（T1）、365天（T2）、1000天（T3）、2000天（T4）、3650天（T5）。

4 模拟结果分析

4.1 脱硫废水收集池废水连续泄漏（情景1）

根据脱硫废水收集池土壤岩性及连续泄漏条件设置的参数、边界条件等建立了模型，预测结果如图1和图2所示。

由图1可知，土壤中同一观测点，废水发生泄漏垂直入渗进入土壤时间越长，土壤中氟化物浓度越高，反之，土壤中氟化物浓度越低，土壤中污染物浓度与泄漏时间呈正相关；不同观测点，同一时间，污染物逐渐自地面向潜水面迁移，随着泄漏时间推移，近潜水面土壤中氟化物逐渐接近其泄漏浓度。

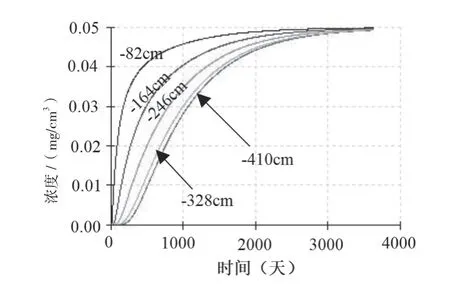
图1 不同时间点氟化物浓度随深度变化图（情景1）

由图2可知，同一时间，自地面至潜水面，土壤中氟化物浓度逐渐减少，反之，土壤中污染物浓度越高，土壤中污染物浓度与深度呈负相关；不同时间，自地面至潜水面，随着时间推移，土壤中氟化物逐渐向下迁移，近潜水面土壤中氟化物浓度逐渐增大直至接近泄漏浓度。

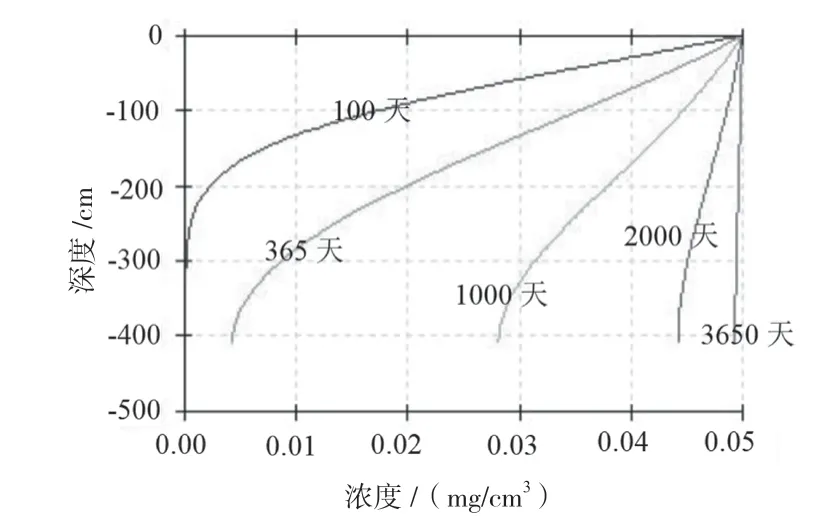
图2 不同观测点氟化物浓度随时间变化图（情景1）

4.2 脱硫废水收集池废水非连续泄漏（情景2）

根据脱硫废水收集池土壤岩性及非连续泄漏设置的参数、边界条件等建立了模型，预测结果如图3和图4所示。

由图3可知，脱硫废水收集池废水发生泄漏后，同一观测点处土壤中氟化物浓度先逐渐升高，达到峰值后，土壤中氟化物浓度逐渐降低，趋近于0，对土壤环境影响逐渐减少；不同观测点处，同一时间，在各观测点氟化物浓度达到峰值之前，土壤中氟化物浓度逐渐升高，反之，逐渐降低，随着时间推移，趋近于0。

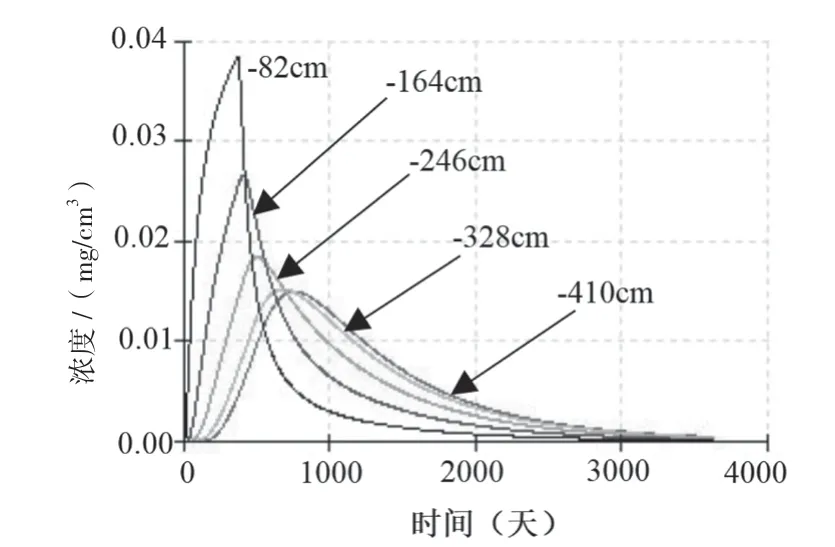
图3 不同时间点氟化物浓度随深度变化图（情景2）

由图4可知，0天～365天连续泄漏期间（泄漏浓度为50mg/L），相同时间，自地面至潜水面，氟化物逐渐向潜水面迁移，对土壤环境的影响深度逐渐增加；同一观测点位，泄漏时间越长，土壤中氟化物浓度越大。365天以后（泄漏浓度为0），相同时间，自地面至潜水面，氟化物逐渐增大，浓度远低于泄漏浓度；同一观测点位，泄漏时间越长，土壤中氟化物浓度越小，时间越长，越趋近于0。

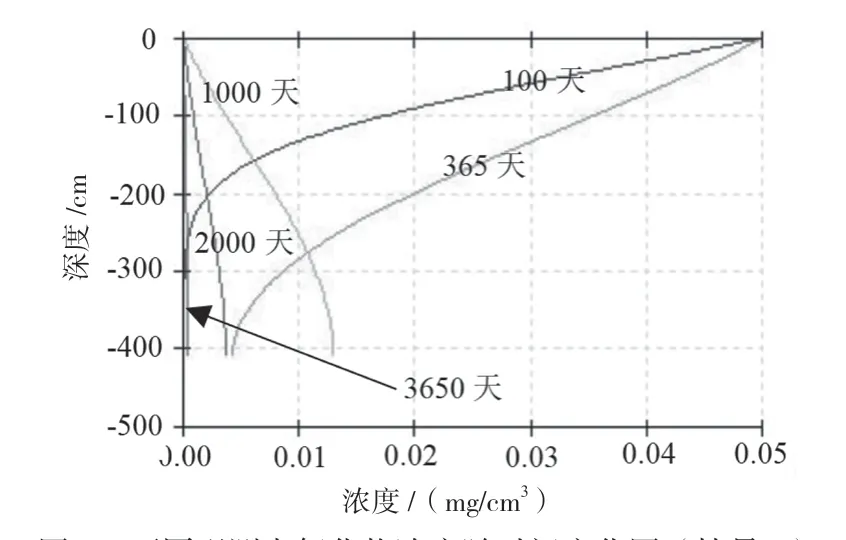
图4 不同观测点氟化物浓度随时间变化图（情景2）

由上述预测结果可知：选用连续点源模式进行预测，废水发生泄漏后，自地面至潜水面土壤中污染物浓度逐渐升高，泄漏时间越长，土壤中污染物浓度越趋近于污染物泄漏浓度，对土壤环境的影响较大。选用非连续点源模式进行预测，废水发生泄漏后，在连续泄漏时间内，自地面至潜水面土壤中污染物迁移特征与选用的连续点源模式预测结果一致，达到峰值（峰值小于泄漏浓度）；废水不再泄漏后（泄漏浓度为0），污染源切断，进入土壤中的污染物作为仅有的污染源逐渐向潜水面迁移，随着时间的推移，由于土壤中对流及弥散作用，近潜水面土壤中氟化物浓度逐渐趋近于0，对土壤环境影响很小。

该方法可定量预测废水或废液泄漏后污染物在土壤中的垂向变化情况，可以作为土壤环境高等级评价污染型建设项目的连续与非连续点源土壤溶质运移模拟预测的一种参考。

5 结论

该文以某火电厂脱硫废水收集池为例，运用Hydrus-1D，选用连续与非连续点源两种模式，对比分析氟化物在土壤中的迁移特征。对比预测结果可知，如不考虑实际情况，直接选取连续源边界条件，预测结果对土壤环境的影响远大于其实际对土壤环境的影响；根据实际情况，选用非连续点源边界条件对可通过构筑物检修等途径发现泄漏的这类事故情景进行预测更合理，更能反应土壤中污染物浓度变化情况，更贴合建设项目实际运行发生非正常工况对土壤环境的影响。

该文建立的模型只考虑了土壤中对流及弥散作用对污染物的扩散影响，没有考虑土壤吸附、生物降解及化学反应等作用对污染物的转化影响，预测结果值比实际值偏高，后续的研究将尽量将上述影响因素考虑在内。另外，土壤与地下水环境影响评价应该是紧密连接的，土壤预测结果应作为地下水环境影响预测的输入源强，下一步研究方向将考虑把土壤环境影响预测与地下水环境影响预测有机结合在一起。