有机/无机杂化钙钛矿太阳能电池S形电流扭结的集总参数等效电路模型
2022-11-07刘竞贤陈考铭马韵涵黄君凯邓婉玲
刘竞贤,陈考铭,马韵涵,黄君凯,邓婉玲
(暨南大学信息科学技术学院,广东 广州 510632)
当前能源危机日趋严重,寻找一种清洁且可持续发展的能源至关重要。光伏发电系统可将太阳能转换成电能,并且具有可再生、无污染和储量大等优点,而得到广泛地应用[1]。众多研究者致力于制备出高转换效率的太阳能电池,其中硅基太阳能电池由于良好的转换效率一直占据着主要的光伏市场[2],但是由于高昂的制备成本,越来越多的研究人员将目光转向了有机/无机杂化钙钛矿太阳能电池的开发。钙钛矿太阳能电池是以钙钛矿有机卤化金属材料作为吸光材料的一种低成本电池[3-5],通过寻求合适的材料用作电子和空穴传输层,并通过调整器件结构、更新薄膜沉积技术和采用界面调控等方面的研究,从而实现较高的光电转换效率[6-7]。
然而,在有机/无机杂化钙钛矿太阳能电池的制备中,会出现一种严重损害电池转换效率的特殊曲线,即S形电流电压曲线。为了更准确地对太阳能电池进行模拟研究,通常采用集总参数等效电路模型仿真和软件模拟常规电流电压曲线或特殊的S形曲线。为提高有机太阳能电池的功率转换效率(Power Conversion Efficiency,PCE),研究人员不断开发和完善太阳能电池等效模型[8-9],期待探索并解决所出现的问题。单二极管模型[10]结构简单,但是只能模拟常规的电流电压曲线,而双二极管模型比单二极管模型更准确,但是其求解的难度也更大[11],所以在常规伏安特性的模拟中最常用的模型还是单二极管模型。为了实现对S形曲线的模拟,研究人员提出了更加复杂的模型。Mazhari等[12]提出的三二极管模型虽然可以描述S形扭结,但其模拟结果不够准确;Pozo等[13]提出了一个包含两个子电路的模型,该模型只需要两个二极管就可以描述S形扭结,却无法拟合第一象限中呈指数上升的曲线;García-Sánchez等[14]针对多子电路模型提出改进方案,不仅可以实现第一象限中指数上升曲线的拟合,而且还建立了电流-电压的显式方程,但该方程只能在一些限定条件下进行求解,给模型的应用带来了限制。因此,开发一个准确且解析的模型至关重要。
本文在文献[15]研究结果基础上提出了一个改进的等效电路模型,该模型不仅可以获得模型的显式算法,还可验证对指数型上升实验数据的拟合能力。
1 集总参数模型的改进
在Mazhari模型基础上提出的等效电路模型,即钙钛矿太阳能电池的集总参数等效电路模型[15]如图1所示。从图1可见,该模型可分为光生电流电路(Photo Generated Current Circuits,PGCC)和载流子复合电流电路(Carrier Recombination Current Circuits,CRCC)两个部分。PGCC电路中包括光生电流Iph、复合电流二极管D R和提取电流二极管DE,CRCC电路描述了欧姆接触和陷阱态的影响,也即使用二极管DD1和D D2分别表示正向和反向电压情况下对载流子陷阱态的捕获情况,使用电阻RC1和RC2表示欧姆接触的影响。该模型可更加准确地描述电流S形扭结,并且可以得到电流-电压的显式表达式,但模型中只有两个用于模拟欧姆接触的串联电阻,而没有任何并联电阻的存在。

图1 钙钛矿太阳能电池的集总参数等效电路模型[15]Figure 1 Lumped parameter equivalent circuit model of perovskite solar cells
为了进一步提高该模型的准确性,进行了如图2所示的改进,即在由内部电场引起的提取电流DE支路中增加了一个分流电阻RE。分流电阻一方面可以用来表征将电荷提取到电极上带来的部分电流损耗,另一方面与二极管DE来共同表征提取电流IE,进一步提高模型的准确性与完整度。
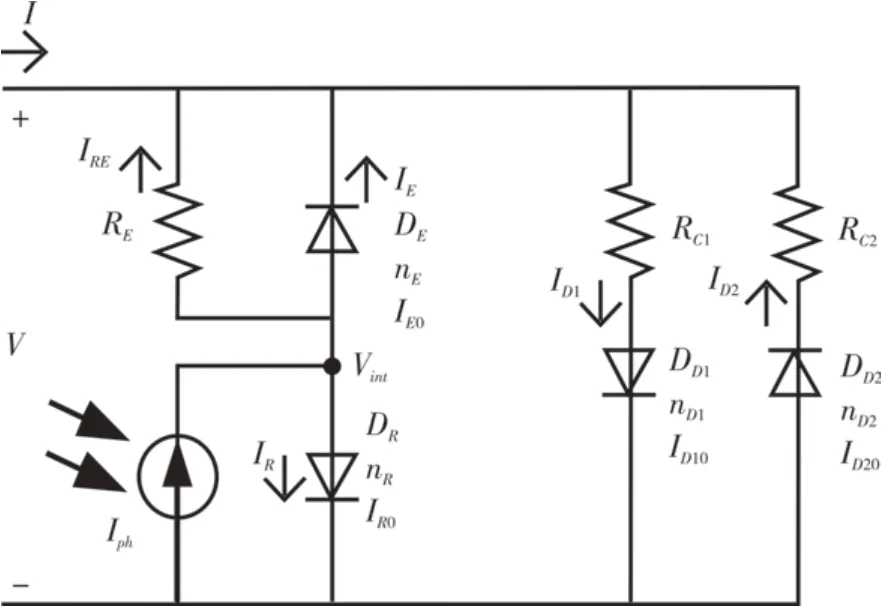
图2 改进的钙钛矿太阳能电池的集总参数等效电路模型Figure 2 Improved lumped parameter equivalent circuit model of perovskite solar cell
针对改进的集总参数等效电路模型,根据基尔霍夫电流定律和欧姆定律,以及结合肖克利理想二极管电流方程[16],整合可得如下公式。
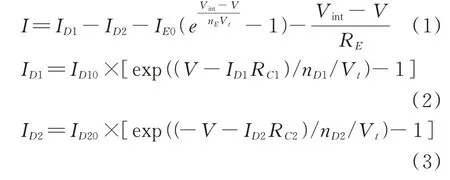
式(2—3)中:ID1和ID2分别为流经所在支路的电流,ID10和ID20分别表示二极管DD1和DD2的反向饱和电流,nD1和nD2分别是两个二极管的理想因子;V t是热电压,V t=kT/q,其中k是玻尔兹曼常数、T是环境温度、q是电荷量。ID1和ID2的方程满足W0(x)exp(W0(x))=x要求,利用Lambert W函数可以导出ID1和ID2的解析解,其中W0是Lambert W函数的主分支[17]。

从式(1)可知,即使得到了ID1和ID2的解析解,仍无法获得电流的显式解析解,因此作为中间值的结点电压Vint至关重要,需要先求得其显式方程。根据图2等效电路的左侧拓扑结构,结合基尔霍夫电流定律和肖克利理想二极管电流方程,可以得到如下公式。

显然,式(6)除了结点电压Vint之外都是已知量,但该式是一个包含了两项指数项的超越方程,结合式(1)和式(6)来求解过于复杂,无法得到关于电压函数的电流表达式。同时,式(6)既无法使用常规方法直接求解,也无法使用Lambert W函数进行计算,故使用分区方法来求解Vint的表达式[18]。在反向端电压的情况下,复合电流IR比提取电流IE小得多,可以忽略不计,故I远大于,因此可得下式。

虽然式(7)仍然是一个超越方程,但右侧只有一个指数项,因此可利用Lambert W函数进行求解,获得在反向端电压情况下结点电压Vint1的表达式。
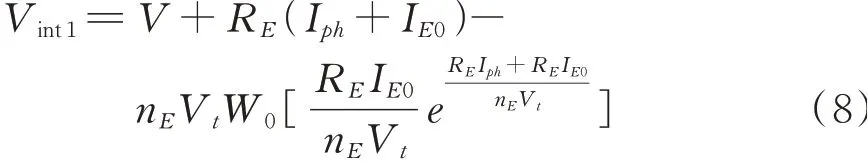
同时,在正向电压的情况下,提取电流IE比复合电流IR小得多,故远大于,可以得到:

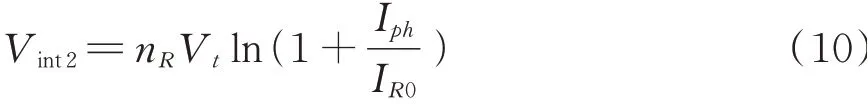
因此,可得在正向端电压情况下结点电压Vint2的表达式。
为了得到适用于整个工作区域的Vint表达式,采用光滑函数连接Vint1和Vint2,同时使用Schroder级数的修正以提高Vint的准确性[19-20]。最后,可以得到Vint的表达式。

式(11)中ω=(y/y′)/(1-0.5yy′/(y′)2),其中y′和y′分别是y关于Vint的一阶导数和二阶导数。最后,分别将式(4)、式(5)和式(11)代入式(1)中进行求解,可以得到电流-电压的显式解析式。

2 结果及讨论
为验证分区方法求解结点电压Vint算法的准确性,运用最小二乘法对Vint进行求解,同时也采用分区方法进行处理,即通过公式(8)、(10)和(11)进行计算,2种方法所获得的结点电压Vint对电压V的曲线如图3所示。从图3可见,最小二乘法和分区方法对结点电压计算结果的偏差可满足要求,因此可以使用分区方法对结点电压进行有效求解。

图3 最小二乘法和分区方法对结点电压求解结果的比较Figure 3 Comparison of the solution results of node voltage using least square method and partition method
本文的改进模型中增加了一个分流电阻RE,为了研究RE对伏安特性曲线的影响,图4所示为不同数值分流电阻的伏安特性曲线。从图4可以看到,RE主要影响曲线的扭结部分,并且RE的电阻值越大,扭结的弯曲程度也会变得更加严重。

图4 分流电阻RE对改进集总参数电路模型I-V特性的影响Figure 4 Effects from RE on I-V characteristics simulated by our improved lumped-parameter circuits
从物理意义方面来看,钙钛矿太阳能电池吸收光后会产生激子,激子扩散到最近的钙钛矿与电子(空穴)传输层界面并解离形成极化子对,极化子对经过进一步拆分得到的自由载流子随后被电极提取形成电流。但拆分后生成的自由电子和空穴又会因为非成对极化子的复合作用[21]而重新复合成极化子对,这种非成对极化子复合会造成提取的自由载流子减少,导致提取电流的损失。
为了减少非成对极化子复合带来的电流损耗,一方面要抑制非成对极化子复合,另一方面提高电极对自由载流子的提取能力。钙钛矿和电子(空穴)传输层之间最低未占分子轨道(LUMO)的能级差越大,越有利于提高极化子对拆分的有效性[22],但这会导致器件的开路电压减小。在实际的实验过程中,需要合理选择钙钛矿材料及电子(空穴)传输层的材料以平衡两者之间的关系。通过制作双层电子传输层[23],提高载流子负载能力和增强电子提取能力。Ren等[24]的研究表明,表面非成对极化子复合不会影响退火器件的光电流,故可以采用退火工艺来提高器件性能。
为了对提出的模型进行验证与分析,选取了García-Sánchez等[14]的 实 验 数 据 进 行 模 型 拟 合 分析,同时与Pozo等[13]提出的模型进行对比,图5为比较结果。从图5可以看到,采用的实验数据在第一象限有明显的指数型上升。虽然Pozo等提出的模型可以拟合S型曲线,但是对于第一象限的变化规律只能实现线性表征,而改进模型则可实现对实验数据的有效描述。
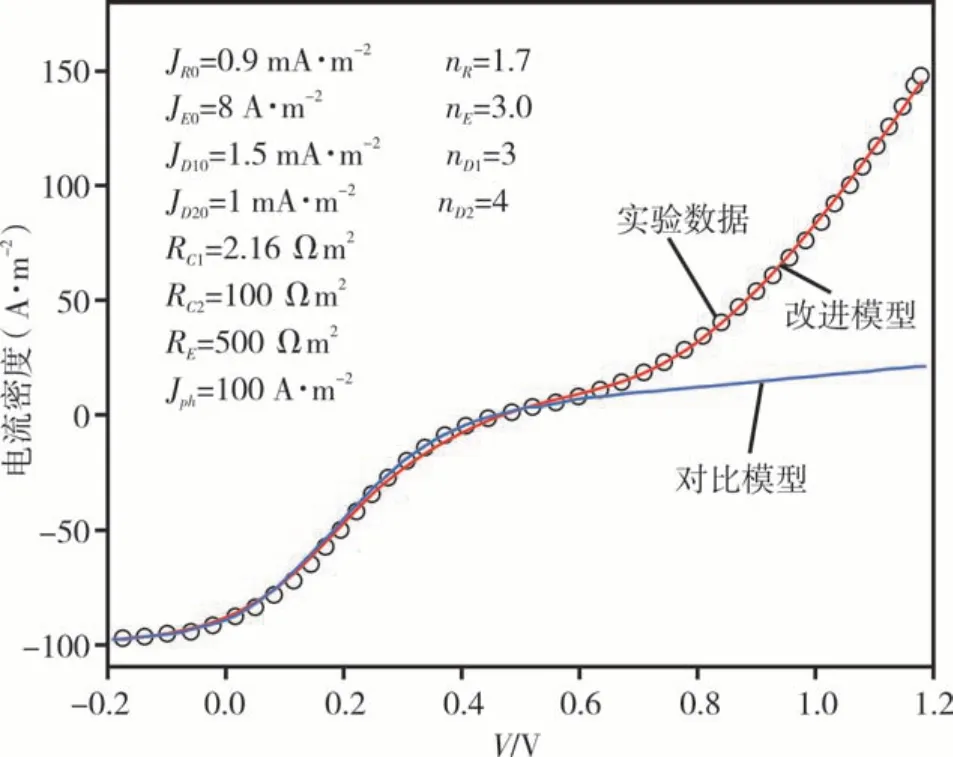
图5 照明条件下太阳能电池的实验测量数据[14]、Pozo模型[13]和改进模型的比较结果Figure 5 Comparisons of experimental solar cell measurement data under lighting conditions,Pozo’s modeland our proposed model
为了进一步检验上述改进模型的有效性,选取一组钙钛矿太阳能电池的实验数据进行验证[25],该太阳能电池的制备使用聚3-己基噻吩(P3HT)作为空穴传输层[26],富勒烯及其衍生物[6,6]-苯基-C60-丁酸异甲酯(PCBM)作为电子传输层[27],并且对透明玻璃基板进行不同时长的氧等离子体处理后,再对电流电压特性进行测量。图6为照明条件下钙钛矿太阳能电池的实验数据与改进模型的拟合结果,而模型参数列于表1。从图6可见,在经不同时长的氧等离子体处理后,电流电压曲线表征出的不同特性,但均能通过改进模型得到良好拟合。实验数据和拟合曲线之间的高度一致性,证明改进模型不仅可以对常规的电流电压曲线仿真,对于特殊的S型曲线也有良好的拟合能力,进一步印证了改进模型的有效性和广泛适用性。

表1 模型拟合参数Table 1 Model fitting parameters

图6 照明条件下钙钛矿太阳能电池的实验数据与改进模型的拟合结果Figure 6 The experimental data of the perovskite solar cell under lighting conditions and the fitting result of the improved model
需要指出,虽然太阳能电池出现S形曲线的具体原因目前仍未知,但基于改进集总参数等效电路模型,实现对该S形实验结果的描述,则是今后其物理机理研究的前提,这也可为高转换效率太阳能电池的工艺制备指明方向。
3 结语
提出了一个改进的集总参数等效电路模型,其可实现对有机/无机杂化钙钛矿太阳能电池电流曲线中指数型上升的实验结果的描述。通过对不同太阳能电池实验数据的交叉验证,表明改进模型有较好的拟合表征能力,同时可获得电流的显式方程。因此,改进模型不仅可以解释其I-V特性中的S形扭结,同时也可作为嵌入光伏系统电路模拟器的有效工具。
