连续催化重整集总模型参数估计效率的优化

2022-07-13杨向文陈夕松

石油炼制与化工 2022年7期

杨向文，陈夕松，杨卫，蒋宇

(1.东南大学自动化学院，南京 210096；2.南京富岛信息工程有限公司)

连续催化重整(简称重整)是炼化企业加工石油的主流工艺之一，主要用于高辛烷值汽油、轻芳烃和氢气的生产，对企业整体经济效益至关重要。对重整过程进行流程模拟，可以优化生产操作，发现过程薄弱环节，有助于提高企业效益。

流程模拟的效果取决于构建模型的精准性，对于重整过程的模拟目前多采用集总模型。构建集总模型，一般先根据反应物分子结构和动力学特性划分集总，建立初始模型；然后对初始模型进行参数估计，并用实验室试验数据或工业生产实际数据修正。虽然模型参数估计有理论方法为依据，但是理论参数估计得到的模型与工业实际生产过程往往存在偏差，因此需要使用实际生产数据对集总模型参数进行修正。

重整反应体系极其复杂，有近300种组分，重整过程中发生的反应更是不计其数[1]。各反应的速率受到反应物浓度、反应压力、反应温度、催化剂活性等诸多因素的影响，反应物间的相互转化存在较强耦合性，不同反应的反应速率也存在较大差异，致使依靠传统算法的梯度求解难度很大。以30个集总为例，若采用传统算法进行一次参数估计得到满意结果，往往需要调用近万次集总模型，参数估计效率很低。因此，优化参数估计算法势在必行。有学者采用变尺度法(BFGS)[2]和Marquardt法[3]等对梯度运算进行优化，但随着集总划分不断精细化，模型愈加复杂，梯度运算仍然难以进行。徐斌等[4]和王建伟等[5]将进化算法和群智能算法等智能算法用于提高参数估计速率，智能算法虽然不依赖梯度计算、速率高，但其往往只专注于算法本身性能的提升，易出现局部最优解和收敛效果不佳等问题。从生产工艺角度分析，集总模型存在偏差主要是因为模型存在刚性[6]。Dotto等[7]优化了刚性微分方程的数值求解算法，采用Gear法对刚性集总模型进行计算，但Gear法需要迭代多次求解，求解效率有待提升。

上述方法均未能彻底解决集总模型的刚性问题和集总模型参数估计效率较低问题，本研究通过深入分析重整生产工艺，采用准稳态假设简化集总模型，在遵循反应真实变化规律的前提下去除集总模型的刚性，在保证模型计算精度的条件下有效提高集总模型参数估计效率，期望高效精准地对重整过程进行流程模拟。

1 集总模型参数估计效率的优化

1.1 重整集总模型建立

建立重整集总模型，首先按结构相似、动力学特性相同的原则，对重整体系中的反应物进行分类，即划分集总[8]，然后将集总作为虚拟的单一组分，建立简化的集总反应网络动力学模型。集总划分越细，模型越精确，计算难度越大，目标函数越难以收敛；集总划分过粗，则会忽视反应物间的性能差异，导致模型精度不足。因此，在保证模型精度的前提下，为简便计算将重整过程中的反应物划分为30个集总，建立30集总反应动力学模型。具体的集总划分为：按照碳数为C1～C12将烷烃划分P1～P12共12个集总；按照碳数为C6～C12将环烷烃划分5N6(甲基环戊烷)、6N6(环己烷)和N7～N12环烷烃共8个集总；按照碳数为C6～C12将芳烃划分A6～A12共10个集总，其中A8包括乙苯(EB)、间二甲苯(PX)、对二甲苯(MX)、邻二甲苯(OX)4个集总。

30集总模型的反应网络如图1所示。由图1可知，30集总模型的反应网络包括了7种烷烃脱氢环化生成环烷烃反应、7种环烷烃脱氢环化生成芳烃反应、6种芳烃氢解反应和20种烷烃加氢裂化反应，共计40种反应。

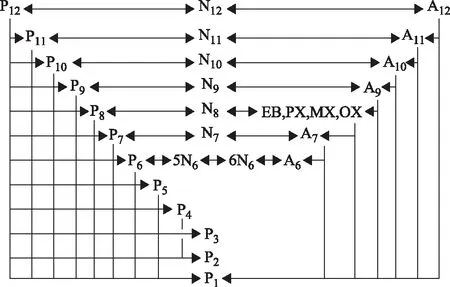
图1 重整体系30集总模型的反应网络

重整过程集总模型的建立使用实验室试验数据进行参数估计，其与工业实际生产情况存在偏差。为使所建模型符合工业实际情况，对模型参数估计的修正归结为求解40个参数修正因子(λj，j=1，2，…，40)。反应动力学中，反应物的浓度变化可以用其在流向不同位置上摩尔流量变化率来描述。30个集总模型中每个集总的摩尔流量变化率常微分方程组(ODE)如式(1)所示。

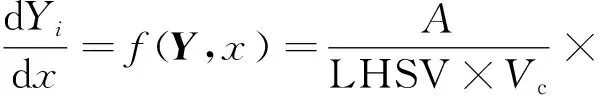
(1)

式(1)中：Yi为集总i的摩尔流量，kmol/h；Y为30个集总摩尔流量集合，Y=(Y1，Y2，…，Y30)；Yi0为集总i在反应器入口的初始摩尔流量，kmol/h；x为相对于反应器外表面的反应物流向坐标，m，如图2所示，反应物从反应器外表面向中心做径向流动；A为反应物流向截面积，m2，对于径向反应器为A=2πxH，其中H为反应器高度，m；Vc为催化剂装填量，m3；LHSV为液时空速，h-1；r+和r-分别为集总i在所有反应中的总生成速率和总消耗速率，kmol/h。

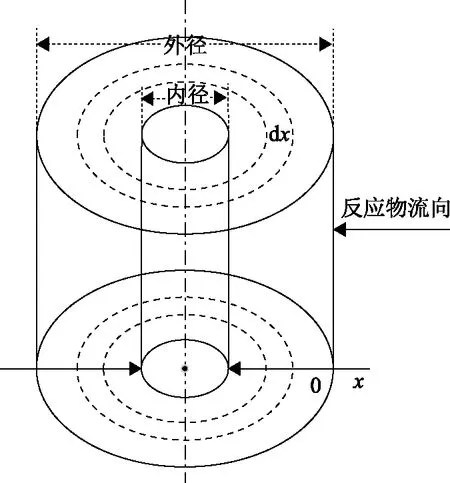
图2 重整反应器中反应物流向示意

可逆反应和不可逆反应的反应速率(r)的计算方法不同。以烷烃脱氢反应为例，可逆反应的反应速率计算如式(2)所示。

r=k×(YPs-YNs/keq)

(2)

以芳烃氢解反应为例，不可逆反应的反应速率计算如式(3)所示。

r=k×YAs

(3)

式(2)和式(3)中：s为碳原子数；YPs为反应物烷烃Ps的摩尔流量，kmol/h；YNs为生成物环烷烃Ns的摩尔流量，kmol/h；YAs为反应物芳烃As的摩尔流量，kmol/h；k为反应速率常数，h-1，keq为可逆反应平衡常数，k和keq的计算如式(4)～式(6)所示。

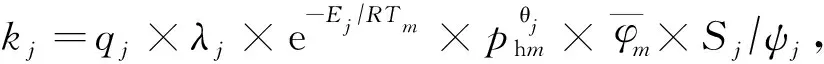
(4)

keqj=e-ΔGmol/RTj；j=1，2，…，40

(5)

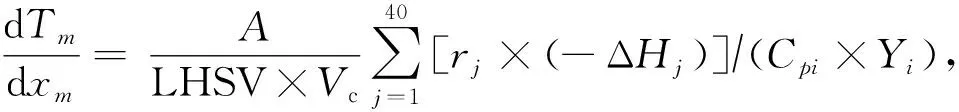
(6)

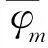
1.2 准稳态假设

1.2.1集总模型中的刚性组分

进行准稳态假设时，需要先找到模型中的刚性组分，然后再进行稳态假设。对于某化学反应体系，刚性组分一般满足式(7)描述特征，即刚性组分为体系中摩尔流量很小但流量变化率很大的组分，一般是不重要的中间产物。

(7)

式中，δ为较小阈值，r+-r-≈0。

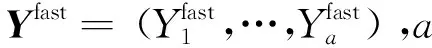
1.2.2准稳态假设

在化学反应过程中，刚性组分的摩尔流量在反应初期变化快，反应后期变化逐渐缓和，直至达到平衡状态[11]；稳态组分的摩尔流量在整个反应过程始终处于动态平衡状态，不会发生较大变化。准稳态假设，即将刚性组分近似看作稳态组分，从而简化计算、去除模型的刚性。

将刚性组分近似作为稳态组分后，其摩尔流量基本不变，即r+-r-=0，则：

(8)

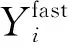
(9)

然后将式(9)代入到集总模型式(1)中，求解其浓度。集总模型从式(1)简化为式(10)，将刚性组分从ODE求解体系中剥离出来，以此降低模型的刚性和求解计算规模。

(10)

将准稳态假设简化的30集总模型与带刚性组分的30集总模型进行对比。首先对比使用ODE求解器获得的两模型中集总摩尔流量的变化曲线，分析准稳态假设模拟集总组分化学动力学特性的准确性；进而对比两个模型的参数估计效率，分析准稳态假设对集总模型参数估计效率的影响。

2 模型验证与分析

2.1 实例验证

利用某炼化企业重整装置的生产数据对集总模型进行实例验证。该重整装置有4个反应器(M=4)，对于每个反应器而言，集总模型结构相同，而模型初始值和反应器参数不同。为避免重复，以第一反应器为例，首先根据式(1)建立30集总模型ODE，然后使用MATLAB中ODE23S刚性求解器对集总模型ODE进行求解，进而用内点法进行模型参数估计，获得第一反应器集总模型中30个集总的摩尔流量变化情况。结果发现，N11和N12集总的摩尔流量变化率明显大于其他集总，与N11和N12有关的化学反应式如式(11)所示。

(11)

从式(11)可以看出，N11为P11转化为A11的中间产物，N12为P12转化为A12的中间产物。集总模型中与N11和N12有关组分的摩尔流量变化曲线如图3所示。由图3可见：反应初期，相较于P11和A11，反应物流向坐标小于0.05 m时，N11摩尔流量急剧增大，其变化曲线的斜率极大，但是其摩尔流量比P11和A11的摩尔流量小1～2个数量级；而反应后期(流向坐标大于0.2 m)，N11和N12摩尔流量变化曲线的斜率逐渐减小，摩尔流量趋于稳定。N11和N12摩尔流量的变化情况符合刚性组分的变化特征，即N11和N12为集总模型中的刚性组分。因此，将N11和N12近似看作稳态组分，进行准稳态假设简化。

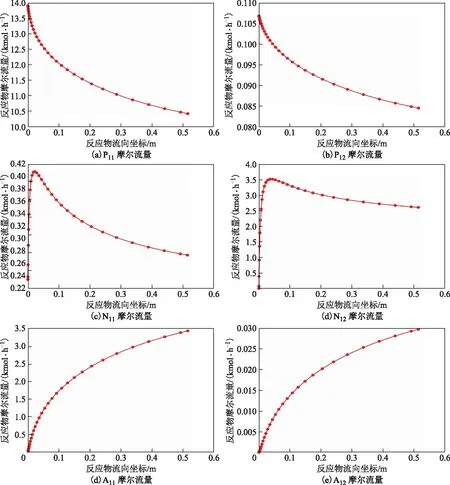
图3 P11，N11，A11，P12，N12，A12组分的摩尔流量变化曲线

根据式(1)和式(2)，集总组分N11和N12的净生成速率分别由式(12)和式(13)计算。

(12)

(13)

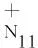
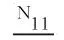
(14)

(15)

将式(14)和式(15)代入30集总简化模型式(10)中求解。这样就不再需要求解刚性组分N11和N12的摩尔流量，从而降低了模型的刚性，进而采用非刚性求解器ODE23对集总模型进行更快地求解和参数估计。准稳态假设前后P11，N11，A11，P12，N12，A12摩尔流量的变化曲线如图4所示。

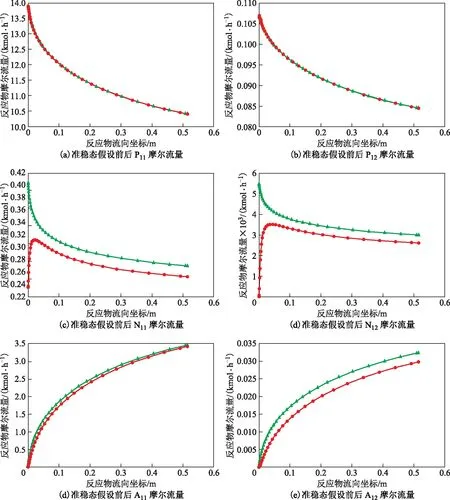
图4 准稳态假设前后P11，N11，A11，P12，N12，A12的摩尔流量变化曲线对比●—原始曲线; ▲—准稳态假设曲线

由图4可见：采用准稳态假设后，P11和P12摩尔流量的变化曲线与准稳态假设前一致；而N11，N12，A11，A12摩尔流量的变化趋势不变，但与准稳态假设前存在一定偏差。这表明，采用准稳态假设较好地保持了原始集总组分的化学动力学特性，符合反应中组分摩尔流量的真实变化情况。准稳态假设后组分摩尔流量变化曲线中的偏差被称为QSSA瞬时误差，该误差代表了计算准稳态组分摩尔流量时存在的连续扰动[12]。反应过程中，P11和P12先转化为N11和N12再转化为A11和A12。P11和P12在这6个集总中为原料集总，因此P11和P12流量计算并未受到准稳态假设后N11和N12摩尔流量计算偏差的影响；而A11和A12在这6个集总中为产物集总，其摩尔流量的计算直接受到N11和N12摩尔流量计算偏差的影响，导致其变化曲线存在一定偏差。

2.2 模型参数估计

采用准稳态假设去除模型刚性组分后，对简化模型进行参数估计，并与含刚性组分的30集总模型的参数估计效率进行对比。模型参数估计时，设定决策变量为40个模型参数修正因子(λi)，设定目标函数为理论模型中的摩尔流量、温度等参数与实际情况差值的加权总和。目标函数的最小值为：

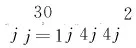
(16)

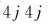
准稳态假设前后集总模型参数估计的目标函数变化曲线如图5所示，为更清晰地展示目标函数的变化情况，对目标函数取对数表征。准稳态假设前后集总模型参数估计的指标如表1所示。

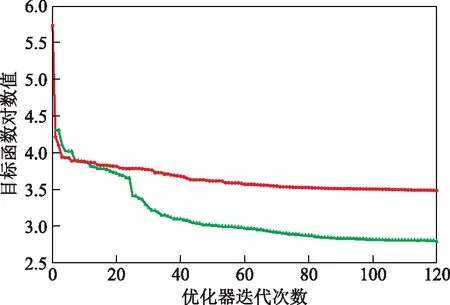
图5 准稳态假设前后模型参数估计的目标函数变化 —原始模型； —准稳态假设简化模型

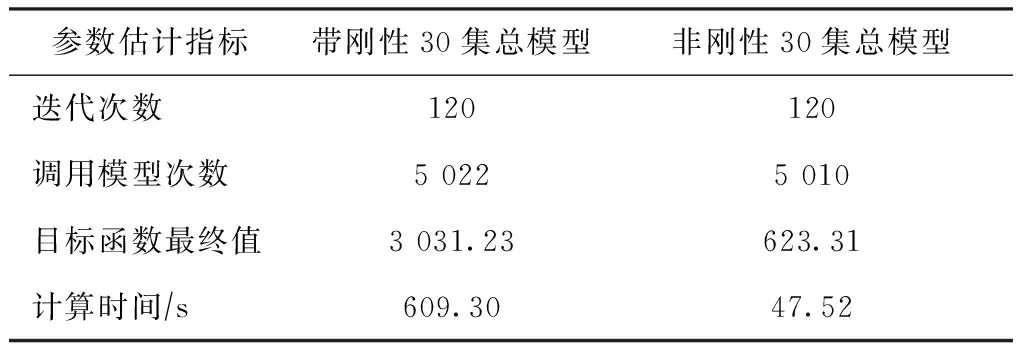
表1 准稳态假设前后集总模型参数估计的指标

从图5和表1可见：与带刚性的30集总模型相比，采用准稳态假设简化去除了集总模型的刚性，模型参数估计的计算速率提升了约10倍，估计效率得到显著提高；而且，由于去除了模型的刚性组分，减小了集总组分之间摩尔流量变化率的差异，目标函数迭代计算的最终值大幅减小，说明简化模型计算结果与实际情况的一致性比刚性模型大幅提高；同时，在基本不损失模型计算精度的情况下，简化集总模型更易拟合，目标函数的收敛更加迅速，有效提升了模型参数估计的效率。

综上所述，采用准稳态假设后，虽然刚性组分及部分非刚性产物组分的摩尔流量计算出现一定偏差，但各组分的摩尔流量仍保持了原来的变化趋势，符合实际情况；而且，采用准稳态假设后模型参数估计的效率得到大幅提升，较小的计算精度损失是可接受的。