姿态变换护理机器人的轨迹规划与仿真

董文超,张争艳，马 聪，王厚程

(1.河北工业大学 机械工程学院， 天津 300401；2.国家技术创新方法与实施工具工程技术研究中心， 天津 300401)

0 引言

脑卒中是严重危害中国国民健康的重大慢性疾病，具备高发病率、高致残率的特点。患者会留下不同程度的后遗症，如偏瘫、截瘫等，随着患者数量逐渐增多，导致医护人员严重短缺，促进了护理机器人的发展[1-2]，护理机器人在专业要求较高的康复治疗中具有广泛的应用前景。因此，开发先进的护理机器人具有重要意义。

现有护理机器人主要分为双臂移乘式护理机器人[3-4]、外骨骼穿戴式护理机器人[5-6]、床椅分离式护理机器人[7-10]和多功能变形式轮椅[11-12]。双臂移乘式护理机器人自由度较高，能够辅助被护理人实现不同生活器具之间的转移和大部分简单的护理任务，但舒适性与安全性还需提升；外骨骼穿戴式护理机器人可以提供额外能量来供被护理人四肢运动，逐步恢复腿部的行走功能，但很难做到智能穿脱，人机系统的步态规划和控制还不够智能，很难得到应用；床椅分离式护理机器人虽具有护理空间大、安全性高等优势，但存在机械结构复杂、占用空间大、重量大等缺点，灵活性较差；多功能变形轮椅结构紧凑、安全性高、占用空间小、灵活实用、适用范围广，既可以作为代步工具又可以对使用者进行姿态变换训练，具有广阔的发展空间和市场应用前景。

护理机器人服务对象是身体机能下降的老年人及下肢功能障碍患者，需要减小运动的冲击惯性并保障舒适性，故需要对护理机器人进行运动轨迹规划。机器人轨迹规划的方法主要包括笛卡尔空间轨迹规划和关节空间轨迹规划算法[13]。金荣玉等[14]提出一种基于组合函数的笛卡尔轨迹规划方法，该方法能够解决笛卡尔空间轨迹规划遇到动力学奇异，造成轨迹规划失效的现象。刘玉鑫等[15]提出了一种通过人背人试验设计机器人运动轨迹的轨迹规划方法，该方法提高了被护理人在移乘过程中的舒适性。马睿等[16]提出了一种基于遗传算法的三次多项式插值最短时间轨迹优化算法，该算法提高了轨迹规划的科学性、实用性与可行性。Chembuly等[17]基于机器人结合运动学、动力学并利用五次多项式插值进行关节轨迹规划，仿真结果表明该联合轨迹的结果是平滑和高效的。Kim等[18]提出了一种基于 Catmull-Rom样条的轨迹规划算法，该算法允许机器人通过任务空间中的几个路径点，仿真结果表明与三次样条轨迹规划相比，该轨迹规划算法所需计算量更少。Dupac[19]提出了一种基于笛卡尔与极坐标分段三次插值相结合的轨迹规划算法，该算法可以轻松计算运动学变量和生成平滑的运动轨迹。

本文基于一种新型多姿态变换机器人的结构设计，对机器人的运动轨迹进行轨迹规划较为复杂，低阶多项式插值不能满足需要，故运用关节空间轨迹规划算法中的五次多项式插值法(五次多项式插值法可以在开始和结束时控制关节运动的速度和加速度，保证护理机器人运动的平稳性)对姿态变换机器人坐站变换与坐躺变换2个运动过程进行运动轨迹规划，依靠电动推杆与丝杠滑台2个驱动间的配合，实现坐-躺-站3种姿态间的平稳转换，建立姿态变换机器人的虚拟样机并进行运动轨迹仿真，最后制作了机器人样机并进行了机器人的空乘实验与负载试验，证明设计的运动轨迹在机器人运动周期内平稳可靠。

1 机器人姿态变换运动学分析

下面进行机器人坐姿-躺姿变换与坐姿-站姿变换的运动学分析，为了便于分析，将靠背和电动推杆同时处于竖直位置时，H点所在位置作为原点O，建立坐标系，图1为机器人机构示意图，图2为机器人三维模型示意图，表1为运动学公式中的参数符号说明。

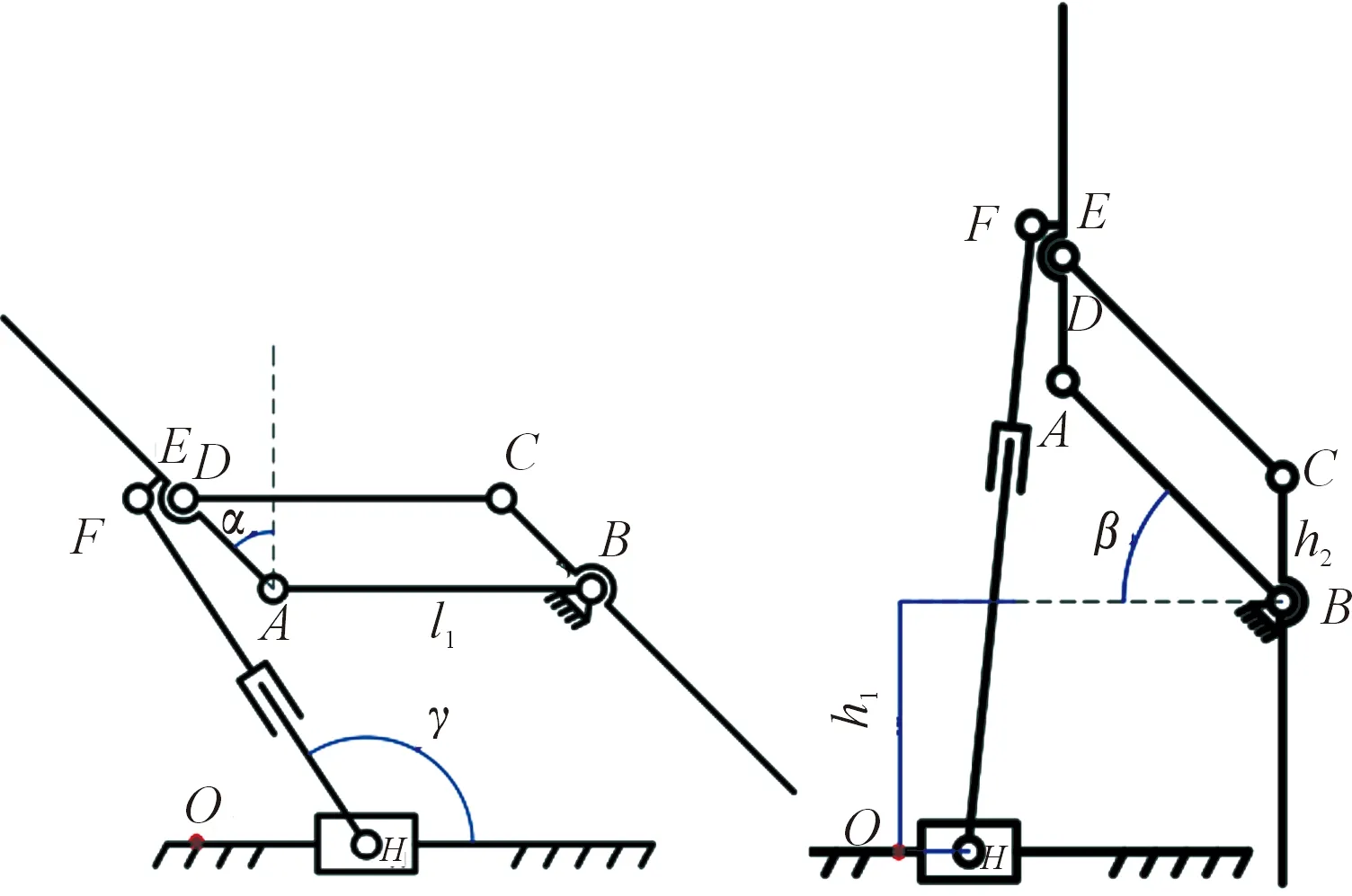
图1 机器人机构示意图

图2 机器人三维模型示意图

表1 机构参数符号

(1)

(2)

式中，h1=425 mm，h2=200 mm，l1=500 mm，l2=50 mm，l3=206 mm，θ=14.036°。

式(1)与式(2)中的s和x与电动推杆和丝杠滑台有关，通过两驱动的设置便于对机器人的运动进行实时监控。s和x都是关于时间t的函数，故靠背转角α和座板转角β对t分别求一次导和两次导就可以得到两转角的角速度与角加速度。

2 机器人轨迹规划

2.1 关节运动规划

关节轨迹规划是指确定关节角度在初始位置和终止位置之间所经过路径，以及经过各路径点的速度、加速度等[20-21]。由于机器人平行四边形的结构设计，被护理人由坐到站的过程中背部会随着背板一直保持竖直的状态完成站立，故由坐到站只需规划座板转角β的运动轨迹即可；被护理人由坐到躺的过程中，腿板与背板保持平行，故只需规划靠背转角α的运动轨迹即可。姿态变换护理机器人的工作状态如图3所示，机器人辅助人体姿态变换轨迹如图4所示。

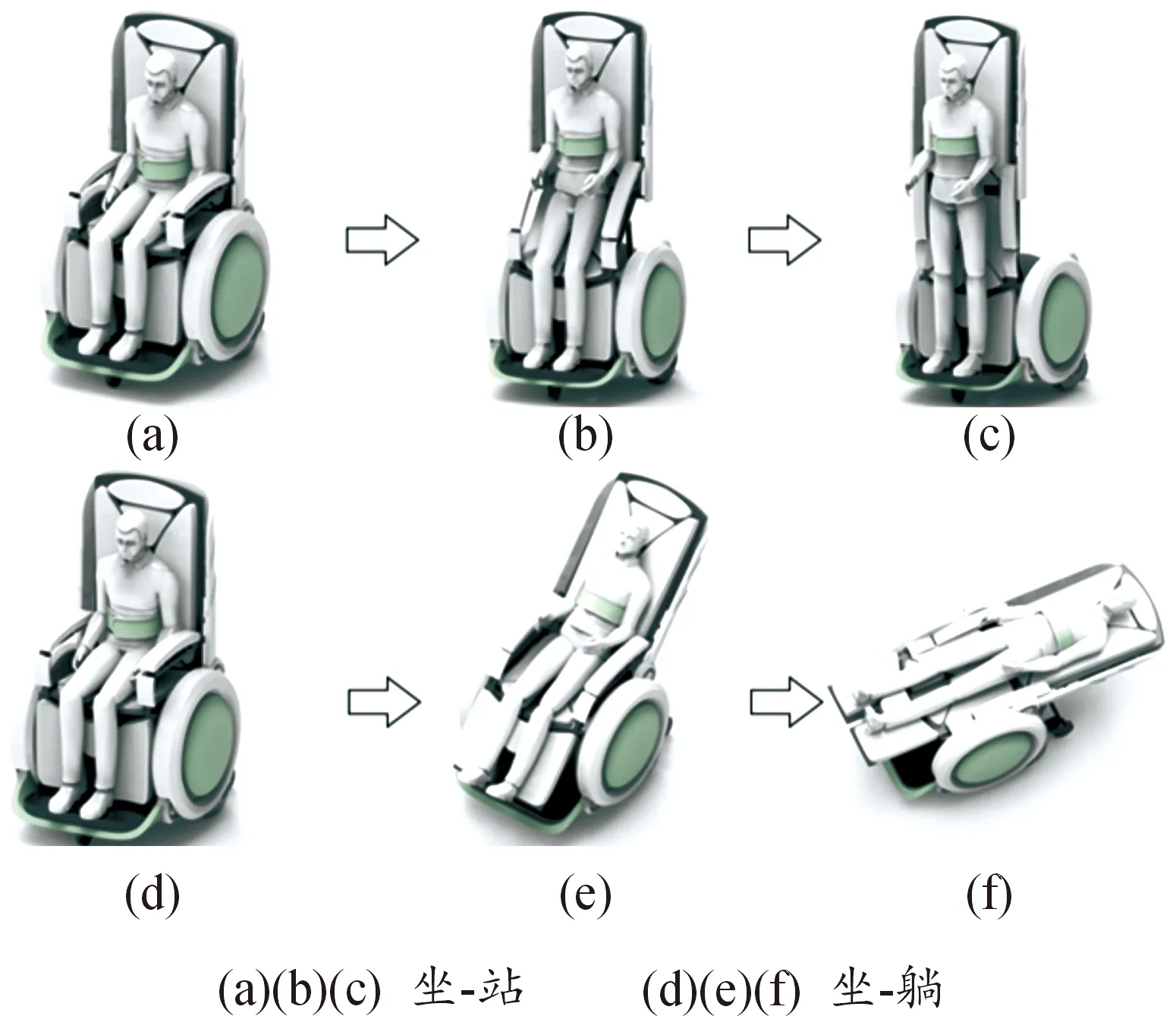
图3 机器人工作状态示意图

图4 机器人辅助人体姿态变换轨迹

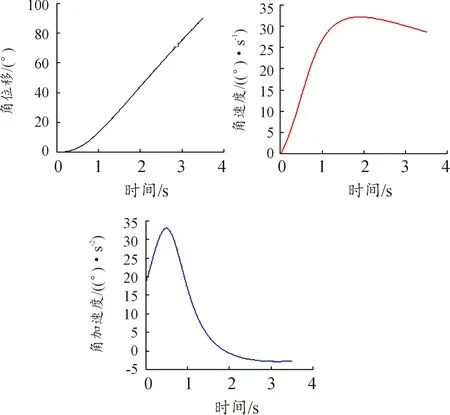
图5 机器人坐躺轨迹曲线

根据文献研究反馈，协助坐站转换(STS)时间超过7 s，受试者会产生缓慢与不舒服的感觉，然而，当辅助STS时间少于3 s时，受试者又很难完成起立动作[22]，故4～6 s为起立的舒适区间，为了避免辅助起立过快导致被护理人二次受伤，选择舒适区间的最大值6 s为辅助起立时间。用线性函数对姿态变换机器人进行轨迹规划，设定满足坐-站功能的驱动函数x=166.67t-500(3≤t≤6)(mm)，s=625+83.33t(0≤t≤6)(mm)，座板转角β的角位移、角速度、角加速度，如图6所示。

由图6可以发现机器人在工作过程中会出现震荡以及速度、加速度突变等情况，有必要进行轨迹优化。

图6 机器人坐-站轨迹曲线

2.2 五次多项式插值法进行机器人轨迹优化

由上节可以发现利用线性函数对姿态变换机器人进行轨迹规划能够满足机器人工作要求，但会给被护理人带来不适的感觉。运用关节空间轨迹规划算法中的多项式插值法对姿态变换机器人坐站变换与坐躺变换2个运动过程进行运动轨迹规划。多项式插值法就是利用多项式函数来生成轨迹曲线[23]，多项式函数的各项系数的求取是以关节角运动的约束条件为已知条件[24]。在多项式插值法中常用到三次多项式插值法与五次多项式插值法。三次多项式插值法仅限制了初始时刻和最终时刻的位置与速度，不能指定加速度，但是也正是由于不能对机器人加速度进行指定，使机器人的关节加速度在某一时刻可能产生突变，导致机器人产生剧烈震动影响轨迹曲线精度(三次插值多项式的速度曲线均为抛物线，相应的加速度曲线均为直线[25])。由于本文的研究对象为护理机器人，需要保证被护理人的安全，三次多项式插值法不可取。为避免机器人的关节运动轨迹出现超调与波动，保证被护理人的安全，运用五次多项式插值法对机器人的关节运动进行轨迹规划。五次多项式插值法与三次多项式插值法相比，对于计算机处理器要求较高，但是由于加入了对关节加速度的控制，可以提高机器人轨迹的准确性，保证护理机器人运行的平稳性。

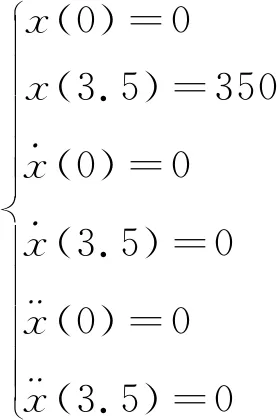
(3)

确定了一个五次多项式

x(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5

(4)

对式(4)求1阶导和2阶导，即可得到机器人的角速度和角加速度

(5)

(6)

将式(3)代入式(4)(5)(6)，即可求得

(7)

确定丝杠的驱动函数：

x(t)=81.632 7t3-34.985 4t4+3.998 3t5

(8)

将式(8)代入式(1)中，可求得靠背转角α的运动轨迹，α对t求1阶导数、2阶导数得到靠背转角α的角位移、角速度、角加速度随时间变化曲线，如图7所示。

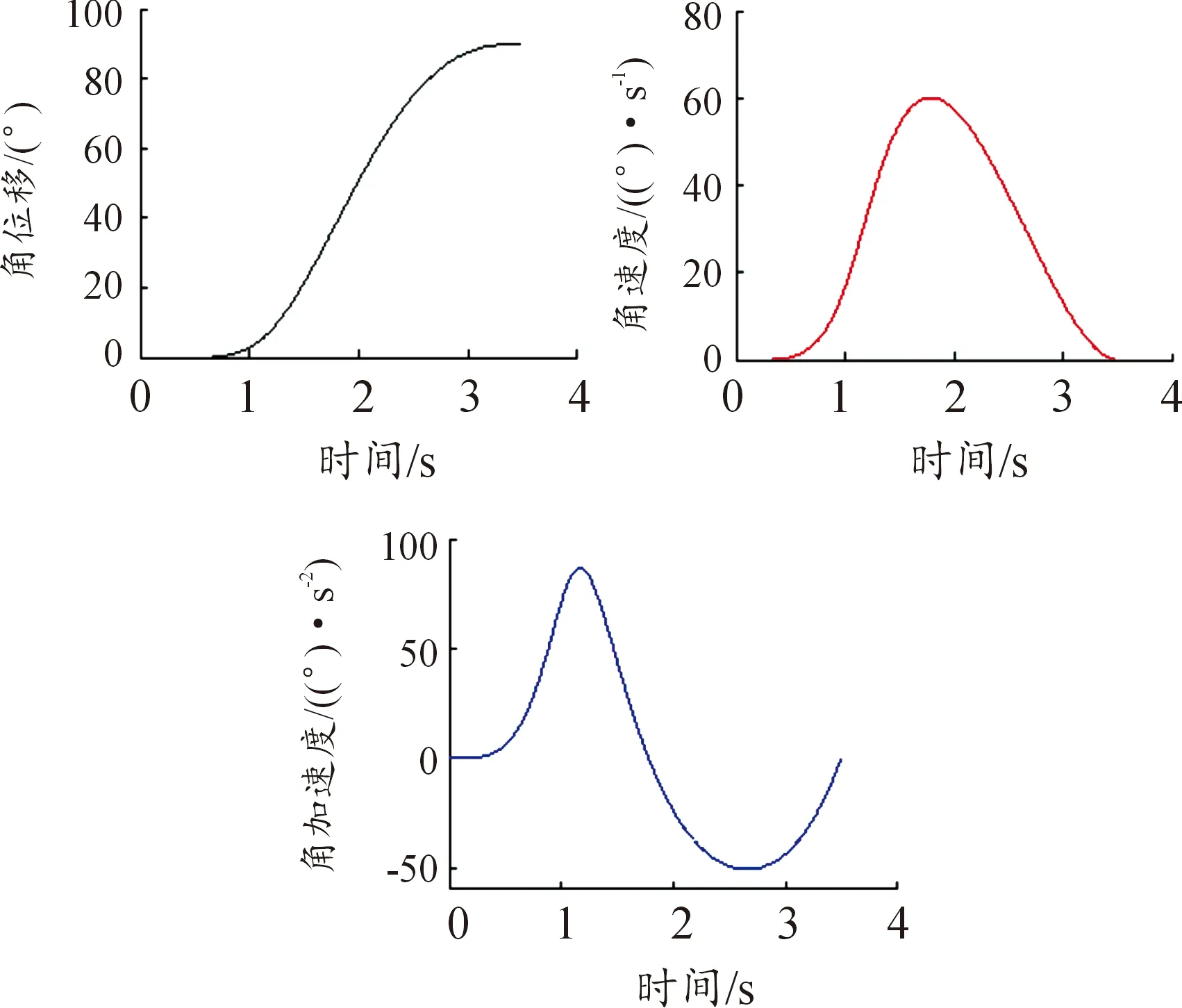
图7 靠背转角α的角位移、角速度、角加速度曲线

根据前文分析辅助患者起立的时间为6 s，同时，机器人在起始和终止的位置座板转角β分别为0°与90°，关节运动速度和加速度为0。给定的约束条件：

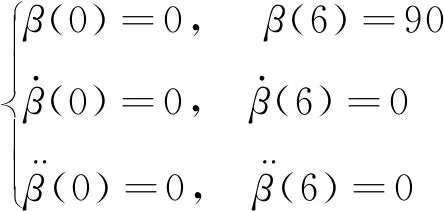
(9)

确定机器人座板转角β的运动轨迹：

β(t)=4.166 7t3-1.041 7t4+0.069 4t5

(10)

对式(10)求1阶导数、2阶导数，绘制座板转角β的角位移、角速度、角加速度随时间变化曲线，如图8所示。

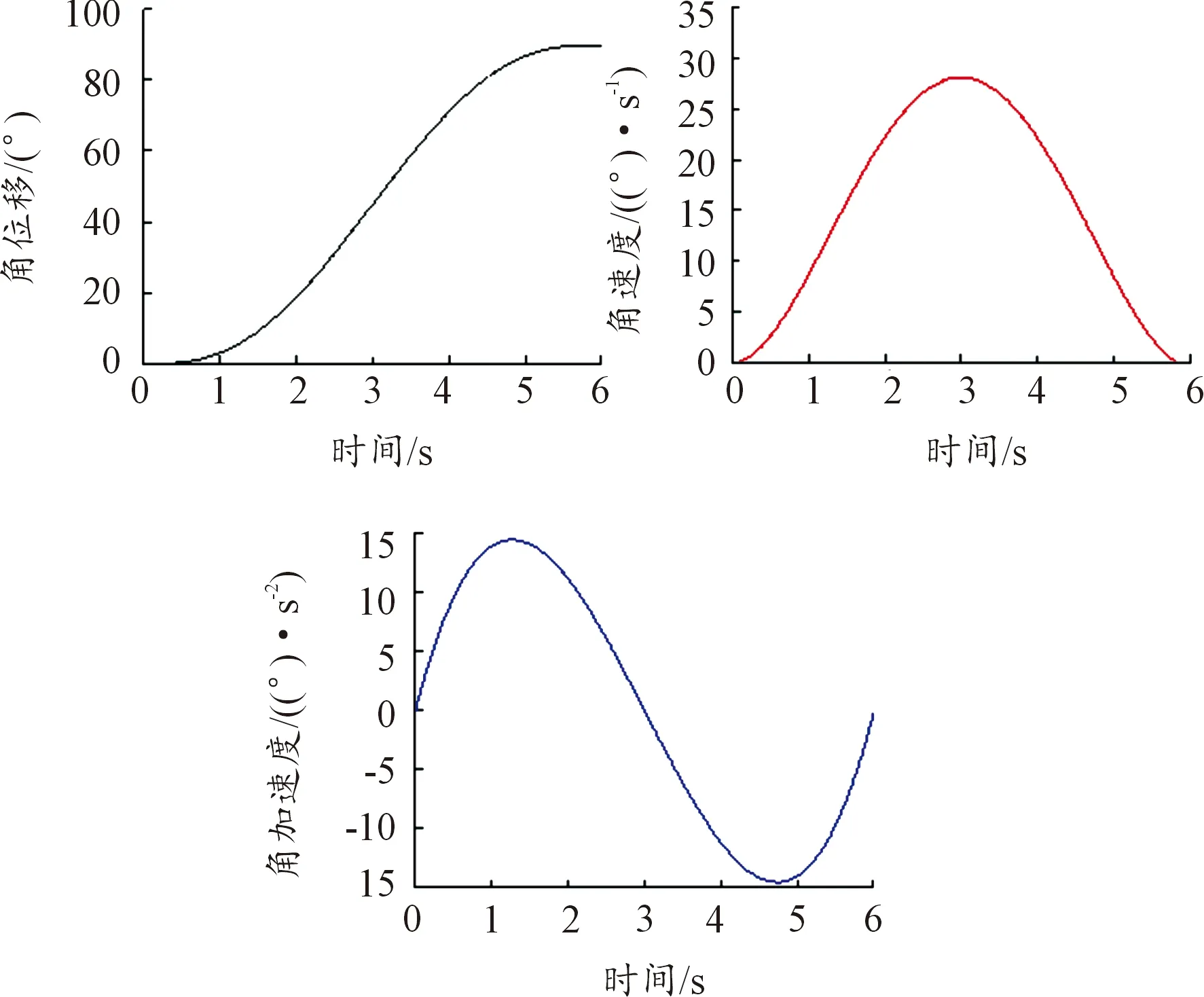
图8 座板转角β的角位移、角速度、角加速度曲线

2.2.3过路径点的五次多项式插值

图9 座板转角β的路径点

从β0到βy的插值五次多项式为

β(t)=a10+a11t+a12t2+a13t3+

a14t4+a15t5

(11)

从βy到β1的插值五次多项式为

β(t)=a20+a21t+a22t2+a23t3+

a24t4+a25t5

(12)

时间区间为[0，t1]与[0，t2]。起始和终止时刻角速度、角加速度为0，路径点的角速度、角加速度已知，给定约束：

(13)

2.2.4机器人一个运动周期内的运动轨迹

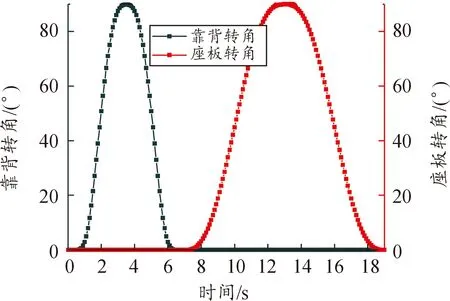
图10 机器人在一个运动周期内的运动轨迹曲线

3 虚拟样机仿真

3.1 建立ADAMS虚拟样机模型

本文首先通过SolidWorks对姿态变换机器人进行建模，之后将SolidWorks模型简化并保存成Parasolid格式导入到ADAMS/View中[26]。在ADAMS中定义各个构件之间的配合关系，运动副类型如表2所示。为移动副Joint8、Joint9施加平移驱动，完成ADAMS虚拟样机建立，如图11所示。

表2 运动副类型

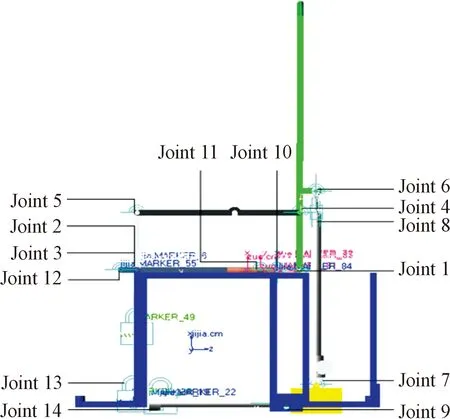
图11 ADAMS虚拟样机示意图

3.2 机器人运动学仿真

图12 坐躺虚拟样机示意图

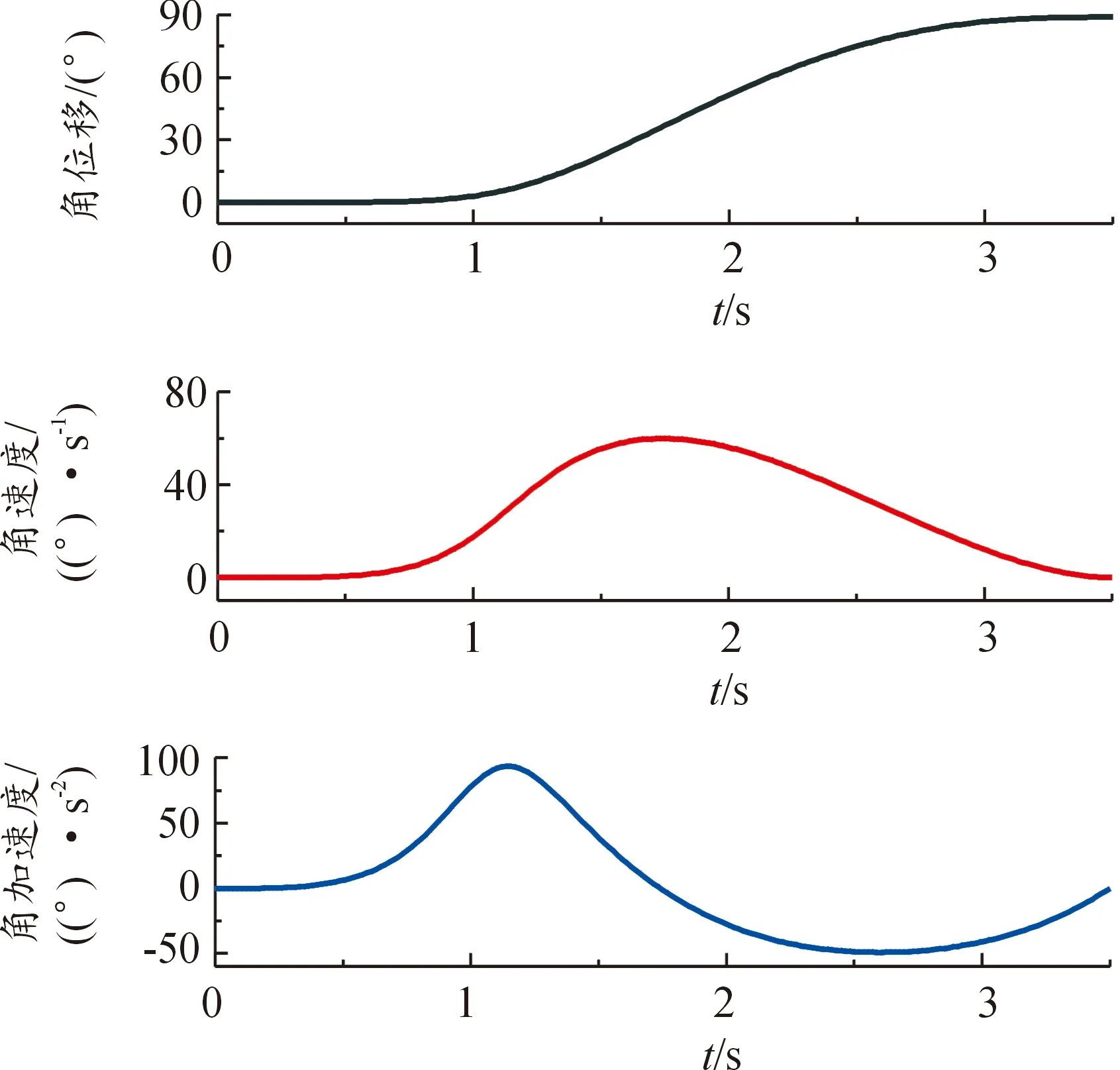
图13 靠背转角α的角位移、角速度、角加速度仿真曲线

(14)

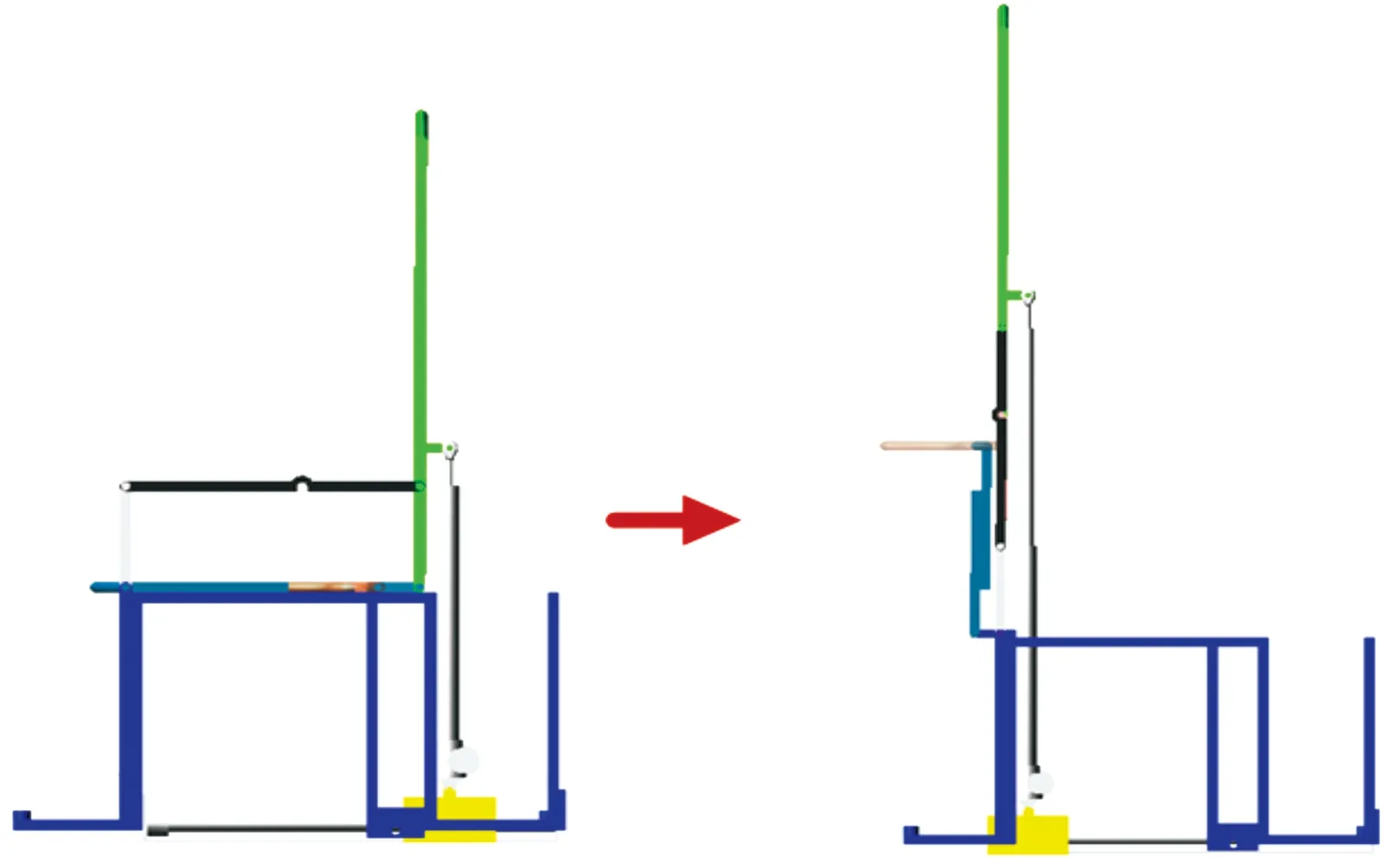
图14 坐站虚拟样机示意图

对比图7与图13以及图8与图15，可以发现它们的变化趋势是一致的，虚拟样机的运动平稳、合理，证明了运用五次多项式插值法进行姿态变换机器人轨迹优化的可行性。接下来可以利用姿态变换机器人仿真样机，测得机器人在运动过程中电动推杆与丝杠的受力变化、各部件间铰接点的受力以及各部件的质心位移，为后续的优化和其他方面的深入研究奠定基础。

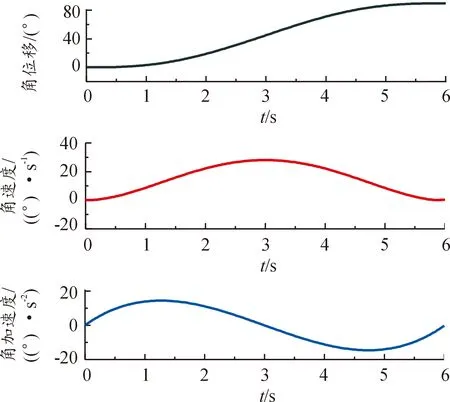
图15 座板转角β的角位移、角速度、角加速度仿真曲线

4 机器人实验

机器人样机包括机器人本体、运动控制卡、驱动器以及上位机。上位机设定驱动器元件的输出值，运动控制卡控制电动推杆与丝杠滑台2个驱动器运动，驱动器驱动机器人关节运动，从而实现机器人的运动。机器人运动过程如图16所示。

图16 机器人运动过程示意图

图17、图18为机器人负载实验，实验表明机器人样机能够辅助被护理人完成坐站变换与坐躺变换。选取5名身高体重不同的实验对象，分别进行机器人辅助姿态变换实验。将实验对象的感受分为4个等级：1舒适、2一般舒适、3一般、4不舒适，机器人轨迹优化前后实验结果如表3所示。

图17 样机坐姿躺姿切换场景图

图18 样机坐姿站姿切换场景图

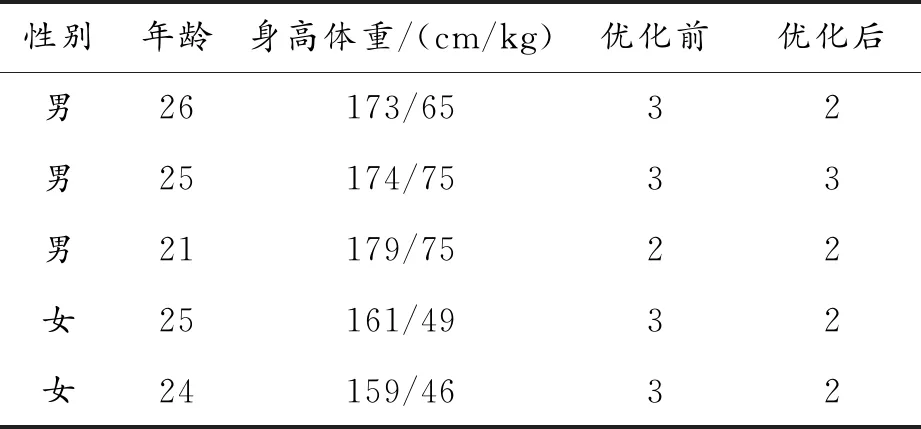
表3 轨迹优化前后舒适性分析

询问受试者的实验感受，大部分人认为未进行轨迹规划时，机器人在运动过程中会出现速度不稳定的现象，停止时没有缓冲，舒适性一般；轨迹优化后，机器人在开始运动和终止运动前速度缓慢，在运动过程中速度平稳，达到了一般舒适。

5 结论