一类非线性系统的自适应抗测量噪声的输出反馈镇定

林 雷,沈艳军

(三峡大学电气与新能源学院,湖北宜昌 443002)

1 Introduction

The problem of stabilization has been well studied for nonlinear systems via output feedback in the past few decades.Most of the results are derived under the condition that the output can be measured precisely [1-4].However,since the influence of disturbance or sensor error,sometimes,we cannot get the accurate values of the output.For this reason,the synthesis problem has been studied for nonlinear systems with output containing disturbance,such asy=x1+ρ,whereρdenotes disturbance.For instance,an adaptation-gain observer was designed for a class of nonlinear systems with measurement noises [5].The authors in [6]addressed anL1adaptive output-feedback descriptor for multi-variable nonlinear systems with measurement disturbances.

However,sometimes the error in the output is not related to time,but related to the states.Therefore,researchers proposed the assumptiony=φ(x1) [7-9],whereφ(·)is a function with respect tox1.In order to stabilize this type of systems,it is usually needed to assume thatyis differentiable.For example,the authors in[8]studied output feedback stabilization for uncertain nonlinear systems with unknown growth rate and unknown output function.A design method was proposed to solve the problem of sampled-data output feedback stabilization for nonlinear systems with unknown output function[9].

Recently,a new output function error model likey=θ(t)x1has been proposed,whereθ(t) is a function with respect to time.Compared with the previous model,it is not necessary to assume that the functionyis derivable when considering the stabilization problem for this kind of nonlinear systems.In fact,it is only assumed thatθ(t) is a bounded function [10-12].The authors in[10]proposed a dual-domination approach to copy with the problem of output-feedback stabilization for nonlinear systems with unknown measurement sensitivity.More specifically,in[11],the authors developed a new stochastic adaptive dual-domination approach to deal with the problem of stabilization for stochastic strict-feedback systems with sensor uncertainty.A large bound of measurement sensitivity was allowed to achieve the regulation of nonlinear systems with unknown growth constant rate [12].However,in practice,nonlinear systems with time-varying growth rate are usually applied to model the circuits with nonlinear resistance[13-14]and business cycles[15].Therefore,it is interesting to research the problem of antimeasurement-disturbance output feedback stabilization for a class of nonlinear systems with multiplicative noises and with time-varying,time-delay growth rate.

In this paper,we study the problem of output feedback stabilization for nonlinear systems with unknown measurement sensitivity.The growth rate of the nonlinear terms has an unknown constant multiplied by a power function of the output and a power function of the output with time delay.Firstly,we present a matrix inequality.Then,based on this matrix inequality,an output feedback controller is constructed with three timevarying gains to stabilize the nonlinear system.At last,a Lyapunov-Krasovskii functional is proposed and sufficient conditions are derived to ensure that the closedloop system is asymptotically stable.Our major contributions include: 1) A useful matrix inequality is proposed.2) Compared with the results in [16-17],the boundedness of the measurement disturbancesθ(t) is enlarged as 0＜θ(t)＜+∞,and the growth rate of the nonlinear terms is time-varying and dependent on the output.

The remainder of this paper is organized as follows.In Section 2,we present some useful lemmas and problem description.In Section 3,an output feedback controller is designed based on a specially constructed observer and three time-varying gains.In Section 4,we give our main results:sufficient conditions are proposed to ensure asymptotical stability of the closed-loop system.Numerical simulations are provided to illustrate the validity of the proposed design methods in Section 5.This paper is concluded in Section 6.

2 Preliminaries and problem description

In this paper,we consider ann-order (n≥ 2)single-input single-output (SISO) uncertain nonlinear system

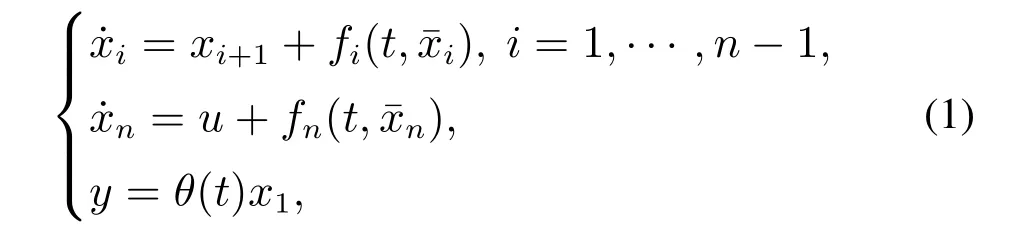
Assumption 1[3,18]There exists a known real numberp≥0 and an unknown constantc ＞0 such that

Remark 1Different from [11-12],the growth rate is a time-varying function in this paper.Whenp=0,the time-varying growth rate is reduced to a constant growth rate.Therefore,the constant growth rate can be regarded as a special case of the time-varying growth rate.Moreover,unlike [10,17],the constantcof the growth rate is unknown.With the introduction of unknown constant,time-delay and sensor sensitivity,it is more difficult to design a stabilizer for the nonlinear system(1).

Remark 2In practice,the nonlinear system with time-varying growth rate satisfied Assumption 1 is usually applied to model the circuits with nonlinear resistance[13-14]and business cycles[15].The dynamical equation called the forced van der Pol equation[19-20]is given as follows:

whereμis an unknown constant.The authors in [20]discussed in detail how an actual nonlinear RLC series circuit was transformed into the equation(2).

Suppose that onlyϑis measurable.Under the coordinate transformationx1=ϑ,x2=,we have

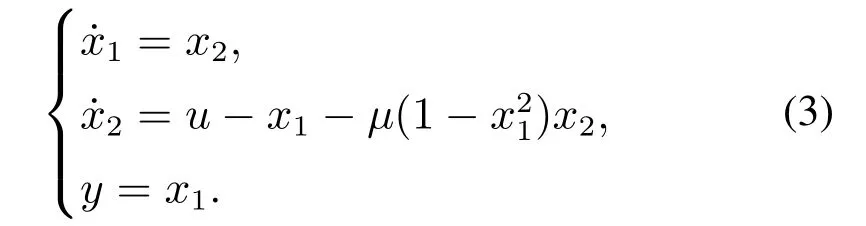
If letc=max{1,|μ|},p=2,then the condition in Assumption 1 holds.Thus,the system(3)has the form of the system(1).

Assumption 2As in[12],the sensor sensitivityθ(t)is assumed to be unknown,continuous and bounded.Moreover,there exists positive constants 0＜θl≤1 and 1＜θu≤∞such thatθl≤θ(t) ≤θu,for allt≥0.

Remark 3In this paper,θ(t) is assumed to be an unknown continuous function with known upper and lower bounds,but does not need to be derivable.In fact,there always exists a multiplicative noiseθ(t).For instance,in[21],the authors pointed out that the magnetic displacement sensor of the bearing suspension system has a sensor error of±10%,which meansθ(t) is a bounded time-varying function ranging from 0.9 to 1.1.Because of its unique properties,it has been widely studied[10-12,16].

Compared with[11,16],in this paper,the allowable measurement error range is enlarged from 0 to +∞.Thus,the proposed method can be applied to nonlinear systems not only with a multiplicative noiseθ(t)close to 1,but also with a multiplicative noise in the interval(0,+∞).

We also need the following inequalities to derive our main results.

Lemma 1[22]For (x y)T∈R2,the following Young’s inequality holds:

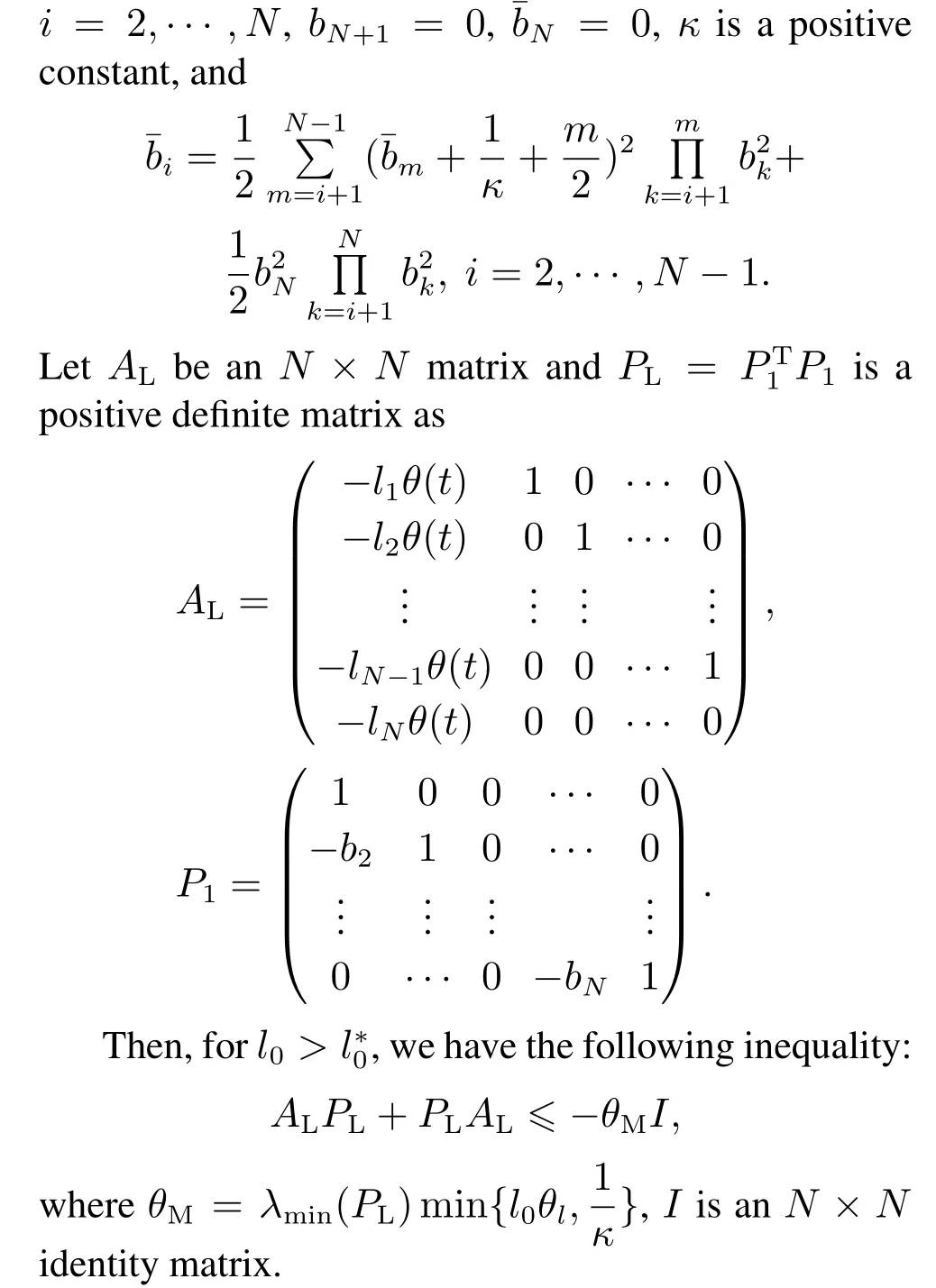
Remark 4The different between Lemma 3 and Lemma 1 in[12]is that a parameterκis introduced.But the proof process is similar and is omitted here.This parameterκcan bring flexibility when designing the output feedback stabilizer.

Lemma 4Suppose that the conditions of Lemma 3 hold.For anN ×NmatrixD=diag{σ,1+σ,···,N -1+σ},there exists an appropriate positive constantσ*,such that whenσ ＞σ*,we have the following matrix inequality:

Remark 5Note thatσ*increases with the increase ofbk.We can select a larger value ofκto makebkandσ*small.For example,whenN=2,κ=10,we haveb2=1.1.Chooseσ=0.25,thenDPL+PLD ＞0.If we chooseκ=1 like[12],whenN=2,we haveb2=2.With the same parameterσ=0.25,we getλmin(DPL+PLD)＜0.

3 Output feedback controller design

In this section,an output feedback controller is constructed for the nonlinear system(1)with unknown sensor sensitivityθ(t) and the time-varying growth rate shown in Assumption 1.

Firstly,construct the following observer:

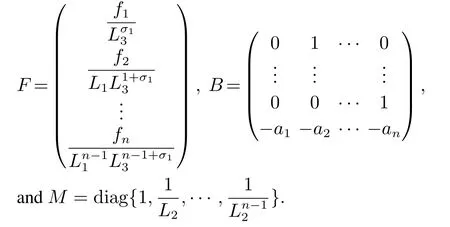
Then,by Lemma 1 in [24],there exists a positive definite matrixQsatisfying

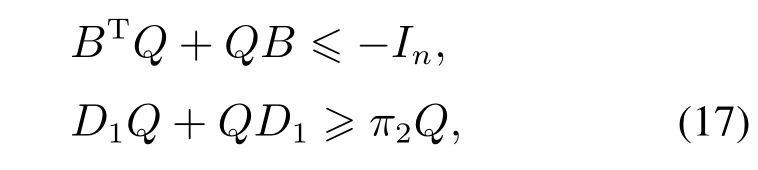
whereπ2＞0 is a real constant.

4 Main results

In this section,we construct a Lypunov-Krasovskii functional to derive sufficient conditions to guarantee that the closed-loop system(15)-(16)is asymptotically stable.

Theorem 1For the system(1)with the Assumptions 1 and 2,if the parametersα,β,σ1,psatisfy the conditions (8)-(11),then,under the output feedback controller(4)-(7),and(12),the system(1)converges to the equilibrium at origin,which means that

ProofThe derivative of the functionV1(t)=eTPLeis given by

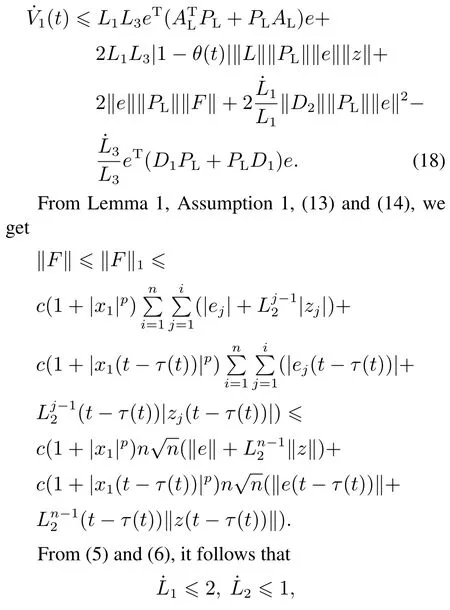
Note that|1-θ(t)|,θ(t)are bounded andc1,c2are two positive constants.The rest proof will be discussed on the following two cases.

Secondly,we proceed our discussion on Case 2.

From (29),we know that whateverL1(t) orL2(t)is bounded,the other is also bounded.

According to(6),we have

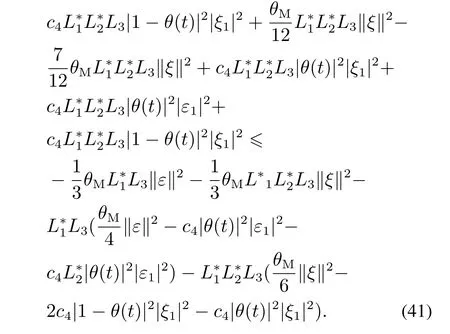
Note that|θ(t)|,|1-θ(t)|are bounded.There exist appropriate positive constantsC3,C4,C5such that(41)can be rewritten as

5 Numerical simulations

In this section,we use two simulation examples to demonstrate the effectiveness of our adaptive antimeasurement-disturbance controller design for nonlinear systems with time-varying,time-delay growth rate.In addition,the third example is applied to compare the performance of our method with the method proposed in[12].

Example 1Consider the following SISO nonlinear system(3)with sensor uncertainty:

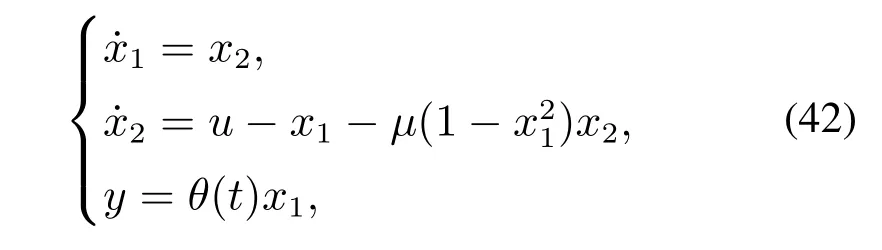
whereμis an unknown constant.In this example,we selectθ(t)=1+0.5 sintandθ(t)=1.4+sint.It is obvious that system(42)satisfies Assumption 1 withp=2,c=max{1,|μ|},τ(t)=0 and Assumption 2 withθl=0.4,θu=2.6.Compared with the examples in literatures [10] and [11],the growth rate of our nonlinear system is no longer a known or an unknown constant,but a time-varying function related to the output.Meanwhile,the range ofθ(t)is not in the vicinity of 1 as in[11],but has been greatly enlarged.

According to Lemma 3,we chooseκ=10.Thus,b2=1.1,ρ1=1.6,ρ2=1.21.Then,letl0=150,l1=151.6 andl2=165.55.Based on Theorem 1,seta1=4,a2=4,σ1=0.45.From(17),we get

Then,π1=0.4,π2=0.8,λmin(PL)=0.3496,λmin(Q)=0.1404,=0.According to (8) and (9),we chooseα=7,β=30.Construct the following controller for the system(42):

The initial conditions are given asx1(0)=1,x2(0)=2,(0)=2,(0)=1,L1(0)=1,L2(0)=1,L3(0)=1 and the parameterμ=3.The simulation results are shown in Fig.1,which verifies that the proposed method is correct and effective.

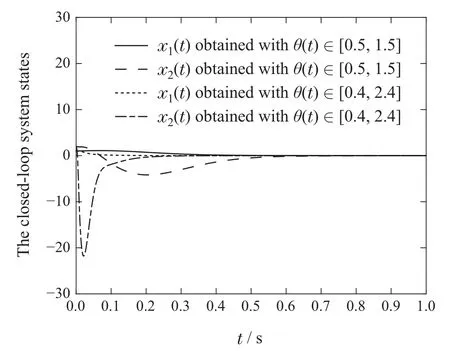
Fig.1 The trajectories of the states of the closed-loop system with different measurement disturbance

Example 2In order to verify that our method is still effective in the presence of time delay,we consider a two-stage chemical reactor system[26]as follows:

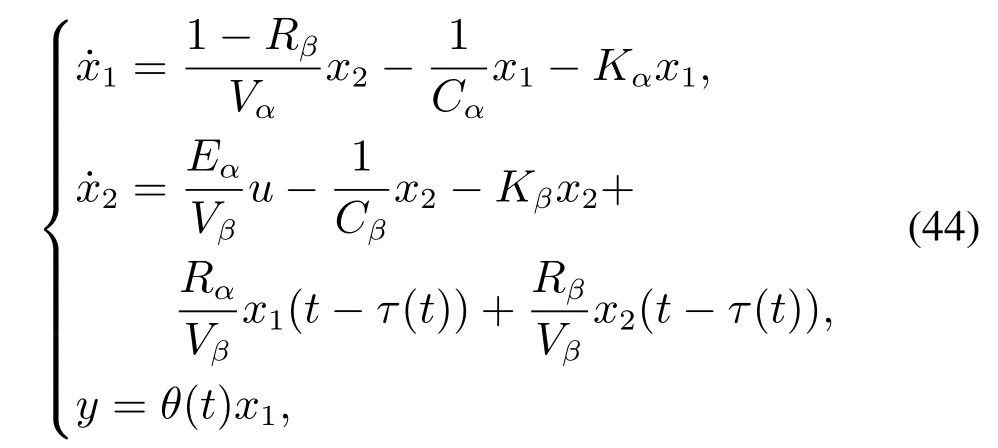
wherex1andx2are the compositions,uandyare the input and output,RαandRβare the recycle flow rates,CαandCβare the reactor residence times,Eαis the feed rate,VαandVβare the reactor volumes,KαandKβare the reaction functions.So as to facilitate the simulation,we choose the following parameters asRα=Rβ=0.5,Kα=Kβ=0.5,Vα=Vβ=0.5,Cα=Cβ=2,Eα=0.5.Then,the system (44) can be transformed into

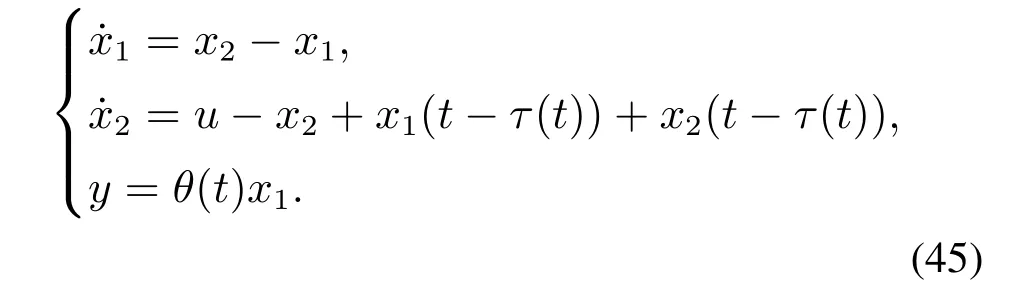
In this example,we choose a non-directedθ(t)=0.4+1.6|cost|.It is easy to verify that system (45)satisfies Assumption 1 withp=2,c=1 and Assumption 2 withθl=0.4,θu=2.According to Lemma 3,we chooseκ=10,thus,b2=1.1,ρ1=1.6,ρ2=1.21.Then,letl0=40,l1=41.6 andl2=44.55.

Based on Theorem 1,seta1=4,a2=4,σ1=0.45,τ(t)=0.8.From(17),we get

The initial conditions are given asx1(0)=1,x2(0)=1,(0)=0,(0)=0,L1(0)=1,L2(0)=1,L3(0)=1 and the parameterμ=3.The simulation results are shown in Fig.2.Obviously,our proposed method is also effective for nonlinear systems with time-delay.

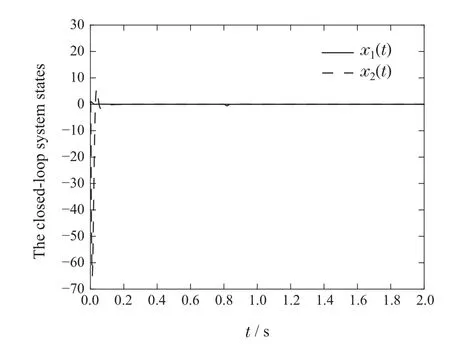
Fig.2 The trajectories of the states of the closed-loop system

Example 3In order to compare the effectiveness of our method with the method proposed in [12],we consider the following nonlinear system[12]:

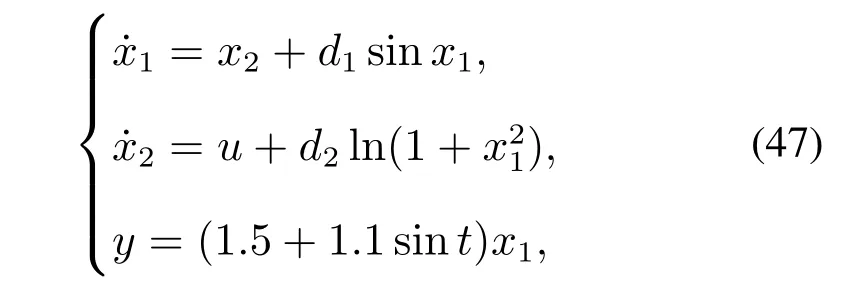
whered1,d2are two unknown bounded time-varying functions andθ(t)=1.5+1.1 sint.As in [12],the following output feedback controller is constructed:

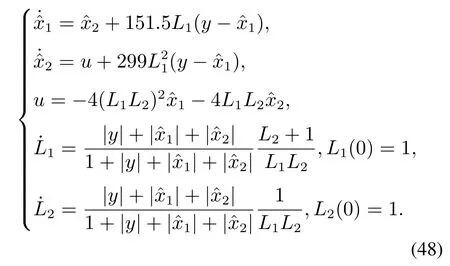
The initial conditions are given asx1(0)=1,x2(0)=2,(0)=2,(0)=1,L1(0)=1,L2(0)=1,L3(0)=1 and the parametersd1=1+cost,d2=2-sin(20t).The simulation results are shown in Fig.3.It can be seen that the system(47)under our presented output feedback controller has a faster convergent speed than that under the controller(48).

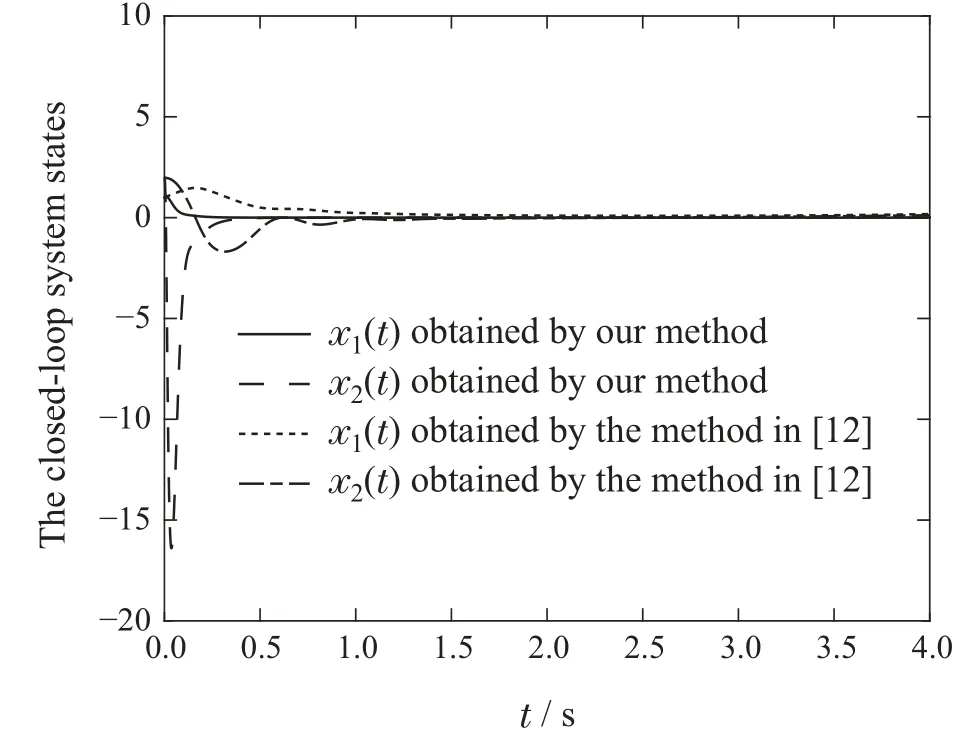
Fig.3 The trajectories of the states of the closed-loop system with different methods

6 Conclusion

In this paper,we studied anti-measurementdisturbance stabilization for a class of nonlinear systems with unknown growth rate,unknown measurement uncertainty,and time-delay.First,a useful matrix inequality was developed.Then,by using three time-varying gains,an output feedback controller was designed to stabilize the nonlinear system.Based on the obtained matrix inequality and a specially constructed Lyapunov-Krasovskii functional,we derived sufficient conditions to ensure the closed-loop system was asymptotically stable.Finally,numerical simulations were applied to verify the correctness of our theoretic results.