切换自治系统的动态输出反馈镇定
2022-11-07孙振东王苗苗
孙振东 ,王苗苗
(1.山东科技大学电气与自动化工程学院,山东青岛 266590;2.中国科学院数学与系统科学研究院系统控制重点实验室,北京 100190)
1 引言
切换系统由若干动态子系统和一个在子系统间进行切换的监控装置组成.这类系统包含连续的系统动态、离散的逻辑动态及其相互作用,是一类基本而典型的混合动态系统.在建模层面上,切换系统能够较精确地描述许多工程系统,例如:具有典型切换特性的电力电子系统[1-2]、逻辑系统[3-4]、机器人系统[5]、病毒传播[6]等.此外,切换系统的研究对于深入理解经典控制理论中一些重要的问题,比如,自适应控制问题、智能控制问题、鲁棒控制问题等,具有重要的价值[7-9].
对切换系统的研究自1960年代起就受到一些学者的关注,并从1990年代起成为国际自动控制界和计算机界一个持续的研究热点和主流方向.针对切换系统的稳定性、能控能观测性、二次最优设计等核心问题,发展了共同Lyapunov方法、多Lyapunov方法、平均方法等理论工具,这些工具不仅推动切换系统研究取得重要进展,而且有关理论和方法还成功应用于多智能体协同控制、信息物理系统等多个新兴领域[10-14].
切换线性系统镇定问题是寻找适当的反馈控制输入/切换策略使得切换(受控)系统指数稳定.作为切换动态系统的核心理论难题,切换镇定问题受到广泛关注[15-20].随着研究的深入,对镇定问题的复杂性有更深入的理解:1)可镇定的切换自治系统不一定具有凸(control-)Lyapunov函数[21],这表明基于凸泛函搜索的算法设计只能提供镇定问题有解的充分条件;2)如果每个子系统只配置一个线性反馈增益,那么能控性不足以保证系统可镇定[11].这些内在特征揭示了切换系统镇定问题具有明确的非凸/非线性/时变特性,表明镇定问题是深具挑战性的问题.
本文针对没有控制输入的离散时间切换线性自治系统,寻求适当的切换规则实现切换系统的指数稳定性.对二阶连续时间切换自治系统,已有可验证的构造性设计[22-23].对一般连续时间/离散时间切换自治系统,文献[24]提出分路径状态反馈的切换策略,证明系统可镇定的充要条件是存在此类切换策略实现系统稳定.本文考虑系统状态不完全可量测的情形,提出基于观测器反馈的切换策略,在系统切换可观测的假设下给出切换线性自治系统的构造性设计.切换系统的观测器构造设计可以视为反馈镇定设计的对偶问题,其挑战性包括:1)对切换系统的反馈镇定问题,目前的主要成果是针对特定系统类,比如,低阶系统,尚缺乏针对一般系统的反馈镇定设计方法;2)对于Luenburger型观测器,观测器本身就是切换系统,且其切换信号不独立(与原系统共享切换信号).当把观测器嵌入切换策略时,必须同时兼顾原系统和观测器系统,即需要设计同时镇定原系统和观测器系统的共同切换策略.本文基于对实现能控/能观测切换信号的新进展[26],提出一类具有时变增益的Luenburger型观测器,可在有限时间实现对系统状态的无差估计,并在此基础上发展分路径观测器反馈的切换策略,实现对原系统和观测器系统的共同镇定.
2 预备知识
2.1 系统描述
记R是实数集,Rp和Rn×m分别是p维实(列)向量和n×m实矩阵.记N+是非负整数集.设s1,s2∈N+且s1<s2,记

2.2 切换路径
切换路径是定义在有限(离散时间)区间上的时间驱动切换信号:给定自然数s2>s1,称θ:1,s2为定义在区间1,s2上的切换路径.

显见,两个切换路径的串接仍为切换路径.多个路径的串接可循结合律定义.
2.3 状态观测器
对切换系统(1),当系统状态不完全可量测时,可通过输出量测获得状态的估计.本文考虑的观测器形式为
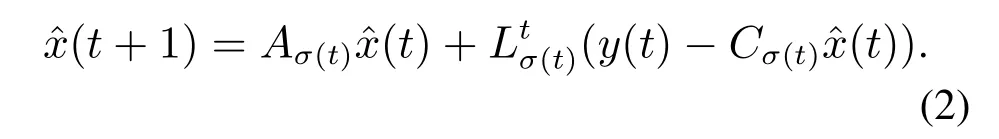
观测器与切换系统共享同一切换信号,因此这里的切换信号不是独立变量.注意到观测器增益矩阵不仅依赖切换信号,而且是显示依赖时间的,这表明要为同一个子系统配置多个线性增益矩阵.考虑到系统初始状态未知,本文设置观测器初态为原点,即=0.把观测器(2)从初始沿切换信号σ的轨线记为
给定切换信号σ,称观测器(2)对系统(1)的观测是σ-渐近的,如果有

定义1[11]称切换系统(1)是可观测的,如果存在t1>t0,使得初态x(t0)可由输出y(t),t ∈[t0,t1)唯一决定.
2.4 反馈镇定问题
定义2[24]称切换系统(1)是可(状态反馈指数)镇定的,如果存在正实数α <1,β≥1使得对所有初态x0∈Rn都存在切换信号σ(t)满足
1.3 聋生掌握计算机水平的参差不齐,聋生能力的差距导致聋生完成任务所需时间存在较大差异。大大影响着教师的授课及课堂目标的完成。

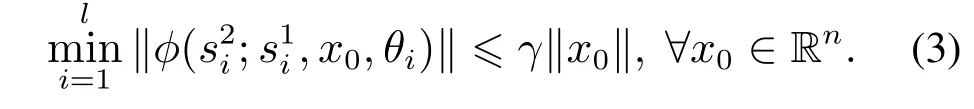
定义3称切换系统(1)是可动态输出反馈镇定的,如果存在正实数α <1,β≥1及状态观测器(2)使得对所有初态x0∈Rn都存在观测器驱动切换信号σ(t)满足
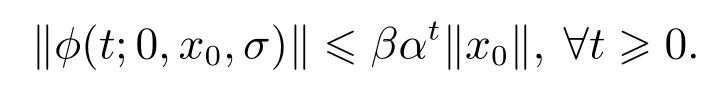
本文探讨的反馈镇定问题是寻求适当的基于观测器的切换策略使得增广系统(1)-(2)是指数稳定的.
3 主要结果
假设1切换系统(1)是可镇定的.
假设2切换系统(1)是可观测的.
由切换系统可观测性质[11],存在j1∈M,p维行向量Hj1,及矩阵集Gi ∈Rn×p,i ∈M使得切换系统


注1由估计误差动态(8)可知,当估计误差在某一时刻为零,则误差在其后的所有时刻都为零.这表明观测器(2)是θ0-有限时间观测器.
定理2在假设1-2下,切换系统(1)是可动态输出反馈镇定的.
证记Φ为切换系统(1)沿切换律(6)的状态转移矩阵,即

其中ϵ是任意给定的正实数.
定义切换路径

注2定理2给出的观测器和切换策略设计是交互式递推定义.首先,解决基于分路径状态反馈的镇定问题,获得一组满足状态模压缩的切换路径;再寻求实现可观测性的切换路径.将这两组路径进行适当组合,获得一组既满足模压缩又实现可观测性的(共同)路径集.实现动态观测器反馈的切换策略是对共同路径集通过特定时刻(t0,t1,···)观测器状态进行反馈,从公共路径集中选择对观测器状态模压缩的路径,由此迭代获得定义在时间空间(N+)上的切换策略.观测器增益矩阵是准周期选定的:在+1的子区间依次选定n个时刻施予不同增益,其余时间的增益均为零.
4 示例
考虑包含两个子系统的二阶切换系统(1),其中:
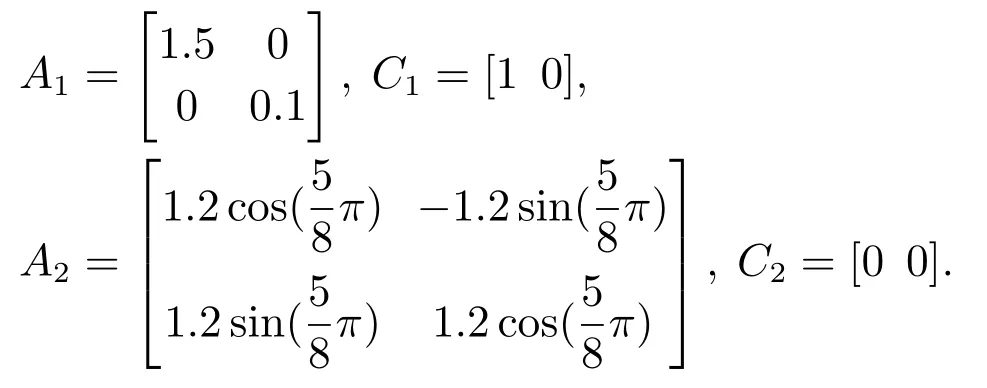
容易验证此系统可观测,可镇定,但不存在凸(control-)Lyapunov函数[21].
经计算可知

另一方面,可以求得具有状态模压缩性质的切换路径
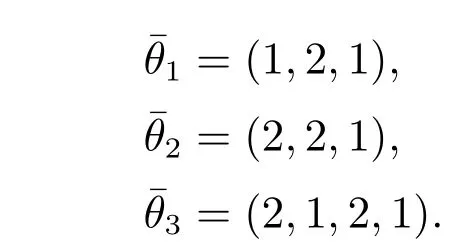
基于上述推导,可以通过式(10)迭代给出观测器和切换策略设计.
给定初态x0=.图1给出了系统轨线、观测器轨线及对应的切换信号.可以看出,系统轨线指数收敛,观测器轨线和系统轨线在第4 s及以后重合.
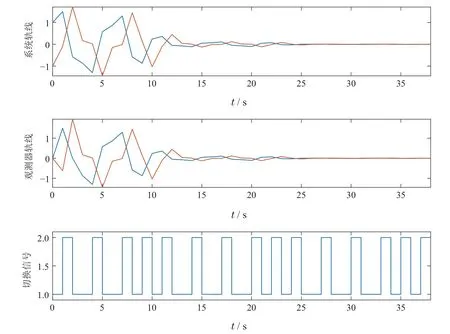
图1 系统轨线、观测器轨线及切换信号Fig.1 State,observer,and switching signal
为展示本文设计方案的鲁棒性能,假设系统受到(时变/状态依赖)混合干扰
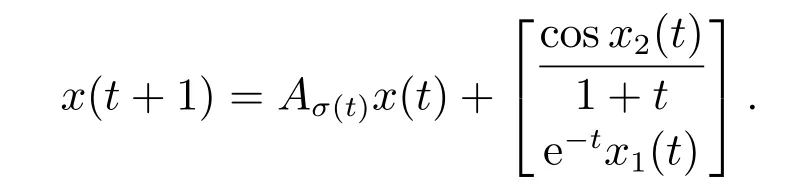
图2给出了对应的系统轨线、观测器轨线及对应的切换信号.尽管系统出现更大的超调,系统轨线仍指数收敛.
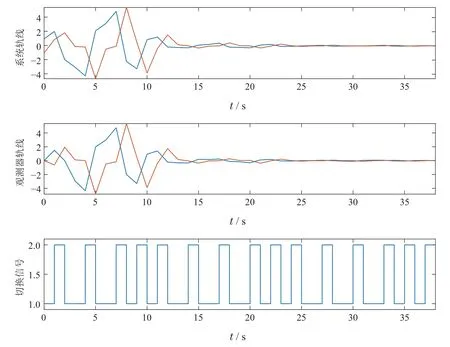
图2 受扰的系统动态Fig.2 Disturbed dynamics
5 结语
针对离散时间切换线性自治系统,在系统可观测的假设下,设计了一类具有时变增益的切换观测器,证明观测器可在有限时间内获得系统状态的精确估计.进一步,在系统可镇定的假设下,设计了基于分路径观测器驱动的切换策略,证明系统轨线指数收敛.所给出的观测器设计和切换信号设计是构造性的.仿真示例表明本文提出的设计方案是可行性,同时具有一定的鲁棒性.
