CLF-CBF-QP新形式下非线性系统的安全攸关控制与优化
2022-11-07龙离军胡腾飞
龙离军,胡腾飞
(东北大学信息科学与工程学院,辽宁沈阳 110819)
1 引言
随着移动机器人的应用越来越广泛,许多新的或具有挑战性的课题被提出,例如,如何实现机器人的安全攸关控制,从而避免其与人或物相碰撞[1-4].因此,为了确保机器人能正常运行,制定实时避障策略来保证动态系统的安全性是必要的.目前,已有许多算法专注于机器人的避障问题,如:全局路径规划算法[1-2]提供了从起点到终点的一条最优路径,然而这种算法只能应用于全局信息已知的情形.基于人工势场(artificial potential field,APF)和栅格法的虚拟力场法(virtual force field,VFF)[5]可以实现机器人实时避障,但这种方法信息存储量大且获得的控制器不是最优的.Hamilton Jacobi可达性分析法(Hamilton Jacobi reachability analysis,HJ-RA)[6]是一种验证动态系统安全性的形式化方法,该方法在避免不安全集受有界不确定性影响的前提下,将动力系统驱动到目标集,然而,可达性分析随系统维数的增加(呈指数增长)而变得难以计算.
近年来,一种基于集合前向不变性以实现系统安全攸关控制的控制障碍函数(control barrier function,CBF)[7]被提出,且APF为其特例[8].由于CBF具有可扩展性、强实时性和鲁棒性[9]等优点,其常与PID,控制Lyapunov 函 数(control Lyapunov function,CLF)以及反步法等算法相结合并利用二次规划(quadratic programming,QP)实现系统的最优安全轨迹跟踪控制[10-12].该算法的有效性和优越性在许多领域得到验证并广泛应用,例如:双足机器人[13]、自动驾驶汽车[14]、四旋翼无人机[15]、多智能体系统[16]等.此后,CBF得到诸多学者研究和扩展,例如:文献[17]和[18]分别提出指数和高阶CBF用于处理高相对阶系统的安全控制问题,文献[19]根据系统状态和输入定义的积分CBF可应用于非仿射控制系统,文献[20]和[21]分别提出鲁棒自适应和自适应滑模CBF用于处理具有未知参数不确定系统的安全控制问题.此外,CBF从连续时间控制系统推广到了离散时间控制系统中[22-24].最近,CBF被应用于基于机器学习数据驱动作用下的安全控制[25-26].文献[27]对CBF的发展进行了综述.
然而,在实际工程应用中,由于物理限制,智能体系统通常需要考虑容许控制输入等附加约束,但该约束可能与CLF和CBF约束发生冲突,从而导致QP变得求解不可行.另外,值得注意的是,当需要考虑系统自身体积或运行环境中存在快速移动障碍物等问题时,需时刻保证系统与障碍物之间有一定安全距离以降低发生碰撞的风险.在前人的一些研究工作中[28-30],使用CLF-CBF-QP实现安全控制时并没有考虑控制输入约束,这意味着可能由于物理限制而导致系统无法正常执行操作.虽然文献[31-32]在QP中显式考虑了控制输入约束,但仍没有处理输入约束与CLF和CBF约束之间存在的潜在冲突.文献[33]虽然提出一种CBF的最优衰减形式来提高优化问题的可行性,且CBF的衰减率在时间上是逐点优化的,却没有考虑系统自身体积和环境中存在动态障碍物等问题,当该方法被应用于上述情况时,系统的安全性难以保证.
因此,针对上述关于QP求解可行性和动态系统的安全性问题,本文的主要工作和创新点如下: 1) 分别从控制输入空间和状态空间的角度分析CLF和CBF中参数γ和λ对QP求解可行性和系统性能的影响;2) 提出CLF-CBF-QP新形式,以此提高优化问题的可解性;3) 设计CBF新形式,以此提高动态系统在考虑自身体积或在具有动态障碍物环境中运行时的安全性;4) 通过线性平面四旋翼安全轨迹跟踪验证所提出方法的可行性和有效性.
2 基础知识
2.1 符号定义
x:=(p,,q)∈Rn表示动态系统的状态,其中p∈Rk为系统在k维空间中的位置状态,q∈Rn-2k为除了位置状态p和速度状态的其他状态.0n×m表示n×m维零矩阵,In表示n维单位矩阵.∂S表示集合S的边界.对于a,b >0,如果连续函数α:(-b,a)→(-∞,+∞)严格单调递增且α(0)=0,那么称α为扩展的K类函数.如无特殊说明,QP指CLF-CBF-QP.
2.2 控制Lyapunov函数
考虑如下仿射非线性系统:
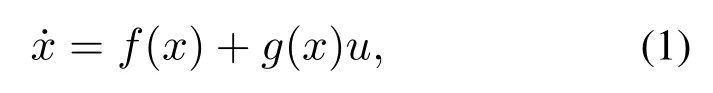
其中:x ∈D ⊂Rn,u ∈Uadm⊂Rm分别是系统状态和控制输入,Uadm是容许控制输入集,f(x)和g(x)是局部Lipschitz函数.
定义1[11]对于仿射非线性系统(1),如果存在正常数c1,c2和γ,使得对于所有x ∈D,连续可微函数V:Rn →R满足
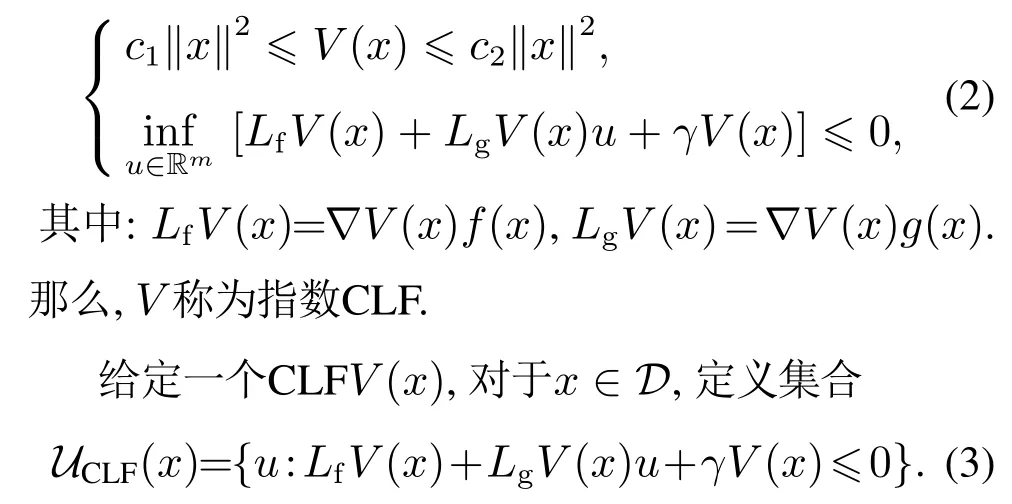
定理1[27]对于仿射非线性系统(1),如果存在满足式(2)的CLFV,那么任意Lipschitz连续反馈控制器u(x)∈UCLF使系统渐近稳定到平衡点x*=0.
由于约束(2)关于u是仿射的,因此,利用QP可获得最优镇定控制器,其形式为
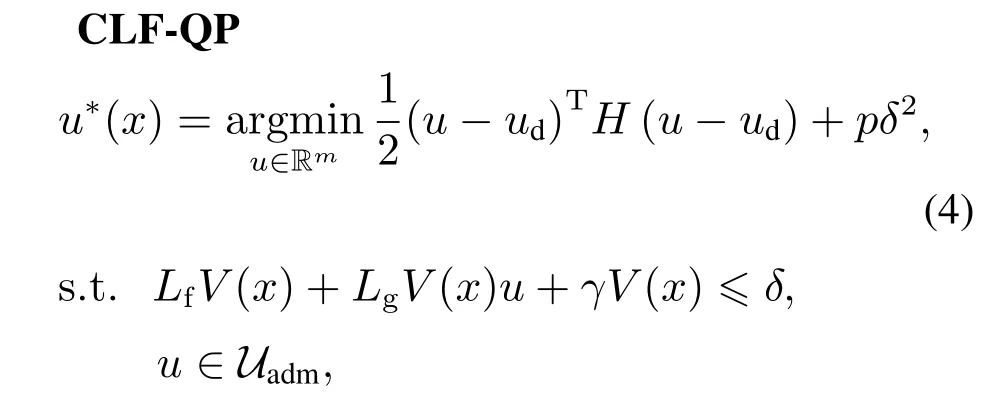
其中:H为正定矩阵,ud为期望输入,p >0为惩罚因子,δ为松弛变量.当CLF和控制输入约束冲突时,通过δ放宽系统稳定性而提高QP求解可行性.
2.3 控制障碍函数
定义2[11]给定一个连续可微函数h:D →R,定义零超水平集

其中:H为正定矩阵,ud为期望输入.
2.4 利用QP结合CLF和CBF
Ames[7]等人首次利用QP将CLF和CBF约束相结合构造最优安全镇定控制器以实现自适应巡航控制,其具体形式为

其中:H为正定矩阵,常数γ,λ≥0,p >0为惩罚因子,δ为松弛变量.当CLF,CBF和控制输入约束冲突时,通过δ放宽系统稳定性而提高QP可行性.该形式的QP被广泛地应用于各种安全攸关控制中[31-33].
2.5 平面四旋翼线性模型
假设1四旋翼布局对称且质量分布均匀.
考虑如图1所示平面四旋翼控制系统.图1的动力学模型为

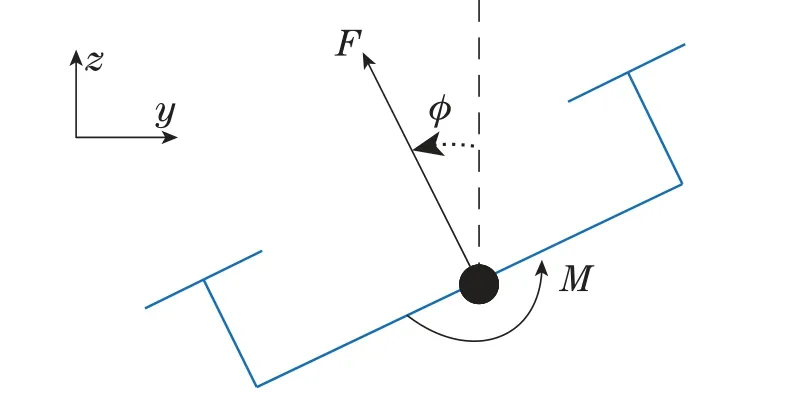
图1 平面四旋翼模型Fig.1 Model of planar quadrotor
为获得平面四旋翼线性模型,考虑在平衡点(悬停状态)xe=06×1,ug=[mg 0]T处利用泰勒展开进行线性化处理

2.6 不规则障碍物圆形近似化
在实际环境中存在的障碍物多为不规则形状,但CBF的设计涉及系统与障碍物距离的计算,为方便理论计算与仿真验证,对不规则静或动态障碍物通过以下两种方式近似化处理[35],其如图2所示

图2 不规则障碍物近似化处理Fig.2 Approximation processing of irregular obstacles
·不规则球形状障碍物近似为单个半径为r的圆形或球形.
·不规则长条状障碍物近似为多个半径为r的圆形或球形组合而成.
2.7 控制问题描述
定义4标量函数d(p,o)被定义为
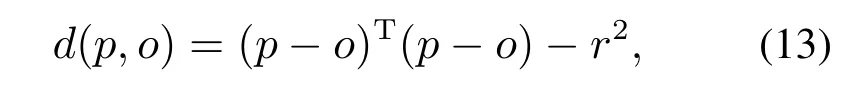
其中:p ∈Rk为动态系统的位置状态,o ∈Rk,r分别表示在k维空间中障碍物的中心位置和半径.
于是,系统相对于第i ∈{1,2···,n}个障碍物的几何安全区域被定义为Si={p ∈Rk|d(p,oi)≥0}.因此,系统的整体安全区域为S=
假设2为保证系统正常运行,对于∀t >0,安全区域S非空.

3 主要结论
动态系统能否正常运行与QP求解可行性息息相关.当QP选择为式(9)时,由于考虑控制输入约束u∈Uadm,可能导致QP求解不可行.另外,CBF的设计需要考虑这一问题:当系统体积不能被忽略或环境中存在快速移动的障碍物时,动态系统极有可能与障碍物相碰.因此,为了降低系统碰撞障碍物的风险,本文设计一种CBF新形式以提高系统的安全性.
3.1 输入空间角度分析QP求解可行性

基于假设3,为了直观起见,本文从几何的角度进行QP可行性分析.图3中凸多边形区域表示允许控制输入集,绿色区域表示Ufea(xt),箭头方向表示集合的半空间方向.
1) 如图3(a)所示情况,此时Ufea(xt)=Uadm,QP求解可行.CLF和CBF约束在优化问题中不起作用,且最优值在∂Uadm处获得.
2) 如图3(b)所示情况,此时Ufea(xt)/=∅,QP求解可行.当CLF约束起作用时,QP最优值在∂UCLF(xt)处取得,当CBF约束起作用时,QP最优值在∂Uabf(xt)处取得,若在Uadm的顶点处取得最优值时,那么,CLF和CBF约束将都不起作用.
3) 如图3(c)所示情况,此时QP求解可行,且CLF和CBF约束都起作用,QP的最优值在∂UCLF(xt)和∂UCBF(xt)处取得.
4) 如图3(d)所示情况,此时Ufea(xt)=∅,QP求解不可行.
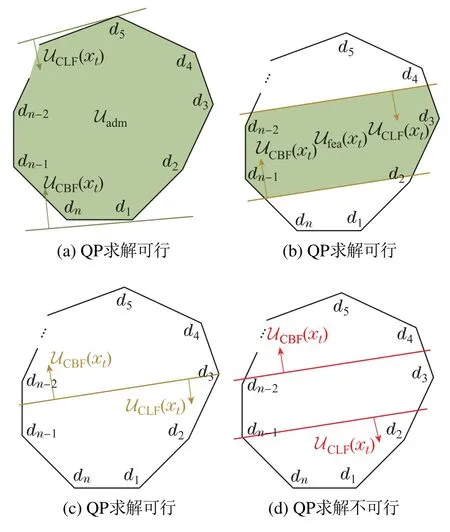
图3 QP求解可行性分析Fig.3 Feasibility analysis of QP
根据上述分析可知,QP求解可行性与CLF和CBF约束相关,即与正常数γ和λ有关.因此,接下来分析γ和λ的数值大小对QP求解可行性和系统性能的影响.受文献[33]的研究思路启发,本文将从状态空间的角度分析γ和λ对QP求解可行性的影响.
3.2 γ和λ对系统性能和QP求解可行性的影响
3.2.1 γ对系统收敛速度的影响

根据式(2)和式(16),利用比较引理[34]易知
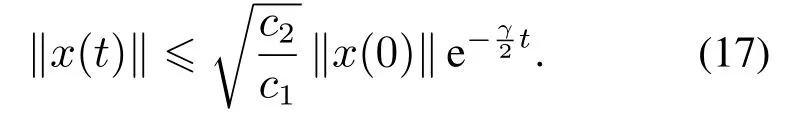
由式(17)知,‖x(t)‖以不小于的速率收敛到0.因此,增大γ将加快系统收敛速度,但会降低QP求解的可行性,这将在下一节中进行讨论.
3.2.2 γ对QP求解可行性的影响
定义6状态集合R=R(xt,Uadm,Δt)表示在满足系统(1)和控制输入约束Uadm时,系统在状态xt处经过极小时间Δt后所能达到的状态集.

3.2.3 λ对系统安全性能的影响
根据CBF约束式(6),利用比较引理可得
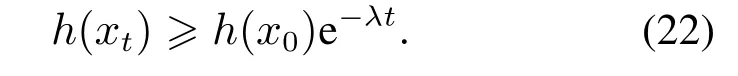
为了确保h(x)有下界,λ≥0.
根据式(22)可知,当t确定时,随着λ的逐渐减小,h(x0)e-λt逐渐增大,即系统距离∂C越远.考虑λ=0时(x)≥0这一极端情况,系统将随时间t逐渐远离∂C.所以,减小λ将使系统的安全性更容易得到保证.然而,由式(6)可知,减小λ将导致CBF约束的加强,从而,QP求解可行性也随之降低,在下一节中将通过几何关系进行更直观的分析.
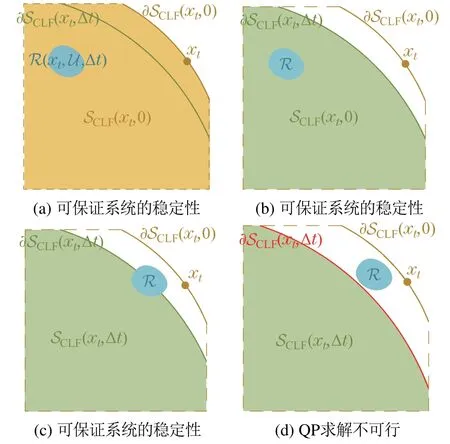
图4 系统稳定性和QP可行性的分析Fig.4 Analysis of system stability and QP feasibility
3.2.4 λ对QP求解可行性的影响
在时间区间[t,t+Δt]内,根据式(6),可得

因此,在状态空间中,定义在x(t+Δt)时满足CBF约束的超水平集为
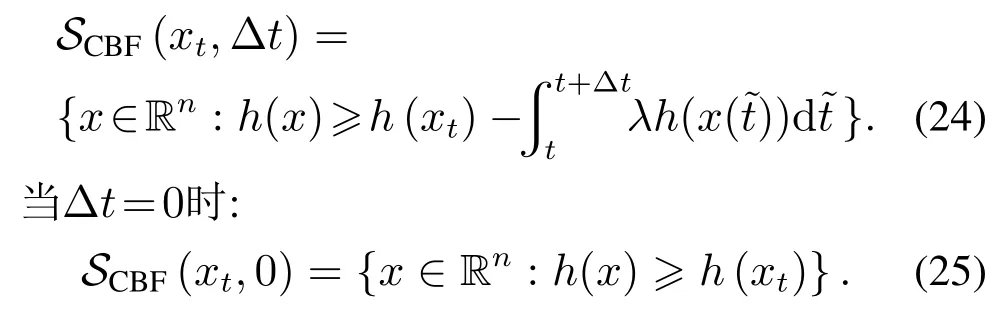
注2SCBF(xt,0)⊂SCBF(xt,Δt)总是成立的.
因此,若R(xt,Uadm,Δt)∩SCBF(xt,Δt)=∅,则表明QP在状态xt处求解不可行.接下来,本文将通过绘制几何关系来直观的描述λ对QP求解可行性的影响.
如图5所示,定义障碍物外部区域为安全空间,红色区域表示不安全区域(障碍物),蓝色区域表示R(xt,Uadm,Δt),黄色区域表示SCBF(xt,0),黄色实线表示∂SCBF(xt,0),绿色区域表示SCBF(xt,Δt),绿色实线表示∂SCBF(xt,Δt).根据不同情况对QP求解可行性进行分析.
1) 如图5(a)所示情况,R∩SCBF(xt,Δt)/∅且R∩SCBF(xt,0)=R,所以系统将朝远离障碍物的方向移动,系统的安全性可以被保证.又由于R⊂SCBF(xt,Δt),所以此时CBF 约束在优化问题中不起作用,QP求解可行性与CLF约束相关.
2) 如图5(b)所示情况,R∩SCBF(xt,Δt)/∅且R∩SCBF(xt,0)⊂R,所以系统可能朝靠近或远离障碍物的方向移动,但系统的安全性仍可以被保证.此时CBF约束在优化问题中不起作用,QP求解可行性与CLF约束相关.
3) 如图5(c)所示情况,R∩SCBF(xt,Δt)∅且R∩SCBF(xt,0)=∅,所以系统将朝靠近障碍物的方向移动,但系统的安全性仍可以被保证.此时CBF约束是否起作用取决于λ的取值,且QP求解可行性与CLF约束相关.
4) 如图5(c)-(d)所示情况,当Δt一定时,随着λ数值的逐渐减小,根据式(24)可知,SCBF(xt,Δt)的区域也将逐渐缩小,进而导致R ∩SCLF(xt,Δt)=∅,此时QP求解不可行,系统的安全性无法被保证.
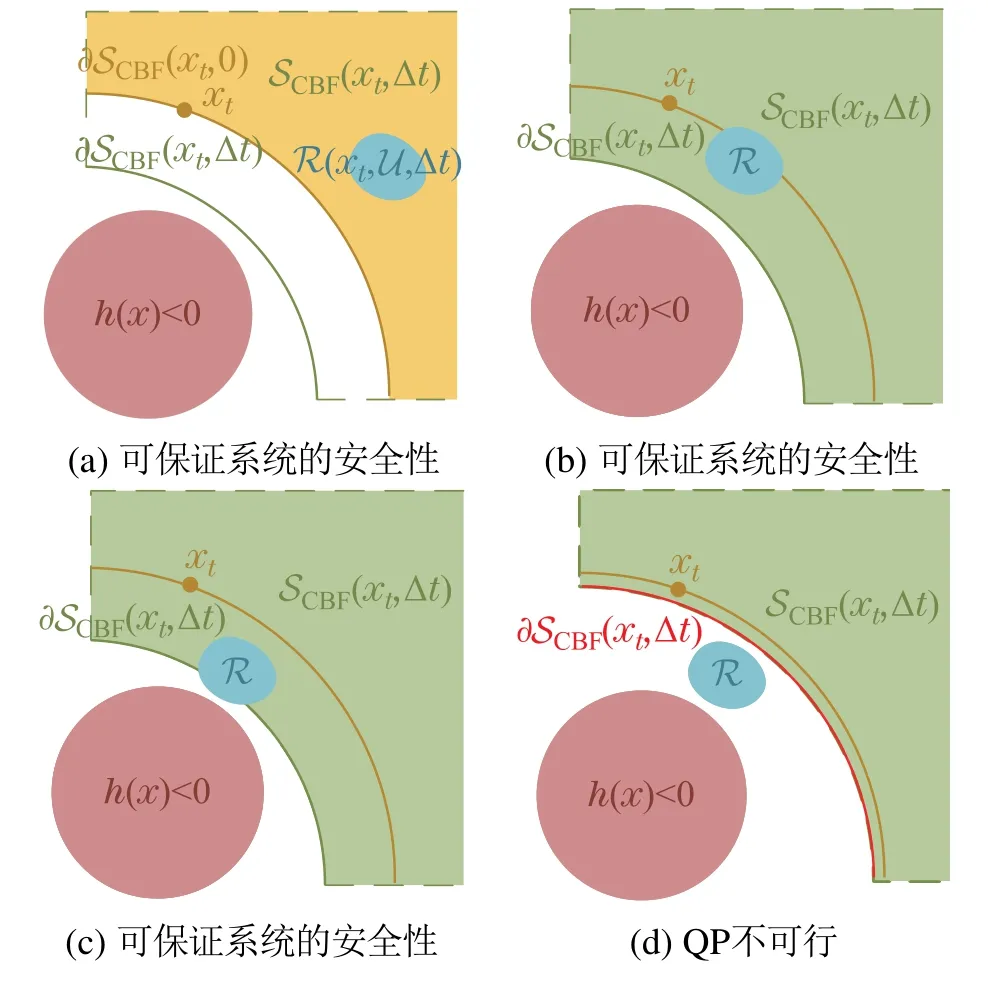
图5 系统安全性和QP可行性的分析Fig.5 Analysis of system safety and QP feasibility
根据上述分析,γ和λ对系统性能和QP求解可行性影响的结论如表1所示.

表1 γ和λ对性能的影响Table 1 Performance effects of γ and λ
当同时考虑CLF,CBF和控制输入约束时,若R(xt,Uadm,Δt)∩SCLF(xt,Δt)∩SCBF(xt,Δt)/∅,则QP求解可行,系统可实现最优安全镇定控制.
3.3 设计QP新形式

其中:H为正定矩阵,常数q,p >0为惩罚因子,正常数ud,γd,λd为期望值,γ和λ为决策变量.
根据式(26),λ非负,因此,需要始终确保系统的安全性.当系统靠近障碍物时,决策变量γ减小,λ增大,在确保系统安全的前提下放宽稳定性约束以此提高QP求解可行性.当系统远离障碍物时,由于成本函数中的惩罚项,使得γ最终会达到期望值γd,因此系统的稳定性得到保证.
注3虽然提出的QP(26)新形式可以提高优化问题求解可行性,但当输入约束较苛刻时,QP仍变得求解不可行.
3.4 设计CBF新形式
本文基于文献[10]中CBF的形式定义标量函数
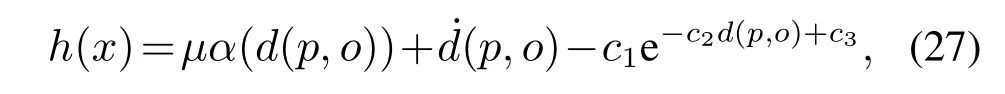
其中:μ,c1,c2,c3>0为常数,α为扩展的K类函数,标量函数d(p,o)为式(13).
假设4对于仿射非线性系统(1),系统速度状态∈Rk的微分为
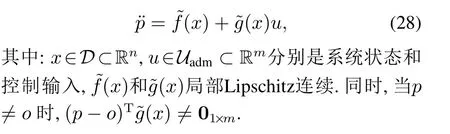
定理3对于满足假设4的仿射非线性系统(1),式(27)为全局有效CBF,且保证系统与障碍物间始终保持安全距离.
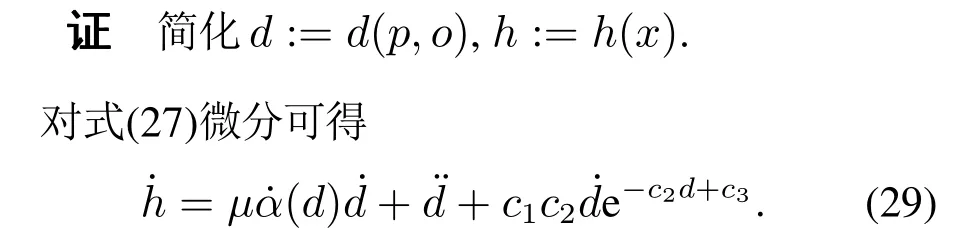
根据式(13),可得

注4通过调节正常数c1,c2,c3可以改变系统与障碍物间的最小距离,但c1的选取不能太小.
4 仿真验证
在假设1-4满足的前提下,本文使用线性平面四旋翼(12)在具有障碍物的环境中进行轨迹跟踪控制1仿真案例视频链接: https://b23.tv/vZL2yN2..同时,基于MATLAB(R2019b)仿真平台,“ode45”微分方程求解器,YALMIP最优化工具箱和IPOPT“内点法”求解器来验证所提出算法的有效性和优越性.仿真中所用参数如表2所示.
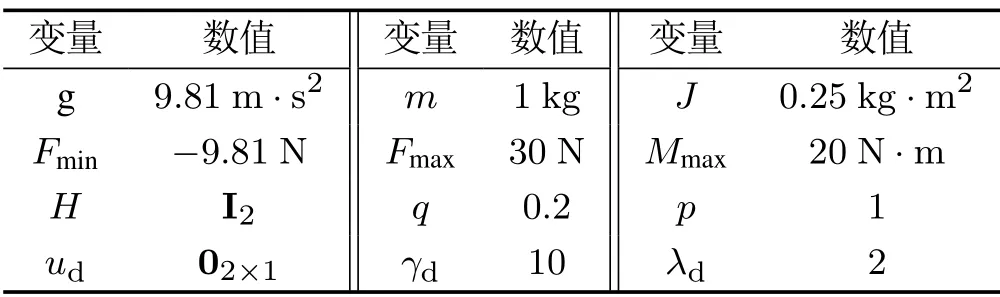
表2 仿真中使用的参数值Table 2 Parameter values used in simulation
注5由于平面四旋翼动力学模型在线性化过程中进行变量替换=u-ue,ue=[mg 0]T.因此,设置Fmin=-9.81 N.另外,对于平面四旋翼线性模型(12),仅当四旋翼与障碍物中心位置在同一水平线上时,(p-o)T(x)/01×m,此时,假设4不成立,本文中该情况被忽略.最后,为了提高系统的收敛速度和安全性,γd的选取应偏大,λd的选取应偏小.
为了确保系统的稳定性,本文根据文献[24],选择CLF为
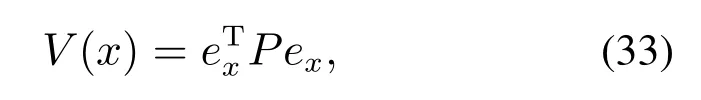
其中:ex=x-xd,x为系统状态,xd为期望状态,P为正定矩阵,仿真中通过MATLAB内置函数lqr获得P.
4.1 动态障碍物环境中避障失败
给定参考轨迹为
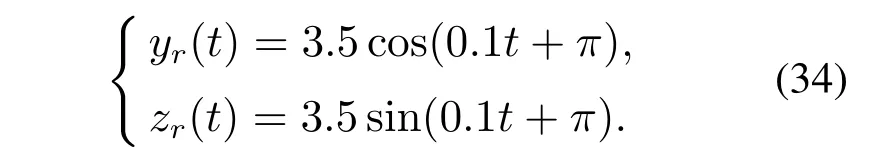
半径为1的动态障碍物1的移动轨迹为
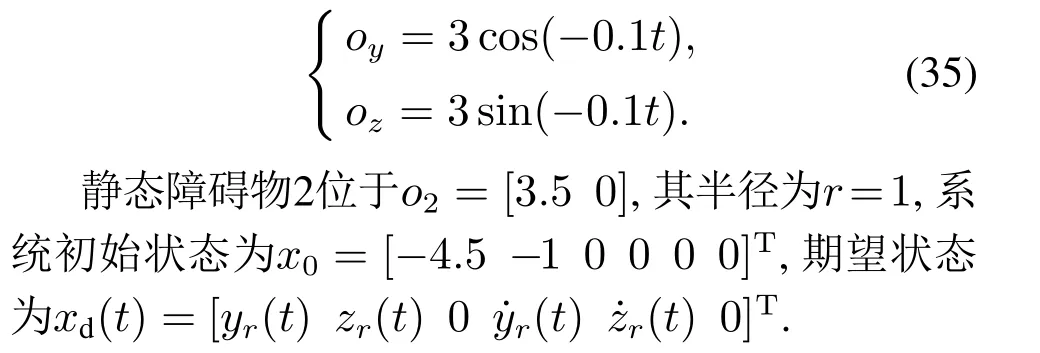
根据文献[10],选取CBF的形式为
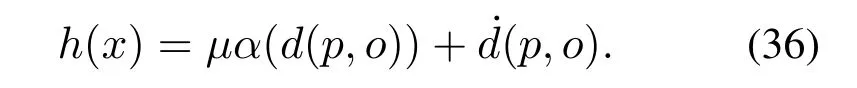
仿真结果如图6-7所示.根据图7可知,当t=15 s时,d(p,o1)<0表示四旋翼与障碍物相碰;当t=35 s时,d(p,o2)=0表示四旋翼紧靠障碍物边缘移动,因此当系统的体积不能被忽略时,四旋翼将与障碍物发生碰撞.由此可知,文献[10]中所设计的CBF不能处理考虑动态系统体积或环境中存在快速移动障碍物时的情况.接下来,将验证本文所给方法的有效性.

图6 平面四旋翼运行轨迹Fig.6 The trajectory of planar quadrotor
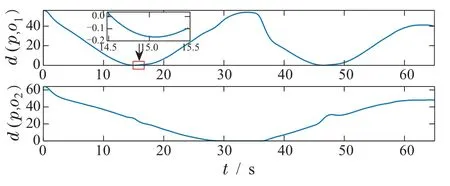
图7 函数d(p,o1)和d(p,o2)Fig.7 Functions d(p,o1)and d(p,o2)
4.2 静态障碍物环境下轨迹跟踪控制
给定系统的参考轨迹为式(34),静态障碍物1,2分别位于o1=[0 3.5]和o2=[0-3.5],其半径为r=1.系统初始状态为x0=[-4.5-1 0 0 0 0]T,期望状态为xd(t)=[yr(t)zr(t) 0(t)(t) 0]T.选择CBF为式(27).
仿真结果如图8-11所示.根据图9可知,d(p,o1)>0,d(p,o2)>0,四旋翼始终与静态障碍物保持一定距离,因此系统触碰障碍物的风险被大大降低.另外,从图10可以看出,当四旋翼靠近障碍物时,γ将减小,λ将增大,从而提高QP可行性使系统能正常运行.根据图11可知,控制输入约束始终得到满足.因此,相比于文献[10],本文所给CBF形式使系统的安全性更高.
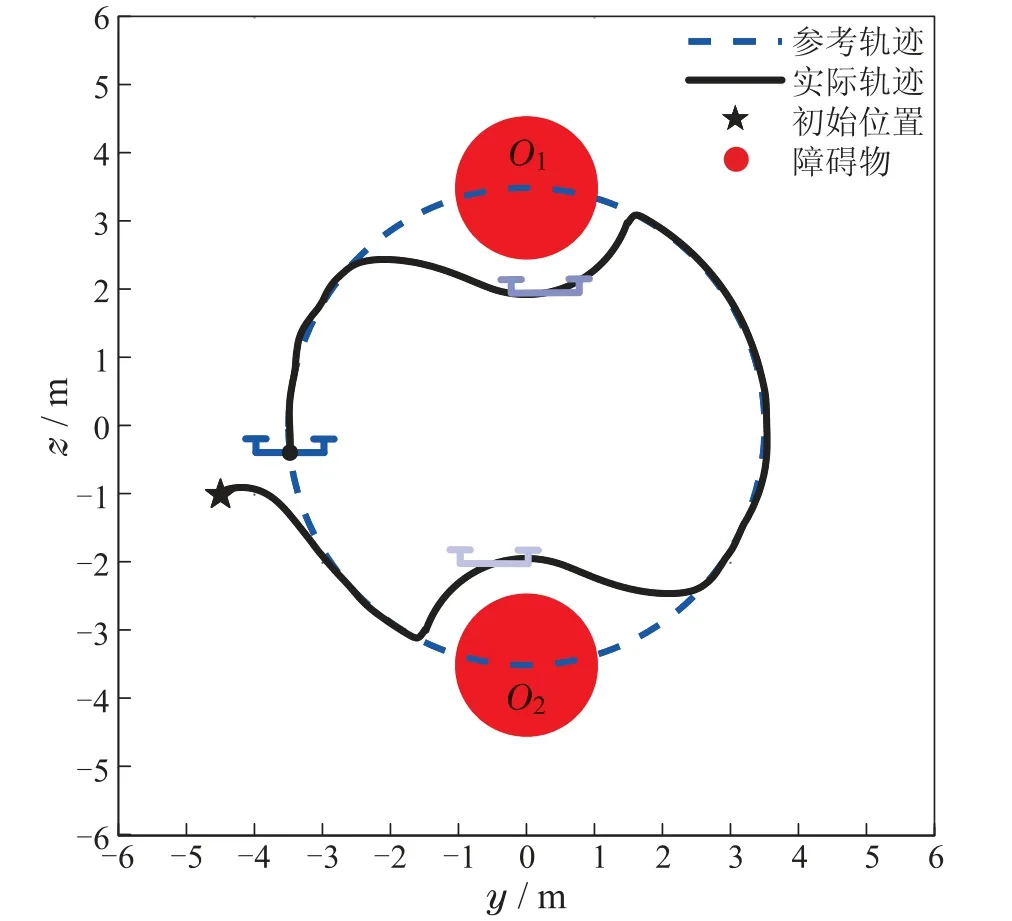
图8 平面四旋翼运行轨迹Fig.8 The trajectory of planar quadrotor
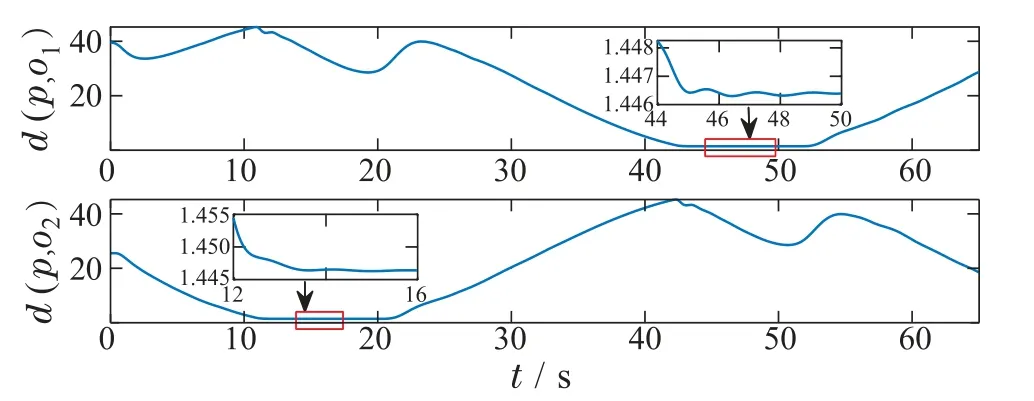
图9 函数d(p,o1)和d(p,o2)Fig.9 Functions d(p,o1)and d(p,o2)
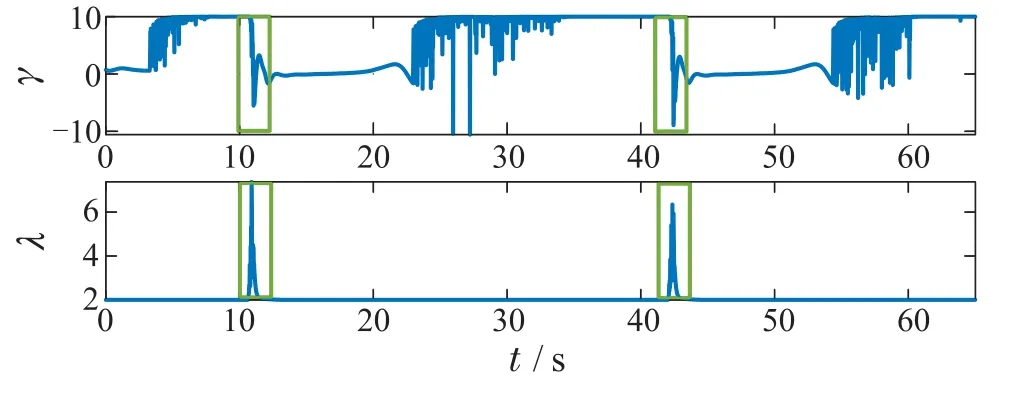
图10 决策变量γ和λFig.10 Decision variables γ and λ
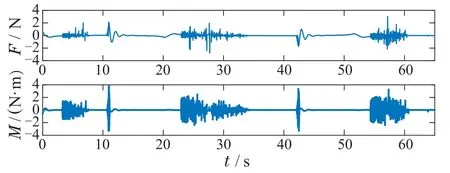
图11 控制输入F和MFig.11 Control inputs F and M
4.3 动态障碍物环境下轨迹跟踪控制
给定系统的参考轨迹为式(34),动态障碍物移动轨迹为式(35).系统初始状态为x0=[-4.5-1 0 0 0 0]T,期望状态为xd(t)=[yr(t)zr(t)0(t)(t)0]T.选择CBF为(27).
仿真结果如图12-15所示.从图13可知,d(p,o)>0,四旋翼始终与动态障碍物保持一定距离,使得四旋翼能及时避开障碍物,系统的安全性得到提高.从图14中绿框区域可以看出,当四旋翼靠近障碍物时,γ将减小,λ将增大,从而提高QP求解可行性使四旋翼能正常运行,从红框区域可以看出,在确保QP求解可行的前提下,λ将减小使得四旋翼能更早避开动态障碍物.另外,根据图15可知,控制输入约束始终得到满足.
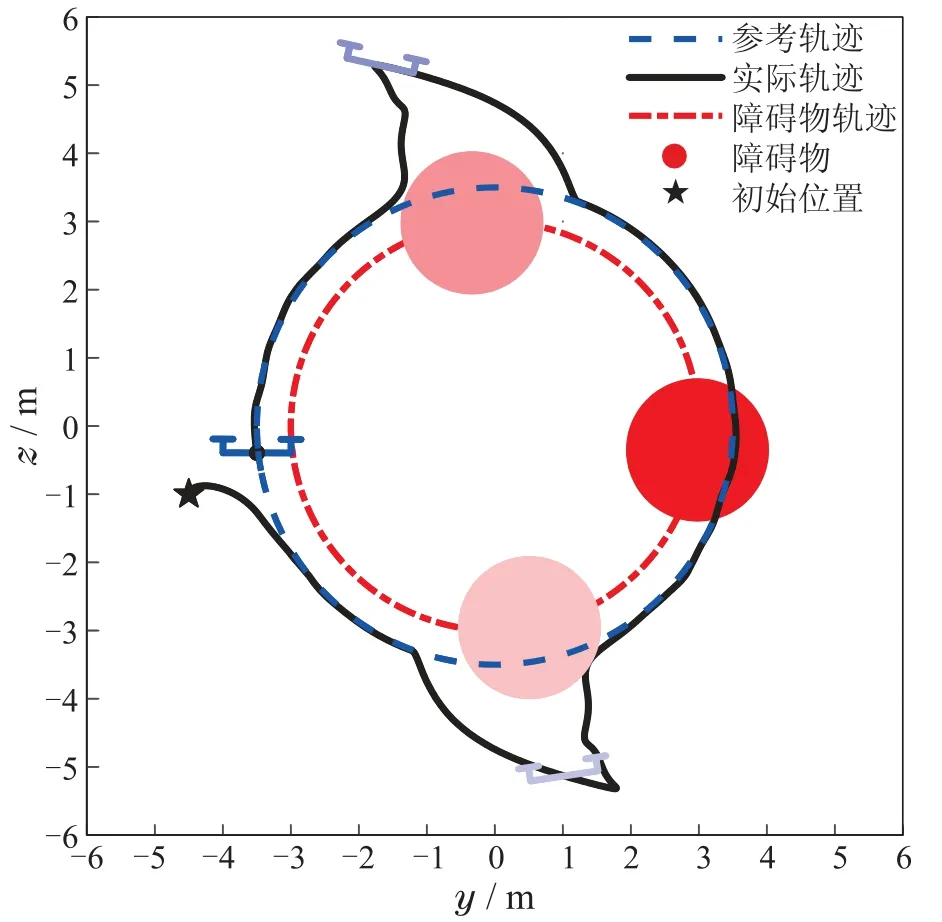
图12 平面四旋翼运行轨迹Fig.12 The trajectory of planar quadrotor
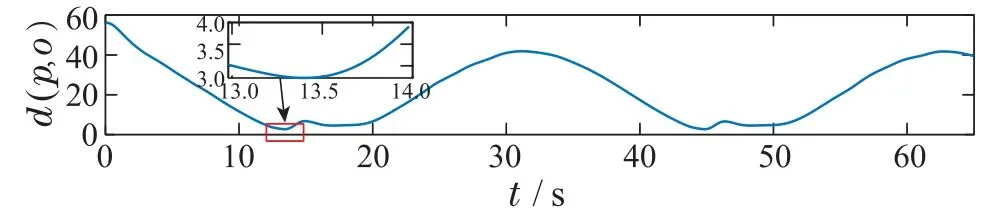
图13 函数d(p,o)Fig.13 Function d(p,o)
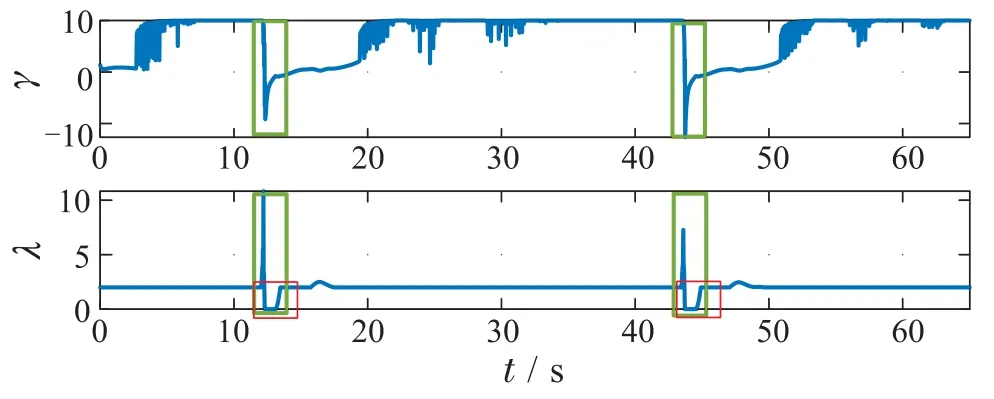
图14 决策变量γ和λFig.14 Decision variables γ and λ
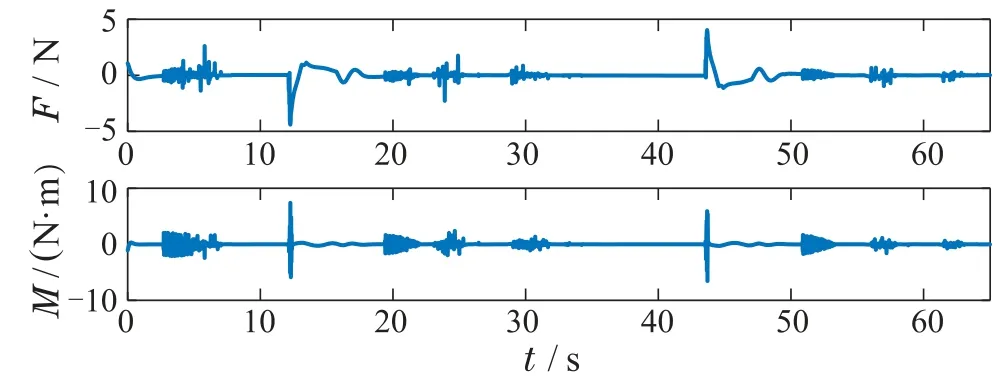
图15 控制输入F和MFig.15 Control inputs F and M
若使用QP(9)并选取常数γ=γd=10,λ=λd=2,当四旋翼靠近动态障碍物时,QP变得求解不可行,其在MATLAB中显示信息为

因此,本文所给QP新形式的可求解性更高.
5 结论
本文从控制输入和状态空间的角度分别分析了QP求解可行性以及γ和λ对QP求解可行性和系统性能的影响,从而提出了一种CLF-CBF-QP新形式,以此来提高优化问题的可行性.另外,本文设计一种CBF新形式,使得当考虑动态系统本身的体积且环境中存在动态障碍物时,仍能保证系统的安全性.最后,通过线性平面四旋翼在具有障碍物的环境中进行轨迹跟踪验证所提出方法的有效性和优越性.值得注意的是,当控制输入约束较为苛刻时,QP仍会变得不可行.如何进一步提高优化问题的可行性,这将是笔者未来研究的重点.
