人造目标散射结构的零极化辨识与应用

吴国庆 陈思伟 李永祯 王雪松

（国防科技大学电子科学学院 CEMEE 国家重点实验室,长沙 410073）

引言

极化是电磁波除幅度、频率、相位之外的另一重要属性[1].具备极化测量能力的雷达系统已经成为当前雷达探测领域的主流传感器，得到越来越广泛的应用[2-6].极化信息的获取使得对目标极化散射机理进行完整刻画成为可能，对于目标散射特性的解译具有重要意义[7-10].

零极化本质上是目标最优极化的一种.目标最优极化是指对于已知散射特性的目标，能够使其接收天线的接收功率达到最大值或者最小值的发射和接收天线极化状态.目标最优极化的概念由Kennaugh于1952 年首次提出，主要针对单静态互易性条件下天线的最优极化[11].1970 年，Huynen 等人在Kennaugh理论的基础上提出了雷达目标唯象学方法,并利用Poincaré极化球和Stokes 矢量来表征电磁波的极化状态，提出了目标特征极化的“极化叉”概念[12].20世纪90 年代，Boerner 等人将目标最优极化的概念扩展到双静态、非互易以及非相干的情况[13].随后，Yamaguchi 等人针对特征极化开展了深入研究[14-15]，使得目标最优极化的理论不断完善.

对于一个具有对称完全相干的散射矩阵目标，可以得到与其对应的5 组特征极化状态：一组使共极化通道下雷达接收功率为零的共极化零点(Co-Pol Null)、一个使共极化通道下雷达接收功率最大的共极化最大值点(Co-Pol Max)和一个使共极化通道下雷达接收功率达到临界值的共极化鞍点(Co-Pol Saddle)、一组使交叉极化通道下雷达接收功率最大的交叉极化最大值点(X-Pol Max)、一组使交叉极化通道下雷达接收功率达到临界值的交叉极化鞍点(X-Pol Saddle)以及一组使交叉极化通道下雷达接收功率为零的交叉极化零点(X-Pol Null).由于交叉极化零点与共极化极值点在Poincaré球上位置相同，因此在Poincaré球上一共可以表示出4 组特征极化状态的位置.Boerner 等人根据这4 组特征极化在Poincaré球上的分布关系，提出了“极化树”的概念[13,16].在此基础上，清华大学杨健等人研究了特征极化状态在Poincaré球的几何位置关系并发展了利用Kennaugh矩阵和Stokes 矢量求解特征极化状态的方法，提出了等功率曲线的概念[17-19].在这5 组最优极化状态中，共极化零点又称零极化，是特征极化中最重要的一种，在目标最优极化中占有相当重要的地位.利用一对共极化零点可以恢复出除绝对能量之外的散射矩阵的全部信息，也就是说可以利用共极化零点来重建散射矩阵.20 世纪90 年代初，杨健等人将零极化理论扩展到交叉极化通道以及匹配极化通道[17].并在此基础上，考虑收发极化天线相互独立的情况，提出了目标共零及目标共零空间理论[18].目前为止，关于零极化的研究主要集中在基本概念和理论推导等方面[17,20-22]，而零极化在人造目标散射结构辨识方面的应用研究相对较少.

散射结构的辨识主要通过分析其散射机理来进行.而在散射机理分析的主流方法中，极化目标分解方法是最常用的途径，其将目标散射中心识别成不同的典型几何结构.主要采用的是相干分解方法：Pauli 分解[23]、Krogager 分解[24]和Cameron 分解等[25-27].现有研究主要是利用相干分解方法，对车辆、舰船等人造目标的散射机理进行研究.Pauli 分解将散射矩阵分解为各Pauli 基矩阵的加权和，4 种Pauli 基矩阵分别对应奇次散射、方位角为0°和45°的偶次散射和不对称分量；Krogager 分解将目标分解为球散射、旋转的二面角散射与螺旋体散射3 种具有物理意义的相干分量之和；Cameron 分解将目标极化散射矩阵依次分解成互易与非互易分量，对称与非对称分量，并将最大对称分量进行分类，主要包括二面角、三面角、偶极子、圆柱体、窄二面角、1/4 波器件等6 种散射结构.Margarit 等人利用Pauli 分解和 Krogager 分解方法分析了船舶结构与极化散射特征之间的联系[28].Fuller 等人将 Krogager 分解与 GTD 模型的频率依赖因子结合，对典型几何结构进行了细致划分，实现复杂目标中各种典型几何结构的类型判定[29].Saville在其研究基础上，利用10 类车辆目标的电磁计算数据进行识别实验，实现了不同车辆目标的识别[30].除了基于极化分解方法对散射中心的结构类型进行判别外，杨健等人定义了两个散射矩阵之间的相似性参数[31]，通过计算任意目标与特定结构之间的相似性参数，可以实现对目标结构类型的判定[32].

某种确定散射结构的零极化可以使对应的散射矩阵的接收功率为零，而对于其他散射结构，该零极化并不能使其接收功率产生明显下降，零极化具有很好的散射结构辨识的特异性.本文提出了一种人造目标散射结构零极化辨识方法，利用不同典型散射结构的零极化响应，得到零极化响应特征矢量，分析不同散射结构与典型散射结构的零极化响应特征之间的差异，识别出散射矩阵的散射类型，从而可以实现目标散射结构辨识.

1 目标零极化三维响应特征图

1.1 目标零极化与最优极化的关系

在水平和垂直极化基 (H,V)下，极化雷达获取的目标全极化信息可以由极化散射矩阵表征：

式中：SHV是垂直极化发射、水平极化接收的后向散射系数；SVH、SHH和SVV的定义类似.用ht表示发射天线的极化状态，hr表示接收天线的极化状态[1]，则雷达的接收功率可以表示为

该接收功率也被称为该极化状态对应的极化响应.其中，收发天线的极化状态均可以表示成复极化比ρ的形式：

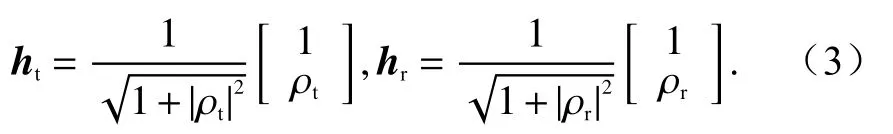
通过改变收发天线极化状态可以使雷达接收功率为零或最大，这样的收发天线极化状态称为目标的最优极化.当收发天线的极化比满足ρr=ρt=ρ时，得到共极化接收功率Pco(共极化响应)为

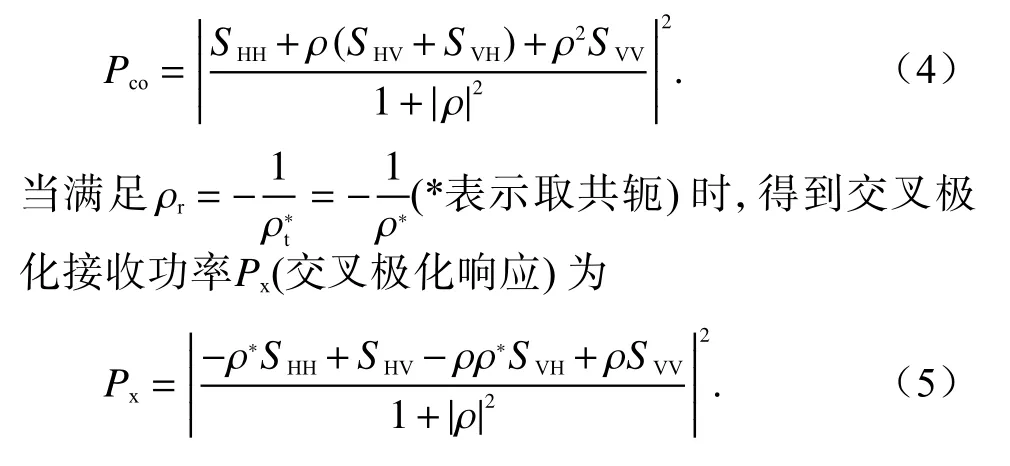
由式(4)和(5)可知，Pco和Px都是关于极化比 ρ的复变函数.通过函数的极值理论，求解Pco和Px关于极化比ρ的函数一阶导和二阶导，可以得到共极化功率的4 个稳定点以及交叉极化功率的6 个稳定点：

1) 共极化零点(Co-Pol Null)

2) 共极化鞍点(Co-Pol Saddle)

3)共极化最大值点(Co-Pol Max)

{ρcm|Pco→max}；

4)交叉极化零点(X-Pol Null)

{ρxn1,ρxn2|Px=0}；

5)交叉极化鞍点(X-Pol Saddle)

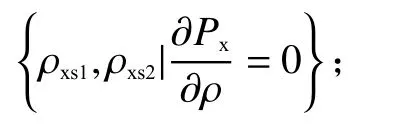
6)交叉极化最大值点(X-Pol Max)

{ρxm1,ρxm2|Px→max}.

式中，ρxn1=ρcm,ρxn2=ρcs即共极化最大值点和鞍点与交叉极化零点重合.因此，一共有4 组特征极化状态可以分别在Poincaré球上表示出来，如图1 所示.图中黑色实心点表示特征极化的位置，红色点表示的是共极化零点的位置.如图加粗的实线所示，共极化零点、共极化鞍点和共极化最大值点构成了“极化叉”.

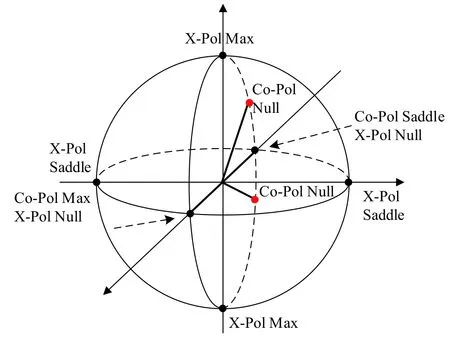
图1 目标最优极化在Poincaré 球上的位置Fig.1 The location of target optimal polarization on the Poincaré sphere

共极化零点又称目标零极化点，是目标最优极化中一种最重要的极化状态.根据Poincaré球上最优极化的分布情况可以看到，4 组最优极化状态中，两个共极化零点的位置关于共极化最大值和共极化鞍点连线(交叉极化零点的连线)对称；交叉极化最大值的连线与共极化零点的连线平行，并且是一条经过球心的直径；而交叉极化鞍点的连线既垂直于共极化零点的连线，又垂直于交叉极化零点的连线.4 种最优极化的位置均可以通过共极化零点的位置推导出来[17,19,22-33].

1.2 典型散射结构零极化矢量和零极化三维响应特征图

在给定极化基以后，电磁波的极化状态可以完全由其复极化比 ρ表征.在极化比的实部和虚部组成的二维平面内，所有的极化状态均可以和复极化比平面内的点相对应[1].设复极化比平面上任意一点P=x+jy，则可定义

其中，x,y∈(-∞,+∞)，复极化比平面为无限平面.

根据极化表征理论及其数学推导[1]，某一极化在Poincaré球上的位置和复极化比平面的位置是一一对应的.相比于利用Poincaré球来表征目标最优极化状态，本文采用复极化比平面的表征方式，将各种极化状态对应的极化响应与复极化比平面进行结合，可以更加直观地反映共极化响应随极化状态变化的情况.我们把复极化比平面上目标共极化响应的三维表征形式称作“零极化三维响应特征图”.

为了分析典型散射结构的零极化及其三维响应特征图的差异，本文选取了人造目标中的典型散射结构，如：二面角、三面角、1/4 波器件、偶极子、螺旋散射结构等，求解得到他们的零极化矢量和极化比如表1 所示.可以看出：一个散射矩阵具有两个零极化，其极化比一般是互为相反数的关系；不同散射结构的零极化矢量和极化比具有显著的差异.

表1 典型散射结构的零极化矢量和极化比Tab.1 The Null-Pol ratio and Null-Pol vector of canonical scatters

图2展示了目标的10 种不同散射矩阵在复极化比平面 (Re(ρ)∈[-3,3],Im(ρ)∈[-3,3])的零极化三维响应特征图.零极化三维响应特征图上半部分是一个三维平面，显示了各种极化状态对应的共极化响应，以“dB”形式进行展示.下半部分显示了三维平面在复极化比平面的二维投影.

图2 10 种典型散射结构的零极化三维响应特征图Fig.2 The Null-Pol 3D response pattern of 10 typical canonical scatters

从这些典型散射结构的三维响应特征图可以看到，散射结构的共极化响应均只在零极化所在的位置达到最小值，呈现“凹口状”，凹口最低点接近于零，远小于其他位置的接收功率，且凹口较窄.不同散射结构的凹口出现的位置具有显著的差异.其中，水平偶极子的零极化极化比为 ∞，且在0的位置响应最强，因此在图示的平面区域内，零极化响应呈下降趋势.垂直偶极子和水平偶极子的极化响应特征相反，零极化位于极化比等于0 的位置.左螺旋和右螺旋散射结构的零极化分别与三面角的两个零极化对应，但是螺旋散射结构在未归一化之前本身的强度稍高于三面角.

2 散射结构的零极化辨识方法

2.1 零极化响应特征矢量分析

不同散射结构的零极化可以使相应的散射结构的极化响应变为零.由图2 可以看到，零极化具有很强的散射结构辨识特异性，只有作用于对应的散射结构才能使其极化响应显著降低或者降为0.本文选取了8 种典型散射结构：三面角、二面角、圆柱体、窄二面角、1/4 波器件-1/2、水平偶极子、垂直偶极子、左螺旋和右螺旋进行分析.每种散射结构对应的散射矩阵均有两种零极化，而左螺旋和右螺旋散射结构对应的零极化分别和三面角的两个零极化相同.因此，典型散射结构对应的零极化矢量一共有14 种，分别是：三面角零极化 (h1,h2)；二面角零极化(h3,h4)；圆柱体零极化 (h5,h6)；窄二面角零极化(h7,h8)；1/4 波器件零极化 (h9,h10,h11,h12)；偶极子零极化 (h13,h14).

将每种零极化对应的极化响应Pnull称为零极化响应，用来分析不同散射结构的差异.针对某一特定的散射结构，选用不同典型散射结构的零极化hn(n=1,2,…,14)，可以得到对应的零极化响应典型散射结构的10种散射矩阵的不同零极化响应构成10 个不同的零极化特征矢量Um(m=1,2,…,10)，对其进行归一化处理，并用条形图显示，如图3 所示，图中横坐标表示14 种典型散射结构的零极化矢量的序号，从左到右分别是h1～h14；纵坐标表示零极化对应的极化响应特征.可以看到，所有散射结构均只在对应零极化的位置为零，并且在其他零极化对应的零极化响应具有显著差异.其中，三面角和二面角类似，除对应的零极化位置极化响应为零外，由于三面角和圆柱体、二面角和窄二面角的相似性，分别在圆柱体和窄二面角位置出现显著下降，其他位置均为1.圆柱体和窄二面角对于不同零极化的极化响应特征差异较大，均只在垂直偶极子零极化的位置为1.1/4 波器件、偶极子等散射结构的极化响应特征对于不同零极化的差异较小，而两种螺旋散射结构的极化响应特征分别在三面角的两个零极化位置为零，同时在圆柱体的零极化位置取值较低，其他位置极化响应较高.

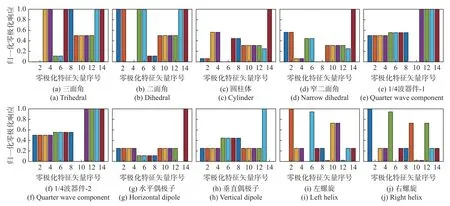
图3 8 种典型散射结构的零极化响应特征矢量Fig.3 The Null-Pol response characteristic vector of 8 typical canonical scatters

2.2 零极化散射结构辨识方法

根据2.1 节的分析可知，零极化响应特征对典型散射结构具有较好的区分效果，可以用来实现散射结构的辨识.本文提出一种人造目标散射结构零极化辨识方法，通过不同散射结构的零极化散射特征差异来区分其散射类型，方法流程图如图4 所示.

图4 零极化散射结构辨识方法流程图Fig.4 The flowchart of Null-Pol scattering structure recognition method

本方法主要针对非相干目标，一般认为目标的极化散射矩阵S描述了单一散射目标的电磁散射特性.

首先，由于目标总的电磁散射特性可以认为是强散射中心的电磁散射合成，在极化雷达图像中，利用散射中心提取方法得到目标的强散射中心位置及其散射矩阵.本文采用常用的基于散射强度的散射中心提取方法，认为雷达图像中强度相对较大的点为目标的散射中心.由于实际目标的姿态变化和观测位置的差异，会产生绕雷达视线方向的旋转.因此，为了更好地将实际目标与标准散射结构进行匹配，本文利用极化散射矩阵的旋转补偿来消除目标旋转带来的影响.假设目标的极化方位角为θ，极化旋转补偿的操作可以表示为

式中，

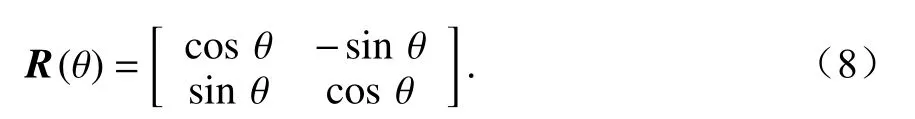
然后，根据2.1 节分析，本方法选取8 种典型散射结构的14 种零极化：三面角零极化、二面角零极化、圆柱体零极化、窄二面角零极化、1/4 波器件零极化、水平偶极子和垂直偶极子零极化.对于所有散射中心对应的散射矩阵，由式(2)可以得到其零极化响 应Pnull.假设第k个散射中心的特征矢量为Vk(k=1,2,...,Ns)，Ns为 散射中心的个数，则V k可以表示为

为了分析散射中心和典型散射结构之间的散射特性差异，将散射中心和典型散射的零极化特征矢量的差的二范数作为二者之间的距离.设第k个散射中心和第m个 典型散射结构之间的距离为dm，则

式中，m=1,2,...,10，对应8 种基本散射结构的10 个散射矩阵.因此，根据最近距离的原则，

可以得到第k个散射中心对应的散射结构类型Ik.根据上述步骤处理所有的强散射中心就可以得到所有散射中心的散射类型，从而实现目标的散射结构辨识.

3 人造目标散射结构零极化辨识实验

3.1 车辆目标散射结构辨识结果分析

本节采用美国空军实验室(AFRL)公布的CVDomes 电磁仿真数据[34]，散射结构辨识对比实验包含10 种不同车辆的电磁计算数据.CVDomes 数据的主要仿真参数如表2 所示.10 种车辆模型如图5 所示.10 种车辆模型涵盖了轿车、SUV、货卡车、旅行车、厢货车等多种类型，1993 Jeep、1999 Jeep 属于典型的SUV，Nissan Sentra、Honda Civic4dr 是小型轿车的典型代表，Toyota Camry，Toyota Avalon 属于典型的中型轿车，Nissan Maxima 属于典型的大型轿车，Toyota Tacoma 属于大型的货卡车，Mazda MPV 是典型的多功能旅行车，Mitsubishi 属于中型的厢货车，研究的范围基本包含了常用车的种类.从10 种车辆的散射结构辨识结果中选取具有代表性的4 组结果进行展示，分别是Camry、Maxima、Sentra 和Mazda MPV.零极化散射结构辨识结果和Cameron 分解的结果如图6 所示.

表2 CVDomes 数据主要参数Tab.2 The parameters of CVDomes Data

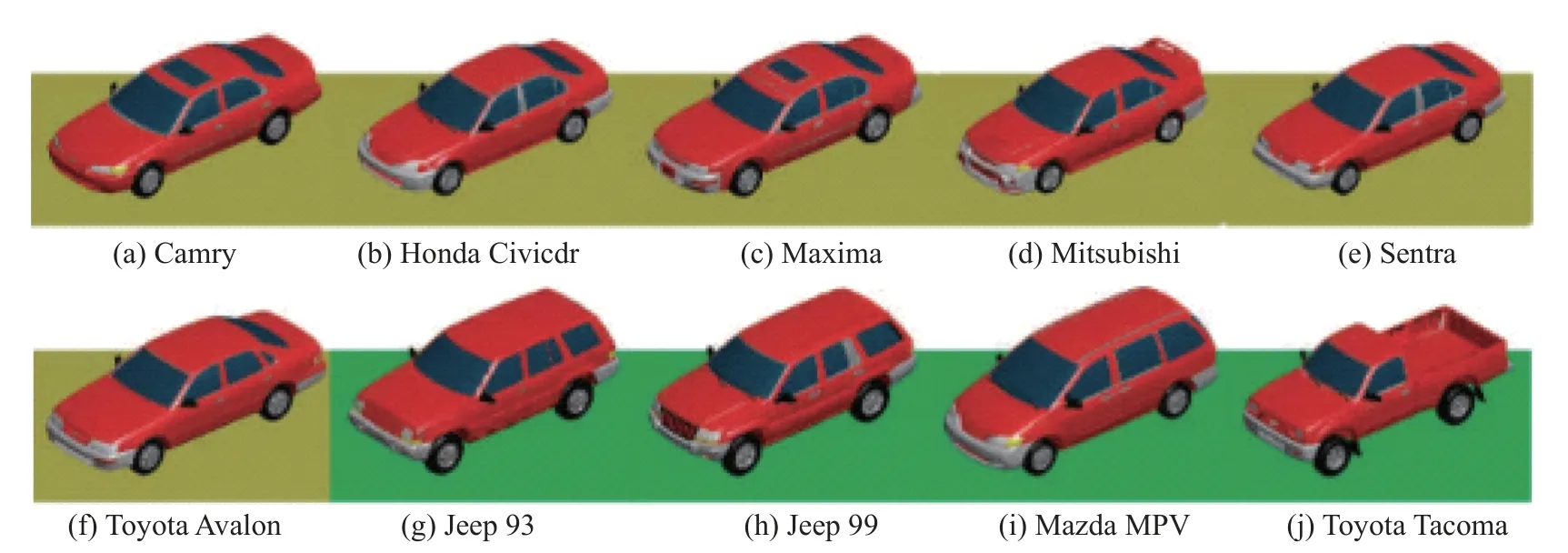
图5 10 种不同车辆目标模型示意图Fig.5 Ten vehicle models of CVDomes

从图6 可以看到成像时，由于叠掩现象的存在，车辆目标由两圈轮廓组成，其中外轮廓主要是由于车顶反射的回波先到达雷达接收端，在成像结果中相对于车轮所在的内轮廓更加靠近外侧.在散射结构辨识结果中，4 种车辆的外轮廓均正确识别为三面角/平板；而内轮廓的散射结构相对复杂，不同车辆的差异较大.对于车辆目标Camry，内轮廓主要散射结构为车身和地面形成的二面角和窄二面角结构，车身反光镜和车窗等位置形成了偶极子以及圆柱体等散射结构，零极化散射结构辨识结果和Cameron 分解结果基本相似，二者的主要差异位于车身前侧车灯位置，零极化散射结构辨识方法能够正确将其识别为圆柱体结构，并且与下侧的圆柱体结构相对称，如图6(b)中红色椭圆标注位置.Maxima车辆目标车型与Camry 相似，零极化散射结构辨识结果与Cameron 分解结果的差异也主要存在于车身前侧位置.对于车辆目标Sentra，两种散射结构辨识结果几乎相同，两者差异主要位于前后两侧车窗的位置，如图6(f)所示，零极化散射结构辨识方法的结果对称性更强，并且其识别结果更加接近实际散射结构类型.相比于前3 种小型轿车，Mazda MPV车辆目标尺寸更大，车身后侧与小轿车具有显著差异，从散射结构辨识结果来看，Cameron 分解结果中车身后侧主要为圆柱体和偶极子，而在零极化散射结构辨识中，两侧对称位置的偶极子被识别为窄二面角结构.在车身前侧，Cameron 分解中与二面角结构对应位置出现了螺旋散射结构，在零极化散射结构辨识中正确识别为二面角结构.综上，零极化散射结构辨识方法能够准确识别车辆目标中大部分散射中心的散射结构，并且相对于Cameron 分解，识别结果具有更强的对称性，更符合散射中心的实际散射类型.

图6 不同车辆目标零极化散射结构辨识结果和Cameron 分解结果Fig.6 The results of Null-Pol scattering structure recognition and Cameron decomposition for CVDomes

3.2 无人机目标散射结构辨识结果分析

为进一步验证方法的性能，本实验采用了一个全金属无人机模型的电磁计算数据.无人机模型如图7(a)所示.电磁仿真的中心频率为10 GHz，带宽为4 GHz，仰角设置为0°，方位角为0°，即正对无人机机头方向入射.Pauli 合成图如图7(b)所示.可以看到无人机的散射主要由一个个单独的强散射点组成.零极化散射结构辨识结果和Cameron 分解的结果如图8 所示.

图7 无人机模型和Pauli 合成图Fig.7 The model and Pauli image of UAV target

从图8 可以看到，两种方法对机翼和机头的解译结果基本相似，机翼均为圆柱体散射结构，机头由圆柱体和窄二面角组成.两种方法的主要差异位于机身和机翼的连接处以及机翼下方的挂载，如图8(a)中红色椭圆标注的位置.从Cameron 分解结果中可以看到，机翼与机身的连接处有一个散射中心被解译成1/4 波器件，而在零极化散射结构辨识结果中解译为窄二面角，与右侧对称位置的散射中心散射机理相同，并且更接近机翼与机身连接处的实际散射类型.除上述位置之外，两种结果在尾翼处也存在差异.尾翼处主要由偶极子、窄二面角和圆柱体等结构组成，Cameron 分解中存在部分1/4 波器件等复杂散射机理，而零极化散射结构辨识结果中不存在复杂结构，且左右两侧对称性更强.由于尾翼包含螺旋桨等复杂散射结构，散射机理本身比较复杂，针对尾翼散射机理的准确解译有待研究.总体而言，零极化散射结构辨识的结果与Cameron 分解结果性能相当，主要散射结构均能够正确解译，并且在部分明显结构处具有显著优于Cameron 分解的性能.

图8 无人机零极化散射结构辨识结果和Cameron 分解结果Fig.8 The results of Null-Pol scattering structure recognition and Cameron decomposition for UAV Target

4 结论

零极化是目标最优极化的重要组成部分，可以反演出其余的最优极化状态.本文从目标结构辨识角度，首次揭示了零极化理论方法在人造目标散射结构辨识方面具有独特优势；并提出了一种零极化三维响应特征图的可视化表征方法.通过复极化比平面的表征方法与极化响应特征相结合，可以更加直观清晰地展示不同散射结构的零极化差异，从而揭示了典型散射结构的三维响应特征图的差异及零极化在区分不同散射结构方面的潜力.本文还提出了一种人造目标散射结构的零极化辨识方法.通过提取极化雷达图像中人造目标的强散射中心，分析强散射中心和典型散射结构之间的零极化响应特征差异，构建距离度量，根据最小距离分类原则，识别出散射中心的散射结构类型.利用车辆和无人机目标的电磁仿真数据开展了散射结构辨识实验.结果表明，本文提出的零极化散射结构辨识方法能够准确识别出常见的车辆和无人机目标散射结构类型，且散射结构辨识结果相对于Cameron 分解具有更优的性能.

下一步的研究工作将重点围绕目标几何结构反演和三维重构进行：一方面，结合零极化目标散射结构辨识结果建立新的可视化表征方法，反演出目标的真实结构；另一方面，利用多视角等复杂雷达数据，提取目标三维信息，结合零极化方法开展复杂结构目标三维辨识.