一种联合地基GNSS 和测高仪数据的电离层层析成像新算法

欧明 吴家燕 陈龙江 甄卫民 吕梦海

（1.中国电波传播研究所，青岛 266107；2.中电科(青岛)电波技术有限公司，青岛 266107）

引言

电离层是指地球上空60～1 000 km 高度大气电离区域，穿越该区域的无线电波会产生折射、反射、散射和吸收等效应，从而影响导航、通信、测控、遥感等诸多无线电信息系统的性能[1].利用各类技术手段来获取电离层的特征参量，研究电离层中的各种现象，从而揭示其背后的物理机制，具有重要的科学乃至政治、军事和经济意义[2].电子密度是表征电离层状态最为直接的特征参量之一，获取精确的电子密度变化即可量化电离层对卫星导航、通信、雷达的影响[3-4].

电离层层析成像(computerized ionospheric tomography,CIT)是随着计算机硬件性能的提升和卫星电离层探测的进步而逐渐发展起来的一种非常重要的电离层遥感工具.CIT 是利用卫星测量的电离层积分总电子含量(total electron content,TEC)反演得到电子密度的过程[5].目前CIT 主要数据来源包括低轨卫星信标、中高轨GNSS 数据，而早期CIT 数据来源主要是低轨信标[6].近年来基于地基GNSS 台站进行CIT 是主要的发展方向，国内外研究人员利用GNSS 三维CIT 技术，获取了大量电离层水平、垂直方向的结构信息[7].

受限于扫描视角和台站数目非均匀分布的影响，基于地基GNSS 数据的CIT 算法不同程度存在着电子密度成像垂直分辨率不高的问题[8-9].近年来，多手段联合CIT 技术开始成为世界各国的研究热点.Hajj 等提出了联合地基和天基观测反演电离层电子密度(ionospheric electron density,IED)的设想[10]；Rius等尝试了地基GPS 数据和MET 卫星掩星数据的CIT 试验[11]；Dear 等提出采用地面测高仪优化GPS 数据实现IED CIT[12]；英国Bath 大学开发了多手段数据分析软件(multi-instrument data analysis system,MIDAS)，利用模式化基函数(球谐函数与经验正交函数)进行电离层表征，同时利用奇异值分解(singular value decomposition,SVD)的方法对表征函数的权重进行求解，以降低CIT 反演过程中由于数据稀疏性造成的矩阵求逆困难[13-14].为了提高三维CIT 的稳定性，Ma 等提出利用测高仪联合GPS 观测，结合神经网络的方法获取三维电子密度[15]；Yao 等提出了组合型CIT 算法，以解决单独使用函数基CIT 模型和像素基CIT 模型存在的阶数选择困难、反演参数多、计算效率低的问题[16].肖锐选择经验正交函数(empirical orthogonal function,EOF)作为三维时变CIT 算法的基函数，从而大大降低了三维CIT 需要求解的未知数数量，提升了算法的稳定性和时效性[17]；闻德保针对GPS 基CIT 中的不适定问题，先后提出了多种解决方案，如选权拟合法等[18]；Li 等提出了一种新CIT 方法，旨在通过使用受约束的最小二乘来缓解CIT 矩阵的不适定问题，以提高IED 的反演精度[19]；Ssessanga N 等通过将测高仪数据结合同化技术中，以提高CIT 的稳定性并避免电子密度反演过程中的负值问题[20].由此可以看出，联合多种手段观测数据已成为提升CIT 分辨率的主要方法.

本文针对目前地基GNSS CIT 存在垂直分辨率较低和算法稳定性不足的问题，提出了一种联合地基GNSS 和测高仪数据的三维CIT 新算法，该算法综合了GNSS 电离层探测水平分辨率较高和测高仪电离层垂直探测分辨率较高的优点，以全球电离层无线电观测网(global ionospheric radio observatory,GIRO)测高仪数据驱动更新IRI 模型，将驱动后的IRI 模型作为背景电离层模型，再利用改进的代数重建迭代(algebraic reconstruction technique,ART)算法进行CIT，有效提升了电离层三维电子密度重构的精度，相比仅利用地基GNSS 数据，该算法电离层hmF2的反演精度明显提升，通过实测数据对本文算法的精度进行了验证.

1 CIT 算法

1.1 CIT 原理

三维CIT 主要是指通过一系列卫星和地面接收机间无线电信号传播路径上的积分TEC 测量来重构区域内三维的IED 分布.地面GNSS 接收机所获得的TEC 可以表示为沿信号传播路径上电子密度的积分，即：

式中：di为总电子含量；i为射线编号；Ne(r)为沿传播路径随空间r变化的电子密度；S为地面接收机至卫星的视线路径.

将反演区域按照经度、纬度和高度方向划分为N个网格，采用级数展开型算法，利用一组空间基函数hk(r)将电子密度分布离散化，有：

式中：K表示展开所取的级数；ak为权重系数.由于ak不随时间变化，有：

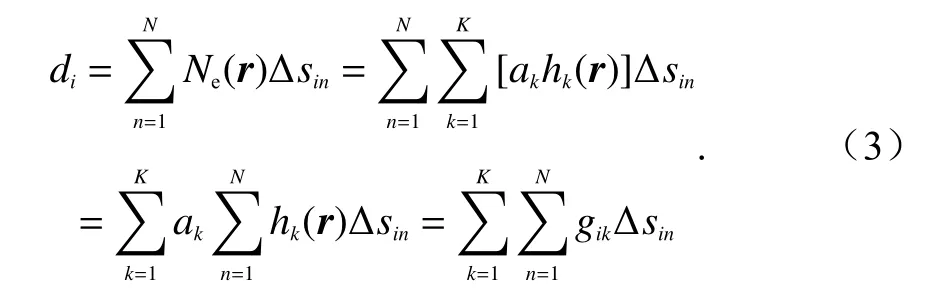
式中：Δsin表示第i个射线在第n个网格内的截距；gik由 权重系数ak与基函数h k(r)相乘得到.

在给定基函数的具体形式后，根据相应射线的几何位置可以确定gik.基函数包括像素基函数和函数基函数两大类.本文采用像素基函数，其将空间离散为有限数目的网格，且将网格中的电子密度当作常数分布.若网格内有无线电信号传播路径通过，则基函数设定为1，否则为0，即：

因此，电离层问题可以转换为求解下列线性方程组的问题：

式中：向量d由TEC 观测数据di组成；采用像素基函数后，待求量X即为电离层电子密度Ne；投影矩阵A由基函数加权的第i条信号传播路径在第j个网格内投影相对于参考路径的增量gik组成.采用CIT 算法求得基函数权重，便可得到电子密度的分布[21].

1.2 改进的ART 算法

CIT 方程组，即式(5)的求解，目前常用的算法为ART 算法.ART 算法对初始估计反复进行迭代修正，直到某种设定的条件得到满足为止，每一次修正针对一个方程进行.这类算法比较节省计算机内存资源且易于操作，应用较为广泛[6].算法的计算流程如下：

1)首先设定电离层模型背景场初值X(0)，且

2)基于实测的电离层数据，背景场初值按照以下迭代方式求解 ：

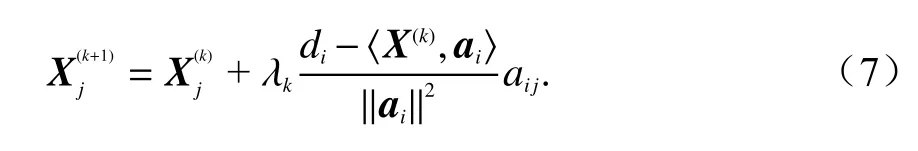
式中：j为网格编号；分别为迭代k+1 次和k次的第j个网格的电子密度；λ为松弛因子；aij为第i条路径在第j个网格内的投影；‖ai‖为第i条路径总长.

由式(7)可以看出，ART 算法迭代过程中，方程的迭代顺序、迭代轮次、松弛因子的具体取值均会对CIT 的最终结果造成一定的影响.松弛因子与ART 算法的收敛速度直接相关，其取值影响收敛时的震荡幅度和收敛所需的迭代次数.

传统ART 算法松弛因子取一个固定常数，迭代顺序如何给定等方面存在较大的随意性，使得CIT 结果存在稳定性较差的问题.为消除算法的不稳定性，本文对ART 算法进行相应的改进，具体实现方法如下：

1) λk采用与迭代轮次k相关的函数，使得迭代松弛因子能够随着迭代轮次的增加而逐步降低，从而保证迭代收敛的稳定性，设定方法如下：

2)设置迭代截止门限 tol，当 tol＜10-8时停止迭代，门限值计算方法为

3)改进ART 算法的迭代顺序，算法不再按照i=mod(k,m)+1的顺序进行迭代，而是采用随机数的方法确定迭代顺序，以消除传统ART 算法采用固定迭代次序对电子密度反演精度的影响.

4)网格内同一高度层的电子密度加入水平约束，以实现对无射线穿越网格内电子密度的调整.水平约束采用双线性插值算法实现：

式中：w表示双线性插值所用的加权系数，其实现方法可参考文献[22].

1.3 测高仪数据驱动的电离层背景场初值

背景场初值对三维CIT 的结果影响非常大，给出一个更为合理的背景初值将在一定程度上提高CIT 的精度.传统的CIT 方法一般选择经验电离层模型输出的电子密度值作为背景场，其中最为常用的模型即国际参考电离层模型IRI[23].由于地基GNSS用于三维CIT 的垂直分辨率较低，利用测高仪数据数据驱动IRI 可在高度方向上提升地基GNSS 三维CIT 的分辨率[24-25].

IRI 模型基于CCIR/URSI 系数计算全球电离层F2层特征参数foF2和hmF2.本文利用GIRO 发布的测高仪自动判读数据，通过分步线性最优估计方法更新CCIR/URSI 系数[26]，使得IRI 模型计算的电离层foF2和hmF2与测高仪观测数据之间的方差最小，进而获得更准确的全球电子密度分布作为CIT 的背景初值.分步线性最优估计具体的实现方法可参考文献[26].

2 数据来源

2.1 GNSS 数据

选择中国及周边区域约290 个地基GNSS 台站的数据参与CIT，数据由IGS 和中国陆态网获得，台站的地理位置分布如图1 所示，其中红色实心方块为地基GNSS 台站.

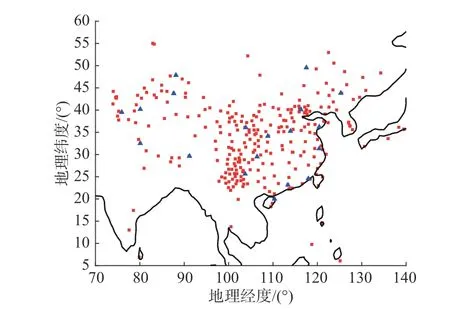
图1 CIT 使用的地基GNSS 台站(红色方块)和精度评估用的测高仪台站(蓝色三角)分布Fig.1 Distributions of ground-based GNSS stations (red□) for CIT and ionosonde stations (blueΔ) for accuracy validation

在进行CIT 反演之前，首要的任务是利用地基GNSS 观测文件获取电离层TEC 信息.在计算TEC前，首先利用Bernese 软件对RINEX 文件进行数据预处理.Bernese 软件是瑞士伯尔尼大学天文研究所针对GNSS 高精度测绘研制的一款经典软件，该软件广泛应用于GPS 数据后处理领域中[27].本文首先利用Bernese 软件对RINEX 格式文件中GNSS的观测数据进行周跳和异常值的探测，并采用双频的载波相位观测数据平滑码伪距，最后平滑处理后的观测数据仍以RINEX 格式的文件输出.这样处理可较好剔除GNSS 数据中的部分异常观测值，从而提升CIT 的质量.

利用意大利Gran Sasso 太空研究所研制的GNSS TEC 数据处理软件对各台站的RINEX 观测数据进行处理，从而计算得到电离层TEC 信息[28].GNSS_2016 软件通过读取GNSS 观测数据及相应GNSS 卫星的星历，可输出卫星编号、观测时刻、卫星仰角、方位角、穿刺点经纬度及倾斜路径上的TEC 值.

2.2 Madrigal TEC 数据

美国麻省理工大学Madrigal 能够管理和提供各种形式的存档的和实时的地球空间物理在线数据，是一个功能强大的数据库.Madrigal 采用统计框架对全球数千个地基GNSS 数据进行处理，用于估计GNSS 非电离层差分延迟偏差，实现了1°×1°×5 min 分辨率电离层TEC 的高精度估计，在空间物理研究领域应用非常广泛[29].本文选择Madrigal TEC 数据产品对CIT 重构的TEC 地图进行精度评估.

2.3 电离层测高仪数据

测高仪数据下载自全球电离层无线电观测站GIRO.GIRO 是美国马萨诸塞州Lowell 大学发起和建立的全球电离层数字测高仪站网.截止目前，GIRO的台站已经覆盖了全球27 个国家并在美国Lowell建立了一个数据处理中心LGDC，由LGDC 负责全球超过50 个测高仪台站的数据处理(电离图自动判读与数据质量控制)、建模(IRI 实时同化模型IRTAM 和全球底部电离层时效同化模型GAMBIT)，以及DIDBase 等数据产品的发布[30].电离图自动判读数据即为DIDBase 数据之一.在CIT 研究中利用GIRO 自动判读的测高仪数据对IRI 模型进行驱动，GIRO 包括了全球50 个台站的数据，其中有3 个国内台站和47 个国外台站，具体台站列表请见http://giro.uml.edu/.

同时，利用独立的中国国防电波观测站网19 个测高仪台站数据对CIT 的精度进行评估.图1 中蓝色三角形即为精度评估所用的测高仪台站的位置分布.需要说明的是，在本文电子密度精度评估时，采用全部19 个台站的数据进行foF2评估.但是考虑到目前电波观测网的测高仪的判读数据不包含hmF2，需要利用POLAN 程序通过人工判读电离图的方式处理得到，因此本文仅选择北京、苏州和海口3 个不同纬度台站的hmF2数据进行精度评估.

3 CIT 结果分析

3.1 电离层TEC 地图精度分析

CIT 算法网格划分，设定为水平方向经度和纬度上的网格大小为2.5°×2.5°，垂直方向450 km 以下高度网格间距为10 km，450～1 000 km 高度区间网格间距为25 km，时间分辨率设定为15 min.首先分析CIT 算法给出的电离层TEC 地图的重构精度.为显示方便，图2～5 分别按照1 h 时间间隔，给出了2017-09-06T00:00—23:00UT 中国及周边区域Madrigal、欧洲定轨中心CODE-GIM、IRI 模型及本文CIT 算法重构TEC 的时空分布特征.

从图2～5 的对比可以看出：相比于Madrigal 的TEC 产品，CODE 给出的TEC 分布与观测值基本形态较为符合，但磁赤道驼峰区附近的TEC 要偏低，且TEC 整体分布过于平滑，无法反映局部的TEC 中小尺度的变化特征；IRI 模型计算的TEC 则相比观测结果存在系统性偏低的情况；而本文CIT 算法重构TEC 则与Madrigal 数据非常一致，且在大部分细节结构上与Madrigal 结果类似.

图2 2017-09-06 中国及周边区域Madrigal 给出的TEC 分布Fig.2 Distribution of Madrigal vertical TEC over China and surrounding areas on September 6,2017

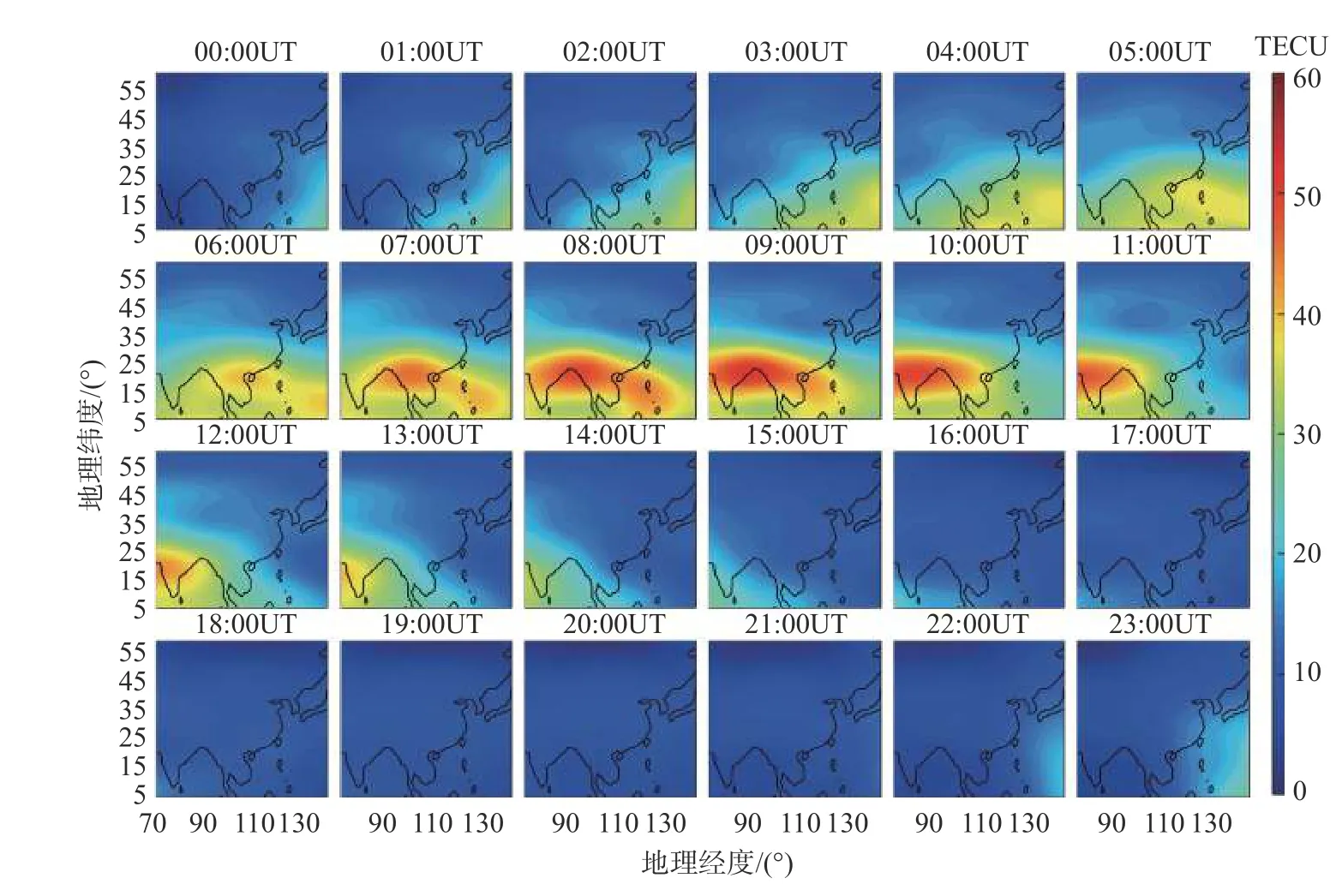
图3 2017-09-06 中国及周边区域CODE-GIM 数据给出的TEC 分布Fig.3 Ionospheric TEC distribution of CODE-GIM over China and its surrounding regions on September 6,2017

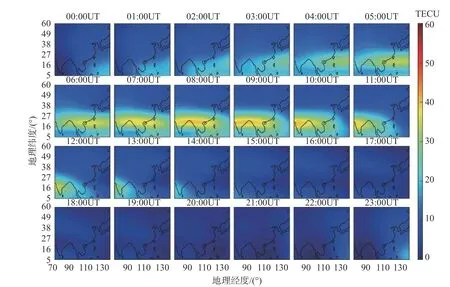
图4 2017-09-06 中国及周边区域IRI 模型计算给出的TEC 分布Fig.4 Ionospheric TEC distribution of IRI model over China and its surrounding regions on September 6,2017

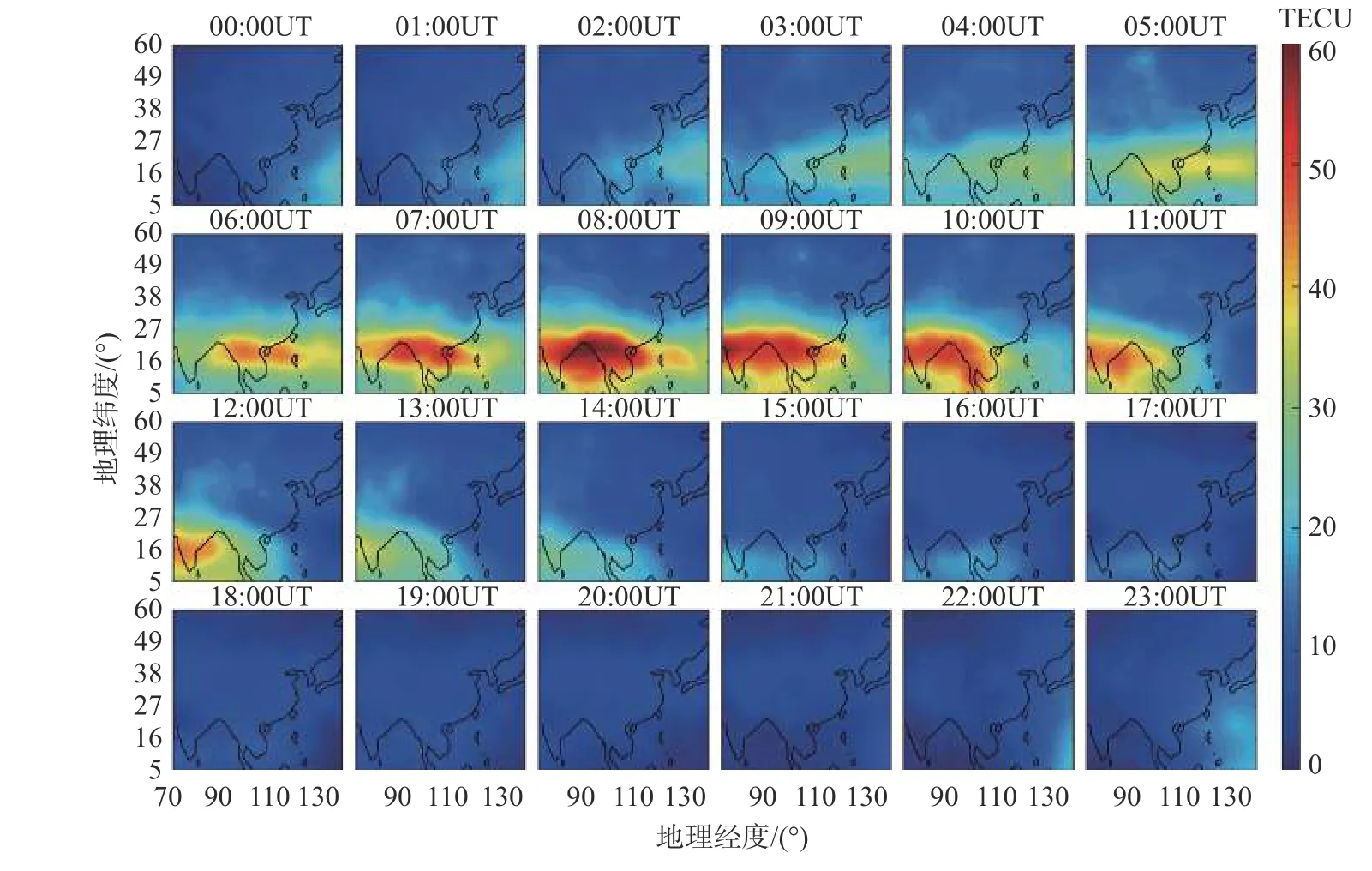
图5 2017-09-06 中国及周边区域CIT 重构的TEC 分布Fig.5 TEC distribution of CIT algorithm over China and its surrounding regions on September 6,2017

进一步地，对CODE-GIM、IRI 模型及CIT 三种方法的TEC 精度进行统计比较，评估结果如图6 所示.从分析结果来看：CODE 电离层TEC 数据相对Madrigal 数据的平均误差为4.0 TECU，标准差为3.2 TECU；IRI 模型的平均误差为2.9 TECU，标准差为4.4 TECU；CIT 算法的平均误差和标准差则分别下降为2.5 TECU 和3.0 TECU，精度提升效果非常明显.

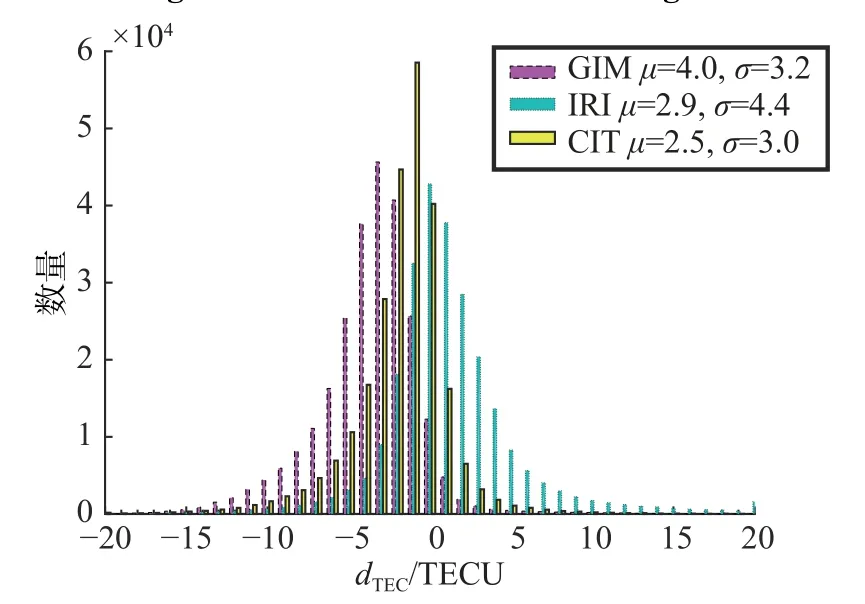
图6 电离层TEC 地图精度评估结果Fig.6 Accuracy evaluation results of different ionospheric TEC map

3.2 IED 精度分析

同样地，根据地基GNSS 和测高仪数据进行联合CIT，可以获取区域三维时变的电子密度分布.图7给出了2017-09-06T00:00UT 时刻中国及周边区域上空三维电子密度剖面.其中图7(a)所示为电子密度沿着经度面的切片；图7(b)所示为峰值电子密度；图7(c)所示为电子密度沿着高度面的切片；图7(d)所示为电子密度沿着纬度面的切片.从电子密度空间形态来看，CIT 结果较好地再现了该区域电离层随纬度、经度和高度方向的基本变化特征.同样地，图8 给出了经度100°上IED 随时间-纬度-高度上的变化.可以看出，该区域电子密度的纬度和高度变化特征基本符合电离层的基本变化规律.

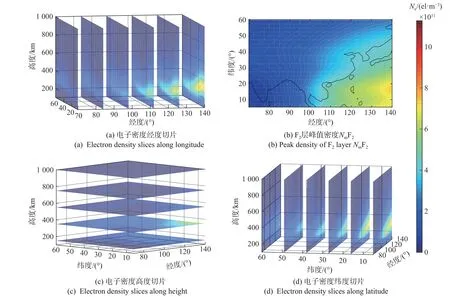
图7 2017-09-06T0:00UT 中国及周边区域上空CIT 的三维电子密度Fig.7 3D electron density distribution of CIT over China and its surrounding areas at 0:00UT on September 6,2017

图8 2017-09-06T0:00UT 经度100°上空IED 随时间-纬度-高度的变化Fig.8 The variation of ionospheric electron density over 100°E at 0:00UT on September 6,2017

进一步地，利用独立的国防电波观测站网测高仪的实测数据对CIT 前后的foF2和hmF2精度进行分析.图9 给出了CIT 前后电离层foF2精度的对比结果.CIT 前，背景模型IRI 的foF2平均误差为0.89 MHz，标准差为0.96 MHz；仅利用地基GNSS 进行CIT，其foF2平均误差和标准差分别下降为0.75 MHz 和0.7 MHz；联合GNSS 和测高仪进行CIT(GNSS＋IonCIT)，其foF2平均误差和标准差则进一步下降为0.63 MHz 和0.61 MHz.从对比结果来看，仅利用GNSS 进行层析，也能在一定程度上提高电离层foF2的精度，而联合测高仪数据后，则精度又有进一步的提升.

图9 CIT 前后电离层foF2 误差比较Fig.9 Comparison of ionospheric foF2 deviation before and after CIT

同样的，图10 给出了CIT 前后电离层hmF2精度的对比结果.从统计结果来看，仅利用地基GNSS 进行CIT，其hmF2平均误差和标准差相比背景模型几乎无明显变化，平均误差和标准差均在20.6 km 和16.5 km 上下，由此可以看出，如果仅仅考虑利用地基GNSS 进行CIT，将难以提升电子密度的垂直分辨率；而联合GNSS 和测高仪进行CIT 后，其hmF2平均误差和标准差则下降为14.8 km 和11.7 km，验证了联合测高仪数据后对CIT 精度的提升效果.

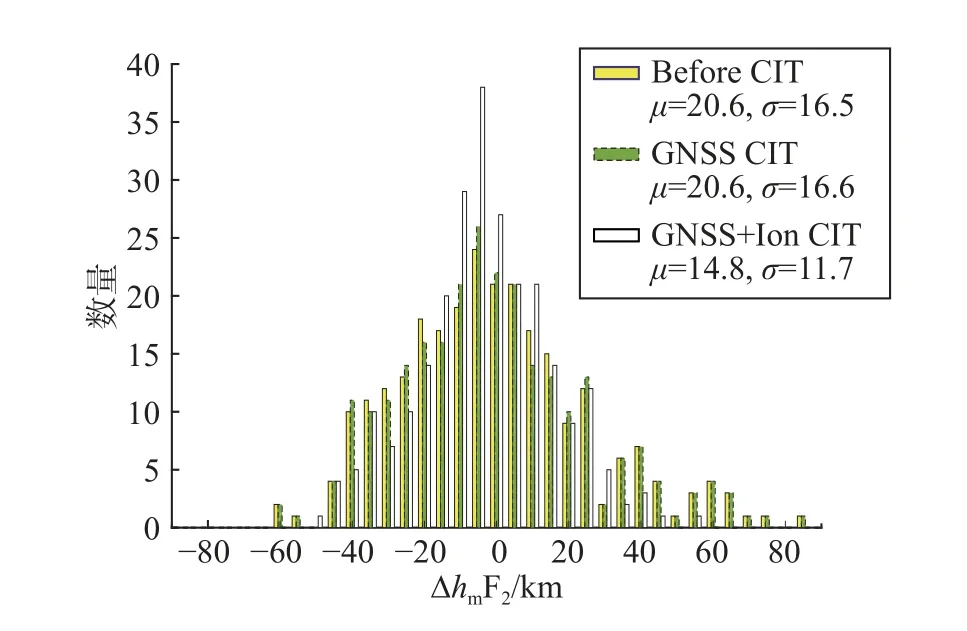
图10 CIT 前后电离层hmF2 误差比较Fig.10 Comparison of ionospheric hmF2 deviation before and after CIT

4 小 结

针对单独使用地基GNSS 进行三维CIT 的不足，提出了一种联合地基GNSS 和测高仪数据的三维CIT 方法.算法综合了测高仪探测电离层垂直分辨率较高和地基GNSS CIT 水平分辨率较高的优点，以测高仪辅助驱动更新IRI 模型，将驱动后的IRI 模型作为背景电离层模型，再利用改进的ART 算法进行CIT；基于IGS 与中国陆态网地基GNSS 台站及GIRO 测高仪数据实现了中国及周边区域三维CIT.对CIT 结果获取的TEC 和电子密度的形态学分析验证了方法的可靠性；与独立观测的测高仪数据的对比结果表明：仅依赖地基GNSS 进行CIT 无法有效提升hmF2的重构精度，联合测高仪数据进行CIT 后，电离层foF2和hmF2的重构精度均有明显提升.

需要指出的是，本文用于CIT 成像精度评估的台站主要分布于GNSS 台站较为密集的区域.对于GNSS 观测站非常稀少的区域，如海洋或者沙漠上空区域，本文CIT 成像算法的适用性还需要进一步的分析验证，这也是本文下一步的研究方向.

致谢：本文GNSS 观测数据从IGS 网站和中国大陆构造环境监测网络(crustal movement observation network of China,CMNOC)获取.全球电离层地图CODE 数据从http://ftp.aiub.unibe.ch/CODE/网站获取.麻省理工学院高精度Madrigal 数据由http:// cedar.openmadrigal.org/下载，作者在此表示感谢.