增强六手臂缺失支柱手性拉胀超材料力学性能理论研究1)

朱一林 江松辉 于 超

* (西南石油大学土木工程与测绘学院,工程安全与防护研究院,成都 610500)

† (西南交通大学力学与航空航天学院,应用力学与结构安全四川省重点实验室,成都 610031)

引言

拉胀材料是自20 世纪80 年代起迅速发展起来的一类具有负泊松比效应的功能和结构一体化的力学超材料[1-3].与传统材料相反,拉胀超材料承受拉伸(压缩)载荷时,会产生横向膨胀(收缩).这种反常规的变形行为赋予了拉胀超材料优越的力学性能,表现在抗剪切、抗压缩、抗冲击、抗断裂、抗疲劳,能量吸收和减震等诸多方面[4-8].优越的力学性能使拉胀超材料在航空航天[9-11]、军事国防[12-15]、汽车船舶[1,16]、生物医学[17-19],土木工程[5,20-22]及智能传感[23-26]等领域有广阔的应用前景,并吸引了国内外广大学者的广泛关注.

负泊松比是一个古老的研究课题.早在1848 年,法国科学家圣维南[27]就指出在各向异性材料中可能会有负泊松比存在.经过近一个半世纪的发展,尤其是自Lakes 于1987 年首次制备出负泊松比材料以来,国内外力学和材料学界迎来了对负泊松比材料的研究高潮.1991 年,Evans[28]将具有负泊松比特性的材料正式命名为“auxetics”(源自于希腊文“auxetikos”).“auxetics”后被国内学者译为“拉胀材料”.由于可呈现出天然材料所不常有的力学特性,拉胀材料又被称作“拉胀超材料”.

根据结构形式和变形机理的不同,拉胀超材料大致可归类为纤维增强层压型拉胀复合材料,拉胀纱,拉胀泡沫,拉胀折纸和拉胀蜂窝材料五种形式[6,26,29-32].拉胀蜂窝材料具有规则的元胞结构,非常便于设计、优化和制备,因此近些年得到了更广泛的关注.根据微结构的几何形式和主导的变形机理,拉胀蜂窝材料又可以进一步划分为内凹型拉胀蜂窝材料(具有内凹角,具有轴对称性质)和手性拉胀蜂窝材料(具有旋转对称性质,变形时伴随着旋转)[33-34].相较于内凹型拉胀材料,手性拉胀材料在大变形下的拉胀性能表现更好,并且可容许更大的制造误差[35-38].传统手性拉胀材料的元胞结构由中心圆环和与之相切外接组成.经典的手性拉胀材料包括传统手性拉胀材料和缺失支柱手性拉胀材料两种材料形式.根据与单个圆环连结的手臂个数及手臂与相邻两圆环的连结形式,传统手性拉胀材料包括三手臂手性、三手臂反手性、四手臂手性、四手臂反手性及六手臂手性拉胀材料[35,39-41](图1).缺失支柱手性拉胀材料可视为将传统手性拉胀材料的圆环替换为绑扎桁架而构成[34,42-48](图2).其余手性拉胀材料均可视为由这两种材料演变而成.

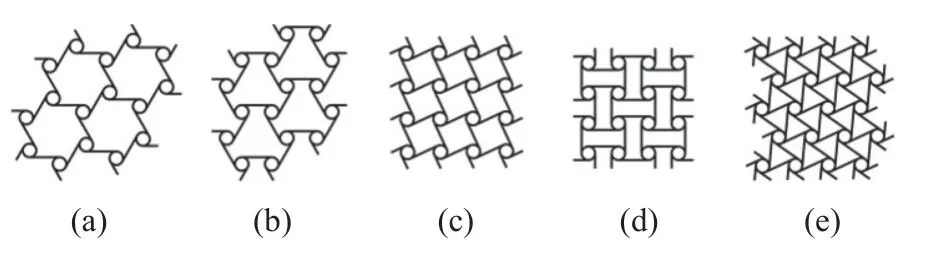
图1 传统手性拉胀材料: (a) 三手臂;(b) 反三手臂;(c) 四手臂;(d) 反四手臂;(e) 六手臂Fig.1 (a) Tri-,(b) anti-tri-,(c) tetra-,(d) anti-tetra-,(e) hexa-chiral honeycombs

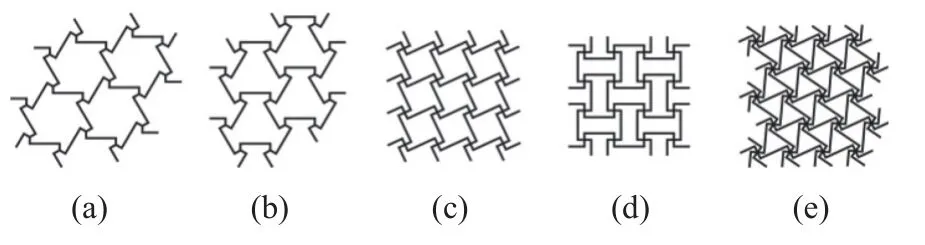
图2 缺失支柱手性拉胀材料: (a) 三手臂;(b) 反三手臂;(c) 四手臂;(d) 反四手臂;(e) 六手臂Fig.2 (a) Tri-,(b) anti-tri-,(c) tetra-,(d) anti-tetra-,(e) hexa-missing rib honeycombs

传统手性拉胀材料的拉胀效应主要源自其中心圆环的转动和手臂的弯曲.然而,已有研究表明在大变形时其中心圆环容易发生畸变,旋转效应相应减弱,进而导致拉胀性能的迅速劣化[35].因此,传统手性拉胀材料无法在大变形范围内具备恒定的负泊松比,为其实际的工程应用带来了困难.根据Simth 等[48]、Liu 等[43]以及作者团队[3,46-47]的研究表明,缺失支柱拉胀材料可以在较大的应变范围内表现出恒定的泊松比.与传统手性拉胀材料类似,缺失支柱手性拉胀材料的拉胀效应也主要源自其中心绑扎桁架的转动和手臂的弯曲.但由于组成中心绑扎桁架的梁之间缺乏支撑,初始的缺失支柱手性拉胀材料的旋转效应较弱,因而其拉胀性能也较弱.作者团队[47]在具有初始面内各向同性的六手臂缺失支柱手性拉胀材料的中心绑扎桁架中引入了简单的六边形结构支撑,发展了增强六手臂(直臂)缺失支柱手性拉胀材料(图3(a)).该拉胀材料可以在大应变范围内具有可调的恒定负泊松比.特别是,通过调整几何参数,该拉胀材料可在近30% 的应变范围内具有趋近于-1 的负泊松比.众所周知,各向同性结构材料的等效剪切模量为和分别为等效弹性模量和泊松比).因此,结构材料的负泊松比趋于-1 时,其剪切模量理论上趋于无穷大,具有绝佳的抗剪性能.从而,增强六手臂(直臂)缺失支柱手性拉胀材料具有广阔的工程应用前景.为进一步增大具有恒定负泊松比的应变范围,作者团队还进一步发展了增强六手臂(曲臂)缺失支柱手性拉胀材料(图3(b)).

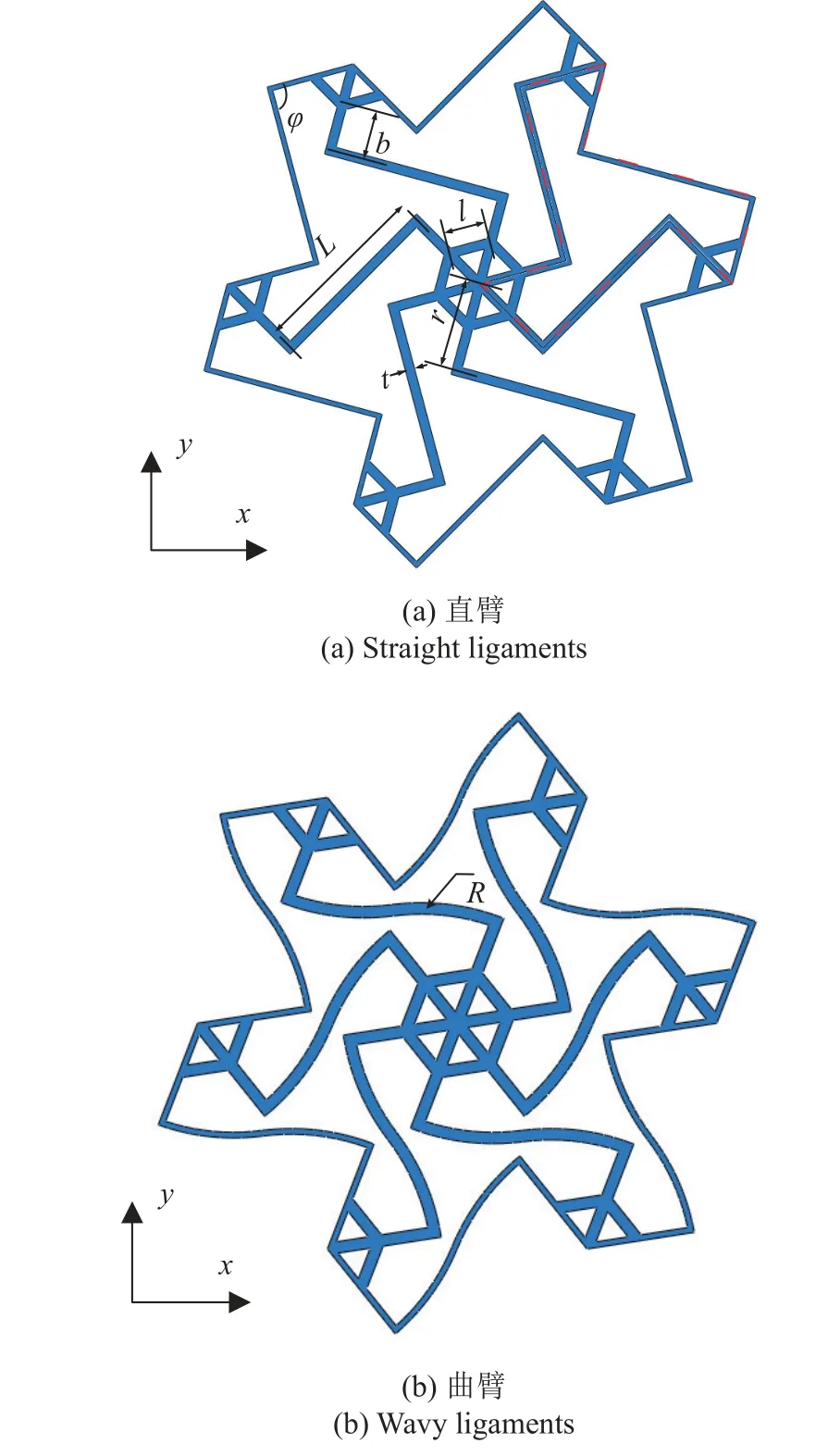
图3 增强六手臂缺失支柱手性拉胀材料元胞图Fig.3 Unit-cells of enhanced hexa-missing rib honeycomb

但作者团队的前期工作仅局限于有限元分析,缺乏对所发展的拉胀材料力学参数的理论描述,无法根据目标性能进行有效的结构参数设计,限制了其工程应用.而参数化设计有助于对超材料进行结构优化,从而促进其工程应用[49-50].本文所研究的拉胀蜂窝材料大都由细长结构组成,可被假设为欧拉-伯努利梁[51].大量研究证实利用能量法(如卡氏定理)可有效地推导拉胀蜂窝材料力学参数的理论表达式.因此,本文致力于利用能量法给出前期发展的增强六手臂缺失支柱手性拉胀材料等效弹性模量和泊松比的理论表达式,以期为拉胀材料的有效参数设计提供理论指导.

1 几何模型

增强六手臂缺失支柱手性拉胀材料为典型二维结构材料.其元胞如图3 所示,由“Z”形梁结构及增强六边形组成.元胞还可视为由六个最小代表单元(红色虚线部分)阵列而成.直臂结构的元胞几何形状可由五个独立参数确定,即“Z”形梁长手臂长度L;Z”形梁短手臂长度r;“Z”形梁内角 φ ;增强六边形结构边长l以及所有梁结构的宽度t(如图3(a)所示).由图3 可见,元胞结构的绑扎桁架由“Z”形梁短手臂及增强六边形组成,而“Z”形梁长手臂则与其相接.因此,为后续叙述方便,下文中“Z”形梁长手臂和短手臂分别记为外手臂和内手臂.

将图3(a)中的直手臂替换为等长圆弧即可得相应曲臂拉胀材料.因此,要描述曲臂材料的元胞几何形状,还需引入表征其半径的参数R.需要指出的是前述所有表征梁长度和半径的参数均沿梁中性轴测量.

为后续描述方便,本文定义了参数b来表征增强六边形与手臂之间的距离.b可由r和l表示,即

另外,本文还引入了增强率p及手臂比q分别来描述材料增强的程度及内外手臂长度的比例.p和q的表达式为

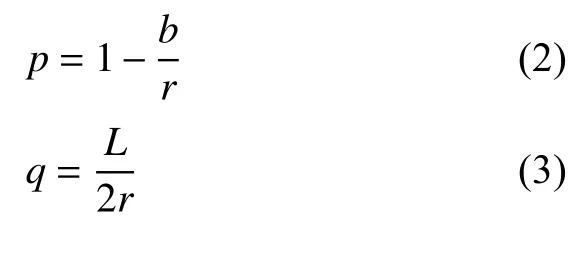
2 等效力学参数理论表达式(小变形)

如前所述,本文所研究的两种拉胀材料均可视为由多个欧拉-伯努利梁组成.因而,可利用能量法推导其等效弹性模量和泊松比.利用能量法推导等效力学参数通常的做法是: 首先,对阵列的拉胀材料施加远场应力;然后,取最小代表性单元,并根据几何和受力条件确定各梁的受力状态;最后,推导最小代表性单元的应变能,并根据卡氏定理和几何相容条件获得等效弹性模量和泊松比的表达式.

对于具有简单最小代表单元构型的拉胀材料(如最小代表单元具有三角形边界的三手臂传统/缺失支柱反手性拉胀材料,最小代表单元具有矩形边界的四手臂传统/缺失支柱反手性拉胀材料等),最小代表单元的受力状态可由几何和远场应力条件确定[3,37,46].然而,对于本文所研究的拉胀材料,其最小代表单元的边界较为复杂(图3(a)),无法通过传统方法推导其力学参数的理论表达式.Liu 等[43]发展了基于最小代表单元整体受力平衡条件和变形协调条件的方法,准确地推导了具有弱连结的六手臂缺失支柱手性拉胀材料的力学参数的理论表达式.六手臂缺失支柱手性拉胀材料与Liu 等[43]所提出的材料具有相似的构型,因此,本文将基于同样的思路来进行理论推导.

以增强六手臂(直臂)缺失支柱手性拉胀材料为例.对其施加如图4(a)所示远场拉应力,其最小代表单元的受力情况如图4(b)所示.该最小代表单元由三个增强杆和三根“Z”型梁组成.前期研究表明[3],由增强杆和“Z”型梁组成三角形单元体在结构整体变形时几乎不会发生畸变,局部应变非常小,可以视为刚体.因此,推导最小代表单元的计算应变能时,可忽略三角形元素的贡献.最小代表单元可进一步简化为只由三根 “Z”型梁相互连结而成(图4(c)),并且标注为红色的部分(对应于三角形单元体)假定为刚体,不对应变能做贡献.另外,如图4(c)所示的等效最小代表单元的各梁段为连续梁,刚体和变形体连接处满足挠度和转角连续性条件.

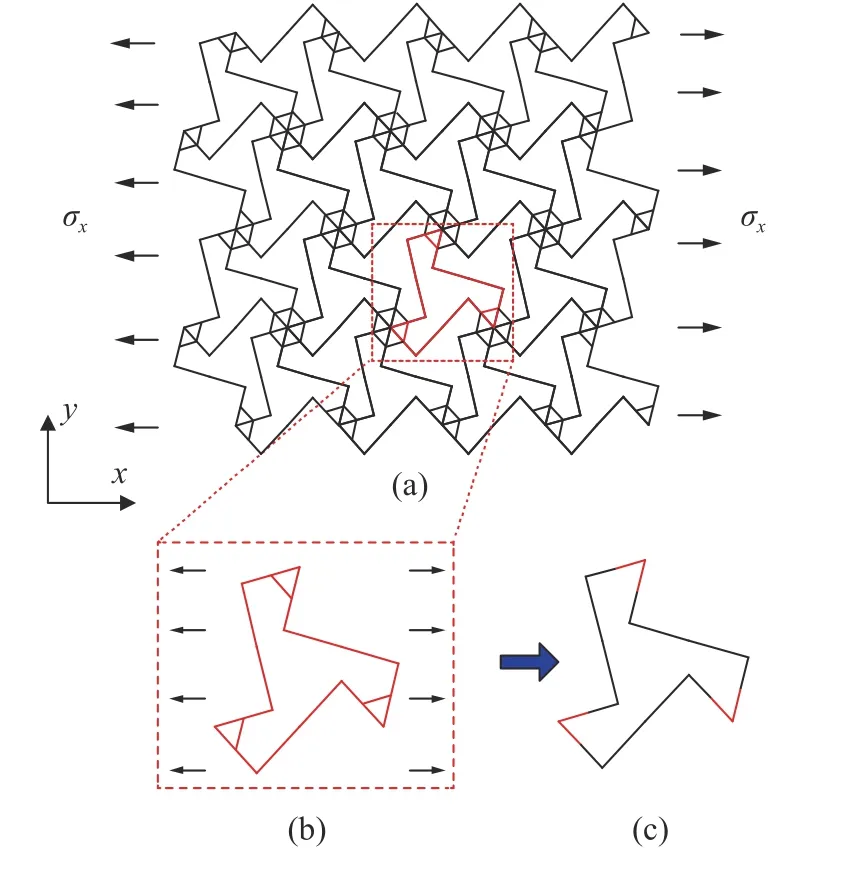
图4 (a) 阵列结构受远程应力示意图;(b) 最小代表单元受力图;(c) 等效最小代表单元Fig.4 (a) Schematic diagram of an enhanced hexa-missing rib lattice under far field uniaxial loading.(b) The related free boundary diagram of the smallest repeated unit.(c) The effective smallest repeated unit

2.1 任意形状的欧拉-伯努利梁力学模型

要确定最小代表单元的整体受力和变形条件,首要分析其“Z”形梁组件的力-位移关系.图4(c)所示的“Z”形梁变形时,可简化为一端固定铰接并作用有集中力偶MA,另一端滑动铰接,并作用有集中力偶MB和水平集中力N0的简支梁(如图5(a) 所示).去掉支座,代之以力,其对应的受力情况如图5(b)所示.由图5(b)易知

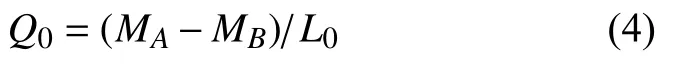
为了更具有普适性,“Z”形梁上任一截面(以轴线长度s标记,如图5(c)所示)的坐标可构造为轴线长度s的函数,即

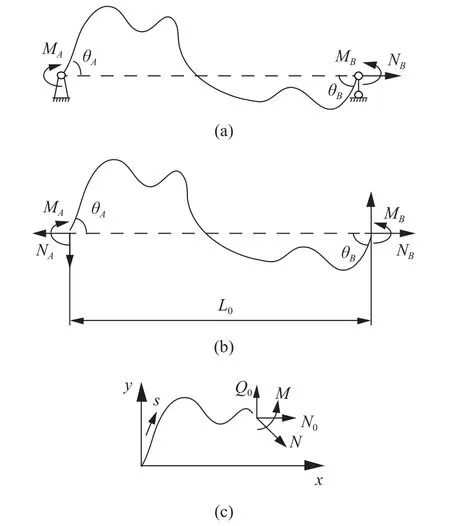
图5 任意欧拉-伯努利梁结构受力图Fig.5 Force diagram of an Euler-Bernoulli beam with arbitrary shape

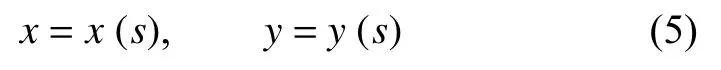
则截面s上的轴力N和弯矩M与x和y方向上的内力N0和Q0有关,分别为

其中,ES为基体材料的弹性模量;ES A=ES t和ES I=ES t3/12分别为单位厚度梁的拉伸刚度和弯曲刚度.

联合式(2)～式(5),可得

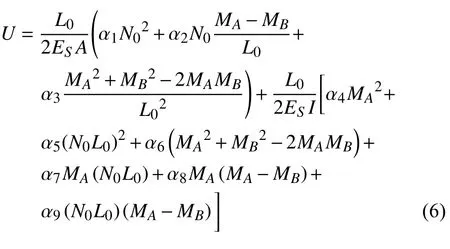
式中,αi(i=1,2,···,9) 为一组只取决于结构形状的无量纲参数,表达式为

运用卡氏定理,可以得出梁滑动端的位移(记为u,沿x方向)及两端旋转角 ωA和 ωB的表达式为

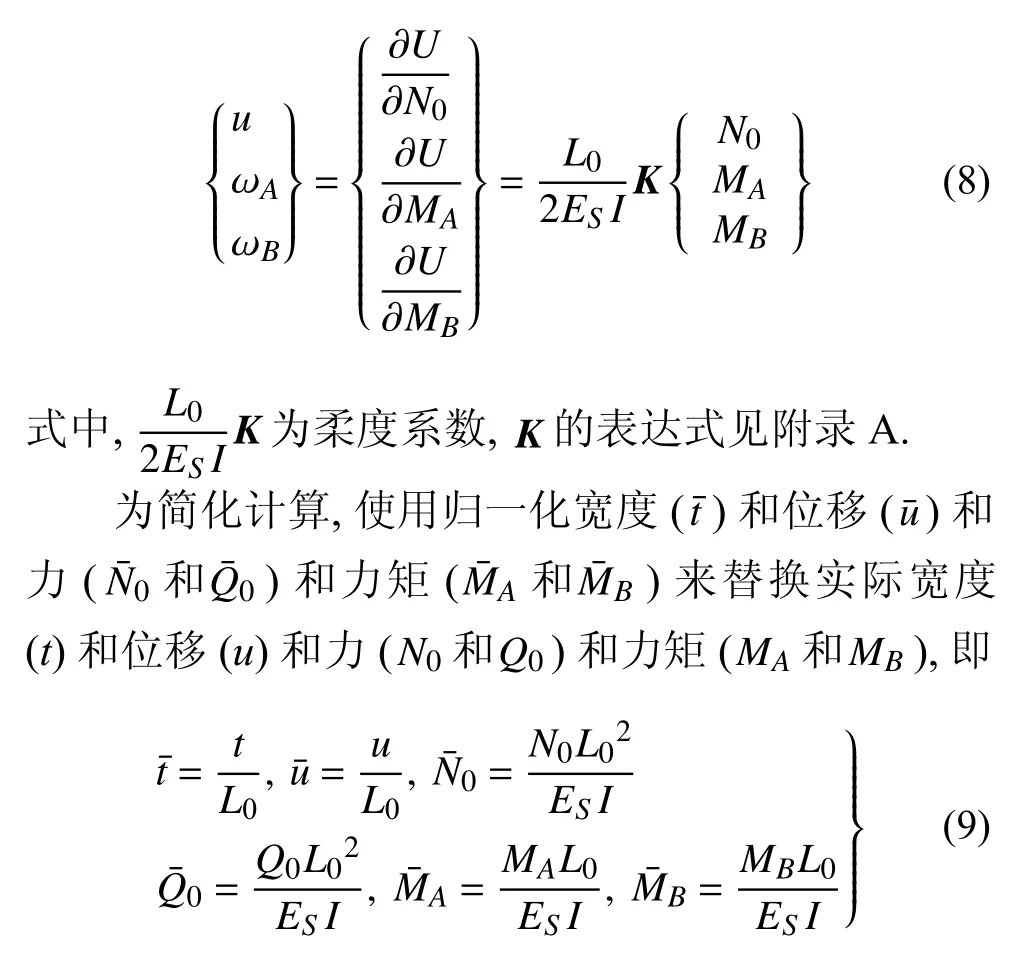
对式(8) 取逆,并代入式(9) 所示的归一化关系,可得

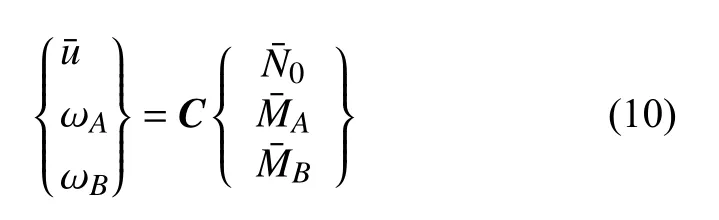
其中,C为柔度矩阵,表达式见附录A.其逆形式为

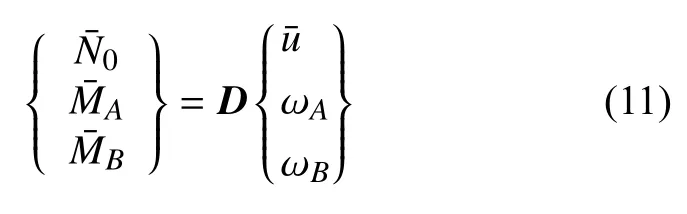
其中,D=C-1为刚度矩阵.

2.2 增强六手臂缺失支柱拉胀材料力学模型

如前所述,增强六手臂缺失支柱拉胀材料的最小代表单元可简化为如图4(c)所示的结构.打开三根“Z”形梁之间的连结,受力情况如图6 所示.

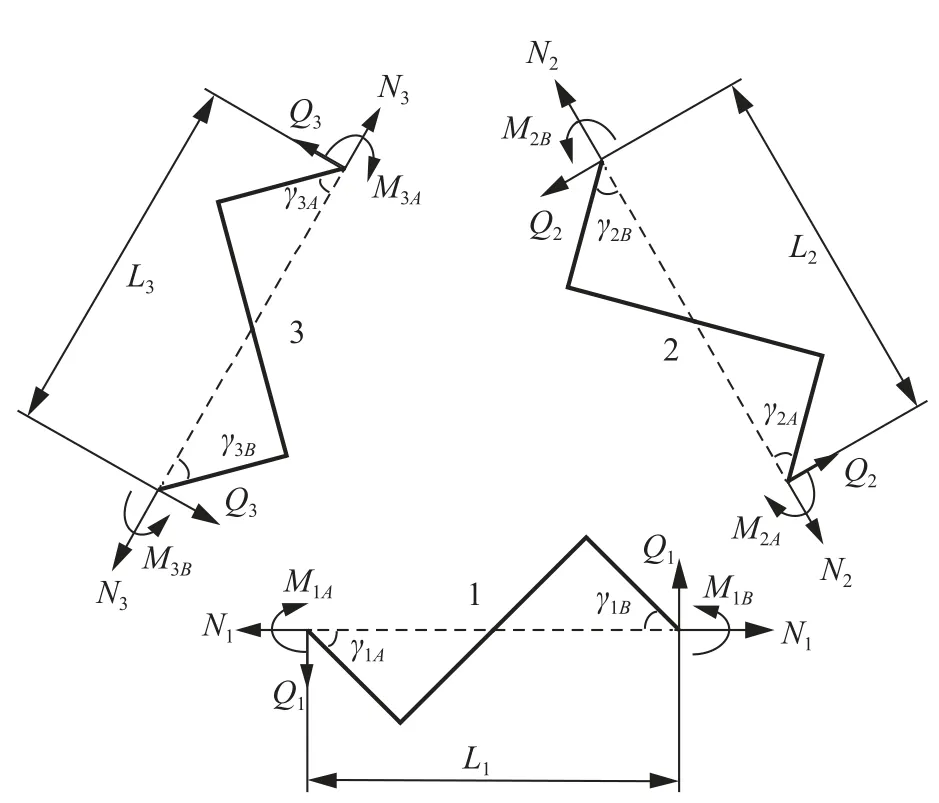
图6 最小代表单元各“Z”型梁受力图Fig.6 Force diagram of the zigzag ligaments of the smallest repeated unit

为描述方便,按照逆时针将“Z”形梁分别命名为1,2,3,并令Ni,Mi,Qi(i=1,2,3)表示结构的轴力、弯矩和剪力.

联立式(2)和式(9)可得

进一步根据梁2,3 连结处及梁1,2 连结处的受力平衡,可得

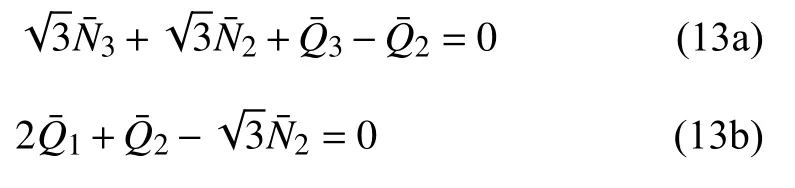
再考虑图4(b)所示的受力情况,根据水平方向受力平衡,可得

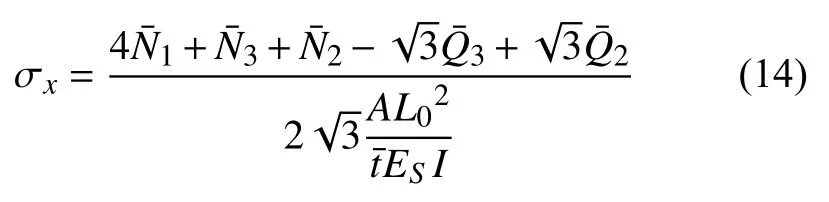
如前所述,每个元胞包含六个最小代表单元(图3(a)).

取元胞中心点附近的微小分离体,其受力情况如图7所示.根据力矩平衡条件,可得

血管环指主动脉弓及其分支血管的先天发育异常，由于胚胎时期多对鳃弓及成对的背侧主动脉未能顺序融合和吸收，在解剖上形成完全性或不完全性血管环，围绕气管和（或）食管造成压迫的一组先天性血管畸形，占先天性心脏病的1%～2%。每类血管环的预后存在显著差异，是否早期正确诊断和及时手术治疗是新生儿能否存活的关键。本研究是经过三血管序列切面对主动脉弓、动脉导管弓和气管三者关系的快速筛查，发现异常，再经弓降部管状切面进行验证，通过分析常见的血管环的胎儿超声心动图不同切面的特点，提高血管环的发现率及准确率。

图7 元胞中心节点区受力图Fig.7 Force diagram of an area surrounding the central point of the unit-cell

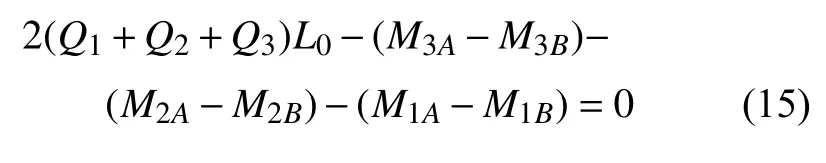
将式(12)代入式(15),进一步可得

本文仅考虑线弹性小变形情况,则最小代表单元三个“Z”形梁组件的三个连结点形成的图形在变形前后适中保持为封闭的三角形(如图8 所示).根据几何条件和变形相容条件,可得

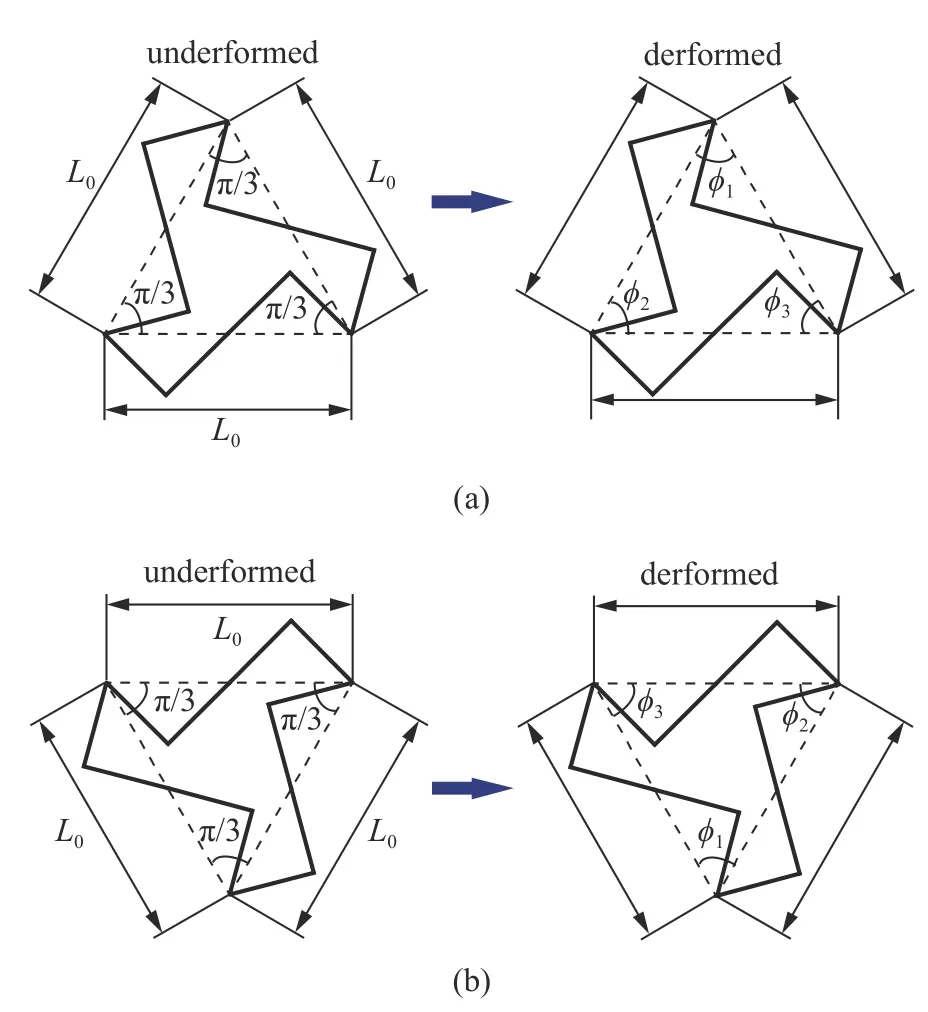
图8 最小代表单元变形示意图Fig.8 Schematic diagram of the deformation of smallest repeated unit

其中,θA,θB为杆件变形前两端切线与x轴的夹角(见图5); γiA,γiB为变形后夹角; φ1,φ2和 φ3为三角形变形后内角,L1,L2和L3为变形后梁1,2 和3 端点之间的直线长度.

由式(17b)进一步可得

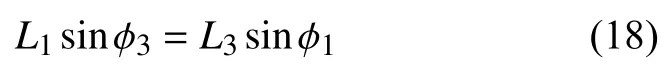
两边取微分,有

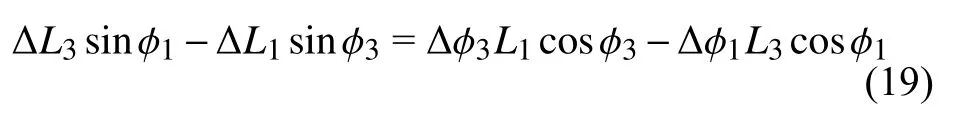
其中

小变形时可认为

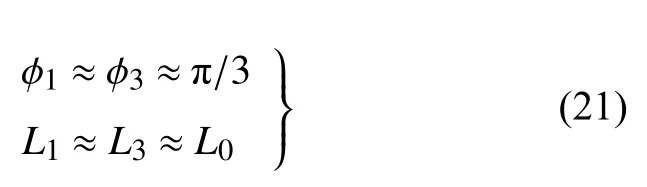
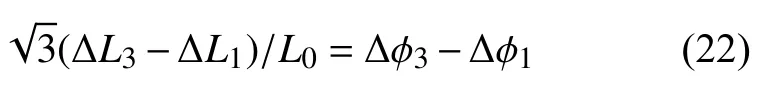
联立式(17a)、式(20)和式(21)可得

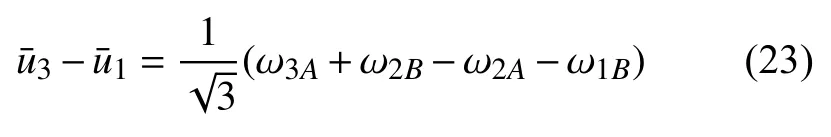
式中

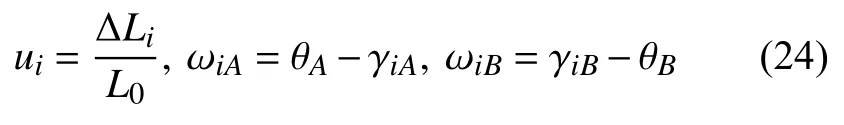
同理可得

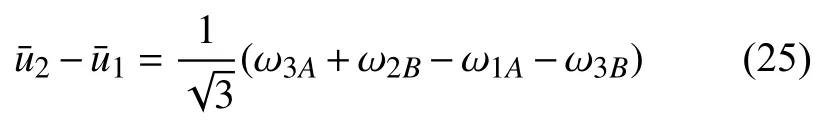
考虑最小代表单元的镜像结构(如图8(b)所示),易知

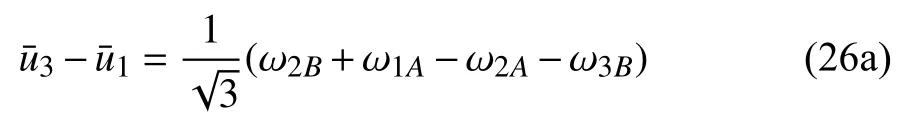
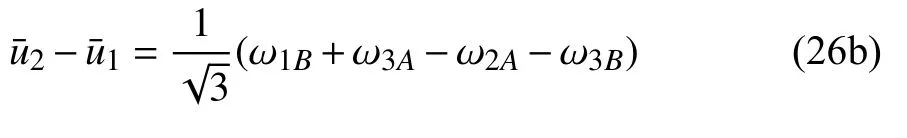
联立式(17a)和式(24)可知

图8(a)所示的最小代表单元在水平方向和竖直方向变形前后的长度分别为

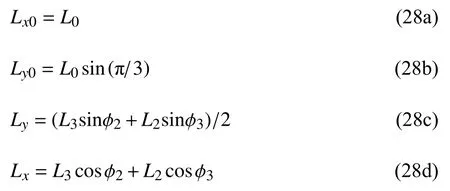
变形后的协调条件为,梁“2”和“3”在水平方向的投影长度之和与梁“1”的长度相等,即

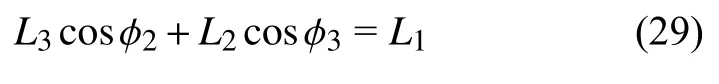
对式(28c)、式(28d)和式(29)微分可得

由式(30b)和式(31)可知

则最小代表单元的水平平均应变为

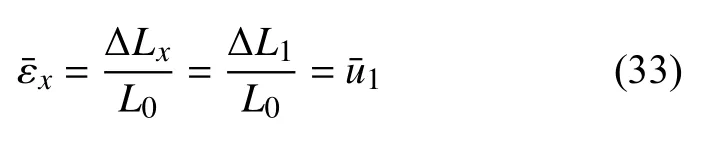
联立式(21)、式(24)和式(30a)可得

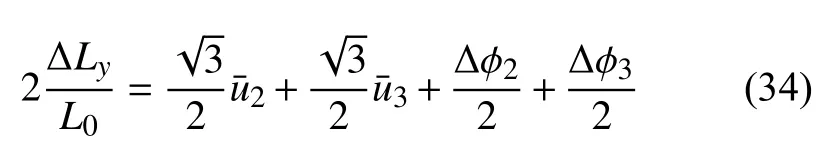
联立式(17a)、式(20)及式(27)可知

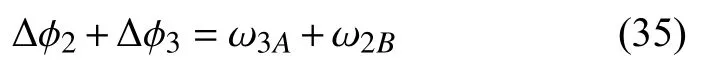
进一步联立式(26)、式(27)、式(34)和式(35)可知

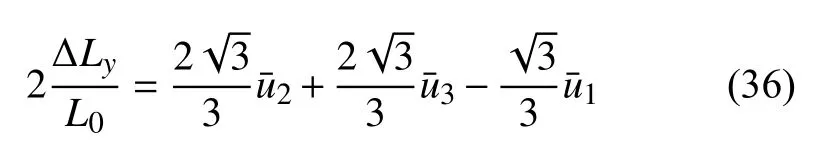
则最小代表单元的竖直平均应变可进一步表示为

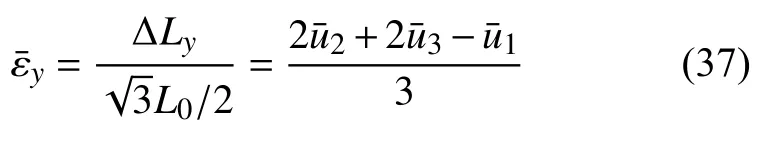
材料的等效弹性模量(以基体材料弹性模量进行归一化)和泊松比分别为

借助Maple 软件,联立方程式(11)～式(14)、式(17)、式(23)、式(25)～式(27)、式(33)及式(37)～式(39)可得等效弹性模量和泊松比分别为

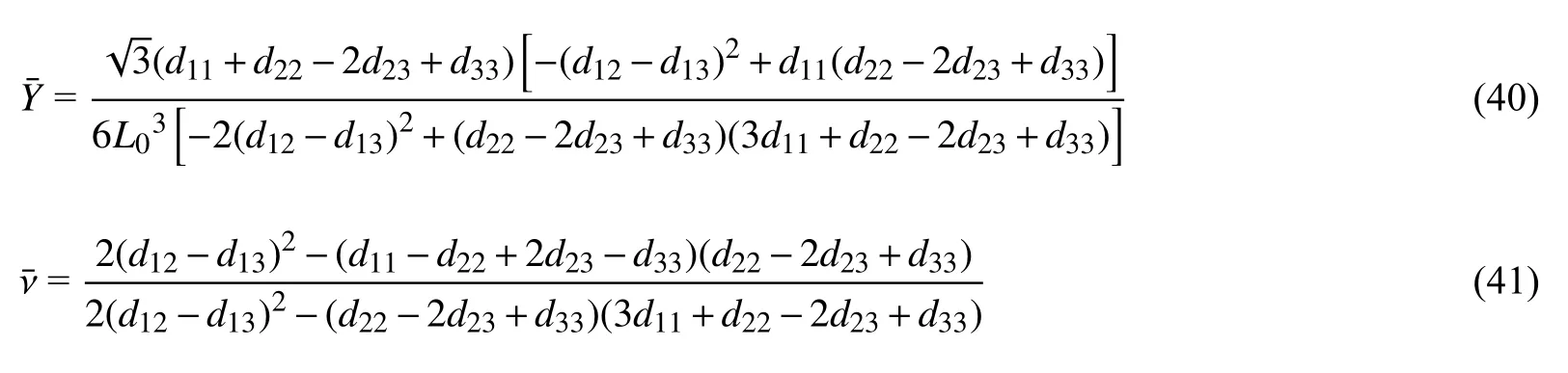
针对特定的结构形式,给出“Z”形梁的曲线描述方程,进一步给出式(7)中无量纲参数的具体形式,并带入式(40)和式(41)进行化简,即可得材料最终的等效弹性模量和泊松比的理论表达式.

需要指出的是,本节所描述的六手臂缺失支柱型手性拉胀材料等效力学参数的理论推导过程与Liu 等[43]的思路一致.但他们的工作中对如何利用平衡条件得到方程式(12)～式(14),及利用变形协调条件得到方程式(33)和式(37)阐述并不清晰.本文详细地陈述了这两个推导过程,增加了文章的可读性.

增强六手臂缺失支柱手性拉胀材料和增强六手臂(曲臂)缺失支柱手性拉胀材料的代表性“Z”形梁的计算模型如图9 所示.两种材料的曲线描述方程可见附录A.

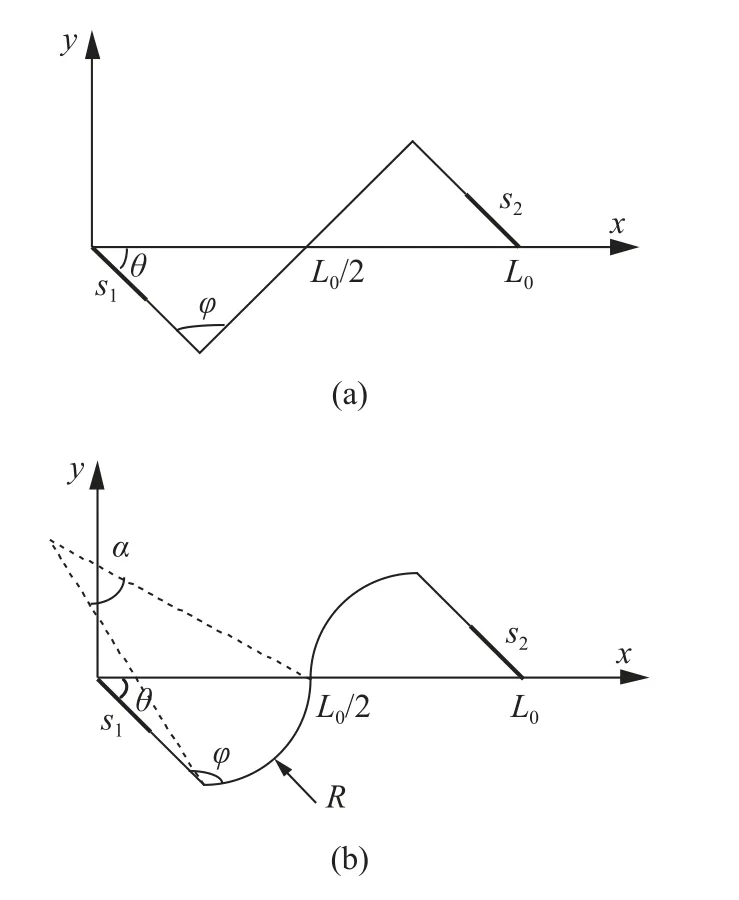
图9 (a) 直臂与 (b) 曲臂结构计算模型Fig.9 Calculation diagram of the enhanced hexa-missing rib auxetic honeycombs with (a) straight ligament and (b) wavy ligament

需要指出的是,通常情况下两种结构弹性模量和泊松比的理论表达式为包含上千项的多项式,无法继续化简.但根据理论推导,作者已经基于MATLAB 软件创建了图形用户界面(GUI),界面如图10 所示.对于直臂结构,只需输入内手臂长度r,外手臂长度L,增强率p,内角φ,手臂宽度t五个独立参数即可获得特定微结构形式的等效弹性模量和泊松比.对于曲臂结构,还需输入外手臂的半径R.

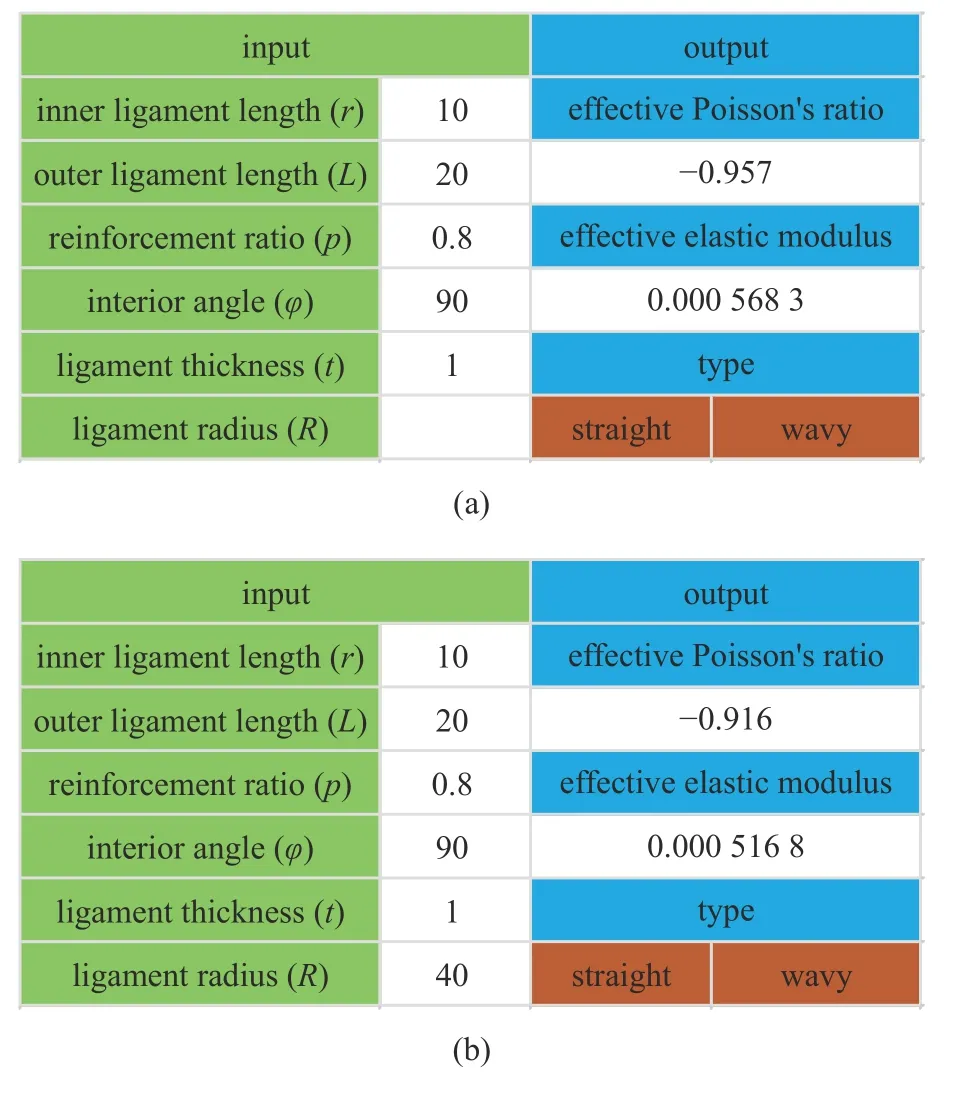
图10 图形用户界面: (a) 直臂结构计算和(b) 曲臂结构计算Fig.10 Graphical user interface: (a) calculation of auxetics with straight ligaments and (b) calculation of auxetics with wavy ligaments

另外,研究还发现,在L=2r这种特定的情况下,直臂结构的等效弹性模量和泊松比具有简洁的理论表达式,即

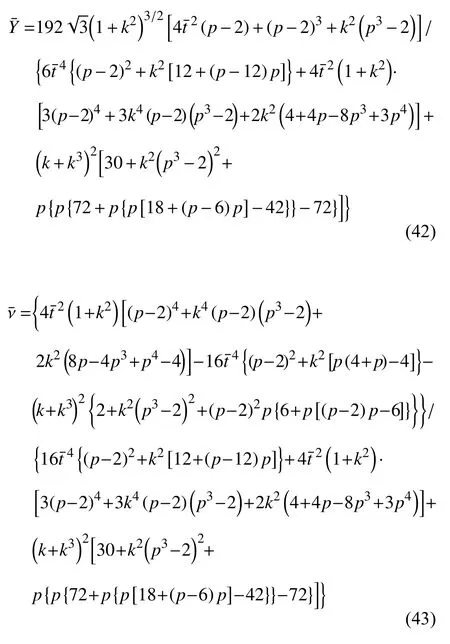
其中k=tanθ .

3 等效力学参数理论解讨论及有限元结果对比

本节将系统讨论直臂结构的等效弹性模量和泊松比与几何参数之间的关系,并将相应结果与有限元模拟进行对比.

为简化分析,本节所讨论的拉胀材料的手臂长度和手臂宽度之间的比例关系均固定为L:t=20.另外,作者的前期研究表明: 几何参数相同时,曲臂缺失支柱拉胀材料的负泊松比响应与直臂材料接近(图10 也可以证明),仅在增加保持恒定负泊松比的应变范围方面更有优势.因此,本节将仅讨论直臂结构.

3.1 力学参数云图

为了直观地研究几何参数对增强六手臂缺失支柱手性拉胀材料宏观力学性能的影响,图11 和12 分别给出了等效泊松比和弹性模量随手臂和中心绑扎桁架夹角 φ,增强率p及手臂比q变化的云图.

由图11 和图12 可见,改进的拉胀结构可以提供在大范围可调的泊松比(-1 到0)和弹性模量.由图11(a)可知: (1)结构的拉胀效应随着“Z”型手臂内角的增大而减弱,这是由于内角的增大意味着长手臂和中心绑扎桁架的连结处刚度减弱,抑制了中心绑扎桁架的旋转效应;(2)由于中心绑扎桁架的刚性随增强率的增加而增强,结构的拉胀效应随着增强率的增大而增强.但由图8(b)可知,拉胀效应与手臂比的关系是非单调的,表现出两个阶段的演变,在第一阶段(q达到阈值之前,图11(b)中黑色线表示),手臂比越大拉胀效应越强,第二阶段则相反.这是因为q越大意味着外手臂相对中心绑扎桁架越强,因而更容易触发结构的旋转效应,具有更好的拉胀效应.但q持续增大时,结构逐渐趋于三角形网络结构,不具有拉胀特性.因此,结构的泊松比演化和q的关系表现出了两阶段的特征.

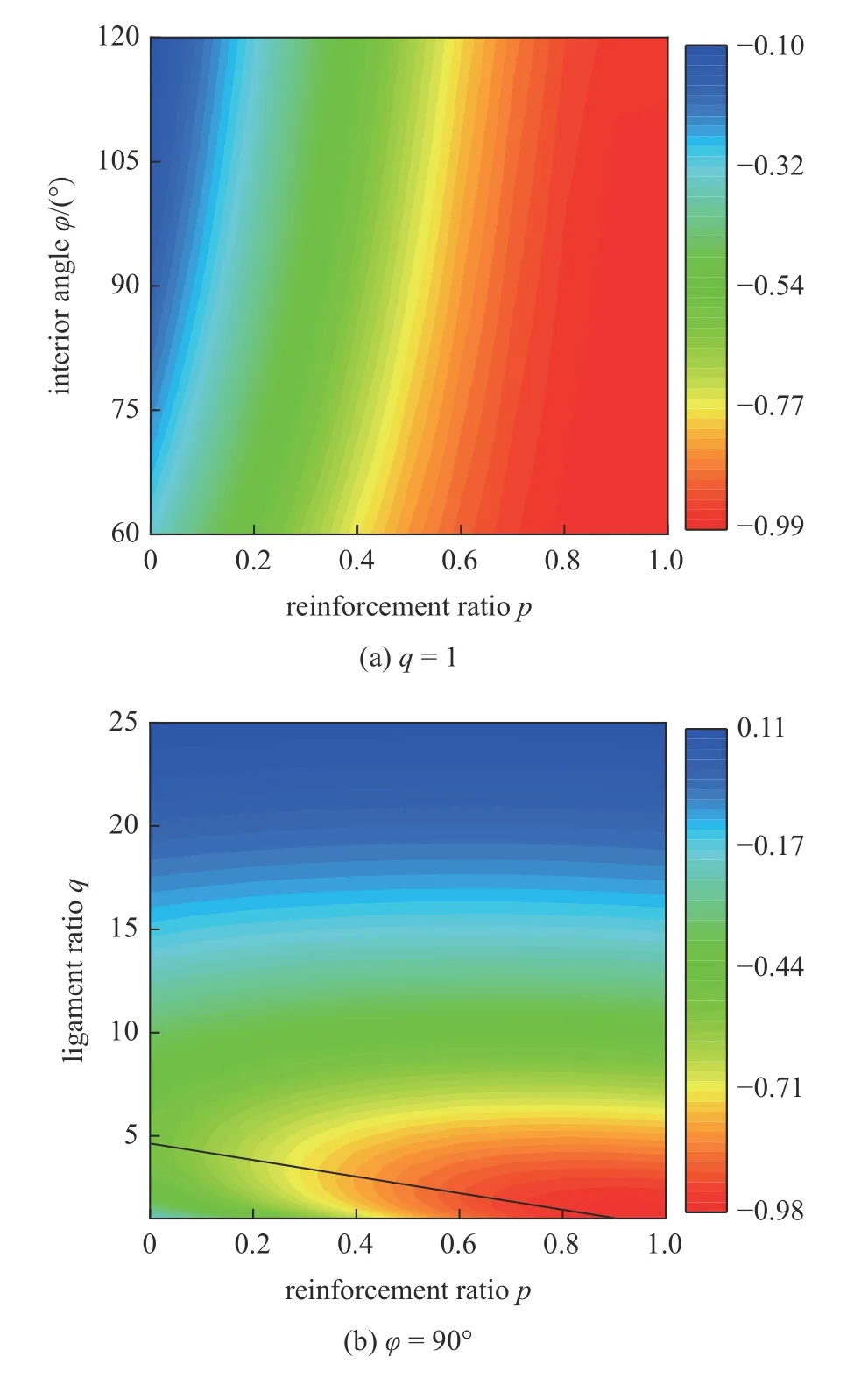
图11 结构等效泊松比云图Fig.11 Contour plots the effective Poisson’s ratio over a wide range

由图12 可知,结构的弹性模量随着夹角、增强率和手臂比的增大而单调增大.

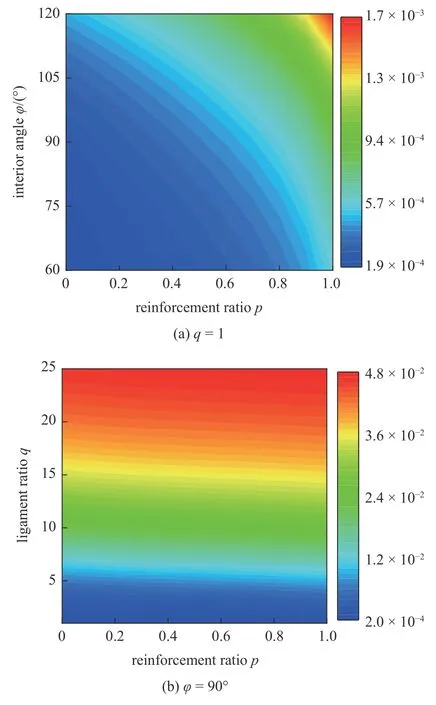
图12 结构等效弹性模量云图Fig.12 Contour plots the effective elastic modulus over a wide range

3.2 有限元结果对比

本节进一步将等效泊松比和弹性模量的理论解析结果与有限元计算结果进行了比较.

有限元计算采用ABAQUS 软件完成.计算时设定如下: (1)基体材料弹性模量和泊松比分别为1 和0.3;(2) 单元类型为CPE4 四节点平面应变单元;(3)根据网格收敛性分析,网格尺寸为0.25t,即: 保证沿梁厚度方向至少有4 个单元;(4)由于第2 章的理论推导是在线弹性小变形下开展的,本节的有限元计算也局限为线弹性小变形分析;(5)计算针对单一元胞结构展开,为消除边界条件的影响,对元胞结构施加了周期性边界条件(详见附录B).

图13 给出了变形较大时(等效应变为5%)不同几何参数最小代表单元的最大面内主应变云图.由图可见,结构整体变形较大时,各部件的局部变形相对很小,验证了假定(4)的合理性.另外,图13 还表明,结构的三角形元素部分的应变很小,也说明了理论推导时将其假定为刚体部件的合理性.

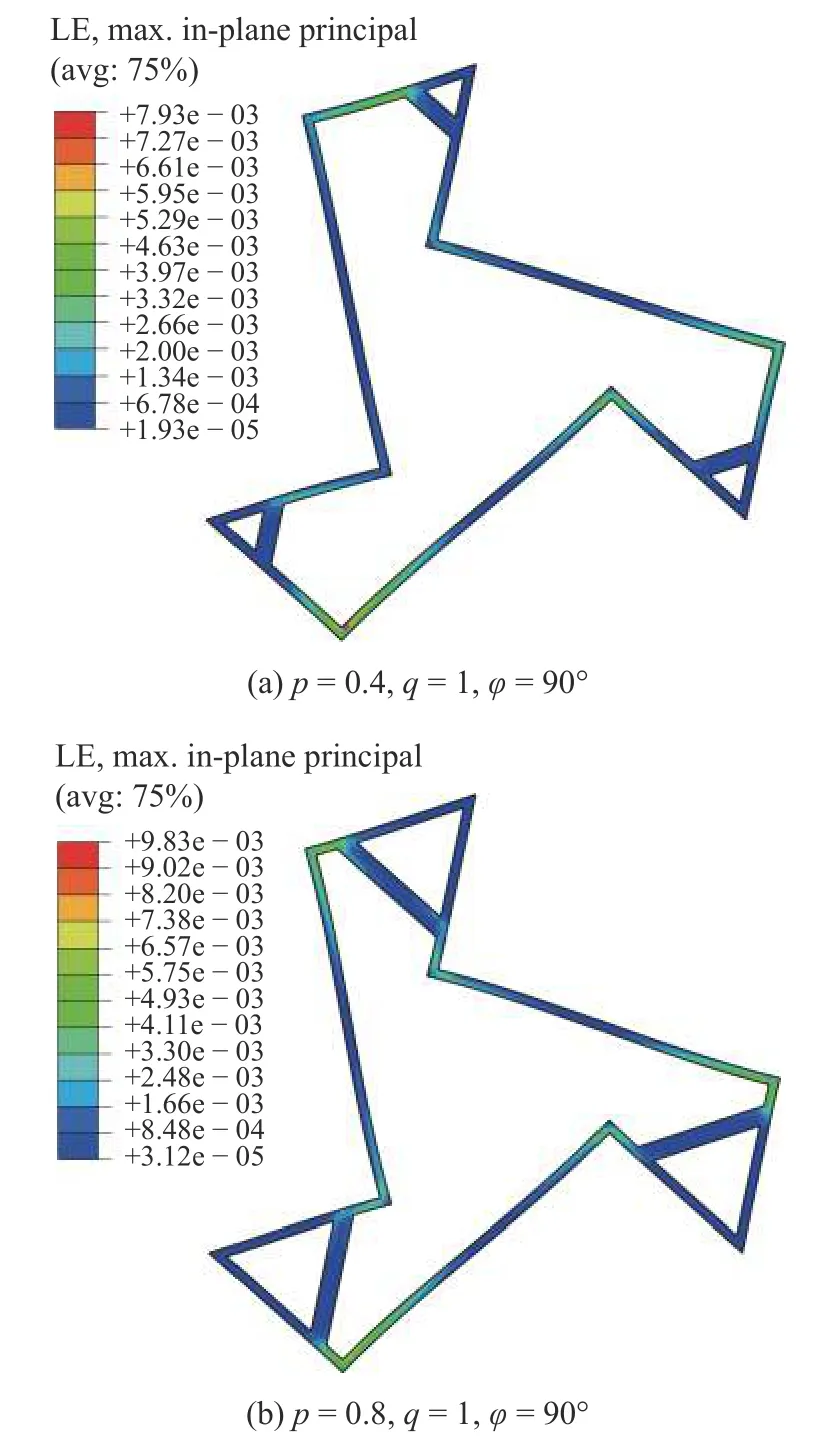
图13 等效应变为5%时最小代表单元最大面内主应变云图Fig.13 Contour plots the maximum in-plane principal strain of the smallest repeated units at an effective strain of 5%

图14 和图15 为不同几何尺寸下,结构等效泊松比和弹性模量的理论值与有限元结果.显然,两种结果吻合的较好.

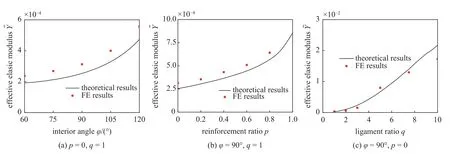
图15 不同几何参数下结构等效弹性模量的理论和有限元模拟结果对比图Fig.15 Theoretical and FE results of the effective elastic modulus of the enhanced hexa-missing rib auxetic honeycomb over a range

需要指出的是,本文的理论解是基于将最小代表单元的三角形部分假定为刚体这一假设而推导的.在结构受载时,三角形部分不可避免地也会产生变形(并且其变形的程度受结构相对尺寸的影响),这部分变形同样也会对结构总变形能做贡献.另外,理论解中将实体结构简化为梁,所有与长度相关的尺寸均为各梁段中性轴的长度.但事实上实体结构的结果与梁的结果也会有偏差.理论模型的精度及误差主要源自上述两个因素,并且这两个因素对理论值的影响并不同向,会存在竞争关系.因此,图14和15 中部分理论结果比有限元结果大,而另一部分比有限元结果小.

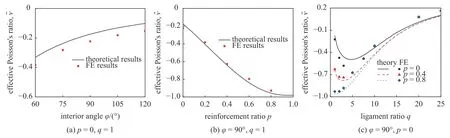
图14 不同几何参数下结构等效泊松比的理论和有限元模拟结果对比图Fig.14 Theoretical and FE results of the effective Poisson’s ratio of the enhanced hexa-missing rib auxetic honeycomb over a range

4 结论

基于能量法,本文首先在小变形框架下推导了前期研究工作中发展的增强六手臂缺失支柱手性拉胀超材料的等效力学性能参数的理论模型.研究表明,只有在微结构具有特定几何参数时,增强六手臂缺失支柱手性拉胀超材料的等效泊松比和弹性模量才有简洁的理论表达式.因此,为便于理论模型的应用,本文进而开发了MATLAB 图形用户界面,只需输入几何参数就可以方便地直接获取相应结构的等效力学性能参数.最后,系统讨论了关键几何参数对结果力学性能的影响规律.

需要指出的是,本文的研究局限于理论推导和有限元分析.在后续的工作中,作者拟开展系统的实验研究来考察增强六手臂缺失支柱手性拉胀超材料的静/动态力学性能.

附录A

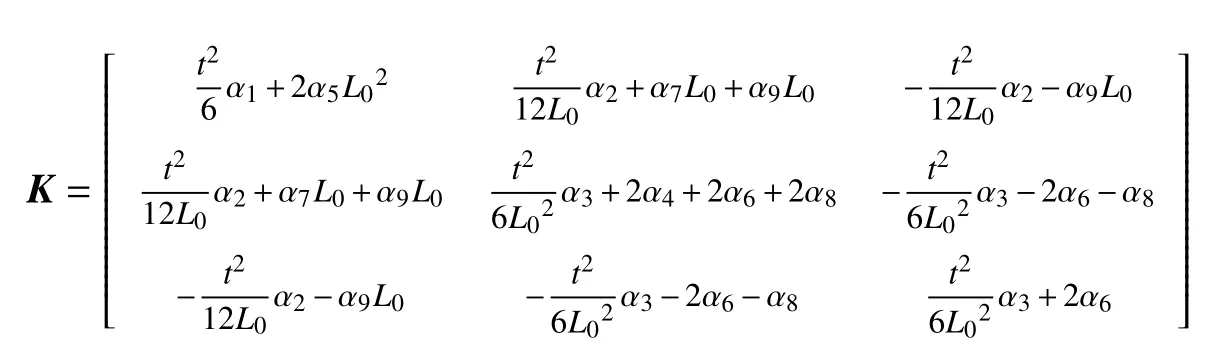
其中

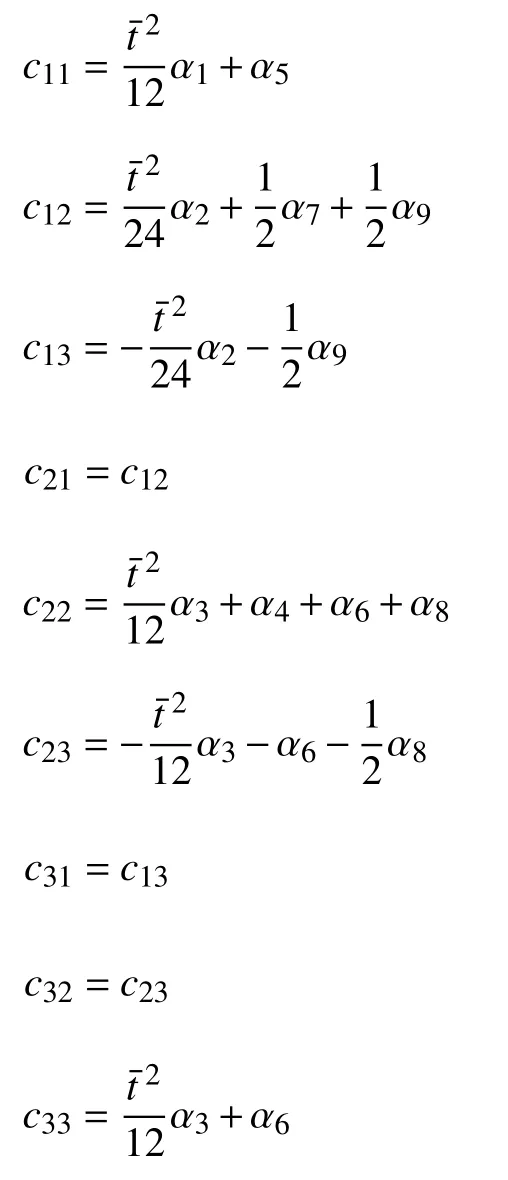
直臂结构曲线描述方程

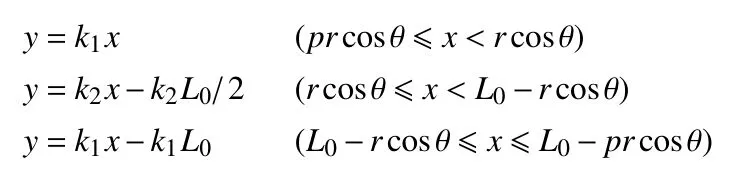
曲臂结构曲线描述方程

附录B

为简化计算,本文的分析只针对单一元胞结构,采用基于ABAQUS 软件的有限元均匀化方法来考察手性拉胀材料的等效力学行为.为消除边界条件的影响,计算时对元胞结构施加了周期性边界条件[52-53],即

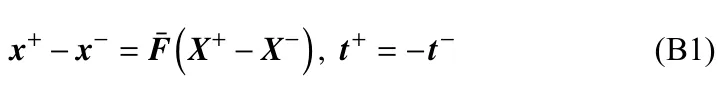
式中,x±和X±分别为对应边界的空间和参考坐标;t±=P±N±代表外法向为N±边界上节点的牵拉应力(P为第一类皮奥拉-基尔霍夫(Piola-Kirchhoff)应力).等效变形梯度F¯ 及等效第一类皮奥拉-基尔霍夫应力可表示为

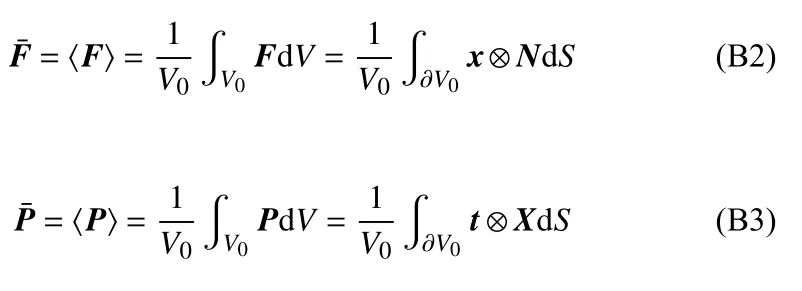
式(B2)和式(B3)中,V0和 ∂V0分别为元胞在参考坐标系下的体积和边界.

元胞的整体变形可由等效Biot 应变[54]来度量,即

其中,1 为二阶单位张量.

等效泊松比可定义为

图B1 给出了特定结构尺寸下(p=0.6,q=1,φ=90°)对一个单胞施加周期性边界条件以及对阵列结构(含n×n个单胞)直接建模所得的等效泊松比结果的对比.由图可见,随着n(n为阵列结构中完整单胞的数目)的增加,阵列结构直接建模的计算结果将收敛于周期性边界条件获得的结果,验证了周期性边界条件结果的准确性.

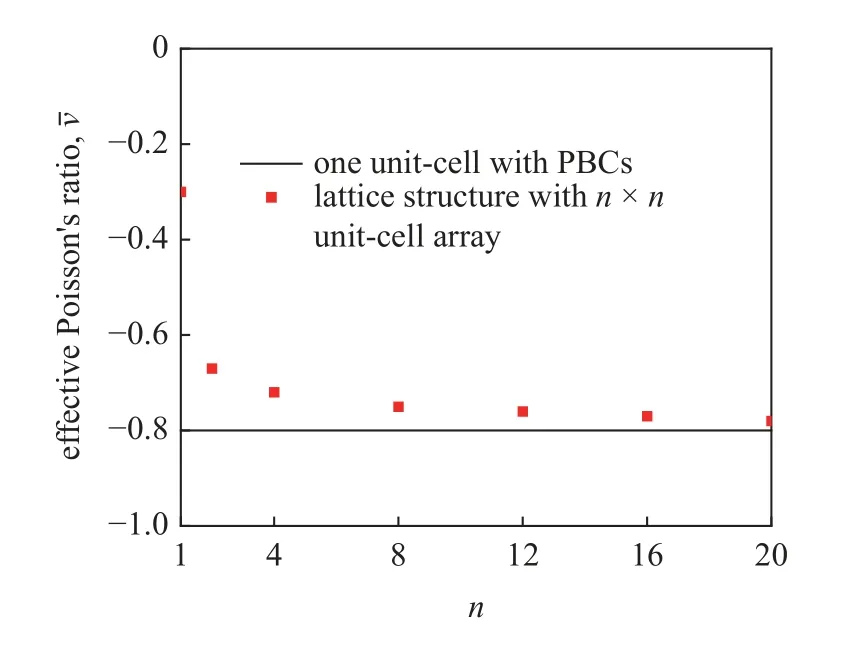
图B1 对一个单胞施加周期性边界条件以及对阵列结构(包含n× n单胞)直接建模所得泊松比对比图 (p =0.6,q=1,φ=90°)Fig.B1 The effective Poisson’s ratio obtained by the PBCs-based homogenization method and calculated from lattice structures consisting of n× nunit-cell array (p =0.6,q=1,φ=90°)