金字塔点阵圆筒结构轴向弹性波传递特性研究1)

2022-11-06刘海东张满弓

力学学报 2022年10期

关键词：环向圆筒杆件

任怡张昊张望刘海东李钊张满弓,2)

* (西南科技大学制造过程测试技术教育部重点实验室,四川绵阳 621010)

† (武汉第二船舶设计研究所,武汉 430064)

** (天津航天瑞莱科技有限公司,天津 300462)

引言

点阵结构一般是由连续、重复排列的相互连通的单元组成的三维结构,也可以理解为三维空间中由相互连通的支柱和节点组成的多孔材料结构[1-3].点阵结构的周期和多孔特征使其具有特殊的力学和声学特性,如比强度高、比刚度大、轻质和隔振等,在航空航天、舰船等领域具有十分广泛的应用前景[4-8].

对点阵结构的减振和隔声性能,已经有广泛的理论[9-10]和实验研究[11-13],点阵结构通过单胞的周期性排列获得声子晶体带隙,在带隙范围内抑制弹性波的传播[14-16].An 等[17]提出了一种基于拉伸主导的三维声学超材料点阵结构,通过振动传递试验验证了其结构的减振性能.Liu 等[18]将一些辅助结构引入点阵结构,使用布洛赫定理和有限元相结合的方法研究了弹性波在这种改进的二维点阵结构中的传播,通过对辅助结构的参数分析,设计了一种基于改进点阵结构的宽频带隔振结构.Matlack 等[19]将局域共振结构和点阵结构相结合,提出了一种弹性超结构,可以实现低频宽带隙的减振效果.Cao 等[20]通过有限元方法和实验研究了杆件截面变化的点阵结构,讨论了形状参数对点阵结构的力学性能和能量吸收能力的影响,并得到了最优的杆件形状参数.文献[21]在立方体点阵结构上附加了局部谐振器,研究了不同尺寸和质量的局部谐振器对带隙的宽度和位置的影响.Wu 等[22-23]使用谱元法研究了由两种不同材料组成的晶格结构的振动带隙特性,参数分析了结构和材料对带隙的影响.Syam 等[24]设计了六种不同的点阵结构,并使用有限元方法和实验研究了这些结构的减振性能.Wang 等[25]使用遗传算法在最小重量的前提下对夹层板的声学和力学性能进行了优化设计研究,最终得到了一种重量轻、机械效率高的隔音材料.

与目前广泛研究的基于二维平面和三维长方体的点阵结构不同,点阵圆筒结构是沿轴向和环向周期性阵列的结构.对点阵圆筒结构的研究主要集中于结构的力学性能[26-28],而缺乏对其低频宽带减振的相关研究.事实上,针对圆筒结构(如管道)等,存在着丰富而又迫切的应用场景,如化工管道和舰船管道的低频减振降噪控制等,合理的骨架结构形式将是能否实现预期隔振效果的关键.因此,本文以金字塔型单胞为对象,通过环向和轴向阵列形成点阵圆筒结构,针对独立参数进行结构设计,并联合ABAQUS 对结构轴向减振性能进行分析.利用无量纲参数系统分析了金字塔单胞的高和宽,杆件的直径以及环向阵列的个数对金字塔点阵圆筒结构轴向减振性能的影响规律.在此基础上,设计了一种具有低频宽带减振性能的金字塔点阵圆筒结构,利用3D打印技术制备了样件,完成振动实验测试并与有限元模拟结果进行对比.

1 金字塔点阵圆筒结构参数化模型

通过Rhino 和Grasshopper 等软件建立的金字塔点阵圆筒模型如图1 所示,主要结构参数如下: 金字塔单胞轴向和环向阵列的个数分别为m和n,结构的内接圆和外接圆的半径分别为rc和Rc,金字塔单胞的四根杆件的交点为底面四边形的中心,为等腰四棱锥结构,杆件为圆柱杆,直径为d,单胞的长宽高分别为a,b和h,一共有8 个结构参数,它们之间满足如下关系

图1 金字塔点阵圆筒结构示意图Fig.1 Schematic diagram of the pyramid lattice cylinder structure

所以独立的结构参数只有6 个.

Rhino 是目前普遍应用的三维NURBS 工业建模软件,Grasshopper 是与Rhino 紧密结合的参数化设计插件.Grasshopper 作为一种节点可视化编程语言,是一种图示算法编辑器或者可视化脚本编辑器,可高效实现实时数据结构调整并观察、记录结构的推敲过程[29].因此,本文使用Rhino 和Grasshopper软件对结构进行建模,固定选取金字塔点阵圆筒结构的内接圆半径rc=100 mm,通过改变杆件的直径、金字塔单胞的宽和高、单胞环向和轴向阵列的个数,实现对金字塔点阵圆筒结构的设计和模型生成.

2 结构轴向振动有限元模型

本研究关注金字塔点阵圆筒结构轴向振动的控制情况,为了验证结构的减振性能,利用有限元仿真分析结构的振动传输特性,通过在一定频率范围内进行谐响应分析得到响应曲线,从曲线中可以直观获得结构对弹性波的衰减能力.传输特性函数(FRF)的定义为

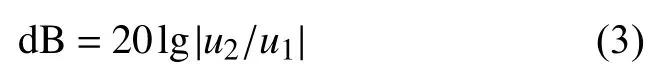
式中,u1和u2为振动传输激励和响应的位移值.

利用有限元软件ABAQUS 进行模拟仿真[30],在金字塔点阵圆筒结构的左端面施加z方向的位移激励,并在右端面提取位移响应,有限元模型如图2 所示,选用梁单元.计算中使用的具体结构参数如表1所示,使用的材料为树脂,密度ρ=1180 kg/m3,弹性模量E=2 GPa .图3 给出了两个模型(轴向阵列个数不同)在轴向位移激励下的振动传输特性曲线.从图中可以看出,在116～466 Hz 范围内,两个模型的轴向振动都有较大衰减,且随着轴向阵列个数的增加,振动衰减的强度逐渐增大.

图2 有限元模型Fig.2 Finite element analysis model

表1 金字塔点阵圆筒模型结构参数Table 1 Structural parameters of pyramid lattice cylinder model

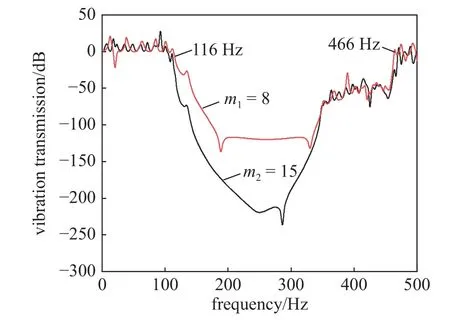
图3 振动传输特性曲线Fig.3 Vibration transmission characteristic curve

3 金字塔点阵圆筒结构参数影响分析

量纲分析理论表明,某一物理过程不因其中相关物理量量纲选择的任意性而改变,由此可以得到物理量之间的关系[31].因此,本文将引入归一化频率的概念,用于对频率进行无量纲处理.归一化频率定义为

式中,f,rc和分别为结构的频率、内接圆半径和纵波波速,根据归一化频率的表达式可以得知,归一化频率与具体材料选取和结构的内接圆半径无关.

同时为了评估结构振动衰减的能力,使用无量纲参数—相对带宽BG%的概念,其定义为

式中,fH和fL分别为带隙的上、下边界频率值,相对带宽即为带宽与中心频率之比[32-34].使用相对带宽的概念可以降低带隙效果评价对绝对频率的依赖,便于在更宽频率范围内统一评估结构的减振效果,一般认为BG%越大,减振效果越好.

学科地位的确定，不是学科建设的终结，而是学科建设的开始。治安学虽然学科地位得以确认，但它还只是正在成长中的新兴学科。审视治安学学科的形成与发展，不难发现学科成熟程度低，学科建设问题多的现状。

下面将利用无量纲参数—归一化频率和相对带宽,系统讨论金字塔点阵圆筒结构中单胞环向阵列的个数、单胞的宽和高以及杆件的直径对结构减振效果的影响.

3.1 单胞的宽对金字塔点阵圆筒结构振动传输特性的影响

金字塔单胞的宽决定了点阵结构的轴向长度,当选取单胞的高为28.4 mm,杆件直径为1 mm,轴向和环向阵列个数分别为15 和20,此时金字塔点阵圆筒结构的外接圆半径为130 mm.改变单胞的宽,得到不同单胞宽的金字塔点阵圆筒结构振动传输特性曲线如图4 所示,当单胞的宽为20.00 mm,33.33 mm和46.67 mm 时,带隙的起始归一化频率分别为:0.010,0.009 和0.008,终止归一化频率分别为: 0.047,0.040 和0.032.由此可见,随着单胞的宽增加,带隙向低频移动,带宽变小,相对带宽分别为129.82%,126.53%和120.00%.

图4 不同单胞宽下的振动传输特性曲线Fig.4 Vibration transmission characteristic curves of different unit cell widths

3.2 单胞的高对金字塔点阵圆筒结构振动传输特性的影响

选取单胞的宽为40 mm,杆件直径为1 mm,轴向和环向阵列个数分别为15 和20 时,改变单胞的高,分别取8.65 mm,18.52 mm 和28.40 mm,此时的金字塔点阵圆筒结构的外接圆半径分别为110 mm,120 mm 和130 mm.不同单胞高对金字塔点阵圆筒结构振动传输特性的影响如图5 所示,当单胞的宽为8.65 mm,18.52 mm 和28.40 mm 时,带隙的起始归一化频率分别为: 0.024,0.013 和0.009,终止归一化频率分别为: 0.062,0.045 和0.036.由此可见,随着单胞高度增加,带隙向低频移动,带宽变小,相对带宽分别为88.37%,110.34%和120.00%.

图5 不同单胞高下的振动传输特性曲线Fig.5 Vibration transmission characteristic curves of different unit cell heights

综合考虑金字塔单胞的高和宽对整个结构减振性能的影响,从图6 可以看出,随着金字塔单胞的高和宽的增加,带隙频率的上限和下限都在降低,带隙频率的上限比下限降低的幅度更大,所以结构的带隙往低频移动时,整个带隙的宽度也在变小.从相对带宽的角度去评价整个结构的低频宽带减振性能,如图6(d)所示,随着金字塔单胞宽的增加,相对带宽变小,随着单胞高度增加,相对带宽变大.相比于单胞宽的影响,相同的变化幅值下,单胞高对结构的减振性能影响更大,所以在考虑设计金字塔点阵圆筒结构用于振动控制时,应该主要考虑金字塔单胞高对结构减振性能的影响.

图6 单胞的高和宽对结构减振性能的影响Fig.6 The effect of unit cell height and width on structural vibration reduction performance

图6 单胞的高和宽对结构减振性能的影响(续)Fig.6 The effect of unit cell height and width on structural vibration reduction performance (continued)

3.3 单胞杆件的直径对金字塔点阵圆筒结构振动传输特性的影响

选取单胞的宽为40 mm,单胞的高为28.4 mm,轴向和环向阵列个数分别为15 和20 时,改变金字塔单胞杆件的直径,分别取0.5 mm,1.0 mm 和1.5 mm,得到图7 所示的传递特性曲线,当杆件的直径为0.5 mm,1.0 mm 和1.5 mm 时,带隙的起始归一化频率分别为: 0.004,0.009 和0.013,终止归一化频率分别为: 0.018,0.036 和0.054.由此可见,随着杆件的直径增加,带隙向高频移动,带宽变大,相对带宽分别为127.27%,120.00%和122.39%.杆件的直径直接影响整个结构的剪切刚度和等效密度,改变整个结构的减振性能,杆件越细,在低频时的减振效果越好,但是结构的刚度会随之变小,所以在结构设计中,应该首先满足结构刚度的需要,然后选择较小的杆件直径,以达到低频减振的效果.

图7 不同杆件直径的振动传输特性曲线Fig.7 Vibration transmission characteristic curves of different rod diameters

3.4 单胞环向阵列的个数对金字塔点阵圆筒结构振动传输特性的影响

选取单胞的高和宽分别为28.4 mm 和40 mm,杆件直径为1 mm,轴向阵列个数为15,此时金字塔点阵圆筒结构的外接圆半径为130 mm.改变单胞环向阵列的个数,得到不同单胞环向阵列个数下金字塔点阵圆筒结构振动传输特性曲线如图8 所示,当环向阵列的个数为10,20,30 和40 时,带隙的起始归一化频率分别为: 0.007,0.009,0.010 和0.010,终止归一化频率分别为: 0.027,0.038,0.041 和0.044.由此可见,随着环向阵列个数的增加,带隙向高频移动,带宽变大,相对带宽分别为121.89%,123.72%,120.93%和124.72%.从中发现,当环向阵列个数从30 增加到40 时,结构的带隙范围变化显著减小,对结构减振性能的影响减弱.

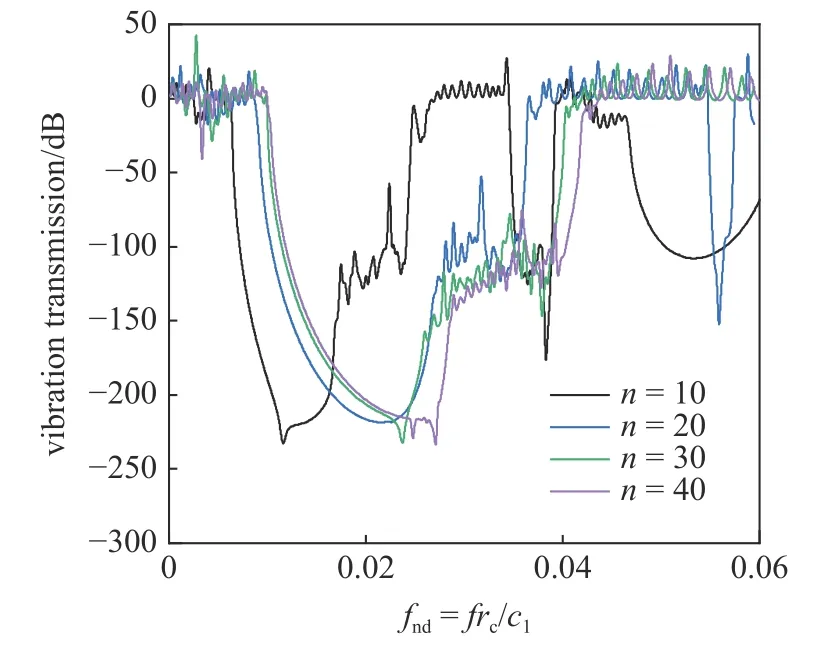
图8 不同单胞环向阵列个数下的圆筒振动传输特性曲线Fig.8 Vibration transmission characteristic curves of different numbers of unit cell circular arrays

3.5 等比例模型参数分析

本文重点关注的结构参数为单胞的高、宽和杆件的直径.为了进一步探究这些结构参数之间的关系,使单胞的高、宽和杆件的直径控制在一定的比例,如b:h:d=20.0:14.2:0.5,同时改变三个参数的数值,如表2 所示,此时固定金字塔单胞轴向、环向阵列的个数为15 和20,结构内接圆的半径为 100 mm.得到的振动传递曲线和相对带宽随着杆件直径变化的结果如图9 所示,当单胞的高、宽和杆件的直径三个参数的比值为上述定值时,随着杆件的直径增加,带隙向低频移动,带宽减小,但是结构的相对带宽BG%是一样的,均为122.50%左右.

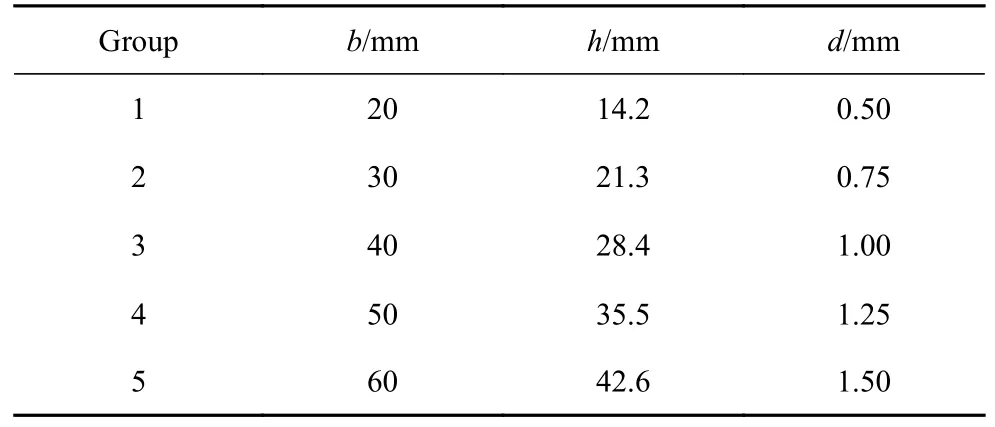
表2 等比例模型的结构参数Table 2 Structural parameters of the equal scale model

图9 等比例模型的带隙范围和相对带宽Fig.9 Band gap and relative bandwidth for the equal scale model

在实际应用中,当结构内接圆的半径为 100 mm时,为了保证结构整体的协调性和力学性能,单胞的高、宽应不大于60 mm,杆件的直径不大于5 mm,此时单胞的高、宽和杆件的直径的比值如果相同,带隙频率会随着结构参数有规律的变化.定义无量纲结构参数k为直径的变化量 Δ 与结构内接圆半径rc的比值,其表达式为k=Δ/rc.如图9 所示,以杆件直径为1 mm 的模型为基准,随着直径大小改变,无量纲结构参数k相应变化,其带隙范围变为[2-100k fL0,2-100k fH0],fL0和fH0分别为杆件直径为1 mm 时的带隙频率下限和上限.

点阵结构的固有频率决定了带隙宽度和频率位置,固有频率f0正比于结构刚度k0与质量m0比值的1/2 次方,即[24].结构的刚度越低,参与振动的质量越大,那么结构的固有频率就会越低,带隙范围的频率也就越低[35].图10 为等比例模型中随杆件直径变化的结果,其反映了结构固有频率的变化趋势,随着等比例模型中杆件直径的增加,结构固有频率减小,带隙向低频移动,与图9 中的结果相符合.

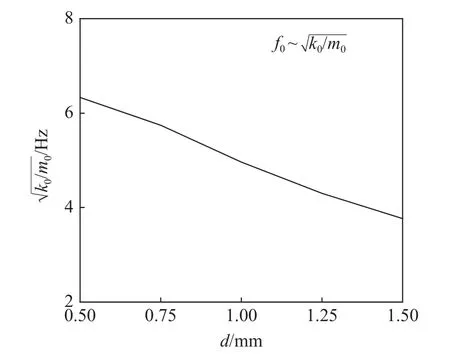
图10 等比例模型的Fig.10 for the equal scale model

4 实验验证

通过本文总结的参数规律,可以根据实际的减振需要设计具体的金字塔点阵圆筒结构,首先确定一组基准模型结构参数,通过归一化频率比较结构的带隙范围和需要的带隙范围的差距,改变基准模型结构的单胞高、单胞宽和杆件的直径之间的比例,使结构的相对带宽和所需要的减振结构的相对带宽一致,然后再调整等比例模型的具体尺寸大小,使结构完全满足所需要的减振效果.

在实验中,选用增材制造技术制备样件,希望结构能够在500～1500 Hz 内能有一个良好的减振性能,以表1 中轴向周期数为8 的金字塔点阵圆筒结构为基准模型,固定结构内接圆半径rc=100 mm,通过上述的设计方法,进行参数调整,最终确定了满足减振要求的结构参数为:rc=100 mm,b=40 mm,h=28.4 mm,d=4 mm,m=8和n=20 .

由于金字塔点阵圆筒结构两端不便于安装和测量,所以在结构的两端加装一个厚度Hb=5 mm,直径Db=296 mm 的圆板.3D 打印时使用的材料为光敏树脂,是一种具有精确和耐久特性的类ABS 的立体光造型树脂,材料参数为密度ρ=1180 kg/m3,弹性模量E=2 GPa .盖板对传递特性的影响如图11所示,发现盖板并不影响整体振动衰减的效果,因此使用这种加盖的结构验证纯金字塔点阵圆筒结构的减振效果是可行的.图12 为实验用金字塔圆筒点阵结构的模型图和实物图.

图11 有无盖板的传递特性曲线对比Fig.11 Comparison of transfer characteristic curves with and without cover

图12 实验用金字塔点阵圆筒结构Fig.12 Pyramid lattice cylinder structure in experiment

随机振动的频带宽,且有连续的频谱,能同时在所有的频率上对试件进行激励,相比于简谐振动仅对某些频率或连续扫频来模拟实际环境振动的影响,随机激励信号的振动实验测试更能反映结构在一定频率范围内的真实减振效果,因此在实验中采用随机激励信号.实验示意图如图13(a)所示,样件的一端通过夹具固定在振动台上,激励端的加速度传感器固定在振动台上,用于接收响应的两个加速度传感器固定在样件的上端面,通过振动台产生随机激励信号,响应端的信号被接收后通过数据处理,得到实验振动传输曲线如图13(b)所示,结果表明,在500～1500 Hz,实验结果与有限元模拟的结果基本一致,结构体现了良好的减振效果,平均的衰减强度达到了50 dB 左右.