线性时间属性中近似安全性和活性的刻画
2022-11-05常玉婷潘海玉
常玉婷, 潘海玉
(桂林电子科技大学 计算机与信息安全学院,广西 桂林 541004)
形式规约作为形式化方法的主要内容,包括性质规约和模型规约[1]。在性质规约中,包含安全性和活性的线性时间属性的规约对于系统验证有着非常重要的作用。直观上说,安全性是指“坏”的事情永远不会发生,活性是指“好”的事情最终会发生[2]。例如,在系统运行时可能会存在多个进程,这些进程不会同时进入临界区,这就保证了系统的安全性;若某个进程在等待区,则它最终会进入临界区,这就保证了系统的活性。
在过去的几十年中,线性时间属性已经得到了广泛研究。Lamport[3]首先引入安全性和活性的概念。随后Alpern等[4]在此基础之上证明了任何一个线性时间属性都可表达为安全性和活性的交集。进一步,Alpern等[5]又从自动机角度对安全性和活性进行研究,首次给出安全性和活性的Büchi自动机刻画。Sistla[6]的研究表明,安全性和活性可通过线性时态逻辑公式进行逻辑刻画。Kupferman等[7]提出了一种检测LTL公式是否是安全性公式的算法,通过给定的安全性构造一个检测坏前缀的Büchi自动机,同时构造了一个紧密自动机对已收集的中间数据进行分析,以防双指数爆炸。除此之外,还有许多有关线性时间属性的研究[8]。
近年来,人们开始研究在概率、模糊和度量等背景下系统的量化验证问题。Kupferman等[9]通过加入概率组件,引入了一种概率坏前缀的概念,以此扩展安全性在实际验证中的适用性。Faran等[10]利用概率给出安全等级的定义,并研究了利用确定性和非确定性自动机及线性时态逻辑公式来确定语言的安全等级的问题。李永明等[11]将经典迁移系统与模糊理论中的不确定性相结合,定义了可能性迁移系统的概念,并提出一种可能性测度方法,在此基础上定义模糊线性时间属性。此外,李永明等[12]将线性时间属性推广到多值逻辑上,根据Heyting代数理论,定义了真值度的概念,并给出安全性和活性在多值逻辑中的定义。Alfaro等[13]提出了度量迁移系统的概念,利用度量空间理论[17]来刻画线性时间属性,并给出了线性时态逻辑在度量空间上的一种扩展形式。除了研究线性时间属性,人们还研究了分支时间属性[18]及模型检测[14-16]等在概率、模糊和度量等背景下的性质。
文献[11]根据格的理论给出真值度的概念,并提出安全性和活性,但基于真值度的计算方式不能很好地刻画系统和属性之间的满足程度。鉴于此,采用度量理论中的线性距离来量化系统多大程度满足线性时间属性,这个距离的值是系统与属性之间距离差值的绝对值,若距离小于一个值,且值的范围为[0,1],则表示系统满足属性的近似程度,值越小表示近似程度越高,当值为0时,表示系统满足这个属性。将线性距离与模糊理论相结合,采用距离刻画系统与属性之间关系的方法,定义出近似安全性与近似活性来量化系统满足其属性的程度。
1 近似线性时间属性



1.1 线性距离
命题距离DP、迹距离DT及线性距离D分别刻画了赋值之间的关系、(V(AP))ω中串之间的关系及FLT属性之间的关系[12],定义分别如下:(V(AP))ω,下列结论成立:

1)Df(σ^,pref(P1))≤α,当且仅当存在σ∈(V(AP))ω,使得D(σ^σ,P1)≤α;
2) 若D(P1,P2)≤α,则Df(pref(P1),pref(P2))≤α。
证明 1)从左推右:设Df(σ^,pref(P1))≤α,则存在ρ^∈pref(P1),有DfT(σ^,ρ^)≤α。 令σ∈(V(AP))ω,且ρ^σ∈P1。将σ^扩展为σ^σ。根据迹距离的定义,

1.2 近似安全性和近似活性
在系统运行过程中,安全性保证“坏”的事情不会发生。经典安全性的定义[2-3]有2种不同的定义形式,分别从好前缀和坏前缀定义而来,具体如下。
1)设P为AP上的线性时间(linear-time, 简称LT)属性。对于所有迹σ∈(2AP)ω,若对任意i≥0,存在σ′∈(2AP)ω,使得σ≤iσ′⊨P,则σ⊨P,称P是一个安全性。
2)设P为AP上的LT 属性,若对所有迹σ∈(2AP)ω,且σ∉P,存在σ^∈pref(σ),使得对任意σ′∈(2AP)ω,σ^σ′∉P,则称P是一个安全性。这里称σ^为P的一个坏前缀。
通过引入距离阈值α,将好前缀的定义从经典安全性推广到近似安全性。具体定义如下。
定义1 设P为AP上的FLT 属性,α∈[0,1]。对所有σ∈(V(AP))ω,若对任意i≥0,存在σ′∈(V(AP))ω,使得D(σ≤iσ′,P)≤α,则D(σ,P)≤α,称P是一个α-安全性。
对于一个0-安全性P,由定义1 知,对任意i≥0,存在σ′∈(V(AP))ω,使得D(σ≤iσ′,P)=0,则D(σ,P)=0,即σ∈P。因此,0-安全性就是经典的安全性。
相较于安全性,活性保证“好”的事情最终会发生。经典活性的定义[3]为:设P为AP上的LT 属性,若对任意σ^∈(2AP)*,存在σ′∈(2AP)ω,使得σ^σ′⊨P,则称P是一个活性。
与近似安全性类似,以下给出活性的一种定量推广形式——α-活性。
定义2 令α∈[0,1],P为AP上的FLT属性。若对任意σ^∈(V(AP))*,存在σ′∈(V(AP))ω,有D(σ^σ′,P)≤α,则称P是一个α-活性。
对于一个0-活性P,由定义2知,对任意σ^∈(V(AP))*,存在σ′∈(V(AP))ω,有D(σ^σ′,P)=0,即σ^σ′∈P。因此,0-活性就是经典的活性。
2 近似线性时间属性的逻辑刻画
模糊迁移系统是一个五元组F=(S,→,s0,AP,L),其中:S为状态集合;→⊆S×S为迁移关系;s0∈S为初始状态;AP为原子命题集合;L:S→V(AP)为标记函数。
由定义知,模糊迁移系统和经典迁移系统的主要区别是标记函数。根据文献[2],经典迁移系统的标记函数为L:S→2AP,状态上的标记是原子命题集合中的元素。而本研究的模糊迁移系统,其状态上的标记是原子命题AP的一个赋值。
模糊迁移系统可表示为带标签的有向图,如图1所示。图中的圆圈表示系统的状态,圆圈中的符号代表该状态名,圆圈旁边的部分表示该状态上原子命题的赋值,若赋值为0,则省略该原子命题。例如,状态s1是模糊迁移系统的一个状态,s1的标记函数为L(s1),则根据图1可知,L(s1)(p)=0.7,L(s1)(r)=0.4。在状态s2中原子命题r赋值为0,故省略。图1中的有向边表示状态之间的迁移,一条无出发结点的有向边指向的状态为初始状态,如状态s0是该模糊迁移系统的初始状态。
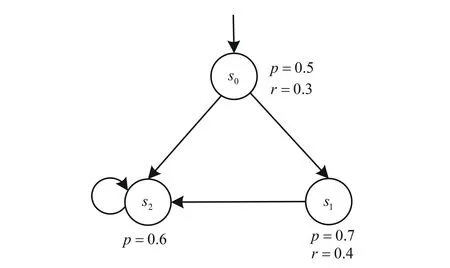
图1 模糊迁移系统
定义3[19]给定原子命题集AP,AP上的FLTL公式的语法递归定义为
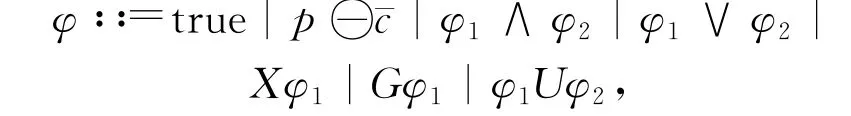
其中,p∈AP,c∈[0,1]。
以下给出FLTL 公式在(V(AP))ω上的语义解释。

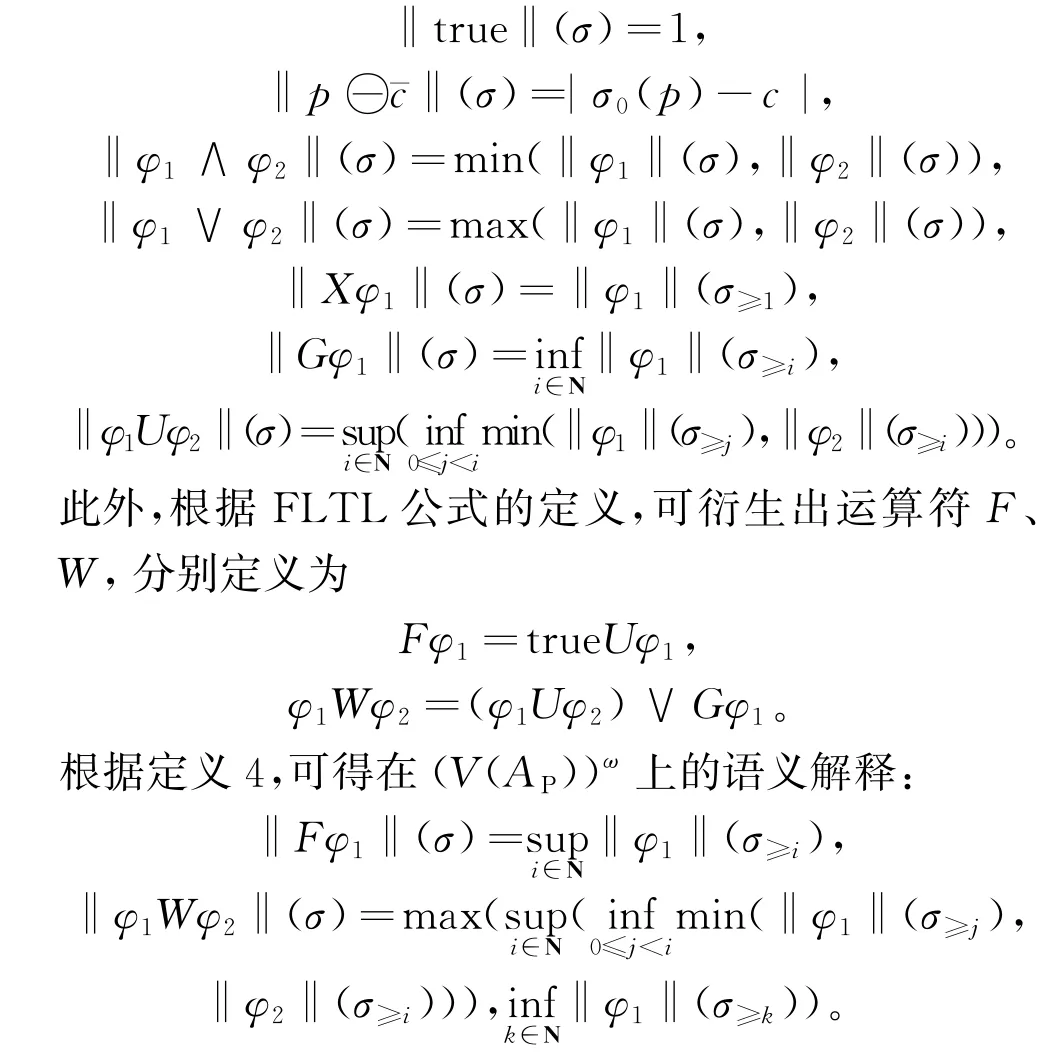
给定一个FLTL公式φ和阈值α∈[0,1],φ在α约束下表示一个FLT属性Lα(φ),定义为

若Lα(φ)是一个α-安全性,则称φ为α-安全性公式;同样,若Lα(φ)是一个α-活性,则称φ为α-活性公式。因当α取值为0时,α-安全性和α-活性即为经典的安全性和活性,因此,此时α-安全性公式和α-活性公式为安全性公式和活性公式。
定理1 设p∈AP,c∈[0,1],且α∈[0,1]。在FLTL公式中,以下结论成立:
1)true和p⊖c-是α-安全性公式;
2)若φ1、φ2 是α-安全性公式,则φ1 ∧φ2,φ1 ∨φ2,Xφ1,Gφ1 和φ1Wφ2 也是α-安全性公式。
这里只证明p⊖c-。 其余证明与文献[19]的证明类似。

设对所有σ∈(V(AP))ω,D(σ,Lα(φ))>α,则对任意ρ∈Lα(φ),有DT(σ,ρ)>α。 根据迹距离DT的定义,存在i∈N,使得DP(σi,ρi)>α。 设i=0时,DP(σ0,ρ0)≤α。此时,对任意的p∈AP,|σ0(p)-ρ0(p)|≤α。 将ρ0扩展为无限迹ρ′=ρ0σ1σ2…,则

要判断φ是否是0.2-安全性公式,只需判断Lα(φ)是否为0.2-安全性。设σ∈L0.2(φ)且σ∉P,则存在j≥0,使得σj(p)≥0.8且σj(r)≥0.8。根据定义4,
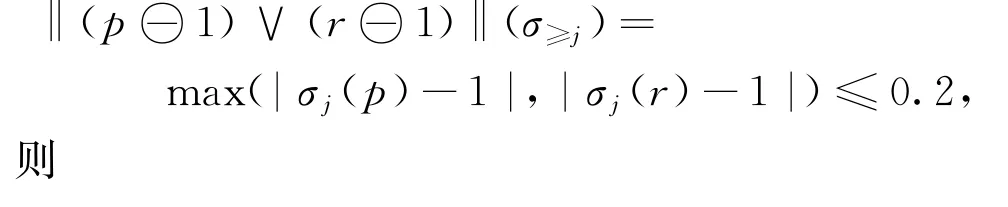

定理2 令α∈[0,1]。在FLTL公式中,以下结论成立:
1)当α∈[0,1)时,true是α-活性公式;
2)p⊖c-是α-活性公式;
3)若φ1 和φ2 是α-活性公式,则φ1 ∧φ2 是α-活性公式;
4)若φ1 或φ2 是α-活性公式,则φ1 ∨φ2 是α-活性公式;
5)若φ2是α-活性公式,则φ1Uφ2和φ1Wφ2都是α-活性公式;
6)若φ1是α-活性公式,则Xφ1和Fφ1都是α-活性公式。

2)令φ=p⊖c-。设φ不是α-活性公式,则存在^σ∈ (V(AP))*,对 任 意σ′ ∈ (V(AP))ω,有D(^σσ′,Lα(φ))>α。令^σσ′=σ。由线性距离D的定义知,对任意ρ∈Lα(φ),TD(σ,ρ)>α。进一步,由迹距离DT的定义,存在i≥0,使得DP(σi,ρi)>α。又根据定理1的证明,当i=0时,DP(σ0,ρ0)>α,因此
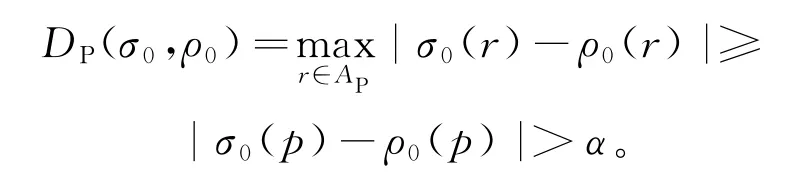

因此φ是α-活性公式。
3)设φ1 和φ2 是α-活性公式。令φ=φ1 ∧φ2,σ∈Lα(φ),根据Lα(φ)的定义,‖φ‖(σ)>α,即

所以‖φ1‖(σ)>α且‖φ2‖(σ)>α,即σ∈Lα(φ1)且σ∈Lα(φ2)。因为φ1和φ2是α-活性公式,则对任意^σ∈(V(AP))*,存在σ′∈(V(AP))ω,有

因此φ是α-活性公式。
4)设φ1 或φ2 是α-活性公式。令φ=φ1 ∨φ2,σ∈Lα(φ),根据Lα(φ)的定义,‖φ‖(σ)>α,即
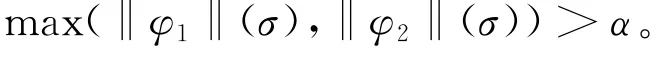
所以有‖φ1‖(σ)>α或‖φ2‖(σ)>α,即σ∈Lα(φ1)或σ∈Lα(φ2)。不妨设σ∈Lα(φ1)。当φ1是α-活性公式时,对任意^σ∈(V(AP))*,都存在σ′∈(V(AP))ω,有D(^σσ′,Lα(φ1))≤α。因此,存在ρ∈Lα(φ1),使得DT(^σσ′,ρ)≤α。故

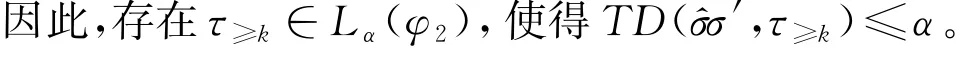

φ1是α-活性公式,所以Fφ1 是α-活性公式。
例2 设AP={p,r},V(AP)为AP在[0,1]f上所有赋值的集合。令P是一个0.5-活性,对所有σ∈P满足:任意i≥0,σi(p)<0.5或σi(r)<0.5。现在使用FLTL公式描述该属性。令


根 据L0.5(φ)的 定 义,σ∈L0.5(φ)。 故P⊆L0.5(φ)。综上所述,Lα(φ)=P成立,所以(p⊖1)U(r⊖1)是0.5-活性公式。
3 实例
考虑一个由墙、窗户、加热器和控制器组成的房间。控制器的目的是尽可能将温度维持在用户舒适的范围。因为“舒适”是一个模糊的概念,人们不能很精确地将“舒适”的意思描述出来,每个人对“舒适”的描述也会不一样,所以可以将“舒适”一词通过以下模糊集的定义来解释[21-23]:

其中:Te(t)为室外温度;T(t)为当前室内温度;E(t)为特定于墙体和窗户的热交换系数;H(t)为加热器的功率。
假设温度控制器可接收的温度范围为10~45℃,当室内温度低于17℃时,加热器开启;当室内温度高于24℃时,加热器关闭;当室温处于20~22℃时,加热器处于睡眠模式,当处于睡眠模式的时间超过60 min时,加热器将自动关闭。设置控制器每30 min接收一次温度读数,然后判断是否对加热器进行开或关或睡眠的操作。
对房间温度的舒适度演化进行建模。设

其中,S={s0,s1,s2},AP={t,c},其中:状态s0表示加热器处于关闭状态;状态s1表示加热器处于加热状态;状态s2表示加热器处于睡眠状态;c表示当前温度下用户的舒适度;t表示温度系数(即当前温度/100),AP的赋值是在[0,1]范围内。为了方便计算,所有的数值均保留小数点后3位。设加热器开启的功率为0.06℃/min,睡眠模式的功率为0.03℃/min。墙体和窗户的热交换系数为0.005℃/min。令i≥1,可使用公式[22]

计算大约30imin后的室温,再通过x求μc。 公式所计算的具体值如表1所示。
根据表1,可以构建FTS。如图2所示,此时室温为16℃,加热器处于关闭状态。由于温度低于17℃,开启加热器,到达状态s1。在30 min后,温度控制器接收当前室温,根据上述公式,计算可得室温为17.65℃,此时用户舒适度仍为0,继续处于状态s1。通过计算,在i=4,即120 min后,室内温度将升至约20.3℃,此时用户舒适度约为0.767,此时加热器切换为睡眠模式,到达状态s2。 由于加热器处于睡眠模式的时间超过60 min,加热器i=7时切换为关闭状态s1。这里不再考虑在加热器从睡眠模式关闭后的情况。

图2 FTS

表1 温度控制器接收t及s和c的关系
所构建的FTS有2个属性需要考虑:一是“安全性”,就是用户一直感到舒适;二是“活性”,就是最终会到达一个合适的舒适度范围。假设满足安全性的“好”的舒适度范围为[0.6,0.9],而满足活性的合适的舒适度范围为[0.6,1]。
首先考虑安全性的规范。根据图2,令P是一个FLT属性,且P是一个0.1-安全性,对所有σ∈P满足:任意i≥0,0.6≤σi(c)≤0.9。因为“安全性”是要保证一直在舒适度的范围,所以使用FLTL公式中的G描述该系统所刻画的安全性。令φ=G(c⊖1),根据Lα(φ)的定义,

因此,G(c⊖1)是0.1-安全性公式。0.1-安全性表示:该系统所满足的舒适度范围和满足安全性的舒适度范围之间,只要保证在0.1误差以内,都可视为是“安全”的。
根据图2,令P为一个FLT 属性,且P是一个0.3-活性,对所有σ∈P满足:存在i≥0,σi(c)<0.7。因为“活性”是最终要处于舒适的状态,所以使用FLTL公式中的F描述该属性。令φ=F(c⊖1),根据Lα(φ)的定义,所以,σ∉L0.3(φ),这与假设矛盾。故σ∈P,L0.3(φ)⊆P。 设σ∈P,则存在i≥0,σi(c)<0.7。根据定义4,
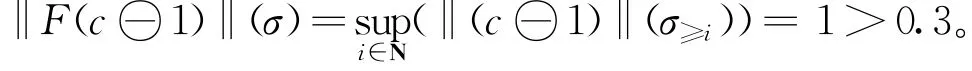

根据L0.3(φ)的 定 义,σ∈L0.3(φ)。 故P⊆L0.3(φ)。综上所述,Lα(φ)=P成立,所以F(c⊖1)是0.3-活性公式。0.3-活性表示:该系统所满足的舒适度范围和满足活性的舒适度范围之间,只要保证在0.3误差内,都可以视为系统满足该属性。
4 结束语
研究了模糊背景下的近似安全性和近似活性及其逻辑和自动机刻画。通过引入距离阈值α∈[0,1],定义了α-安全性和α-活性,并通过一些例子来描述所给出的定义,最后通过模糊线性时态逻辑公式给出近似安全性和近似活性的逻辑刻画。下一步将考虑研究模糊背景下近似安全性和近似活性相关验证算法及自动机的刻画。
