谐振接地系统两点同相接地故障暂态特征及选线

刘映彤，黄纯，袁静泊，闫森

(湖南大学 电气与信息工程学院，湖南 长沙 410082)

0 引言

谐振接地系统发生单相接地故障时，短期内系统可带故障运行，在中国广泛应用[1-5]。但在带故障运行期间，故障线路处可能会发生绝缘击穿，进而形成两点故障[6-10]。此外，由于雷雨等天气的影响，线路间也容易发生两点同相同时接地故障[11-14]。发生两点同时接地故障时，由于线路分流，故障线路的零序电流小于单点接地情况，不利于选线[15]。特别是对于两故障点过渡电阻相差较大情况，同时将两条故障线路选出的难度更大[16]。

近年来，对配电线路两点接地故障的研究逐渐增多。文献[17]对小电阻接地系统发生两点及多点接地情况进行了研究，分析得到多点接地时的稳态故障特征，提出了一种基于零序电流幅值和相位的保护方法。文献[18]对谐振系统中单相接地故障引发的稳态过电压进行了理论分析，并结合实际多条线路相继接地故障案例，提出了具有实用价值的解决措施。文献[19]研究了不接地系统发生同相两点接地时的故障工频特征，通过公式推导得到至少有1 条故障线路零序电流相位与健全线路相反的规律，从而提出了基于两阶段无功功率方向的选线方法。文献[20]对小电流接地系统中分别发生同相和异相两点相继接地进行仿真分析，利用零序电流幅值相位依次选出2 条故障线路。上述研究大多数针对工程实例，并未研究两点接地故障暂态特征，并且采取的选线思路可概括为：先切除故障特征较为明显的线路，再切除第2 条故障特征较为微弱的线路，无法同时选出2 条故障线路。

本文针对配电网谐振接地系统，建立并化简两点同相接地故障等效零序网络，分析两点同相接地故障的暂态特征，利用线路零序电流暂态量与母线零序电压暂态量的关系，形成适用于两点同相接地故障的新方法。该方法可同时选出两条故障线路，对于高阻故障同样适用。

1 谐振接地系统两点同相故障分析

1.1 两点同相接地零序网络

两点同相接地故障依据故障时间的不同可分为两点同时接地故障和两点相继接地故障，本文主要研究两点同时接地故障问题，其零序网络可等效如图1 所示，设图1 中零序电流流向为正方向。

图1 中：U˙f1、U˙f2分别为两接地点的虚拟电源零序电压；C01，C02， ···，C0k分别为健全线路的对地零序电容，Cf1、Cf2分别为两故障线路的对地 零 序 电 容，C0∑=Cf1+Cf2+C01+···C0k；Rf1和Rf2分 别 为 接 地 点1 和 接 地 点2 的 接 地 电 阻；I˙1，I˙2，···，I˙k为 健 全 线 路 始 端 的 零 序 电 流；I˙f1和I˙f2为两故障线路始端的零序电流；I˙L和L0分流别为中性点的零序电流和消弧线圈电感；U˙0为母线零序电压。

发生两点同相接地故障时，两接地点的虚拟电源U˙f1、U˙f2相 等，且U˙f1=U˙f2= -U˙A，其中U˙A为故障相电压。根据戴维南和诺顿等效定理，可将图1 进行化简，结果如图2 所示。

图1 两点同相接地故障等效零序网络Fig. 1 Equivalent zero-sequence network for two-point grounding fault on same phase

图2 网络化简Fig. 2 Simplified network

图2 中，I˙f=-U˙A/(3Rf1//3Rf2) ，U˙f=-U˙A，Rf=3Rf1//3Rf2，Cf=Cf1+Cf2，I˙f=I˙f1+I˙f2。

可以看出，两点接地故障可以等效为单点接地故障，其过渡电阻为两过渡电阻的并联，其对地电容为2 条故障线路的对地电容之和。根据图2的等效网络可列出方程为

根据两点接地故障过渡电阻的不同，系统将呈现不同状态下的谐振过程，接下来对欠阻尼和过阻尼的暂态过程进行分析。

1.2 过阻尼状态暂态计算

流过健全线路始端的零序电流为

1.3 欠阻尼状态暂态计算

当特征根为共轭复根时，即当过渡电阻满足式（14）时，则为欠阻尼状态[22]，此时线路的电容电流较小或两故障点过渡电阻的并联值较大，即

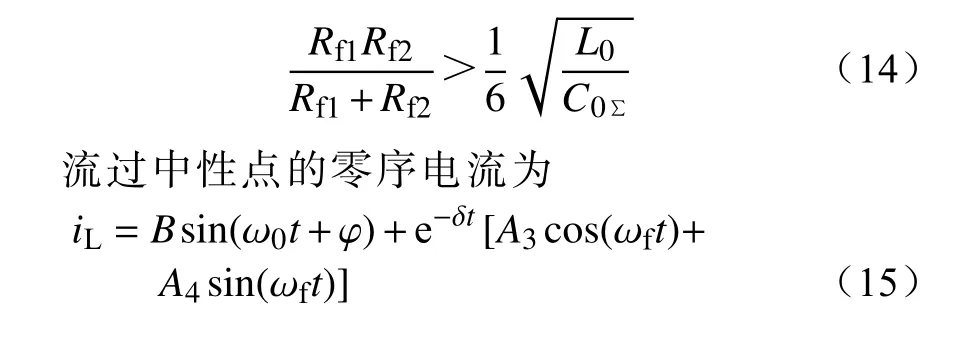
由以上推导可知：线路零序电流及母线零序电压由暂态量和稳态量组成。过阻尼状态下，稳态量为工频，暂态量为衰减的直流分量；在欠阻尼状态下，稳态量为工频，暂态分量为衰减的交流量。

由式（13）、式（20）可知故障线路始端零序电流暂态量为零序电压暂态量与零序电压暂态量导数的线性组合，非故障线路始端零序电流暂态量与零序电压导数暂态量成正比。

零序电压的暂态量和两接地点过渡电阻的并联值、系统零序电容和消弧线圈电感值相关。由于线路分流作用，故障线路的零序电流暂态分量不仅与本身线路过渡电阻值相关，还与另一个故障点的电阻相关。当两接地点过渡电阻相差较大时，两故障线路的零序电流大小相差显著。

2 适应两点同相接地故障的选线方法

根据上述结论可知两点接地故障的零序电流及零序电压的暂态特征与单点接地故障暂态特征一致[23]，故障线路零序电流暂态量可表示为

然而仅根据各线路Sn积分的大小差异，无法保证能够同时选出2 条故障线路，特别是当故障点过渡电阻为高阻的情况，其线路Sn的积分与健全线路相近，无法准确判断出2 条故障线路。

健全线路的过渡电阻趋向于无穷大，而故障线路的过渡电阻可求出其实际值，且远小于健全线路。因而故障线路过渡电阻满足关系式（29）（式中Rfset为过渡电阻阈值），即

而健全线路的过渡电阻远大于阈值，不满足式（29），因而可依此判据选出故障线路。接地过渡电阻一般小于10 kΩ，故Rfset可取10 kΩ。

依据上述原理，结合故障线路与健全线路Sn积分的大小差异以及故障线路的过渡电阻小于设定阈值的2 个判断依据，由此构成适用于两点接地故障的选线判据，可靠性高。

3 故障选线流程

综合以上分析，两点同相接地故障选线方法的实现步骤如下，对应流程如图3 所示。

图3 故障选线流程Fig. 3 Flow chart of fault line selection algorithm

（1）采集系统母线零序电压U0和各线路始端零序电流I0n。

（2）若 |U0|＞U0set（其中U0set为零序电压阈值），则开始采样录波。采样数据为接地故障后20 个周期的母线零序电压u0(t)和出线零序电流i0(t) （t=1,2···N，N为采样总数）。

（3）利用零序电流和零序电压的瞬时值减去稳态值获得暂态量。将采样得到的零序电流1～10 个周期减去11～20 个周期得到零序电流暂态量i0_T(t)；将零序电压的1～10 个周期减去11～20 个周期波得到零序电压暂态量u0_T(t)。

（4）对零序电压暂态量u0_T(t)进行差分运算得到零序电压导数暂态量 du0_T/dt，再根据式（26）（27）计算求得各馈线过渡电阻Rfn和Sn。

（5）将各馈线的过渡电阻与设定阈值进行比较，若有且只有1 条线路的过渡电阻小于设定阈值，且该线路Sn的值最大，则为单点接地，对应线路为故障线路。

（6）若有2 条线路的过渡电阻小于设定阈值，这2 条线路的Sn均大于其他线路，且此2 条线路中过渡电阻较小的线路对应的Sn大于过渡电阻较大的线路，则判定发生两点同相接地故障，两线路为故障线路。

4 仿真验证

利用Matlab/Simulink 软件搭建一配电网谐振接地系统，其中馈线类型、数量和长度如图4 所示。设置消弧线圈过补偿10%，电感值为1.276 H，架空线和电缆的电阻、电感和电容参数如表1 所示。

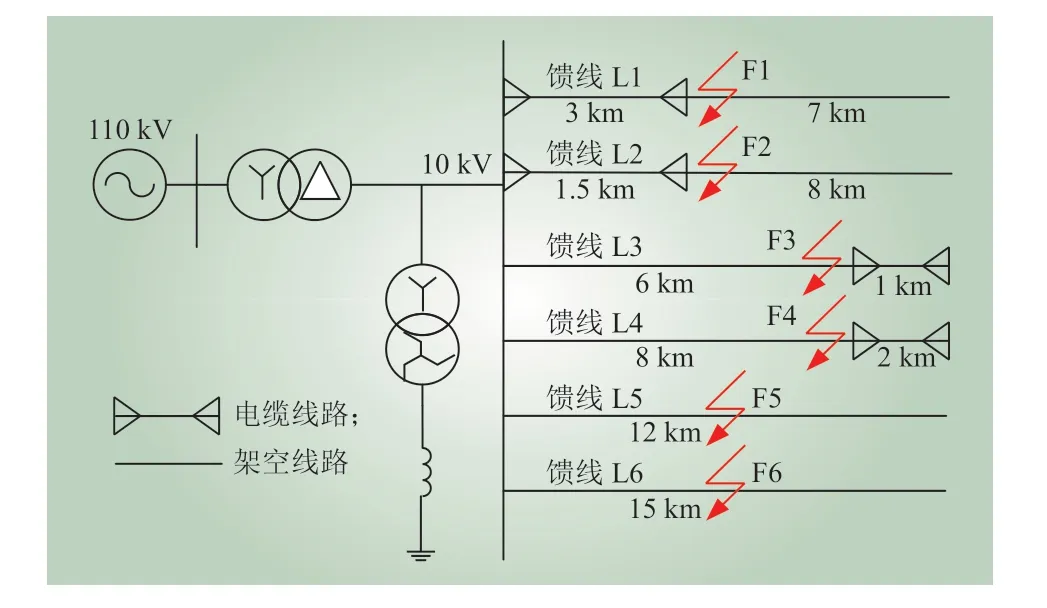
图4 系统模型Fig. 4 System model

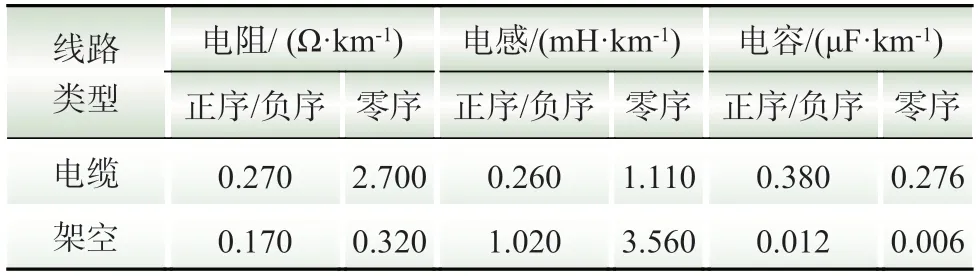
表1 系统架空线路和电缆参数Table 1 System overhead line and cable parameters

4.1 单点接地与两点接地故障特征对比

设置 F1、 F2两点同时发生接地故障，两点过渡电阻分别为10 Ω 、 1 000 Ω，故障合闸角均为0°。图5 为各出线的零序电流波形。故障线路和健全线路的零序电流稳态量方向相同，所以仅利用零序电流稳态量无法判别故障线路。此外，过渡电阻大的馈线的零序电流波形与健全线路相似，且其零序电流幅值较小。

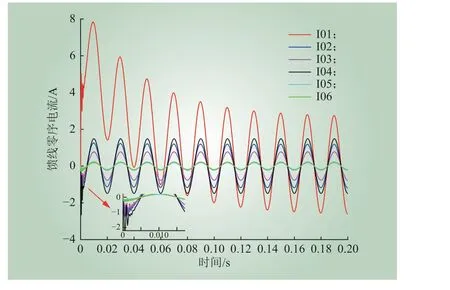
图5 两点同相接地零序电流Fig. 5 Zero-sequence current of two-point grounding fault on same phase

为了与单点故障进行对比，设置 F2发生接地故障，故障点的过渡电阻为1 000 Ω，得到图6 所示的各出线零序电流。

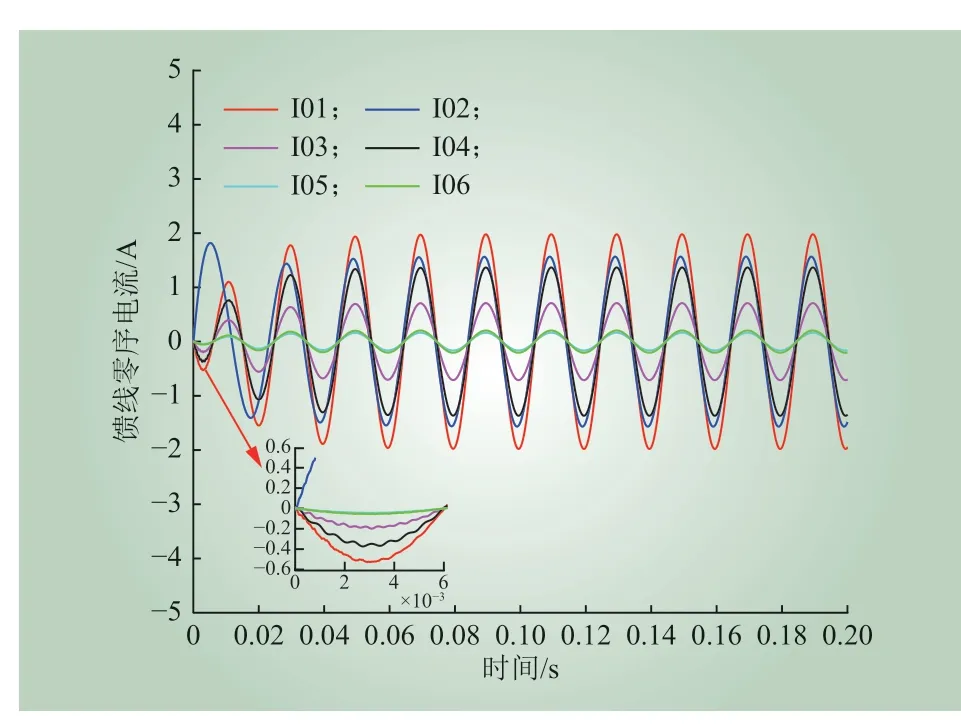
图6 单点接地零序电流Fig. 6 Zero-sequence current of single-point grounding fault

将图5 和图6 中馈线2 零序电流对比分析可知：在两点同相接地故障中，馈线2 的零序电流因为受另一故障点的影响，其大小和相位均发生改变，且其零序电流特征与健全线路的零序电流特征差异变小，所以利用零序电流幅值或相位进行选线的方法不适用于两点接地情况。

4.2 两点同相接地故障选线

在配电网不同故障点（F1～F6）处设置不同的过渡电阻，仿真获得在不同情况下的参数估计和故障选线结果，其中，线路零序电容估算和故障线路过渡电阻估算结果如表2 所示，各线路的过渡电阻估计值及Sn值如表3 所示。

由表2 可知，无论是单点接地还是两点同相接地，利用最小二乘法估算出的各线路零序电容值与实际线路参数接近，故障线路的过渡电阻估计值接近于实际过渡电阻数值，验证了参数估计的准确性。

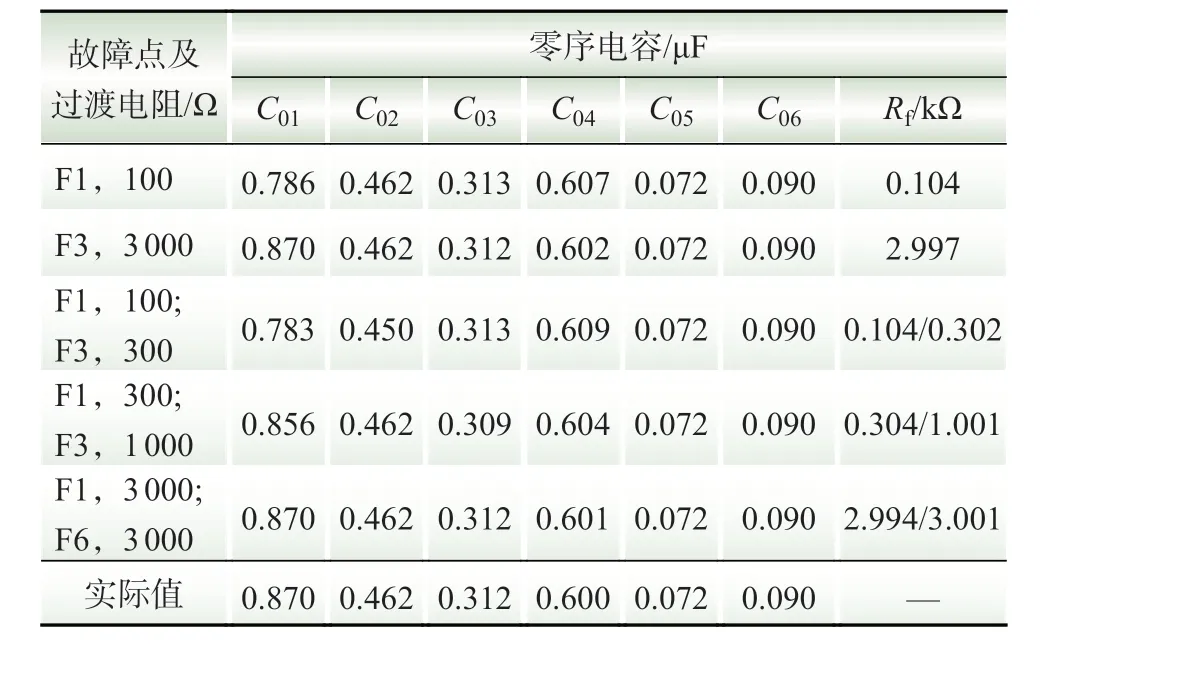
表2 不同工况下的线路零序电容和故障线路过渡电阻估算Table 2 Estimation of line zero-sequence capacitance and fault line transition resistance under different conditions

由表3 可知，在不同馈线、不同故障点和不同过渡电阻状态下，健全线路过渡电阻估计值远大于阈值，而两故障线路过渡电阻估计值接近实际值且均小于阈值，且无论两过渡电阻值相差是否较大，均能较准确地估算两点的过渡电阻。无论发生何种类型的接地故障，故障线路的Sn值与健全线路相差很大，且故障馈线的电阻越大，其对应的Sn值越小，但仍大于健全线路。因此，该选线方法不仅适用于单点接地故障，同样也适用于两点接地故障，对于高阻故障情况也能正确识别。

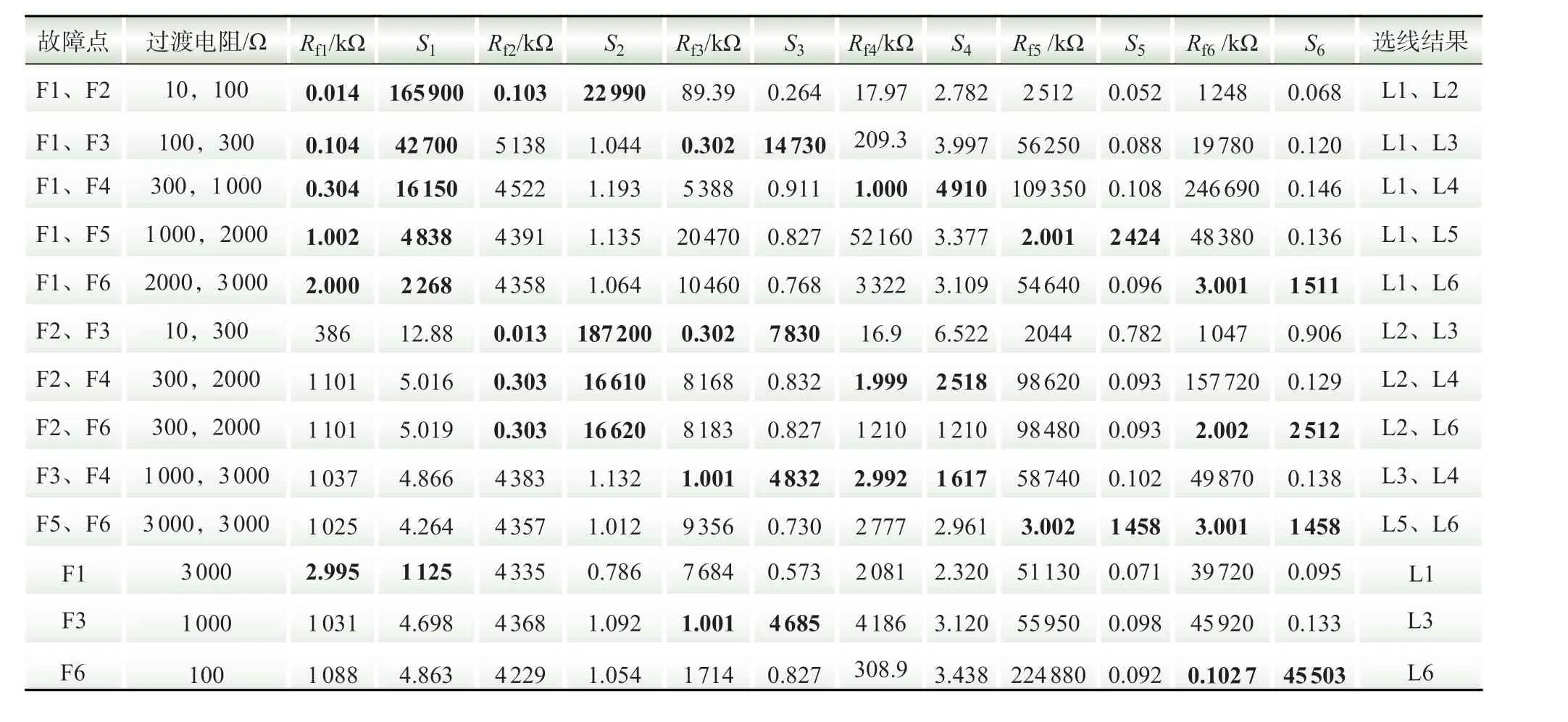
表3 不同工况下的选线结果Table 3 Line selection results under different operating conditions

4.3 与已有选线方法的对比

相电流突变量法[24]、暂态无功功率法[25]是目前小电流接地故障选线准确率较高、应用较广的2 种方法。采用这2 种方法及本文方法进行两点同相接地故障选线，并比较3 种方法的性能。

设定故障同时发生在图4 的 F1、 F2两点，改变故障点过渡电阻值进行仿真，不同方法的比较结果如表4 所示。由表4 可知，在两点同相接地故障下，相电流突变量法不适用于高阻故障，且当两故障点过渡电阻相差较大时，只能选出故障特征较明显的线路；暂态无功功率法在两点接地过渡电阻相差较大时，也只能选出1 条故障线路，但适用于高阻故障，适用性比相电流突变量法好；本文方法能准确选出2 条故障线路，适应性更好。

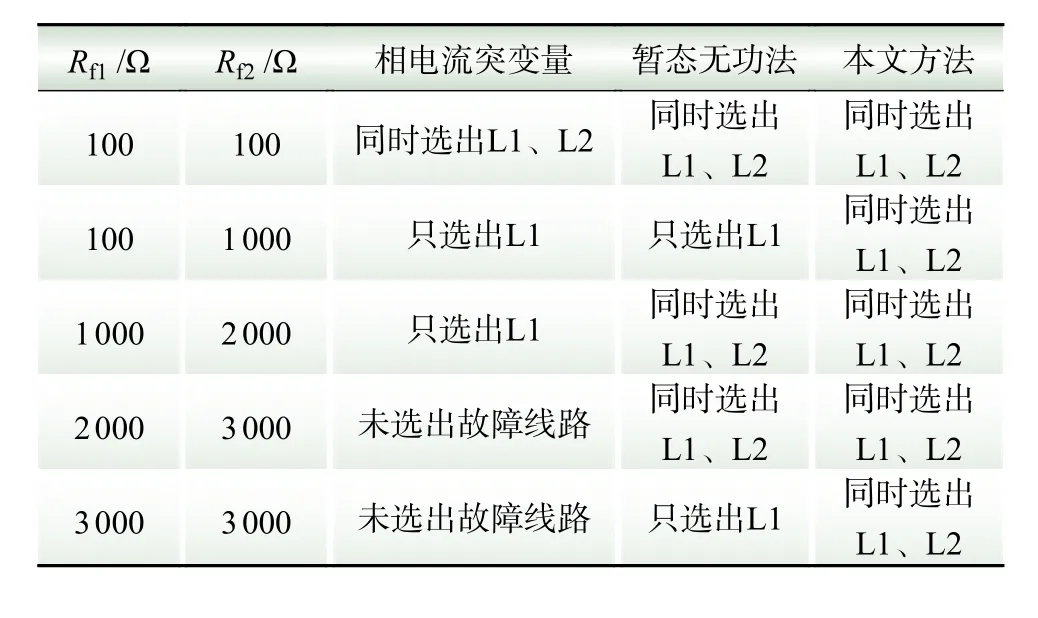
表4 不同方法的选线结果Table 4 Line selection results with different methods

5 结语

谐振接地系统发生两点同相接地故障时，其故障特征与单点接地不完全相同。本文对两点接地故障系统的暂态特征进行分析，并提出了一种适应于两点接地故障的选线方法。理论分析和仿真结果表明：（1）该选线方法利用线路零序电流和零序电压暂态量，不受故障位置和线路类型的影响，抗干扰能力强。（2）该选线方法可适用于单点和两点接地故障，且对于高阻接地故障同样适用，在各种故障情况下均能准确选线，仿真结果证明了该方法的可靠性。（3）本文方法能够同时准确选出2 条故障线路，且对于两点过渡电阻值相差较大情况同样适用，可提高选线的速度和准确性。