基于加窗FFT 的风电场自适应振荡抑制策略

2022-11-05苗硕李奇南查鲲鹏李兰芳曹建春张帆

中国电力 2022年10期

苗硕，李奇南,，查鲲鹏，李兰芳,，曹建春，张帆,

(1. 国网电力科学研究院有限公司，江苏南京 211106；2. 北京市直流输配电工程技术研究中心（中电普瑞电力工程有限公司），北京 102200；3. 中电普瑞科技有限公司，北京 102200)

0 引言

在“双碳”目标的背景下，风力发电技术快速发展。风电机组大量并网给电力系统的稳定性带来很大的挑战。近年出现的典型风电场振荡案例主要包括河北沽源双馈风电场和新疆哈密直驱风电场的次同步振荡、德国北海海上风电场以及中国新疆和广东某风电场的中高频振荡[1-4]。电力系统的电力电子化造成的1 Hz 至数千Hz 的宽频振荡会造成系统功率大幅波动，大量机组脱网，严重威胁电力系统的安全稳定运行。

针对宽频振荡问题，国内外学者对相关分析方法和抑制策略进行了大量研究。阻抗分析法是分析互联系统稳定性的常用方法。文献[5-7]对直驱风机(permanent magnet synchronous generator ,PMSG)和柔性直流换流站的阻抗模型做出详细推导。当前的振荡抑制策略主要可以分为3 类。（1）改变系统参数。文献[8]表明双馈风机和直驱风机混合安装可以提高系统稳定性；文献[9-10]提出了风电场经柔直并网的控制参数设计方法；文献[11]提出了直驱风电场接入弱电网的各控制环节参数设计方法。改变电气参数适合于系统规划阶段，不适用于已投运的工程。（2）附加灵活交流输电(flexible AC transmission system，FACTS)装置。文献[12]提出利用静止同步补偿器抑制双馈风电场次同步振荡。附加FACTS 装置虽适用于已投运工程，但增加了额外投资。（3）附加阻尼控制。文献[13]提出了基于电网阻抗检测的阻抗重塑策略，但计算阻抗过程烦琐；文献[14]提出利用附加比例谐振控制器抑制风电场次同步振荡的策略，但没有频率自适应功能，有一定的局限性；文献[15]利用非线性控制器替代比例积分控制器的方法，但增加了系统分析的复杂度；文献[16]提出针对LCL 型并网逆变器的高频阻抗重塑方法。相较前两类抑制策略而言，附加有源阻尼控制是一种有效易行的方法，目前广受学者青睐。但附加有源阻尼控制方法也有一定缺陷，当系统振荡频率改变时，需要重新对其中的关键参数做调整，否则可能会造成抑制效果降低甚至失效[17]。

风电场运行工况多变，发生振荡时振荡频率变化范围较大，为确保控制器可以适应振荡频率多变的系统，可以通过对电网振荡频率的实时检测，在线调整控制器的参数。快速傅立叶变换(fast Fourier transform, FFT)是当前谐波和间谐波的主要检测方法，但FFT 存在频谱泄漏、栅栏效应和谱线干涉等问题，会造成频率检测出现较大误差。为解决FFT 的固有缺陷，通常采用加窗插值算法，常用的窗函数主要包括汉宁窗、汉明窗和布莱克曼窗等。目前，通常将窗函数和插值算法结合起来对谐波、间谐波进行分析。插值算法主要包括单谱线插值、双谱线插值及多谱线插值。文献[18]提出了利用六谱线插值提高频率检测精度的方法。但提高频率检测精度的同时增加了算法的复杂度，计算量增大。文献[19]提出可变窗函数宽度的滑窗频率检测法。文献[20]提出不依赖于窗函数的迭代加窗插值算法。文献[21]结合了基于遗传算法的组合余弦窗的算法。通过插值算法可以减少栅栏效应对检测结果的影响，从而提高检测精度。上述文献提出的基于加窗FFT 的电力系统谐波和间谐波检测改进算法都是基于足够长的数据长度所做的频率检测研究，实际上频率检测的速度和精度无法兼顾。自适应控制器的控制目标是对系统发生振荡时快速做出动作，算法需要使FFT 在拥有尽可能小的数据长度的情况下较为准确地对振荡频率进行估计。

针对上述问题，本文建立了直驱风机的阻抗模型，基于阻抗稳定判据分析了直驱风机接入交流系统的中高频稳定性，从阻抗的角度解释了准比例谐振(quasi-proportional resonance, QPR)控制器抑制中高频振荡的机理，进而提出基于加窗FFT的自适应QPR 控制器的振荡抑制策略，以实现控制器的在线快速动作。最后在PSCAD/EMTDC 上对比了基于加窗FFT 和传统FFT 策略的振荡抑制效果，验证了所提抑制策略的优越性。

1 直驱风机阻抗建模

由于直流侧电容的解耦作用，直驱风机阻抗可以简化为网侧逆变器和受控电流源，并且考虑到直流电压外环控制带宽远低于本文研究中高频频段(500～2 000 Hz)[22]，将直驱风机模型简化为如图1 所示的结构，其中涉及直驱风机的电流环、锁相环(phase-locked loop, PLL)以及延时等环节，另外主电路滤波器采用LC 型。通过阻抗建模，可以为后续提出振荡抑制策略奠定理论基础。

图1 直驱风机主电路及控制框图Fig. 1 Main circuit and control block diagram of PMSG

定义PMSG 端口阻抗ZPMSG(s)为端口扰动电压与流入直驱风机的扰动电流的比值，即

式中：KT为机端升压变变比；n为风机台数。

本文所研究的PMSG 的主电路参数以及控制参数如表1 所示。根据式（4）和表1 中的参数绘制出阻抗特性曲线，并在PSCAD/EMTDC 中搭建频率扫描模块扫频验证，结果如图2 所示。由图可知，理论计算结果和仿真扫频结果基本一致，验证了阻抗建模的准确性。

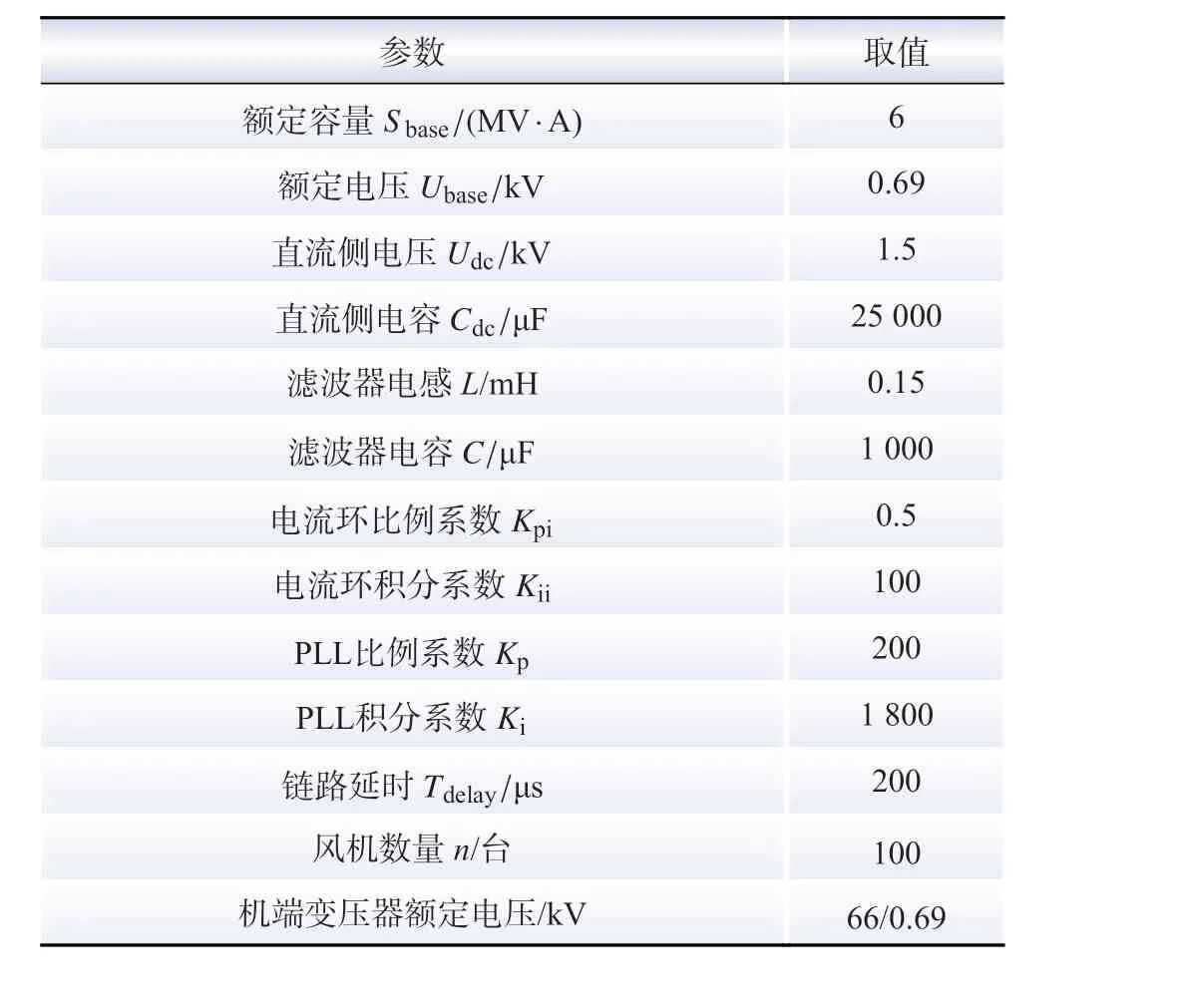
表1 PMSG 主电路参数及控制参数Table 1 Main circuit and control parameters of PMSG

图2 PMSG 阻抗理论计算与扫频结果Fig. 2 Theoretical calculation and frequency scanning results of PMSG impedance

2 中、高频振荡分析

根据奈奎斯特阻抗稳定判据，两互联系统失稳的条件[13]为

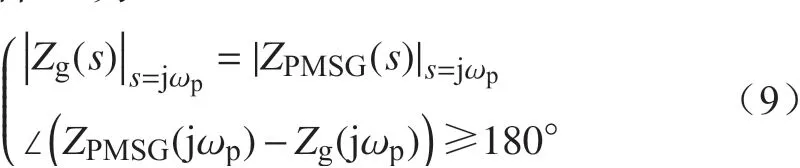
式中：Zg(s)为电网侧的阻抗； ωp为扰动量角频率。

图3 为PMSG 和交流系统的阻抗特性曲线，红色、蓝色、黄色曲线分别代表PMSG 并网台数为30 台、65 台和100 台时的阻抗特性曲线，绿色曲线代表交流系统阻抗特性曲线。交流系统等效阻抗取电阻为0.5 Ω，电感取5 mH。由图中幅频特性可知风电场并网台数为30 时，与交流系统阻抗特性曲线相交于1 083 Hz；风电场并网台数为6 5 时，相交于7 7 2 H z；风电场并网台数为100 时，交于656 Hz。由相频特性可知，350 Hz 处风机相角为-98.2°，并随频率增加变化不明显，一直处于-90°以下。此时，交流系统相频特性接近90°。因此，当幅频特性交点大于350 Hz 时，风电场存在中高频振荡风险。

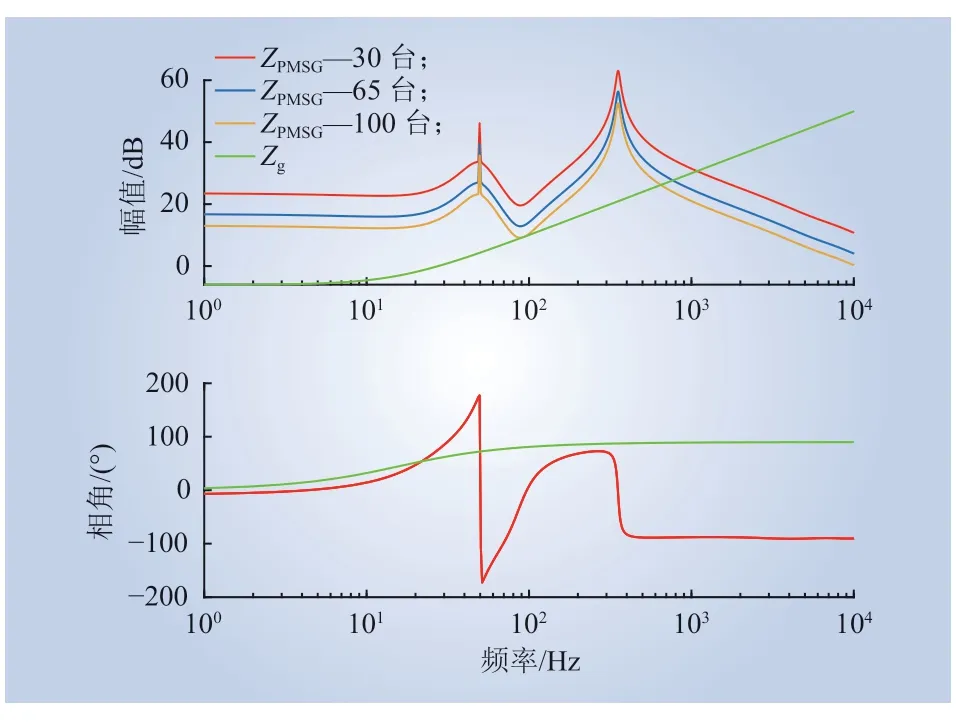
图3 PMSG 和交流系统的阻抗特性Fig. 3 Impedance characteristics of PMSG and AC system

上述是基于单台PMSG 以额定功率送出时，对直驱风电场的阻抗特性和振荡风险的分析。以下将分析PMSG 单机出力变化对其阻抗特性的影响。

图4 为直驱风电场100 台风机并网时，PMSG单机有功功率变化时的阻抗特性曲线，红色、蓝色、黄色、紫色曲线分别代表PMSG 单机出力为1.00 p.u.、0.75 p.u.、0.50 p.u.、0.25 p.u.时的阻抗特性曲线。由图4 可知，PMSG 单机出力变化时对直驱风电场的阻抗特性影响主要体现在工频附近，对中、高频段阻抗特性影响很小。

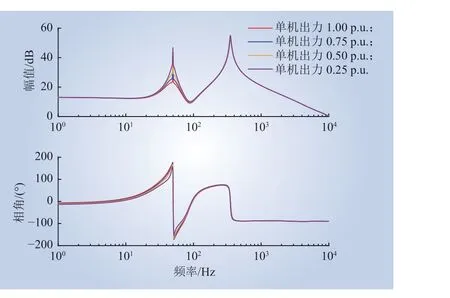
图4 单机有功功率变化时PMSG 的阻抗特性Fig. 4 Impedance characteristics of PMSG when the active power of a single PMSG changes

图5 为无功功率变化时PMSG 的阻抗特性，蓝色、黄色、紫色曲线分别代表PMSG 单机无功功率为0、1 p.u.、-1 p.u.时的阻抗特性曲线。由图5 可知，无功功率控制仅会对低频段(100 Hz 以下)造成一定影响，中高频段的阻抗特性没有出现明显变化。因此，PMSG 网侧变流器吸收或发出无功均不会造成中高频谐振频率的改变。

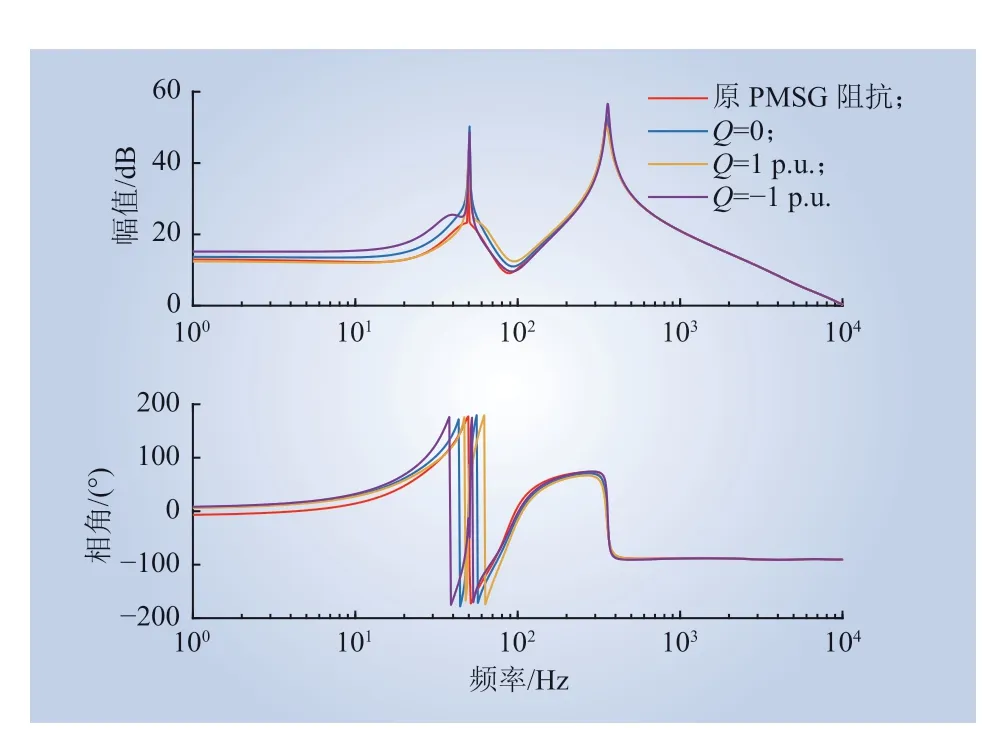
图5 单机无功功率变化时PMSG 的阻抗特性Fig. 5 Impedance characteristics of PMSG when the reactive power of a single PMSG changes

上述分析表明，当风电场并网台数增加时，系统谐振频率会降低；反之，系统谐振频率将升高。而PMSG 单机有功功率和无功功率的变化对风电场阻抗特性的中、高频段几乎无影响。因此，在系统参数不变的情况下，谐振频率主要取决于风电场并网的台数。

3 基于加窗FFT 的附加QPR 控制器设计

3.1 控制器整体设计

基于加窗插值FFT 频率检测的附加QPR 控制器的主要设计思路如下。

（2）对电气量加窗，并将加窗后的结果送入FFT 中，可以得到幅值和相角。

（3）利用所加窗函数对应的修正公式[19]对得到的幅值量进行修正，最后筛选出振荡频率，反馈给QPR 控制器。

图7 为当KR=2、KP变化时PMSG 的阻抗特性，由图7 可知，附加QPR 后会增加新的阻抗幅值交点，当KP增大时，右侧新的阻抗幅值交点处对应的相位差减小，相位裕度增大，系统不易发生振荡。反之，当KP减小时，由于相位裕度减小，系统可能将产生新的谐振点。

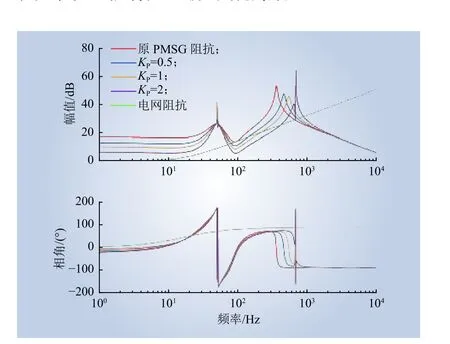
图7 K R = 2、 KP变化时PMSG 的阻抗特性Fig. 7 Impedance characteristics of PMSG when K R = 2 and KP changes

3.2 QPR 控制器参数设计

QPR 控制器可实现对正弦交流量的无静差跟踪。通过QPR 控制器，将振荡分量控制为0，从而实现振荡的抑制。图6 中带阻滤波器和QPR 控制器传递函数表达式分别为

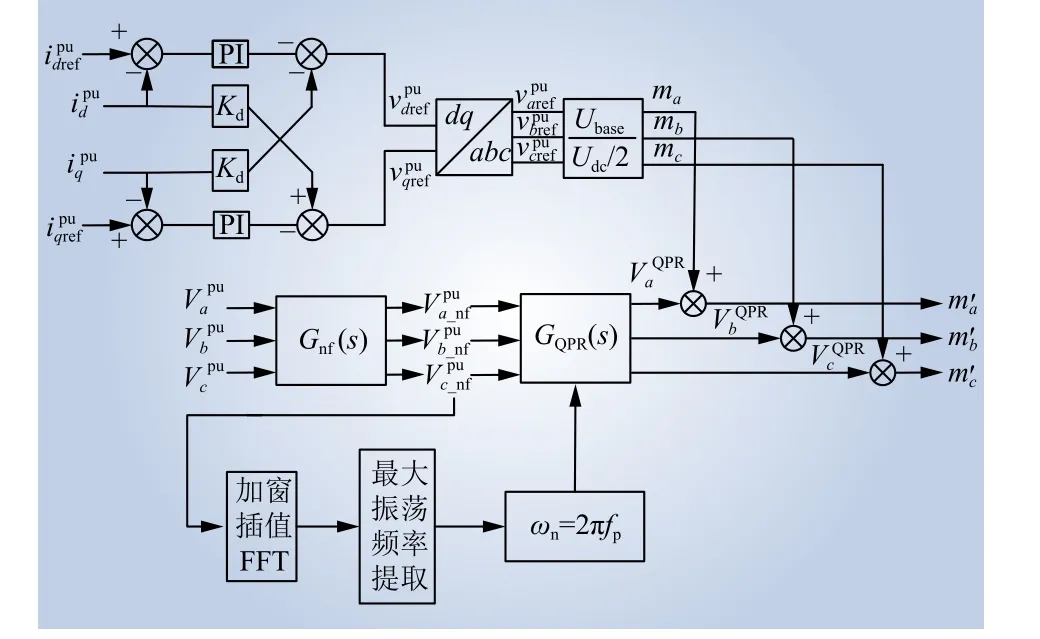
图6 基于加窗FFT 的附加QPR 整体控制框图Fig. 6 Overall control block diagram of additional QPR based on windowed FFT

图8 为当KP=2、KR变化时PMSG 的阻抗特性。由图8 可知，当KR增大时，右侧新的阻抗幅值交点处对应的相位差会增大，可能会导致相位裕度不足，造成出现新谐振点的可能性。

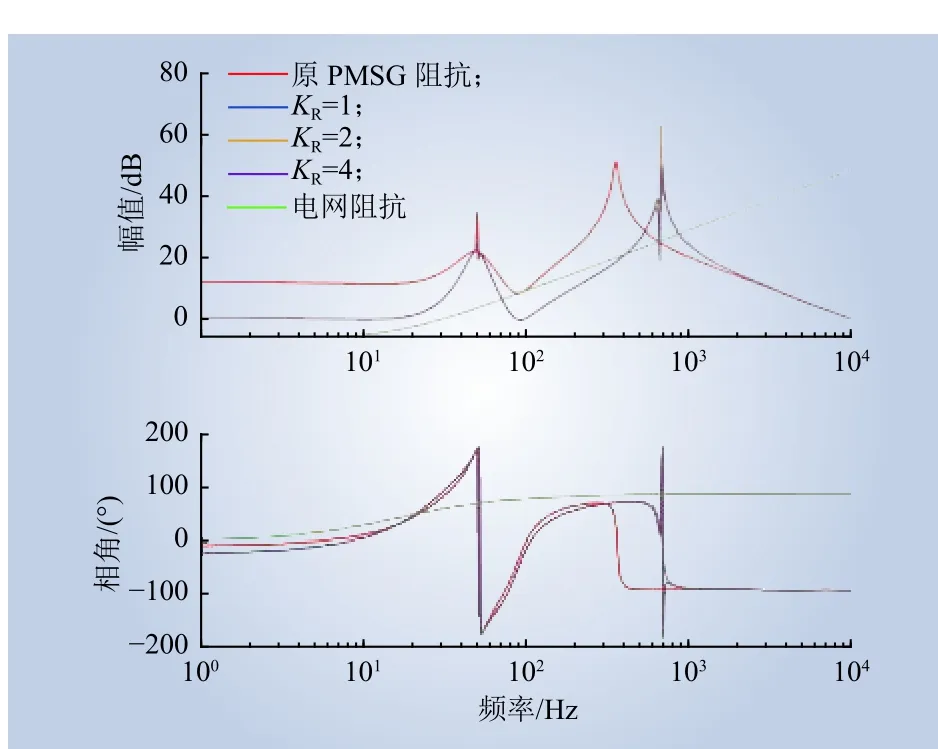
图8 KP= 2、 KR变化时PMSG 的阻抗特性Fig. 8 Impedance characteristics of PMSG when KP= 2 and K R changes

根据阻抗特性分析，当增大KP、减小KR时，可以提高并网系统的稳定裕度。另外，考虑到KP决定系统对阶跃信号的瞬态响应速度，KR决定系统对基波信号的响应速度。KP、KR越大，系统稳态误差越小，但同时系统的稳定性会减弱[23]。因此，在设计QPR 控制器的KP和KR时，需要综合阻抗特性以及仿真结果分析，既要避免出现新的谐振点，又要考虑到系统的动态性能。

3.3 基于加窗FFT 的频率检测方法

在系统实际运行过程中，振荡的频率会受到电网运行方式、风机并网台数等因素影响而产生较大的变动。利用附加QPR 控制器来抑制振荡需要提前获取振荡频率来设计合适的参数，否则可能会造成抑制效果变差或产生新的谐振点。为实现控制器能随振荡频率改变而自动调整参数的功能，需要设置振荡频率的自动检测环节。FFT 作为可以快速简便地辨识频率的工具已被广泛使用。但传统基于矩形窗的FFT 在截取时间较短的情况下，栅栏效应会导致频率辨识不准确。为提高频率辨识的准确度，本文采用加窗插值算法。

3.3.1 加窗插值FFT 频率检测的设计

对FFT 加窗函数并插值修正，可以使FFT 的检测精确度大幅提高。该方法的实质是通过插值来增加FFT 谱线数，减少谱线的间隔，从而提高检测精度。图6 中最大振荡分量提取算法流程如图9 所示。

图9 中的算法流程可以表述为：将加窗FFT计算出的频谱幅值做如下判断，若该幅值大于设定的阈值并且为极大值，便将其提取作为备选振荡频率fp′(i)；若不满足判别条件，则对下一个频谱幅值做判断。待所有频谱幅值被检测完毕后，即可得到备选振荡频率，对其修正并将修正结果滤波。根据频率检测结果，可以得到 ωn，直接反馈给控制器，控制器立刻动作，当频率检测结果稳定后， ωn维持不变。

图9 基于加窗插值FFT 的振荡频率检测算法流程Fig. 9 Flowchart of oscillation frequency detection algorithm based on windowed interpolation FFT

在频率检测和提取过程中，阈值的选取过大会导致频率检测速度降低，过小会导致频率检测结果波动较大，需要根据基波电压幅值设定，一般应满足谐波畸变率小于3%。另外，还应考虑背景谐波的干扰，应调研该地区各次背景谐波幅值，以对相关谐波设定特殊阈值。

滤波环节为一阶低通滤波器，表达式为

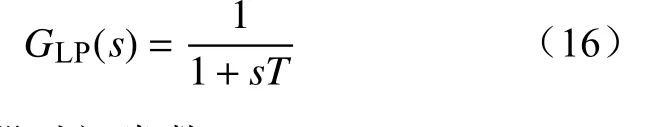
式中：T为滤波器时间常数。

由于振荡起始阶段FFT 获取数据长度不足，会产生较大频率检测误差，会导致检测出的振荡频率波形出现200～2 000 Hz 的波动。综合考虑频率检测的速度和滤波的效果，本文设置时间常数T=1 ms。

3.3.2 FFT 频率检测结果对比

为保证加窗后FFT 频率检测的效果，对比加窗函数后FFT 的检测结果与原始矩形窗FFT 的检测结果。汉宁窗的公式简便，修正效果显著，因此本文选择汉宁窗。

实际系统在振荡时会出现频率耦合现象，中心振荡频率附近会出现其他谐波，这会对频率检测造成干扰。下面构造2 个处于中心振荡频率附近的振荡频率信号，中心振荡频率为656 Hz。下面构造一个含有关于中心振荡频率对称的振荡频率信号，中心振荡频率为656 Hz，信号表达式为

采用双谱线插值算法，取截断信号数据长度N=512、1 024、2 048，采样时间ts=100 μs，采样频率为采样时间的倒数，即fs=10 kHz得到的结果如表2 所示。

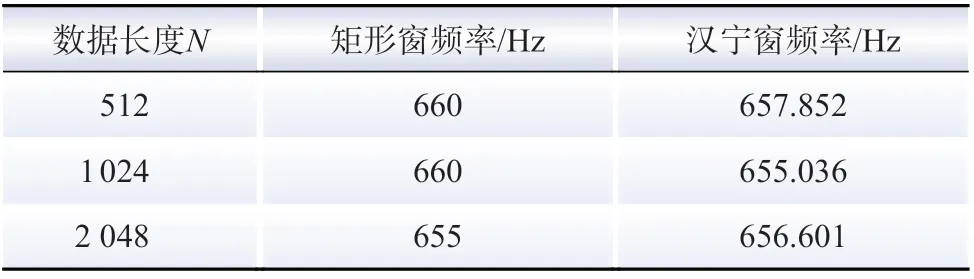
表2 矩形窗和汉宁窗频率检测结果对比Table 2 Comparison of frequency detection results between rectangular window and Hanning window

由表2 可知，在采样时间达到100 μs时，汉宁窗FFT 频率检测结果可以达到1 Hz 以内的误差，准确度较高。控制器收到频率检测结果便可以快速动作，而矩形窗频率检测结果由于栅栏效应随时间缩短误差变大。

4 仿真验证

本节基于PSCAD/EMTDC 搭建直驱风电场接入交流系统的仿真模型，复现振荡，并对比基于加窗FFT 和传统FFT 控制策略的振荡抑制效果。

4.1 振荡复现

由第2 节的理论分析得出，直驱风电场阻抗特性主要取决于PMSG 并网台数。以下将分别分析固定PMSG 单机出力、并网台数变化，固定并网台数、PMSG 单机出力变化2 种情况对振荡的影响。

（1）PMSG 单机出力为额定值，并网台数变化。

直驱风机并网在0.8 s 时解锁，之后逐渐增加风电场出力，在1.6 s 之前，风电场并网台数增加至100 台，在1.6 s 时，并网台数减少至65 台，2 s 时，并网台数继续减少至30 台。当并网台数变化时，并网点电压波形如图10 所示。

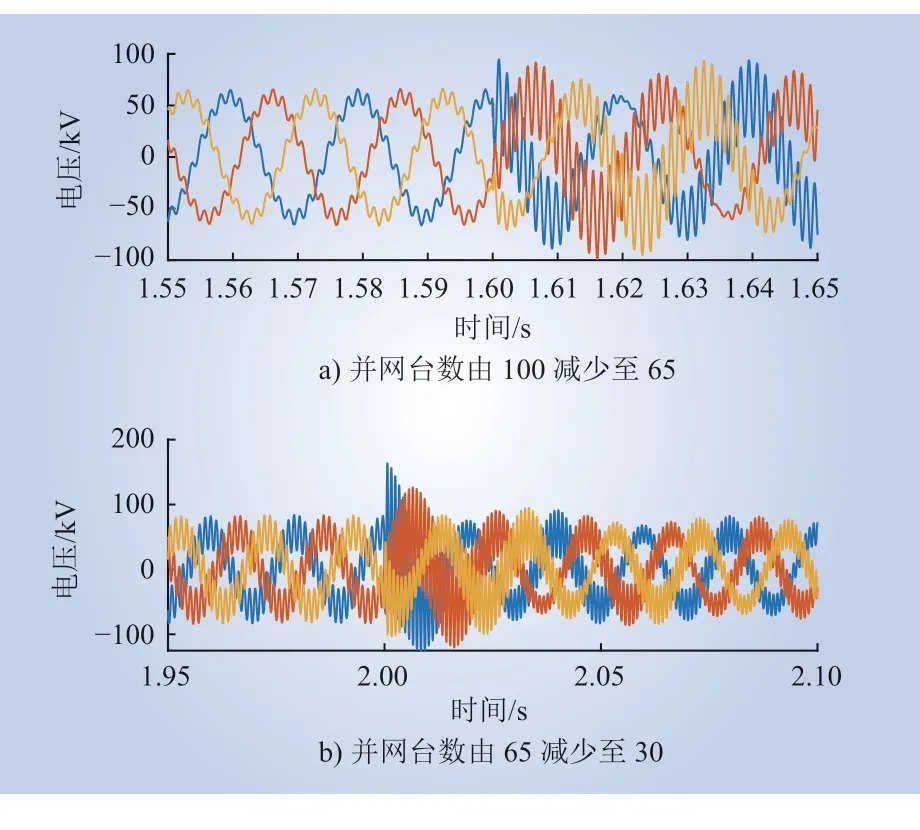
图10 PMSG 单机出力为额定值，直驱风电场并网台数减少时并网点电压波形Fig. 10 Voltage waveform of the grid-connected point when the output of a single PMSG is the rated value and the number of grid-connected PMSGs in the wind farm decreases

由图10 可知，风电场并网台数减少前并网点电压波形就出现了明显的谐波分量，主要分布在661 Hz 附近，与第2 节中理论分析结果(656 Hz)基本一致。1.6 s 时，并网台数由100 减少至65，并网点电压波形发生了明显改变，波形仍存在高频谐波分量，主要分布在780 Hz 附近，与理论分析结果(772 Hz) 基本一致。2 s 时，并网台数由65 减少至30，波形高频谐波分量继续变化，分布在1 088 Hz 附近，与理论分析结果(1 083 Hz)基本一致。

图11 为传统FFT 和加窗FFT 对风电场并网点电压最大振荡频率的检测结果。由图11 可知，2 s 时风电场并网台数减少后，加窗FFT 检测到稳定的频率时间为5 0 m s 左右，传统F F T 为100 ms 左右。即取相同的截断信号数据长度N时，加窗FFT 的频率检测速度提高了1 倍。

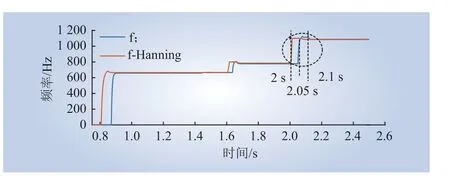
图11 传统FFT 和加窗FFT 频率检测结果Fig. 11 Frequency detection results of conventional FFT and windowed FFT

（2）并网台数不变，PMSG 单机出力变化。

图12 为PMSG 单机有功功率从额定值阶跃至0.5 p.u.时并网点电压波形。经FFT 分析可知，1.6 s后，PMSG 单机出力改变后并不会使中高频振荡频率改变，但会使振荡的幅值发生变化。图13 为PMSG 单机无功功率从0 阶跃至0.5 p.u.时并网点电压波形。同样地，PMSG 单机无功功率改变后也仅影响中高频振荡的幅值。

图13 PMSG 单机无功功率变化时并网点电压波形Fig. 13 Voltage waveform of the grid-connected point when the reactive power of a single PMSG changes

4.2 振荡抑制

为验证基于加窗FFT 的QPR 控制器抑制振荡的效果，本节选择典型比例谐振控制参数KP=1,KR=4，并设置2 种工况对比传统FFT 和加窗FFT频率检测对振荡抑制效果的影响。

（1）PMSG 单机出力为额定值，并网台数变化。

图14 为利用加窗FFT 检测频率时，直驱风电场并网台数由100 减少至65 时并网点的电压和电流波形。由图14 a) 可知，风电场出力减少后，1.63 s 谐波畸变率降低到1.98%，振荡抑制时间仅需30 ms 左右。

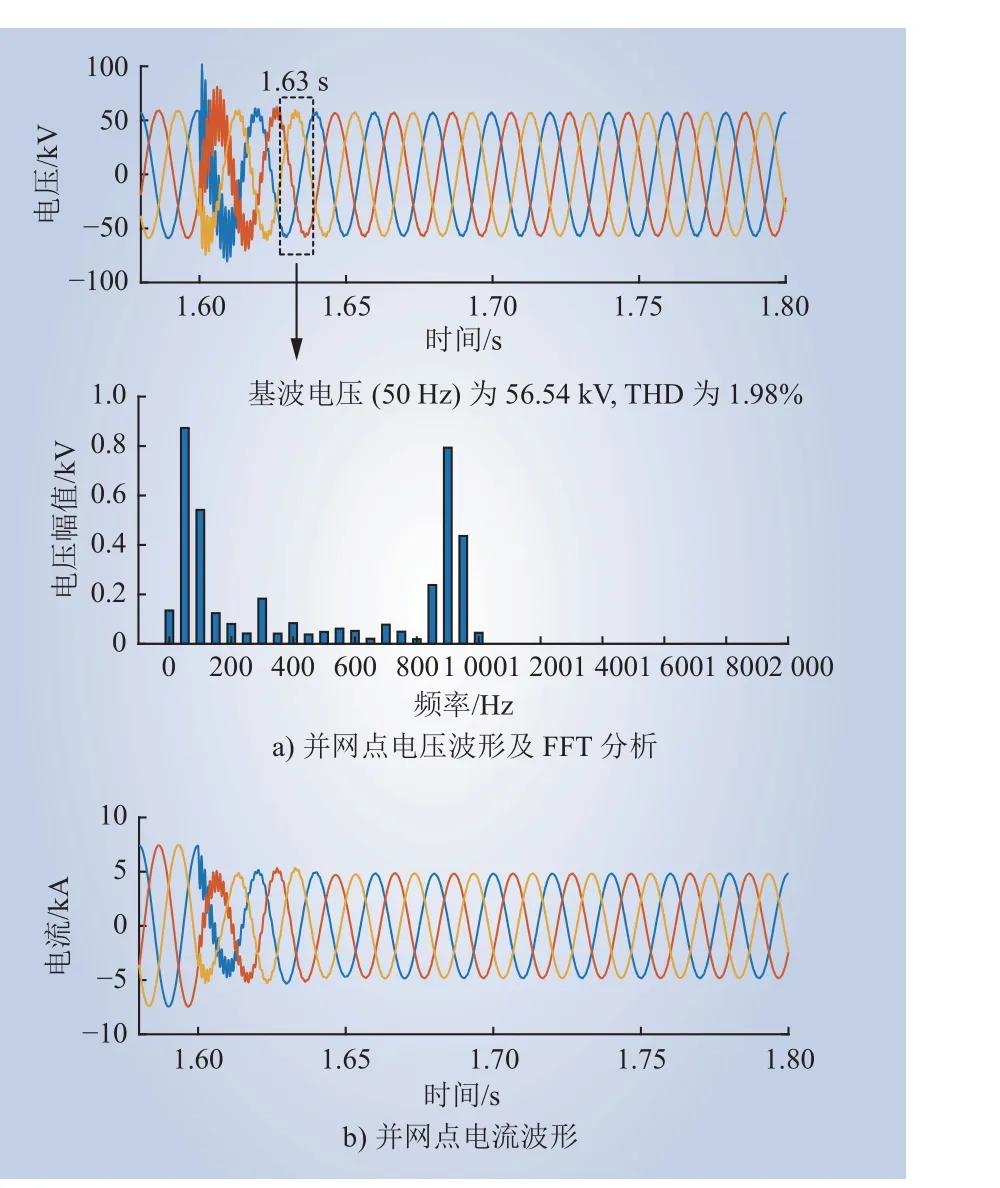
图14 直驱风电场并网台数减少后，加窗FFT 频率检测时并网点电压和电流波形(100→65)Fig. 14 Voltage and current waveforms of the gridconnected point during frequency detection with windowed FFT when the number of grid-connected PMSGs in the direct-drive wind farm decreases (100→65)

图15 为利用传统FFT 检测频率时，直驱风电场并网台数减少时并网点的电压和电流波形。由图15 a) 可知，1.75 s 时，并网点电压波形的谐波畸变率为2.96%。可见，利用加窗FFT 检测时，振荡的抑制速度提高了120 ms 以上。

由图14 b)和图15 b)可知，系统的调节时间在50 ms 左右，在阶跃响应下有良好的动态性能。可见，基于加窗FFT 频率检测的控制器可以保证系统在具有良好动态性能的情况下，并且相较于传统FFT 对振荡的抑制速度有显著提升。

图15 直驱风电场并网台数减少后，传统FFT 频率检测时并网点电压和电流波形(100→65)Fig. 15 Voltage and current waveforms of the gridconnected point during frequency detection with conventional FFT when the number of grid-connected PMSGs in the direct-drive wind farm decreases (100→65)

继续将直驱风电场并网台数由65 减少至30，对比分析基于加窗FFT 和基于传统FFT 振荡抑制策略的抑制效果。图16 为利用加窗FFT 检测频率时，直驱风电场并网台数由65 减少至30 时并网点的电压和电流波形。由图16 a)可知，风电场并网台数减少后，控制器立刻动作，2.06 s 谐波畸变率降低到2.53%，振荡抑制时间在60 ms 左右。

图17 为利用传统FFT 检测频率时，直驱风电场并网台数减少时并网点的电压和电流波形。由图17 a)可知，2.14 s 时，并网点电压波形的谐波畸变率为2.90%。可见，利用传统FFT 检测时，振荡的抑制速度降低了80 ms 左右。由图16 b)和图17 b) 可知，系统的调节时间同样在50 ms 左右，动态性能良好。

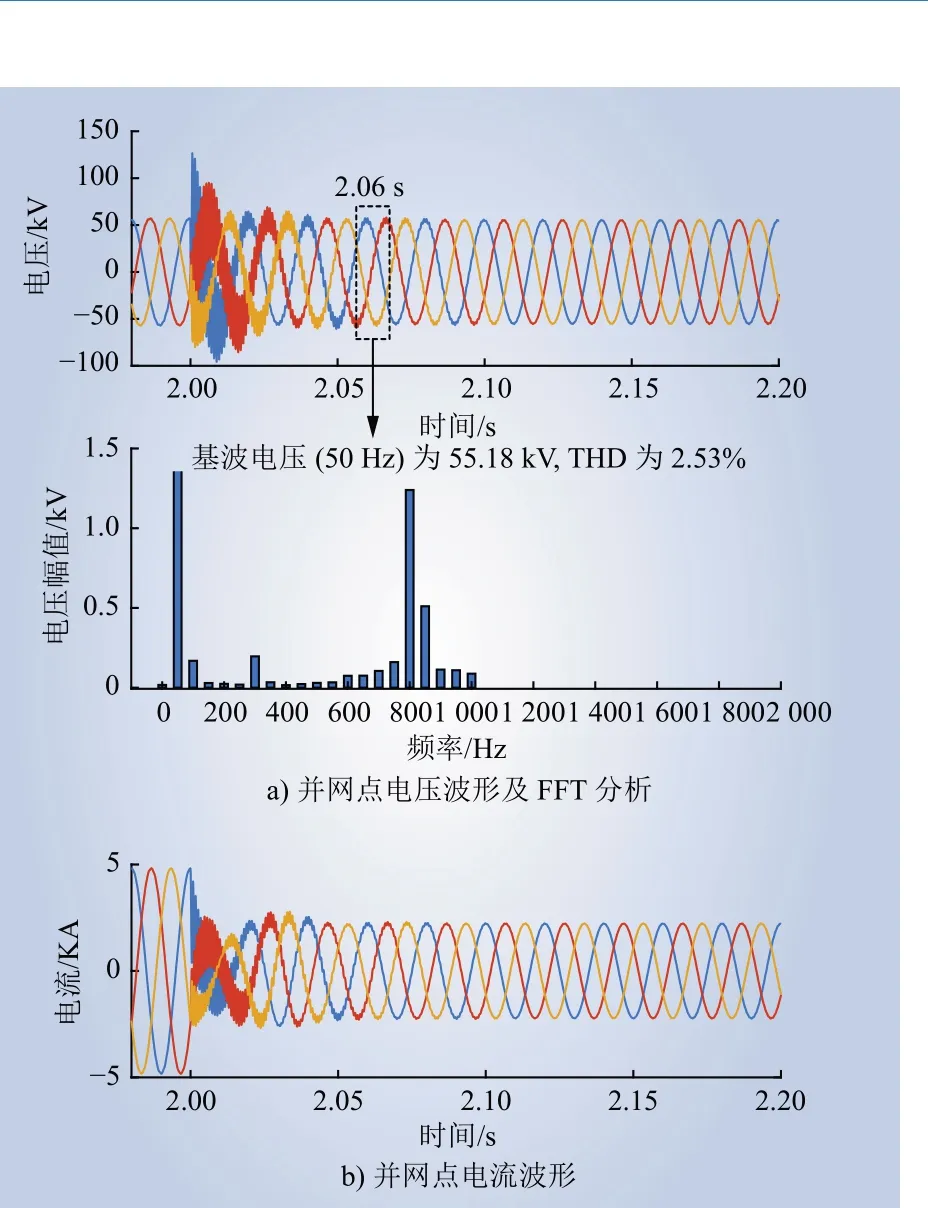
图16 直驱风电场并网台数减少后，加窗FFT 频率检测时并网点电压和电流波形(65→30)Fig. 16 Voltage and current waveforms of the gridconnected point during frequency detection with windowed FFT when the number of grid-connected PMSGs in the direct-drive wind farm decreases (65→30)

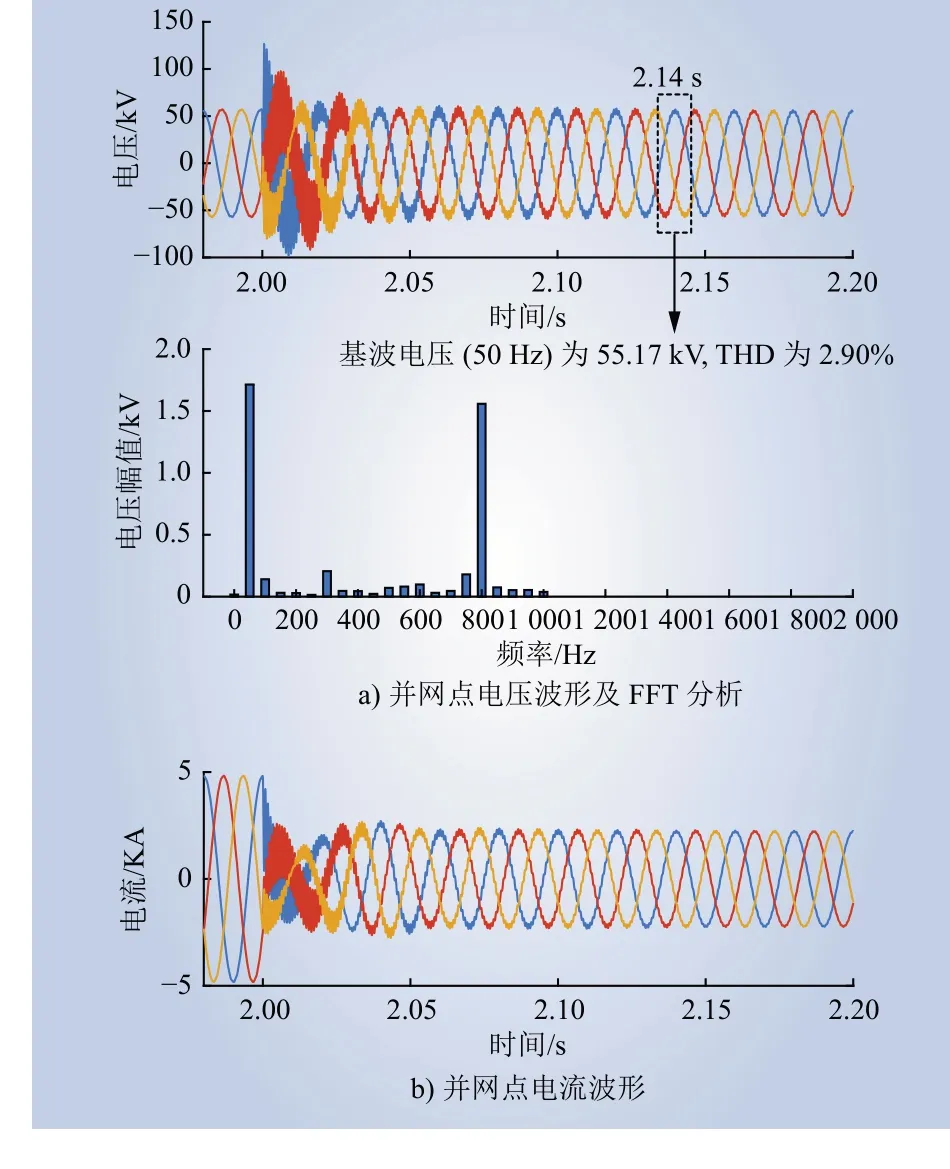
图17 直驱风电场并网台数减少后，传统FFT 频率检测时并网点电压和电流波形(65→30)Fig. 17 Voltage and current waveforms of the gridconnected point during frequency detection with conventional FFT when the number of grid-connected PMSGs in the direct-drive wind farm decreases (65→30)

（2）并网台数不变，PMSG 单机出力变化。

将PMSG 并网台数固定为100，PMSG 单机有功功率由额定值减小至1 p.u.，PMSG 单机无功功率由0 增大至0.5 p.u.，使用加窗FFT 振荡抑制策略时，并网点的电压和电流波形分别如图18 和图19 所示。

由图18 可知，1.6 s PMSG 有功功率阶跃时，系统经过约50 ms 的动态调节过程后达到稳态。图19 的无功功率阶跃波形同样仅经过一定时间的动态调节过程达到了稳态。以上分析表明，在PMSG并网台数不变，改变单台PMSG 的有功功率和无功功率时，不会产生新的振荡频率，控制器无须更新中心角频率参数，因此波形在有功、无功阶跃后也不会出现短时间的高频振荡现象，仅有短时间的动态调节过程。在该工况下，基于加窗FFT 和传统FFT 频率检测的控制策略对振荡的抑制效果无明显差别。

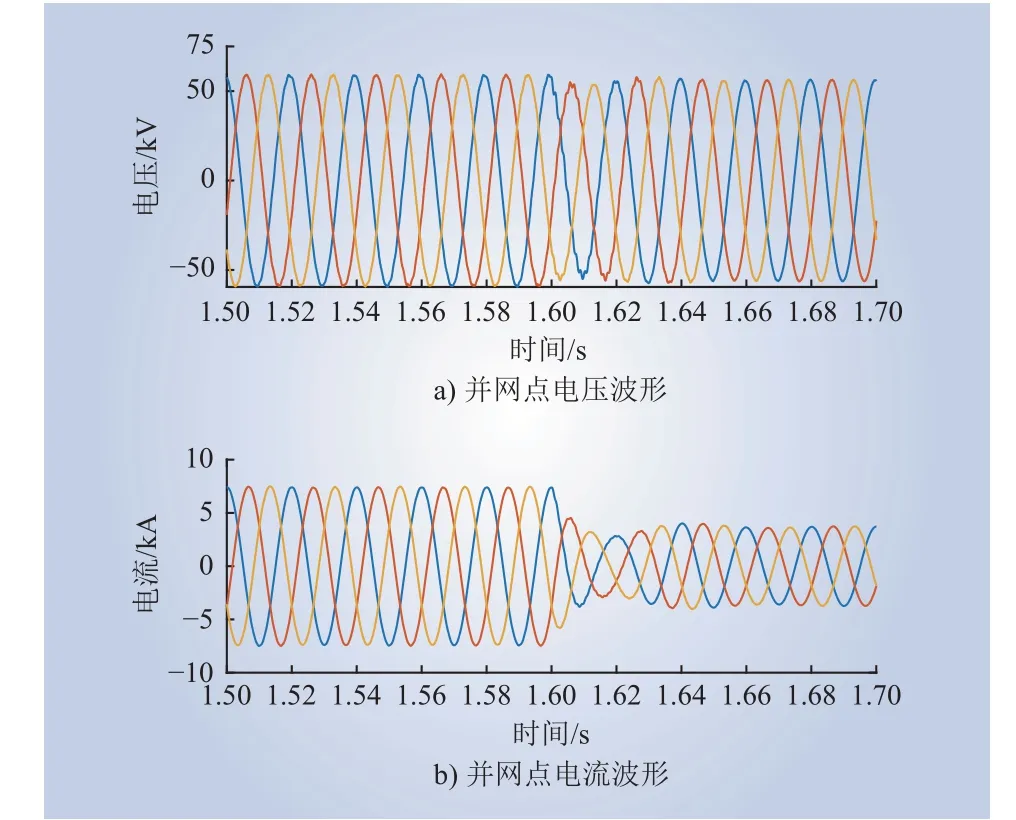
图18 PMSG 单机有功功率由额定值减小至1 p.u.时，并网点的电压和电流波形Fig. 18 Voltage and current waveforms of the gridconnected point when the active power of a single PMSG decreases from the rated value to 1 p.u.

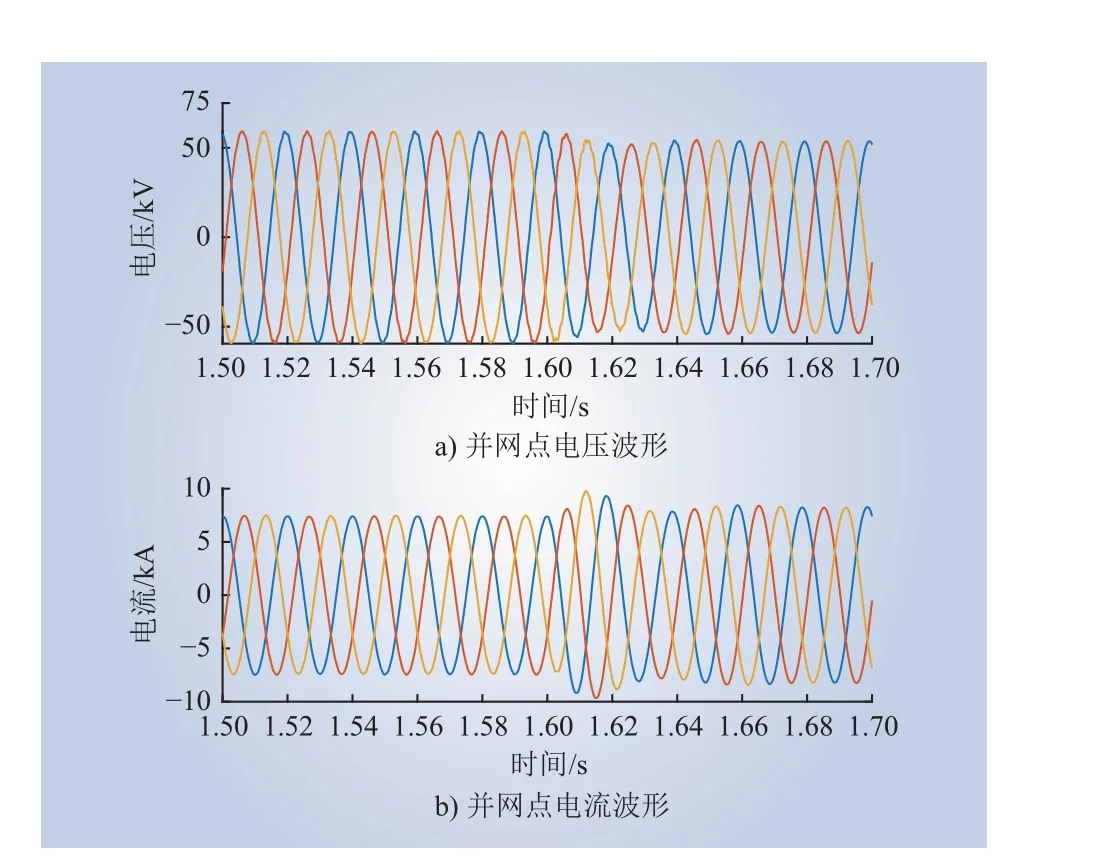
图19 PMSG 单机无功功率由0 增大至0.5 p.u.时，并网点的电压和电流波形Fig. 19 Voltage and current waveforms of the gridconnected point when the reactive power of a single PMSG increases from 0 to 0.5 p.u.

综上分析，基于加窗FFT 频率检测的振荡抑制策略可以快速抑制振荡，且系统具有良好的动态性能。同时，该抑制策略在振荡频率变化时，抑制振荡的速度上明显优于基于传统FFT 频率检测的振荡抑制策略。