航天器多约束姿态规划与控制:进展与展望综述
2022-11-05胡庆雷邵小东杨昊旸段超
胡庆雷,邵小东,杨昊旸,段超
1. 北京航空航天大学 自动化科学与电气工程学院,北京 100191 2. 北京航空航天大学 杭州创新研究院(余杭),杭州 311100 3. 北京航空航天大学 航空科学与工程学院,北京 100191
姿态控制系统作为航天器最为重要的分系统之一,是航天器实现高精度高稳定度姿态调整的保障,对空间任务的顺利实施尤为关键。航天器的姿态控制系统主要由以下4部分组成[3]:测量单元、规划单元、控制单元和执行机构,如图1所示。测量单元利用星载姿态和角速度测量敏感器(如星敏感器、速率陀螺等)实时监测航天器运动信息并反馈给规划和控制单元,规划单元则根据航天任务需求规划出任务轨迹并生成相应的控制指令,随后控制环节根据这些指令输出控制信号,通过驱动执行机构实现航天器稳定飞行或跟踪制导指令。强自主、高可靠、高精度的姿态规划与控制技术是保证航天器在复杂空间环境下稳定可靠运行并安全实施空间任务的关键。
航天器在轨执行姿态机动时往往会面临复杂的约束,本文将这些约束分为 4 大类。第 1 类为状态约束,主要包括空间指向约束和角速度约束[4-5],而且空间指向约束又细分为禁止指向约束和强制指向约束[6]。禁止指向约束源于星载光学敏感载荷(如红外望远镜、激光干涉仪等)应避免直接指向太阳、月亮等光亮目标,以防止光线影响观测[7]。例如,红外天文学卫星(Infrared Astronomical Satellite, IRAS)要求搭载的红外望远镜的指向与太阳方向的夹角不小于60°以防止光线直射,使其能够工作在红外观测所需的低温环境下。JWST、Hubble 望远镜、红外空间天文台(Infrared Space Observatory, ISO)以及 Cassini 号深空探测器也都存在类似的禁止指向约束[8]。强制指向约束的场景是承担中继通信、深空探测和编队飞行等任务的航天器需要保持天线对准地面站或邻居航天器,以稳定地维持通信链路[9]。角速度约束源于速率陀螺、星敏感器等角速度传感器的量程有限,要求航天器的角速度必须维持在特定的范围内,例如美国的 X 射线计时探测器(X-ray Timing Explorer, XTE)[10]。第 2 类为物理约束,包括执行机构输出幅值和速率约束,主要源于反作用飞轮、控制力矩陀螺等姿控执行机构的有限输出能力[11]。第 3 类为任务性能约束,包括时间和能耗约束,其中时间约束主要是由任务时间窗口造成的[12],而能耗约束则是源于航天器所携带的工质燃料有限,且其所配备的电能生产和存储设备有限[13]。规划环节需要重点考虑前述 3 类约束。第 4 类为广义约束,主要包括参数不确定性、多源干扰、执行机构故障、暂稳态性能以及测量信息不完备等,这些约束都严重影响了航天器安全、姿态控制精度及稳定度,在姿态控制器设计中需要对这些约束进行考虑,才能从稳定性和安全性角度保证航天器姿态控制系统的正常工作。综上所述,研究复杂约束下的航天器姿态规划与控制新理论与新方法,是当前航天器控制领域的前沿热点方向,已成为进一步提升航天器智能自主性、安全可靠性和任务执行能力的核心关键,具有重要的现实意义。
本文基于课题组前期研究成果,并参阅国内外知名团队和学者的部分代表性工作,总结和梳理了现有航天器多约束姿态规划与控制方法的研究思路和优缺点,并给出了未来发展建议,希望对从事相关研究的同行学者和工程人员提供一定的参考。航天器多约束姿态规划与控制技术经过20多年的发展,算法研究仍方兴未艾,尤其是结合人工智能等前沿技术的新成果近年来更是层出不穷,论文未能提及之处,敬请谅解。
1 约束分析与表征
正如引言中所分析,在航天器执行在轨任务的过程中,姿态系统面临着多种约束。在针对这些约束设计安全的规划和控制算法之前,需要首先针对这些约束进行分析并利用适当的数学表达式来刻画。本节将对状态约束、物理约束、任务性能约束以及广义约束进行分析与表征。其中前 3 类约束主要面向姿态规划算法设计,而广义约束则主要是面向姿态控制器设计。
1.1 状态约束
1.1.1 空间指向约束
在轨飞行任务中,由于星上载荷保护和通信保障等原因,航天器的姿态将受限于特定的指向空间中,这使得航天器姿态机动路径的可行空间大大减小,因此分析姿态指向约束的形成原理及其分类具有重要的实际工程指导意义。本文所考虑的指向约束可以分为 2 大类[6]:禁止指向约束和强制指向约束。
1) 禁止指向约束
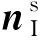
(1)
(2)
(3)
(4)
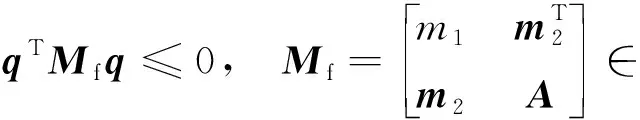
(5)
2) 强制指向约束
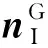
(6)
同样的,也可以用修正罗德里格斯参数和单位四元数的形式表述:
(7)
qTMfq≤0
(8)
上述对于指向约束的描述是以传感器视线场约束为圆锥体,而实际的传感器视线场约束区有可能为台体等形状,对于这一类多面体的约束在工程上也往往以其外包络圆锥(或内切圆锥)进行描述以便于实现。
本节的分类是根据约束区域的进入和逃出划分的,除此之外还可以根据约束区域的时变性分为动态指向约束和静态指向约束。而且还可根据约束所承受的严格程度分为硬约束和软约束,前者是在全过程中都要满足的约束,而后者则为时间积分约束,当其积分值小于某个指标值时不产生约束效果,当大于指标值时,该约束转变为硬约束。在一些复杂的任务场景中,上述2种约束可能同时存在,且往往是动静、软硬并存的,这种更为复杂的约束情况会给航天器的规划与控制系统带来了更大的挑战。
1.1.2 角速度约束
以光纤陀螺为代表的角速度测量仪器,往往存在着测量范围的限制[10],因此需要保证航天器的角速度ω=[ω1,ω2,ω3]T∈3的3个分量都需要在量程范围ωR内,数学表示为
|ωi|≤ωRi=1,2,3
(9)
对于以星敏感器为代表的姿态测量仪器在轨工作时需要保证整体的转动角速率不能过大以保证光学测量系统能正常捕获定位,同时也考虑到航天器本身的部件结构强度在转动过程中不会被甩出,因此在姿态机动的过程中的角速度必须保持在星体可承受的上限ωM内[15]。这类角速度约束可以由如下不等式描述:
(10)
1.2 物理约束
1) 执行机构幅值饱和
航天器姿态控制系统常见的执行机构主要包括:推力器、反作用飞轮、控制力矩陀螺、磁力矩器等[16]。尽管这些执行机构的工作原理有所不同,但它们的输出幅值均受限。鉴于此,在姿态规划和控制算法设计时,控制输入τ∈N(N为执行机构的数量)需要满足如下约束:
|τi|≤τMi=1,2,…,N
(11)
式中:τM>0为幅值限制。
2) 执行机构速率饱和
除了输出幅值限制,由于执行机构自身响应机理等原因,其输出力矩的变化率也受限,具体可描述为如下不等式[11]:
(12)
式中:sM>0为速率幅值限制。
1.3 任务性能约束
对于某些航天器姿态机动任务,机动时间和能量消耗是重要的任务性能指标,为规划算法的设计引入了相应的约束。
1.3.1 任务时间约束
考虑到一些在轨观测任务(如重要目标的侦察等),其存在最佳的观测窗口[12],需要在最佳观测窗口开始之前使航天器机动到特定的指向范围内,可以描述为如下时间约束:
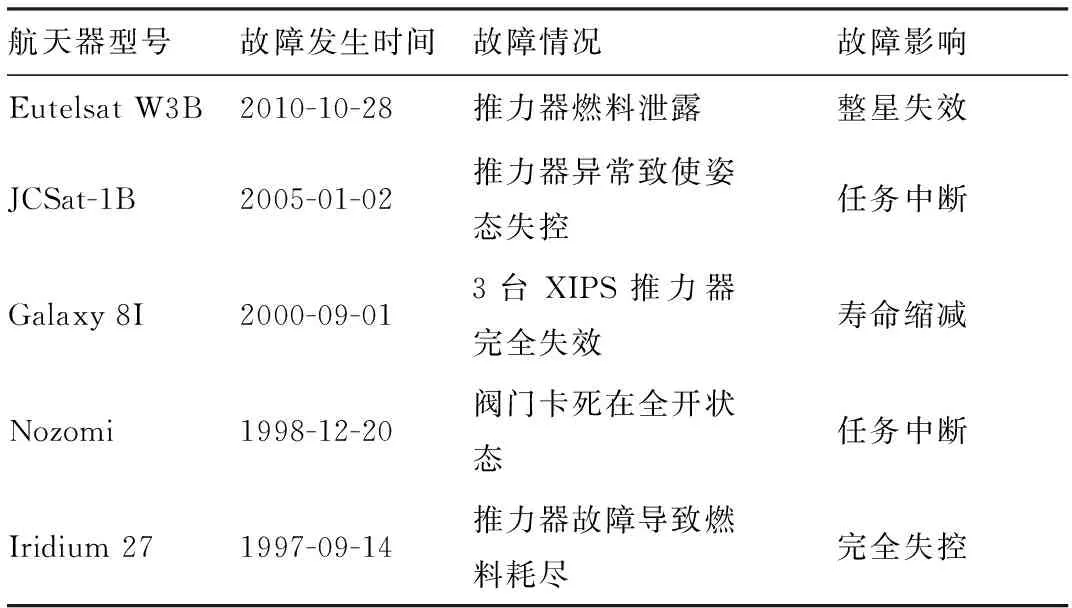
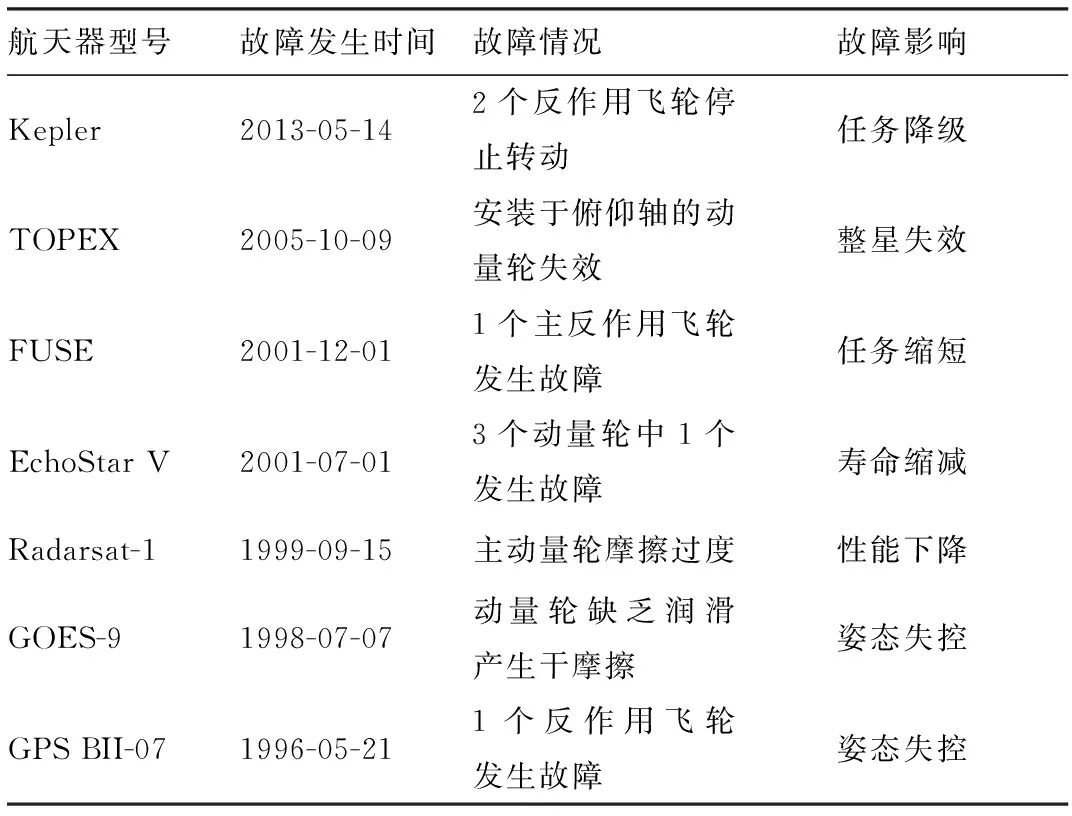
0 (13) 式中:Tf为姿态机动过程所用时间;Tw为当前时间距离任务最佳观测窗口开始的时间。 1.3.2 能量消耗约束 在轨航天器不仅所携带的工质燃料不多,其所配备的电能生产和存储设备也是有限的。因此在姿态机动过程中执行机构所消耗的燃料也会受到限制。 对于使用推力装置的航天器而言,其能量消耗以工质燃料的质量减少来计算,其过程可表示为[17] (14) 式中:mF为最大工质燃料消耗质量限制;fk为每个推力器产生的推力;NT为推力器的数量;Isp为推力器的比冲系数;g0为重力系数。 对于使用电机作为动量交换装置进行姿态机动的任务而言,其能量消耗以电机消耗的能量来计算,其过程可表示为[13] (15) 式中:E为本次任务可消耗的最大电能;Nτ为电机的数量;Pi为每个电机的瞬时功率,可以由如式(16)计算: (16) 其中:τi为每个电机的输出力矩;Ωi为每个电机的转速;KT、Rm、βm分别表示电机的扭矩系数、电枢电阻、黏滞摩擦系数。 在姿态机动任务中,往往不是由单一种类执行机构实现的,在考虑混合执行机构的能量消耗时,可综合考虑式(14)和式(15)来处理。 上述2点阐述的性能约束主要是考虑时间或者能耗小于一个确切的值。但是,在大多数姿态控制系统的设计中,往往将它们作为优化的性能指标综合处理。在数学上可以表示为如下的性能指标最优: (17) 式中:Q(e)为关于状态误差e的代价函数;R(u)为关于控制输入u的代价函数。前者在物理意义上即对应为任务完成时间的指标,后者则对应能量消耗的代价。在姿态控制系统设计中,通过调节两者的权重大小,即可根据实际的任务需求调整性能指标。 将参数不确定性、多源干扰、执行机构故障、暂稳态性能约束、测量信息不完备等归结为广义约束。这些约束主要影响轨迹规划后的跟踪控制器设计。下面将对各类广义约束进行简要介绍和数学描述。 1.4.1 参数不确定性 航天器在轨运行期间,载荷运动、工质及燃料消耗、目标抓捕等因素不可避免地会导致惯量参数存在不确定性。对于时变的惯量参数,可以将其写成如下形式[18]: J=J0+ΔJ (18) 式中:J0∈3×3为名义的惯量矩阵;ΔJ∈3×3为惯量矩阵的不确定部分。针对这一情况,通常可将姿态动力学中的ΔJ相关项集总到系统干扰中,并应用抗干扰控制方法对其进行处理。对于不变/慢变的惯量参数,可将动力学方程中关于J的函数项进行如下仿射线性化处理: Jx=L(x)θ∀x∈3 (19) 其中:θ=[J11,J22,J33,J12,J13,J23]T代表未知参数向量;L(x):3→3×6为已知的回归矩阵。针对线性回归式(19),可设计自适应律对未知参数θ进行在线估计[19]。 1.4.2 多源干扰 航天器在轨运行不可避免地会受到外部环境干扰力矩(包括重力梯度力矩、太阳光压和辐射力矩、气动力矩、地磁力矩等)以及内部非环境干扰力矩(包括系统建模误差、执行机构安装偏差、挠性部件振动等)的影响,这些内外部干扰力矩形成了多源异质的干扰因素,极大地影响了航天器姿态控制的精度及稳定度。文献[20] 详细分析了各类环境干扰力矩的特性以及对航天器姿态的影响,并提供了相应的数学模型,这里不再赘述。对于系统建模误差、执行机构安装偏差等内部扰动,一般对它们不进行精细化建模,而将它们视为外部干扰。这里重点描述挠性部件振动。考虑挠性航天器的动力学方程[21]: (20) (21) 式中:ω∈3为航天器的角速度;J∈3×3为航天器的惯量矩阵;τ∈3和τd∈3为控制和干扰力矩;η∈n为模态向量;δ∈n×3为耦合矩阵;D=diag{2ξ1w1,2ξ2w2,…,2ξnwn}和分别代表阻尼和刚性矩阵,ξi∈和wi∈(i=1,2,…,n)分别为阻尼比和模态频率。 需要指出的是,为便于设计现有抗干扰控制方法大多将内外多源干扰以及第1.4.3节提到的加性偏差故障归结为总干扰,并加以处理。 1.4.3 执行机构故障 航天器长时间运行在高低温、强辐射的恶劣太空环境中,执行机构(如推力器、反作用飞轮等)因需要频繁工作,极易发生故障。执行机构故障轻则导致姿态控制性能下降,重则造成系统失稳。通过分析故障对姿态控制系统的影响,可将执行机构故障分为以下4类[22]: 1) 控制输出减小:由于电气、机械等原因导致执行机构的实际输出力矩小于控制指令。 2) 输出力矩偏移:由于执行机构的结构原因和外部不确定性,其实际输出力矩在指令控制的基础上产生了附加偏移力矩。 3) 执行机构卡死:由于执行机构部件损坏或部分失效(如:喷气推力装置的节流阀泄漏等情况),导致其输出为某一不为零的常值。 4) 对控制信号无响应:由于电路、电源失效或机械结构损毁,导致执行机构不能响应控制指令,实际的输出为零。 为对1)~4)类故障进行建模,可将执行机构的实际输出力矩改写为如下形式: τ=Euc+ud (22) 式中:E=diag{e1,e2,…,eN}(0≤ei≤1)代表故障因子矩阵;uc∈N为控制力矩指令;ud∈N为加性偏差故障。 1.4.4 暂稳态性能约束 深空探测、在轨服务与维护以及空间对抗等新一代航天任务对航天器姿态控制提出了更高的性能要求,主要体现在以下几个方面: 1) 完成时间:由于任务时间紧,要求航天器在规定时间内完成给定的姿态机动任务,即ts≤T,其中ts表示系统的稳定时间,T>0为规定的任务时间。典型的例子是非合作目标在轨捕获要求在服务航天器进入阴影区前完成,否则视觉传感器将无法为捕获操作提供相对导航信息。 2) 最大超调:超调量是衡量系统动态性能的重要指标,姿态控制的最大超调一般不能超过规定的值,即(xmax-x∞)/x∞≤om,其中xmax代表瞬时最大偏差值,x∞代表输出稳态值,om为最大可允许的超调量。例如,航天器在对满足禁止指向约束的姿态轨迹进行跟踪的过程中,为避免光学敏感器的视线轴进入禁止区域,要求跟踪误差无超调。 3) 稳态误差:稳态误差是衡量控制系统稳态性能的重要指标,为了确保航天器高品质地完成指定任务,要求姿态和角速度收敛到期望值附近的可接受范围内,即稳态误差界,数学上可描述为ess≤em,其中ess代表稳态误差,em为稳态误差上界。通常,稳态误差界可根据星载敏感器的测量精度来设定。 上述性能要求对姿态控制系统施加了严格的暂稳态性能约束。 1.4.5 测量信息不完备 对于一些小型航天器(如立方卫星、微纳卫星等),由于所能容纳的载荷成本、体积、重量和功率有限,往往没有安装能够直接测量角速度的敏感元件,因此对于控制系统设计来说,得到的状态反馈只有姿态信息。上述的测量信息受限的问题可以由如下测量方程表述: y=Hx+w (23) 式中:y∈m为测量信息;H∈m×(m+3)为测量矩阵;x∈m+3表示由姿态和角速度整合的运动状态向量,当姿态由四元数表示时m=4,由 MRPs 或者欧拉角表示时m=3;w∈m为传感器测量中引入的干扰噪声。需要指出的是,对于控制器而言,其接收到的反馈信号为m维,小于被控状态的(m+3)维。 为满足深空探测、在轨服务等新型航天任务日益提升的需求,航天器需要搭载越来越多的高精度载荷与设备。为此,姿态规划算法设计不但需要考虑既定的任务目标与任务性能约束,还应当兼顾在任务执行过程中由载荷、执行机构等设备引入的各种状态和物理约束。例如,ISO 卫星设计了使载荷规避地球热辐射源的机动策略,避免对探测结果造成影响[23];Cassini 号深空探测器要求具备姿态规避机制以保护配置的传感器受到太阳照射[24];太阳能电池阵列需指向太阳,保证电力供应;XTE 卫星要求机动速度不超过速度陀螺仪的测量上限等。因此,研究多约束自主姿态规划方法,使航天器的姿态能够沿着一条满足约束的轨迹运动,尽可能地避免对设备载荷的损伤,从而有效地延长航天器寿命,是一项亟需解决的关键技术。 现有的多约束自主规划方法可大致分为几何方法、基于势函数的方法、空间离散化方法、随机采样方法、基于优化的方法与智能规划方法6类。这些方法能够处理的约束类型、轨迹寻优能力、以及计算复杂度有所不同,表1 简要总结了 6 种方法对指向约束、角速度约束与执行机构饱和的处理能力。图4 给出了方法关于寻优能力与计算复杂度的递进关系,本文也将着重在这些方面对现有多约束规划方法进行分析。 表1 不同规划方法约束处理能力对比Table 1 Comparison of constraint-handling capability of different planning methods 通过建立敏感器视线指向与特定指向之间的几何关系,传统几何方法能够有效应对姿态指向约束。一般来说,传统几何方法首先在无约束环境下,设计一种能够准确驱动航天器从起点到期望姿态的最优控制策略,而后在空间内寻找一个中间姿态,使得无约束的控制策略能够直接应用于两段路径,并且不违反任何的约束。几何方法设计简单,且能够获得解析的姿态规划策略,在计算效率上具有显著的优势。 针对太阳、异常和磁层粒子探测器 (Solar, Anomalous, and Magnetospheric Particle Explorer, SAMPEX),Frakes等[25]研究了探测器规避星体速度方向的方法,降低了空间碎片与微流星体对微粒子探测精度的影响。同时,考虑对明亮天体规避与对地通讯保持约束,Hablani[9]提出了2种替代最小旋转路径的机动方案,使得视线轴能够相切地通过禁止区,并基于其中一种方案进一步设计了天线指向策略。针对欠驱动航天器,文献[26-27] 利用非标准欧拉轴角参数,将欠驱动约束描述可行驱动轴与欠驱动轴的垂直几何关系;进一步提出了两种两步相切姿态机动策略,实现了视线轴对某个指向约束区域的规避。针对空间内多个锥形约束,徐瑞等[28]提出了有效路径约束的检测方法;通过将有效三维指向约束投影到二维平面,导出了满足约束的中间姿态的解析解。考虑太阳规避约束,Ayoubi 和 Hsin[7]提出了一种新型最优几何规划策略。 意大利Biggs团队针对连续时间系统的几何最优控制问题,取得了一系列重要成果[31-33]。Biggs 和 Colley[31]提出了一种基于特殊正交群(Special Orthogonal group, SO(3))的半解析最优规划策略,通过优化权重因子与控制参数,可实现对系统轨迹和控制幅值的限制。利用ε截面曲率的连通曲面的标架丛,Henninger 和 Biggs[32]将最优规划问题转化为两点边值问题,导出了基于拉克斯对(Lax pair)的解析解。结合人工势函数方法与滑模控制,Geng等[33]提出了一种基于对偶单位群的姿态控制律,获得了滑动阶段系统轨迹的解析形式,而后通过对系统初值与控制参数的整定,可以按需地改变系统轨迹的曲率,从而实现障碍规避。 另一方面,国内外学者研究了航天器动力学系统的几何离散化方法。针对受频率约束与点约束的李群系统,Kotpalliwar 等[34]研究了离散形式的庞特里亚金原理最优条件。李益群等[35]提出了一种基于李群谱配点法的航天器姿态仿真方法。文献[36] 提出了将变分积分子与谱方法通过伽辽金方法与打靶法结合的方法,在很好地保持了系统几何结构(辛结构、李群结构等)和物理特性(动量、能量等)的同时,不降低谱方法原有的收敛速度和计算效率。 由以上的研究结果可以看出,几何规划方法能够获得解析或半解析的最优姿态机动路径,在计算效率上具有明显优势;能够很好的保守群结构与物理特性,有利于数值计算。但是,几何方法应对较多的约束时能力有限,并且能够考虑的优化指标相对单一。 势函数方法是一种处理运动学约束非常有效的方法,该方法的基本原理如图6所示。考虑目标在一个人工势场中运动,其中障碍物处于高势能处,期望位置处于最低势能处。只需根据当前位置势能的负梯度方向设计控制力,就能实现目标远离高势能的障碍区域,驱向低势能的期望平衡点。基于势函数的控制器无需提前规划完整的系统轨迹,具有良好的实时性。国内外众多学者通过构造出形式多样的势函数形成特定的人工势场,来实现不同系统动态性能。目前,常见的势函数有指数函数(包括高斯函数)、二次型函数、对数函数、导航函数等。 针对空间光亮天体指向,Mclnnes[37]采用无歧义的高斯函数建立障碍高势能区域,结合转动动能与姿态势能的 Lyapunov 函数,提出了一种有界的姿态控制策略。Wisniewski和Kulczycki[38]基于四元数建立了哈密顿形式的姿态动力学方程,通过能量成型方法设计控制律,使得敏感指向为势能高点,期望平衡点为唯一的势能极小值点。针对航天器姿态规避问题,郑重等[39]提出一种新型的高斯势函数,保证了控制律的连续与有界。郭延宁等[40]提出了排斥势函数存在的条件,避免了不必要的退绕问题;进一步针对控制受限,设计了自适应的反步跟踪控制器,实现了控制幅值的在线自动调整。考虑多个空间内禁止区域与强制区域,美国 University of Washington 的 Lee 和 Mesbaihi[6,41]提出了一系列基于对数函数的势函数方法,实现了控制律光滑性与近似全局收敛性,进而保证了多约束求解的可行性与稳定性。崔祜涛和程小军[42]考虑了输入饱和与常值干扰下的姿态规避控制问题,利用导航函数避免了势函数方法局部极小的问题,并采用辅助系统解决了输入饱和的问题。 此外,势函数方法还能够方便地处理角速度受限约束。针对静止到静止的航天器姿态机动问题,Shen等[43]利用滑模面变量设计了一种对数型势函数,使得系统在临近角速度限制边界时具有极高的势能。笔者团队[4,44]分别考虑减小阶姿态系统与不确定姿态系统,通过设计角速度的对数势函数,实现了角速度约束。 笔者团队基于势函数方法解决了航天器姿态机动与近距离交会的问题。针对交会对接问题,Dong等[45]利用对偶四元数参数,设计了基于一种新型势函数的姿轨控制律,能够同时满足视场约束与对接走廊约束。考虑多个姿态禁止约束,笔者团队[14,46]提出了几种基于对数型势函数的姿态机动控制策略,克服了四元数的退绕问题;还针对航天器姿态机动问题,基于导航函数设计了系统的势能函数,在避免将禁止约束转化为凸约束的前提下,严格证明了势函数的极小值点能够无线趋近于系统的平衡点[47-48]。 从以上分析可以看到,势函数方法能够有效处理多类型姿态约束,且不依赖于全局信息,可以实现动态的规划。此外,势函数方法能够直接用于解析控制律设计,在计算实时性上具有明显的优势。然而,势函数方法通常会存在局部极小值问题,导致系统驻留在极小值点,不能实现既定的控制目标。 相比于前述方法共有的解析特征,下面主要介绍一系列数值优化方法,它们对多种优化指标具有更强的轨迹优化能力,为多约束运动规划问题求解提供了新思路。首先介绍一种离散化方法。这种方法利用多面体(比如立方体、二十面体)均匀离散化姿态单位球,将指向向量转换为整数,建立起指向向量的拓扑结构;通过路径规划算法将约束集转化为单位球上的像素点集;最后,定义一个关于路径长度的代价函数,利用路径搜索算法获得最(次)优路径,这一过程如图7所示。当得到期望的路径之后,就形成了描述旋转序列的一系列姿态,可以进一步通过反馈控制器来实现期望的轨迹。 目前,姿态单位球离散化的方法主要包括天立方算法(Cosmic Background Explorer,COBE)[49]、正二十面体算法[50-52]等。在 COBE 天立方算法的基础上,Tegmark[50]提出了一种基于正二十面体的离散化方法。该方法相比于COBE天立方算法具有2方面优势:①用六边形像素替代COBE天立方算法里的正方形像素,空间离散化需要更少的像素;②每个像素点有6个相似等距的邻居,使得生成的轨迹更加光滑。针对 Bevo-2 或 ARMADILLO 立方星所携带的低等级光学仪器对强光的敏感,Kjellgerg和Lightsey[51-52]基于正二十面体离散化算法提出了满足姿态指向约束与控制约束的路径规划方法。该方法将连续点离散为姿态单位球内接二十面体的正六边形像素点,并采用 A*图搜索算法搜寻可行路径。但是该方法只能考虑单一敏感设备,缺乏多敏感设备轨迹规划能力。针对这一问题,Tanygin[53-54]提出了 ARPs (Airy-Rodrigues Parameters)的定义以及一种新型最小形变投影,在新的参数下描述姿态约束并进行离散化,通过改进的 A*算法,实现了多路姿态的最优路径规划。 离散化方法具有明确的物理含义,在机器人运动规划领域也得到了广泛的应用。离散化方法能够有效地处理姿态指向约束与控制约束,实现概率意义下的最短机动路径。但是,离散化方法也具有明显的缺点,一方面是依赖于离线求解的结构,另一方面是相比于解析的方法(几何方法与势函数方法),离散化方法的计算量较大,故而难以实现动态规划,限制了其应用。 2.3节中基于空间离散化的规划方法更适用于低维度空间上的路径规划问题,它在这类问题中往往具有较好的完备性,而且需要对环境进行完整的建模,并且在高维度空间中很容易导致现“维数灾难”。为了解决这些问题,基于随机采样的规划算法被提出来[55],这一方法以概率完备性来代替完备性,从而提高搜索效率,适用于高维度空间的规划问题。这一类方法的主要原理是在可行的空间中随机生成状态点,然后找到一组可行的连通方式将这些状态点连接得到一条规划轨迹[56],具体过程如图8中所示。 利用随机规划算法的原理,许多学者也开展了航天器姿态机动规划研究。美国麻省理工大学的Feron等[57]提出了一种基于快速扩展随机树(Rapidly exploring Random Tree, RRT)的随机姿态规划方法,并基于 Lyapunov 函数建立局部制导律,在多种类型的姿态约束下,实现了航天器大角度姿态指向路径规划。Yershova 和 Lavalle[58]提出了在旋转矩阵空间上的确定性采样算法,这种分辨率完备性的采样方式为姿态随机规划算法的发展提出了崭新的方向。利用确定性采样方法来更换传统 RRT 算法中的完全随机采样方法,可以在一定程度上减少 RRT 算法所用时间。文献[59-60] 将姿态描述从旋转矩阵映射到罗德里格参数中进行姿态指向规划,减小了变量维度、提高了规划速度,但也造成了某些工况下的搜索范围扩大。 采用基于随机算法的规划方法的优点是能够解决各种类型的运动轨迹约束,利用基于概率的方法提高了计算效率。但是,正是因为采用了随机概率的机制,所以这类方法只能在概率意义上规划到期望状态的附近。最终状态的偏差也会随着状态图中的顶点数的增加而指数收敛到零。而且与2.3节中离散化方法相似,这一类方法也难以满足多个敏感轴的约束。同时,这类方法大多是规划出一条可行的安全路径,并未能将动力学约束和角速度约束同时考虑在规划策略设计中,并且对于姿态机动过程中的最优性就难以满足。 由于航天器携带的工质推进燃料有限和特定任务的机动时间需求,航天器姿态控制系统设计在考虑各类运动约束的同时,还需要针对特定的性能指标优化。因此,基于数值优化的方法也被广泛的用于姿态规划的研究。这一类方法的核心思想是将给定的性能指标作为目标函数,把姿态运动学和动力学方程作为等式约束,并刻画运动过程中的各类物理约束成不等式约束,从而特定工况下的性能最优的控制问题转化为约束条件下数值优化进行求解,如图9所示。 针对求解姿态机动的最优控制问题,密歇根大学的团队[61-62]基于间接法将最优控制问题转换成了两点边值问题求解了约束下航天器的重新定向的问题,这一系列方法中使用的李群变分积分的离散化方法有助于提高离散化精度,提高了求解精度和效率。凸优化技术作为一种相对成熟的优化问题求解工具,近年来也在航天器运动中得到了广泛的研究[63]。华盛顿大学的Kim和Mesbahi[64]采用了凸优化的思路进行处理,针对 Planck 空间观测卫星等典型的实际型号的约束下姿态重定向任务,将姿态约束转化为凸的线性矩阵不等式(Linear Matrix Inequality, LMI)形式的约束,并证明了转化后的问题与原问题等价。文献[65] 针对更为复杂的软约束、动态约束以及混合约束进行约束凸化处理,解决了姿态机动中的凸优化规划问题。Sun和Dai[66]提出了基于二次约束二次规划(Quadratically Constrained Quadratic Programming, QCQP)的迭代算法。在文献[64] 的基础上,姿态禁止区约束及强制区约束被转化成了基于四元数的不等式约束,并考虑了姿态机动过程中存在的角速度约束和控制饱和限制。该方法采用半定松弛技术对将问题转化为带有秩约束的半定规划问题,提出了一种逐次迭代的秩最小化迭代算法,最后利用凸优化求解工具得到姿态机动的最优轨迹。此外,Tam和Glenn[67]也在Kim的工作的基础上,使用了混合整数规划算法,求解对应的航天器多约束姿态规划问题。 上述基于数值优化的方法是通过刻画最优问题并求其数值解,从而得到特定工况下的最优姿态机动轨迹。但是求解这一类问题往往需要较高的计算硬件支持和较长的求解时间,尤其是当约束非线性且相互耦合的时候,更会导致运算成本增加。此外,这类方法是基于数学模型的,它们的求解往往依赖于精确的模型信息,因此基于数值规划的方法也存在一定的局限性。 正如2.5节中分析,传统基于数值优化的方法存在求解效率低和模型依赖强等不足,特别是对于一些复杂的问题(如模型非完全精确已知的“灰/黑箱”问题、非凸形式的博弈问题等)很难有效地处理。值得注意的是,人工智能技术的近期进展为空间智能自主规划提供理论、方法及技术支撑[68-70]。基于元启发式的智能优化算法在航天器姿态机动中也得到了广泛研究,如遗传算法(Genetic Algorithm, GA)及其拓展方法[71-73]、粒子群算法(Particle Swarm Optimization, PSO)[74-76]以及差分进化算法(Differential Evolution, DE)[77]等。这些算法利用仿生学的特点和机制能够缓解传统优化算法中问题非凸造成的局部极小值的问题。 值得注意的是,近年来以强化学习技术为代表的新一代人工智能技术已经在各类无人系统中受到了重点关注[78]。这类方法的基本原理如图10所示,通过构建环境反馈(“奖励”或“惩罚”),从而激励智能体在环境反馈中学习调整当前策略,最终实现“奖励”最大化的执行策略[79]。因此,在利用环境反馈处理约束时,将期望的运动状态构造成“奖励”,将违背约束的运动状态刻画成“惩罚”是一种处理运动约束规划的有效途径。 在航天器姿态机动任务中,文献[80] 针对非合作目标抓捕任务,基于深度 Q 网络(Deep-Q Networks, DQN)学习算法设计了一套姿态镇定策略,该方法利用历史数据进行训练,不依赖于空间目标的质量参数,具有比较强的智能性和适应性。文献[81] 提出了一种基于近端策略优化算法(Proximal Policy Optimization, PPO)的姿态机动策略,在无需转动惯量信息的情况下,显著提升了性能。Elkin等[82]针对航天器姿态机动问题,提出了一个新型的强化学习框架,该框架利用地面高保真的数字仿真环境进行训练,同时由测量的运动状态更新仿真环境的数字模型,并近乎实时的将最新的姿态机动策略更新,实现了策略在线更新的运动规划。上述方法主要是针对无约束情况下的姿态机动,笔者团队[5]针对多约束下的航天器姿态机动问题,在自适应动态规划(Adaptive Dynamic Programming, ADP)框架下设计了一种在线学习的算法,结合历史数据与实时测量状态,在线近似求解最优问题对应的哈密顿-雅可比-贝尔曼(Hamilton-Jacobi-Bellman equation, HJB)方程,对姿态机动策略的实时更新,实现了在指向和角速度双重约束下的姿态重定向机动。文献[83] 进一步考虑了执行机构偏差,改进在线学习策略,实现了姿态约束和执行机构不确定性下的高精度姿态机动。上述方法首先设计了比例微分算法得到初始的规划策略,然后通过在线的“奖励”反馈完成策略的实时更新,实现了小计算代价的安全规避和性能的在线优化。 以强化学习为代表的人工智能方法是解决航天器运动规划的新途径,前述工作中约束的处理主要取决于环境“环境奖励”的构造,如何针对航天任务的需求,设计更为精准合理的“奖励量化”机制是一项有待研究的内容。此外,考虑到航天器机动任务的特殊性,利用小样本数据进行快速在线策略学习有着十分重要的作用,故设计高效的学习律是亟需突破的关键技术。 姿态控制是保障航天器稳定飞行或跟踪制导指令的关键技术之一。在实际工程中,比例积分微分控制(Proportional-Integral-Derivative control, PID)因其结构简单、参数调整直观、易于工程实现等优点,一直被广泛应用于航天器姿态控制系统的设计中[84]。然而,传统 PID 控制不能有效处理姿态控制设计面临的系统不确定性、多源干扰、执行机构故障、暂稳态性能约束以及测量信息不完备等广义约束,难以满足新兴空间任务对姿态控制系统高自主、高可靠和高精度的发展需求。近年来,国内外学者围绕航天器姿态控制问题(包括姿态镇定、姿态机动和姿态跟踪)开展了大量的理论与应用研究,提出了一系列先进的控制方法。下面将着重面向参数不确定性、多源干扰、执行机构故障和暂稳态性能约束,依次介绍自适应控制、抗干扰控制、容错控制、预设性能控制等姿态控制方法的研究进展。 航天器的惯量不确定性可能会导致控制精度下降,严重时甚至会造成系统失稳。基于“以变应变”思想的自适应控制可以有效处理参数不确定性问题。传统自适应控制方法大多基于确定等价(Certainty-Equivalence, CE)原则,其基本思想是[85]:首先在假设不确定参数已知的前提下进行反馈控制设计,而后用估计值替换控制律中的不确定参数,并设计相应的自适应律在线更新参数的估计值,保证闭环系统的稳定性以及系统跟踪误差的收敛。基于 CE 的自适应控制因思路简单、直观,在航天器姿态控制中得到了广泛的应用[19,86]。然而,在 CE 框架下,自适应律的设计主要是为了精确抵消由参数不确定性所引入的附加“扰动”项,但当参数估计无法收敛到它们的真值时,这种脆弱的抵消操作往往会降低闭环系统的暂态性能和鲁棒性。然而,参数收敛仅在参考轨迹满足严格的持续激励(Persistent Excitation, PE)条件时才能实现。 为了提高自适应控制性能,相关学者脱离CE原则,基于浸入与不变(Immersion and Invariance, I&I)技术提出了非确定等价自适应控制方法。I&I方法论最早是由Astolfi和Ortega[87]基于微分几何概念提出的。I&I自适应控制方法主要是通过在参数估计中额外增加一个函数项以构造一个微分流形,并设计控制律和自适应律使得所构造的流形不变且吸引,从而以鲁棒的思想处理系统参数不确定性。这一方法极大地放宽了 CE 自适应控制对 PE 条件的依赖。需要指出的是,I&I 自适应控制需要求解一个特定的 PDE 来构造微分流形,但对于航天器姿态动力学这类多输入非线性系统而言,PDE 通常无解析解,即所谓的“可积性障碍”。这一障碍极大地限制了传统 I&I 自适应控制在航天姿态控制中的应用。为了克服此问题,Seo 和 Akella[88]分别针对航天器姿态跟踪问题,提出了基于回归滤波的 I&I 自适应控制方法,通过引入状态和回归矩阵滤波器,构造了一个增广滤波系统,并利用增广滤波状态和滤波回归矩阵直接给出了PDE的解析解。文献[89]利用这一方法设计了I&I自适应姿态控制器。Karagiannis等[90]将动态缩放(Dynamic Scaling)技术应用到I&I自适应控制设计中,为克服可积性障碍提供了一个新思路。该方法通过引入状态滤波器,将原始回归矩阵中的积分变量按照一定方式替换为相应的滤波状态量,使回归矩阵可积,并给出ODE的近似解,之后设计动态缩放因子补偿近似解导致的误差。与文献[88]相比,基于动态缩放的方法只需对原系统进行低维的动态扩张便可实现与之相似的性能。Yang等[91]将该方法应用到了航天器姿态跟踪控制问题中,并改进了动态增益的设计,有效避免了高增益控制问题。Wen等[92]进一步改进了动态缩放因子,移除了文献[91]需要惯量矩阵最小特征值的假设。Xia和Yue[93]针对航天器抗退绕姿态稳定问题,提出了基于动态缩放的 I&I 自适应控制方法,并通过引入饱和的缩放因子,使得控制器不需要任何动态增益。本文作者团队将基于动态缩放的 I&I 自适应控制方法应用于航天器受限的姿态重定向中[4]。 CE 和 I&I 自适应控制方法均仅当回归矩阵满足 PE 条件时,才能保证参数估计收敛到它们的真值[94]。但 PE 条件较为严苛,在实际中通常难以满足。近年来,国内外众多学者都开展了放宽参数收敛对 PE 条件依赖的研究。Chowdhary 和 Johnson[95]在 MRAC 框架下,提出了一种基于并行学习(Concurrent Learning, CL)的自适应控制方法,通过并行使用丰富的历史数据和当前量测数据设计自适应律,可在系统状态仅满足宽松的有限激励(Finite Excitation, FE)条件下保证参数收敛。这一方法自提出以来就获得了广泛的关注与应用。Zhao 和 Duan[96]针对惯量不确定性下的组合体航天器姿态跟踪问题,提出了 CL 自适应律,精确地估计出了组合体未知的惯量参数。由于 CL 算法需要数据选取与存储,为使存储的数据尽可能多地包含线性无关元素,需要选择一个合适的记录方案,这极大地增加了算法设计的复杂度。而且,传统 CL 算法需要状态导数(如角加速度)来构造参数估计误差,但状态导数一般是不可测的信号。尽管可以使用固定点平滑器、滑模微分器等对状态导数进行在线估计,但这种处理方法对测量噪声比较敏感。为避免使用状态导数信息,Cho等[97]提出了复合自适应控制方法,无需状态导数信息,在 FE 条件下实现了参数收敛,而且由于其使用滤波回归的积分进行数据存储,也避免了在线数据选取。基于相似的思想,文献[98] 提出了复合学习控制方法,并成功应用于机械臂控制中。本文作者团队针对航天器姿态跟踪和多约束姿态再定向问题,基于复合学习思想,提出了几种自适应与学习控制方法,在保证高精度姿态控制的前提下,实现了惯量参数的在线辨识[99-100]。 虽然国内外研究人员在航天器姿态自适应控制方面取得了一定的进展,但现有的自适应控制方法大多要求惯量参数是常值或慢变的(近似于常值)。对于未知时变惯量条件下的航天器姿态自适应控制技术,尤其是时变惯量参数进行在线辨识,有待系统性的探索。 航天器在轨运行期间所受的多源干扰极大地影响了航天器姿态控制的精度及稳定度。姿态控制设计需要针对性地抑制或抵消这些干扰,以提升姿态控制系统的抗扰能力和控制精度。现有航天器姿态抗干扰控制方法可大致归为3类:①鲁棒控制方法;②自抗扰控制方法;③基于干扰观测器的控制方法。 鲁棒控制诞生于20世纪 70 年代末期,最初是为解决航空航天领域的控制问题,直到 1988 年著名的 DGKF 方法发表[101],相关理论才趋于成熟。至今,鲁棒控制仍是最为广泛使用的姿态抗干扰控制方法。Liu等[102]提出了一种非脆弱的鲁棒H∞控制方法,解决了存在建模不确定性、控制摄动、外部干扰和控制输入限制的挠性航天器姿态稳定和振动抑制问题。一些学者结合H2和H∞鲁棒控制方法,提出了混合H2/H∞鲁棒姿态控制方法[103-104]。Luo等[105]针对存在外部干扰的航天器姿态跟踪问题,结合鲁棒控制和最优控制方法,提出了一种H∞逆最优控制器,实现对干扰的H∞最优。Wang 和 Li[106]提出了一种鲁棒最优控制方法,解决了存在执行机构安装偏差和干扰的航天器姿态稳定问题。 变结构控制凭借其对不确定性和干扰的强鲁棒性,也是最为广泛应用的鲁棒抗干扰方法。笔者团队[107]针对挠性航天器大角度姿态机动问题,结合主动振动抑制技术,提出了滑模控制(Sliding Mode Control, SMC)方案,有效抑制了外部干扰和挠性振动。为实现有限时间控制,相关学者也提出了终端 SMC 方案[108-109]。针对存在外部干扰和控制幅值受限的航天器姿态控制问题,Wallsgrove 和 Akella[110]提出了一种饱和的光滑变结构姿态控制方案,通过构造时变的滤波变量,并引入一个锐度函数,有效抑制了干扰对闭环系统的影响,实现了渐进的姿态收敛。本文作者团队基于文献[110] 也提出了几种光滑的变结构控制方法[111-112],解决了控制输入和角速度受限下的航天器抗退绕姿态稳定问题,在干扰下实现了姿态和角速度的渐进收敛。鲁棒控制方法的核心思想是“以不变应万变”,即考虑系统可能面临的“最坏”扰动情况,设计一个结构不变的鲁棒控制器,实现对有界扰动的有效抑制,故而具有较强的保守性。相比而言,自抗扰控制和基于干扰观测器的方法通过对扰动进行估计和补偿,可有效减小控制器的保守性。 自韩京清[113]1998 年提出自抗扰控制(Active Disturbance Rejection Control, ADRC)以来,该方法一直受到控制界的广泛关注,并已成功应用于航空航天、工业控制等领域。ADRC 继承了经典 PID 控制的误差反馈精髓,并引入扰动估计补偿技术,使其不依赖于被控对象精确的数学模型,对干扰具有较好的抑制能力。ADRC 一般由跟踪微分器、扩张状态观测器(Extended State Observer, ESO)、非线性状态误差反馈控制律和扰动补偿等几个环节组成[18]。Xia 等[18]针对航天器姿态跟踪问题,提出了一种基于 ESO 的 SMC 方案,通过设计 ESO 对系统集总干扰进行估计补偿,极大地放宽了传统 SMC 的保守性。文献[114] 针对外部扰动、输入/测量噪声及饱和约束等影响下的无拖曳卫星位姿控制问题,采用基于扩展状态的卡尔曼滤波器对系统状态和扰动进行估计,并设计自抗扰控制器,实现了无拖曳卫星的联合控制。 尽管前述的非线性 ADRC 方法具有参数效率高、干扰观测性能好等突出优点,但其结构较为复杂,需要调节的参数较多,导致参数整定困难。针对此问题,美国 Cleveland State University 的Gao[115]提出了线性 ADRC 方法,给出了基于观测器带宽的观测器增益整定方法,通过将多参数整定问题简化为单参数整定问题,极大地简化了控制器设计和理论分析。Bai等[116]针对存在干扰的航天器姿态跟踪问题,采用线性 ESO 对外部干扰进行估计和补偿,并设计一种自适应控制方法,实现了姿态和角速度跟踪误差的快速高精度收敛。除此之外,还有很多基于 ADRC 的姿态抗干扰控制成果,但限于篇幅,这里不再一一罗列。现有 ADRC 方法在测量噪声明显时,因观测器增益限制,极易导致扰动估计不精确,进而造成控制性能下降。 基于干扰观测器的控制方法(Disturbance Observer Based Control, DOBC)起源于 20 世纪 80 年代,最初是日本学者 Ohishi等[117]针对直流伺服电机的控制问题,提出了一种频域干扰观测器对伺服电机干扰进行估计和补偿。DOBC 方法的基本思想是设计干扰观测器对系统的内外干扰进行估计和前馈补偿,以抵消干扰对系统的影响,并结合其他控制方法,实现特定的控制需求。由于结构简单、参数整定方便,DOBC 方法自提出以来便在控制领域得到了广泛关注。尽管频域干扰观测器被成功应用于各类系统,但其分析设计均基于线性化的模型和线性系统理论,极大地限制了其应用范围。 英国 Loughborough University 的陈文华[118]于2000年首次利用时域方法提出了一种非线性干扰观测器,并应用于机械臂控制中实现了精确的摩擦估计和补偿。此后,非线性DOBC理论得到了迅速发展。针对航天器姿态控制系统,该方法的结构如图11所示。Sun 和 Zheng[119]针对存在测量噪声和控制输入饱和的航天器姿态稳定问题,将测量噪声、参数摄动和外部干扰当成“集总干扰”,采用非线性 DOB 对集总干扰进行估计和前馈补偿,并基于抗积分饱和补偿器设计了饱和鲁棒控制器。Zhang等[120]结合积分型 DOB 和终端滑模控制技术,设计了自适应滑模控制器,实现了有限时间姿态跟踪。Zhu等[121]针对挠性航天器的主振动抑制和姿态抗扰控制问题,分别设计了自适应 DOB 和挠性振动观测器,有效补偿了集总干扰和挠性振动。北京航空航天大学吴忠团队分别设计了有限时间 DOB[122]和迭代学习 DOB[123],并应用于挠性航天器姿态控制中。 值得注意的是,航天器姿态控制系统往往会受到模型不确定性、未建模动态、时滞、执行器误差、测量噪声以及外部环境干扰等内外部多源干扰的影响,这些干扰具有不同的表征形式,如范数有界变量、谐波变量、阶跃变量、非高斯/高斯随机变量以及变化率有界变量等[124]。传统的 DOBC 大多仅能对单一干扰进行补偿,没有充分挖掘出各类干扰的内在特征,并有针对性地进行精细化补偿和抑制。文献[125-126] 在传统 DOBC 的基础上,首次提出了复合分层抗干扰控制方法,在对系统干扰进行分析和分类建模的基础上,采用内环+外环的双环控制结构,实现对系统多源干扰的精细估计和补偿,该方法目前已在航天器、机器人等系统中进行了应用,并取得了较好的效果。Zhu等[127]结合 ADRC 和 DOBC 方法提出了一种增强的复合抗扰控制方法,该方法建立了一个外部模型对挠性振动引起的干扰进行描述,并将参数不确定性、环境干扰等其他干扰归结为一个微分有界的等效干扰,然后利用 DOBC 对挠性振动干扰进行精细估计与补偿,并采用 ADRC 补偿其他干扰,相较于单一的 DOBC 或 ADRC 方法具有更强的抗扰能力。Yu等[21]首次提出了干扰可估计性和可补偿性概念,并与文献 [127] 相似,结合 ADRC 和 DOBC 技术设计了一种增强的抗干扰姿态控制器,实现了挠性航天器的精细干扰补偿和高精度姿态控制。 虽然过去20年 DOBC 技术取得了长足的发展,并在航天器姿态抗干扰控制中得到了应用与验证,但是提高 DOBC 在大延时、高对抗和强干扰等复杂环境下的精细抗干扰能力,仍是一项有待深入研究的工作。 世界各空间机构在航天器的设计、生产及其在轨运行过程中,都非常重视航天器的可靠性和操作的安全性。但受制造工艺水平、成本限制等客观因素的制约,以及高/低温、强辐射、强电磁干扰等恶劣太空环境的影响,航天器故障事件仍时有发生,如太阳帆板损坏、陀螺仪失效、遥测指令系统异常等。航天器故障给航天器的安全性带来了极大隐患。据统计表明[128],1980—2005年间在轨航天器所发生的 156 起故障事件中,姿态和轨道控制系统(Attitude and Orbit Control System, AOCS)与电力系统(Power)故障占总故障的 59%。进一步分析故障对任务的影响,发现近 65% 的故障是非致命性故障,致使了航天任务降级,而近 40% 的故障是致命性的,导致航天任务完全失败,造成了巨大的经济损失。 姿态控制系统因功能和结构复杂,是航天器故障事件最高发的子系统之一。根据文献[128]可知,1980—2005年发生的 156 起故障事件中AOCS 故障占总故障的 32%,而且近 50% 的 AOCS 故障是由反作用飞轮、动量轮、推力器等姿轨控执行机构故障引起的。航天器长期在轨运行期间,这些姿轨控执行机构需要频繁工作以驱动航天器完成指定任务,这也是它们故障高发的原因。表2 和表3 分析了典型的推力器和反作用飞轮故障案例。由此可见,执行机构故障轻则会导致航天器任务降级、寿命缩减,重则直接致使航天器完全失效甚至失控解体,造成巨大的经济损失和灾难性的后果。因此,使航天器具备自主故障处理能力尤为重要。 表2 推力器故障典型案例Table 2 Typical cases of thruster faults 表3 反作用飞轮故障典型案例Table 3 Typical cases of reaction wheel faults 为满足航天器日益提升的安全性、可靠性和可维护性需求,迫切需要发展容错控制(Fault-Tolerant Control, FTC)技术,使航天器具备自主故障处理能力。FTC 发端于航空航天高可靠性需求,20 世纪 80 年代美国空军提出了“自修复飞行控制系统”等概念,以保证飞行器在故障情况下仍能安全着陆。文献[129]对FTC技术进行了系统性梳理和回顾。根据文献[130],现有的航天器姿态FTC方法可分为2大类:被动FTC和主动FTC。 被动 FTC 本质上属于“以不变应万变”的鲁棒控制方法,在设计过程中需要充分考虑潜在的故障,并将它们视为系统不确定性,而后设计一个鲁棒控制器实现容错控制。该方法不需要故障的在线信息,且无需进行控制重构,能够同时处理多种类型故障,具有设计简单、工程实用性强等优势,目前已在航天器控制领域得到了广泛关注。现有的航天器姿态被动 FTC 方法主要集中于“自适应 + X”方法(如自适应 + 滑模控制、自适应 + 鲁棒控制等)。Cai等[131]针对航天器姿态跟踪问题,提出了一种“间接自适应+滑模控制”的鲁棒容错控制方法,该方法不仅能够在有限推力下应对推力器故障,还对参数不确定性和外部干扰具有强鲁棒性。Shen等[132]结合终端滑模控制和自适应控制技术,研究了有限时间FTC问题。Xiao等[133]研究了刚柔耦合航天器的姿态跟踪问题,考虑执行机构故障、测量噪声、未知模态位移、参数不确定性和外部干扰等,设计了自适应容错控制器,采用序列Lyapunov方法分析了跟踪误差的保性能收敛界。近年来,本文作者团队[134-135]提出了“自适应+预设性能控制”的航天器姿态FTC方法,在参数不确定性、外部干扰和执行机构故障下实现了姿态跟踪误差的预设性能收敛。尽管被动FTC能够有效处理一大类执行机构故障,且对干扰具有强鲁棒性,但控制器的保守性较强,难以恢复理想的控制性能。 不同于被动 FTC,主动 FTC 方法主要是通过引入一个故障检测和诊断(Fault Dection and Digonosis, FDD)算法对执行机构故障进行在线实时检测与诊断,而后利用 FDD 模块的诊断信息重构控制器,以“精准诊断-对症下药”的思想主动地应对执行机构故障,保证整个系统在故障下仍具有可接受的性能。主动 FTC 方法的框架如图12所示,该方法能够充分利用系统的物理和解析冗余,主动地应对执行机构故障,故具有较小的保守性。主动 FTC 系统一般包含故障诊断与容错控制2部分内容,而故障诊断又分为 3 部分:① 故障检测,即检测出系统是否发生故障与故障发生的时间;② 故障隔离,即获知系统哪个部件发生故障以及故障类型和发生的具体位置;③ 故障辨识,即根据系统测量信息辨识出故障大小。目前,大量学者对航天器姿态控制系统的故障诊断问题进行了研究,现有成果可划分为基于模型的方法、基于数据的方法和基于知识的方法3大类。哈尔滨工业大学沈毅等[136]和笔者团队[137]已对现有航天器姿态控制系统的故障诊断算法进行了梳理与总结,这里不再详述。尽管故障诊断技术取得了一些的研究成果,但大多方法在多源干扰的影响下面临故障虚警率高、隔离难、辨识精度低等问题,如何提高干扰下的故障诊断精度有待深入研究。 接下来,重点回顾故障辨识与容错控制方法的研究进展。Shen等[138]研究了姿态主动 FTC 问题,提出可避免虚警的故障检测方案,并构造了指数收敛的间接故障辨识器对系统总故障进行估计,在此基础上进一步设计了自适应滑模容错控制器,在满足输入饱和的前提下有效补偿执行机构故障对系统的影响。笔者团队[139]针对航天器单框架控制力矩陀螺的故障诊断问题,提出了一种基于神经网络的干扰观测器在线学习周期干扰,实现了故障和干扰的解耦,并基于神经网络和自适应估计器设计了故障诊断方案,实现对控制力矩陀螺故障的隔离和估计。近年来,一些学者也将执行机构故障和干扰统一归结为“集总干扰”,并基于 ADRC 或 DOBC 方法提出了一系列容错抗干扰控制方法[140-142]。笔者团队[142]提出了基于迭代学习干扰观测器的姿态容错抗干扰控制方法,并通过硬件在环实验验证了算法的有效性。Gui[143]研究了基于观测器的航天器姿态 FTC 问题,考虑执行机构故障、惯量不确定性、外部干扰以及状态估计误差,设计了一种连续滑模容错控制器,并使用序列 Lypunov 方法预测了稳态跟踪误差的收敛界。 基于控制重分配的容错控制方法具有故障发生时无需改变控制器结构的特点,也被广泛应用于主动 FTC 系统设计中。Shen等[144]针对航天器姿态跟踪问题,基于故障辨识结果,结合滑模控制和非鲁棒控制分配技术,提出了一种容错控制分配方法,该方法可充分利用健康和尚未完全失效的执行机构应对故障;随后,Shen等[145]又进一步提出了一种鲁棒容错控制分配方案。Li等[146]考虑执行机构故障、控制输入饱和以及外部干扰,提出了一种基于闭环控制分配的姿态 FTC 方法,在控制输入饱和限制下,通过将基准控制信号分配到冗余执行机构,并将分配误差纳入控制闭环,保证了闭环系统的稳定性。笔者团队[147]也提出了一种闭环的鲁棒容错控制分配方法,充分考虑故障估计误差,将控制分配问题描述为一个鲁棒最小方差问题,并给出了相应的解析解,克服了传统控制分配方法仅能给出数值解,且缺乏严格闭环稳定性保证的局限。 随着航天器星载设备集成化程度和航天任务品质需求的不断提升,以及空间对抗态势的日益升级,航天器发生执行/传感故障以及部件损伤的概率剧增。尽管目前航天器容错控制技术在理论和应用方面均取得了显著的进展,但针对航天器结构性故障(如航天器受攻击或撞击而发生帆板损坏等)的容错控制技术仍有待研究。 为确保航天器高品质地完成深空探测、在轨服务、空间对抗等新一代空间任务,姿态控制系统的设计需要考虑第1.4.4节总结的暂稳态性能要求。然而,现有的非线性控制方法(如滑模控制、自适应控制等)大多都侧重于分析闭环系统的稳定性与输出误差的稳态行为,缺乏对暂态性能指标的分析与保证。尽管混合H2和H∞鲁棒控制[148]和L2增益性能指标[149]可以分析闭环系统的暂态性能,但所引入的性能指标均与轨迹导向的暂态性能没有预先确定的关系,因此需要繁琐的参数选取才能获得期望的暂态性能。希腊学者 Bechlioulis 和 Rovithakis[150]提出了预设性能控制(Prescribed Performance Control, PPC),为保证控制系统暂稳态性能提供了崭新的设计思路。该方法的核心思想是通过引入性能函数为受控系统的状态或误差设定性能包络,刻画收敛速度、最大超调量和稳态误差等暂稳态控制性能,如图13所示,并结合误差转换技术和非线性控制方法,保证状态或误差严格在预设的性能包络内收敛。由于 PPC 框架并没有指定特定的控制器设计方法,故而可以根据实际控制需求,利用现有先进的非线性控制方法(如 SMC、DOBC、自适应控制等)对误差转换后的系统进行控制器设计。 鉴于 PPC 方法在保证系统暂稳态性能上的优势,该方法自 2008 年提出以来便得到了大量的应用。文献[151-152] 对航天器姿态 PPC 方法的研究进展和未来趋势进行了综述。考虑 PPC 方法的鲁棒性、抗干扰性和容错能力,本文从新的视角对航天器姿态 PPC 方法的进展进行重新梳理,将现有方法划分为2大类:“PPC + 估计/观测”方法和无模型 PPC 方法,其中第一类方法主要包括“PPC + 自适应控制”“PPC + DOBC”“PPC + 神经网络逼近”等。本文作者团队[89]针对航天器逼近操作问题,将空间运动约束转换为位姿跟踪误差的暂稳态性能约束,并考虑航天器质量特性不确定性,提出了一种 I&I 自适应 PPC 方法,能够保证航天器按照预设的性能要求完成对空间目标的逼近操作,且在逼近过程中严格遵循空间运动约束。此外,笔者团队[134-135]还研究了执行机构故障和输入饱和下的航天器姿态跟踪 PPC 问题,提出了两种基于障碍函数的自适应容错 PPC 方案,能够在执行机构故障和饱和下保证姿态跟踪误差的暂稳态性能要求。Liu 等[153]考虑外部干扰和执行机构影响下的航天器姿态跟踪问题,提出了一种自适应容错 PPC 方法,实现了姿态和角速度跟踪误差的预设性能收敛。哈尔滨工业大学Huang和Duan[154]针对组合体航天器姿态跟踪 PPC 问题,考虑惯量不确定性、外部干扰、执行机构故障和饱和等因素,提出了一种基于非线性 ESO 的抗积分饱和容错 PPC 方案。 尽管前述的姿态 PPC 方法具备较强的鲁棒性、抗干扰性和容错能力,但大多需要在线估计或观测,致使算法复杂度高、计算量大,在星载计算资源严重受限的情况下,难以在轨应用。为了提高 PPC 算法的实用性,近年来一些学者探究了低复杂度的无模型 PPC 方法[155],并在航天控制领域得到了应用。Zhou等[156]针对 SO(3) 描述下的航天器姿态跟踪问题,提出了一种无坐标的鲁棒 PPC 方法,该方法具有简单的控制器结构,无需动力学参数信息,但对外部干扰具有强鲁棒性。西北工业大学殷泽阳等[157-159]针对航天器姿态稳定、跟踪和组合体航天器姿态接管控制问题,提出了几种低复杂度的无模型 PPC 方法,这些方法无需对模型参数和干扰进行先验估计或在线辨识,能够保证系统输出在存在参数不确定性和外部干扰的条件下仍能满足预设的暂稳态性能要求。特别的是,文献[159] 基于终端滑模设计了一个指定时间性能函数,并在此基础上提出了无模型双层 PPC 方法。Hu等[160]进一步为挠性航天器姿态跟踪设计了一种无模型双层 PPC 方法。 现有姿态 PPC 方法大多仅能处理暂稳态性能约束,而难以兼顾各类运动和物理约束。文献 [161] 通过引入一个基于正系统理论的辅助系统来放宽饱和发生时的性能约束包络,克服了控制输入饱和下的 PPC 设计难题,但该方法仍无法用于处理运动约束下的 PPC 设计问题。如何在多运动和物理约束并存的情况下,形成有效的姿态 PPC 方法,完成多约束下的航天器姿态预设性能控制是亟待解决的难题。 除了3.1~3.4节介绍的4种姿态控制方法外,一些典型的姿态控制方法还有: 1) 航天器姿态输出反馈控制。由于成本和容积的限制,一些卫星(尤其是小型化卫星)通常不装备角速度测量元件,或因传感器故障,导致其无法获得角速度测量信息。输出反馈控制能够在角速度信息缺失下实现控制目标。传统方法基于航天器姿态动力学的无源性(Passivity),利用姿态信息设计输出反馈控制器[162]。但这类方法需要在控制设计中额外引入一个动态环节,降低了系统的动态响应。基于状态观测器的输出反馈控制方法是另一种被广泛应用的方法。美国德克萨斯大学奥斯汀分校的Akella等[163]提出了全局渐近收敛的角速度观测器,并利用观测信息设计了类 PD 姿态控制器,解决了观测器和控制器之间分离性质(Separation Property)难以建立的难题,证明了闭环系统的稳定性。 2) 航天器姿态事件触发控制(Event-triggered Control, ETC)。现有航天器姿态控制方法大多是时间驱动的,即控制指令更新和通信是周期性采样的。尽管周期性采样易于工程实现,但从资源利用的角度来看,周期性采样和控制方式不可避免地会导致大量的计算和通信资源浪费。ETC 为克服这一问题提供了解决思路,该方法通过预先设定阈值和触发条件,保证控制指令和通信仅在特定事件触发时才执行,极大降低了控制指令和通信的更新频率[164]。文献[165] 首次在 ETC 框架下研究了航天器的姿态稳定控制问题,通过设计基于状态的触发条件保证姿态信息和控制指令只在离散的触发时刻被传递和更新。笔者团队[166]在角速度和通信资源受限的情况下,提出了一种基于神经网络的自适应事件触发姿态机动控制算法,有效降低了通信资源消耗。 3) 航天器姿态智能控制。随着人工智能技术的迅猛发展,在航天器控制中得到了广泛的关注与应用。在文献[167-168]中,全面分析并展望了智能方法在解决航天任务中执行器故障、参数不确定、控制性能优化等问题的案例,为多约束下的航天器姿态控制设计提供了崭新的途径。针对模型参数不确定性,文献[169]提出了一种智能 PD 挠性航天器姿态控制器,利用径向基函数(Radial Basis Function,RBF)网络以实现对未知扰动项的补偿。Schram等[170]则设计了智能自适应姿态控制算法,利用强化学习技术对不确定性进行在线逼近,实现了高精度姿态跟踪。在文献[171] 中,基于深度神经网络的参数估计设计了自适应鲁棒姿态跟踪算法。Li等[172]针对分布式航天器的姿态协同跟踪问题,设计了自适应神经网络逼近系统不确定项,从而进一步设计反馈控制器。面向执行机构故障,Baldi等[173]使用 RBF 网络建立主动容错控制系统对故障产生的控制偏差进行补偿,实现了容错故障跟踪控制。Chen和Tao[174]也采用 RBF 网络构建闭环自适应容错控制器,实现了存在未知死区和不确定扰动的姿态高精度跟踪。文献[175] 考虑了多个控制力矩陀螺多种故障发生的工况,采用深度神经网络建立了自适应容错控制架构,实现了高精度的容错控制。针对控制性能的优化,Liu等[176]针对组合航天器的姿态跟踪,基于 Q-learning 的方法实现利用离线数据学习的控制器设计。在文献[177] 中,使用深度神经网络替代传统的 PID 算法设计姿态跟踪控制器,并利用遗传算法进行网络初始权值的选取,提升了智能算法的部署效率。Zhang等[178]设计了一种 PID-Guide TD3 的学习算法,用来训练航天器姿态控制器, 利用 PID 控制器作为引导训练,提高了传统 TD3 算法的离线学习效率。笔者团队[179-181]最近提出了一系列基于在线学习的在线强化学习控制策略,实现了航天器在线最优姿态控制,并在半物理实验平台上得到了验证。 限于篇幅,其他方法在这里不再介绍。 针对航天器姿态规划与控制面临的各类复杂约束,自主规划与控制技术从满足飞行任务需求出发,从系统级、任务级的规划,发展到设备级的精细化规划与控制,在保障航天器安全与健康运行、延长航天器的在轨寿命具有显著的学术价值和应用前景。从当前的研究进展和需要解决的问题来看,建议多约束姿态规划与控制技术在未来研究的发展方向为如下几方面: 1) 复杂不确定环境下多约束多目标在线姿态规划技术 传统规划方法大多是在任务执行前,根据航天器初始姿态和目标姿态,预先规划出一条可行轨迹。然而,航天器在执行空间对抗、深空探测等任务的过程中,复杂不确定的飞行环境、突发事件造成的任务目标改变等因素会导致预先规划难以正常执行。所以,需要研究复杂不确定环境下的在线快速重规划方法,以快速应对预先规划失效的问题,在保证航天器在轨飞行安全的前提下尽可能地完成任务目标。另一方面,随着空间任务日趋复杂,姿态规划问题逐渐由传统单目标运动规划向多约束多目标运动规划发展,需要考虑执行时间、能量消耗等性能指标,且面临的约束更加复杂,除了常见的静态硬约束外,还可能存在动态软约束(如时变指向约束、进入禁止区的时长限制)等。因此,考虑静态硬约束、动态软约束等复杂多约束,并综合各性能指标,研究复杂不确定环境下的多约束多目标在线姿态规划技术是未来值得探讨的问题。 2) 控制系统能力退化下的柔性任务重构与多约束姿态控制一体化技术 当一个或多个执行机构发生完全失效、卡死等严重故障时,会导致航天器姿态控制系统能力退化,甚至导致系统由过/全驱动系统变为欠驱动系统,严重影响了既定空间任务的顺利执行以及航天器在复杂环境下的运行安全。已有成果大多假设在执行机构故障条件下,姿态控制系统仍是过/全驱动的,并侧重于保证系统的稳定性和稳态性能,而对故障下的系统剩余驱动能力量化分析的研究尚不多见。从工程的角度来看,控制系统能力退化可能会导致既定的任务无法完成,需要进行在线任务重构(如任务降级等),以确保控制系统的剩余驱动能力能够顺利完成任务。另一方面,控制系统能力下降,尤其是导致系统欠驱动的情况,会显著减小航天器姿态机动路径的可行空间,给多约束姿态规划与控制设计带来了巨大挑战,目前鲜有这方面的研究。因此,亟需开展控制系统能力退化下的柔性任务重构与多约束姿态控制一体化关键技术研究,突破控制系统能力量化评估、柔性任务重构、欠驱动系统姿态可行空间与能控性分析等关键技术,重点解决欠驱动系统的多约束姿态规划与控制难题。 3) 基于“数字孪生 + 深度强化学习”的多约束姿态规划与控制技术 随着计算机硬件算力的显著提升,考虑到空间环境复杂、未知因素多等特点,以深度强化学习为代表的人工智能技术应用于规划与控制也将是必然的趋势。然而,这类方法大多是探索驱动的,即需要通过积累大量的“动作-反馈”数据进行学习训练,从而形成最佳策略。但是,对于空间任务来说,考虑到在轨燃料稀缺、安全性以及部件寿命,航天器不能进行大量的“反复试错”,无法获取丰富的经验数据。数字孪生技术的出现为这一问题提供了解决思路。数字孪生可将航天任务中的复杂环境和航天器系统进行数字化镜像,从而对约束场景、执行机构、传感器等虚拟映射,进而实现环境模拟,约束演化,故障的预测诊断等。因此,利用数字孪生技术可以让智能算法积累与真实环境近乎相同的“探索经验”,并根据传感的数据实时更新孪生模型。通过“数字孪生 + 人工智能”的模式,实现数据模型混合驱动的多约束在线规划与控制必将是今后发展的重要方向。 4) 基于合作博弈强化学习的细胞卫星姿态接管控制技术 随着微小卫星技术的发展,以利用多个细胞卫星附着在失效航天器上实施接管控制为代表的技术,为航天器的在轨维护提供了新的发展方向。在细胞卫星附着组合后,航天器具有冗余的执行机构和较高的可靠性。为了使各个细胞卫星能够协调控制并使得控制的代价消耗最小,对于每个细胞卫星来说都是一个合作博弈的过程,即“付出最小的单体代价,实现整体最优目标”。而传统的控制技术难以应对这一需求。基于微分博弈的合作控制策略是实现这一任务的解决方案。考虑到细胞卫星附着后的组合体质量特性未知,且多体博弈控制所转化而成的数值优化问题较为复杂,难以利用已有基于模型的数值求解工具进行求解。而以自适应动态规划为代表的强化学习技术为这一新兴任务提供了解决途径。因此,研究基于强化学习的合作博弈控制技术是面向细胞卫星接管控制为代表的新兴航天任务的技术基础,也是未来航天器在轨服务技术发展的新方向。 5) 多约束下的航天器编队飞行分布式协同规划与控制技术 近年来,随着星载计算、通信、传感等技术的迅猛发展,利用多颗小型卫星构成一个大规模的航天器编队系统,并通过无线通信与感知形成特定的构型进行自主协同飞行,协作地完成传统大型单航天器无法完成的大孔径、长基线等新兴空间探测和成像任务,已成为航天技术发展的新趋势。相比于单航天器系统,编队系统具有研发周期短、适用性强、容错性高等特点,以及快速的空间响应能力和空间攻防对抗下的空间任务保护与生存能力,在科学研究、国民经济以及国防建设等领域发挥着至关重要的作用。在编队系统运行的过程中,各航天器之间需要保持通信并避免碰撞,这给协同规划与控制算法设计带来了复杂约束,同时空间环境往往是高动态的,任务也可能是变化的,这都对规划和控制算法的在线适应能力提出了更高的要求。另外,编队飞行任务可能会发生一个或多个成员故障或损毁、新航天器补充等情况,这对编队系统的任务协同、编队飞行安全以及通信拓扑带来了巨大挑战。现有的编队系统协同规划与控制方法大多没有考虑复杂约束条件,且大多采用集中式处理方式,具有实时性差、响应慢、一致性差等缺陷。因此,亟需突破现有局限,设计具有强约束处理能力的航天器编队分布式协同规划与控制技术、成员故障或损毁下的“任务重规划-编队构型重构”一体化在线规划与控制技术等,保证多约束下的航天器编队系统飞行安全和稳定性。 随着航天器自主规划与控制技术的不断发展以及在深空探测、在轨服务等一系列航天任务的成功应用,极大提升了航天器的自主性和智能化水平。多约束姿态规划与控制技术是保证航天器在复杂空间环境下稳定可靠运行并安全实施各类空间任务的关键,因此受到了广泛的关注与深入的研究。本文在总结航天器姿态机动任务所面临的各类约束的基础上,梳理了现有航天器多约束姿态规划与控制方法的设计思路,并对各方法的优缺点和部分代表成果进行了综述。最后,面向航天任务未来需求,给出了航天器多约束姿态规划与控制技术的发展方向。
1.4 广义约束
2 多约束姿态规划方法
2.1 几何方法
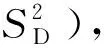
2.2 势函数方法
2.3 离散化方法
2.4 基于随机规划算法的姿态规划方法
2.5 基于数值优化的姿态规划方法
2.6 基于人工智能的姿态规划方法
3 航天器姿态控制方法
3.1 航天器姿态自适应控制
3.2 航天器姿态抗干扰控制
3.3 航天器姿态容错控制
3.4 航天器姿态预设性能控制
3.5 其他航天器姿态控制方法
4 发展趋势
5 结 论
