含有L21范数正则化的在线顺序RVFL算法

季江飞，郭久森

（浙江理工大学 信息学院，杭州 310018）

0 引言

迄今为止，在与机器学习有关的诸多研究方向中，人工神经网络正起着越来越重要的作用，常见的相关应用包括图像处理、模式识别和控制等领域。当下的研究也已表明，针对不同的预测问题，只要选定了单隐层前馈网络（SLFN）的激活函数，就能够确定相应的决策边界。

单隐层前馈网络结构简单，训练代价小，在许多场合中都有不俗表现。目前经常见到的SLFN有极限学习机（Extreme Learning Machine，ELM）和随机向量函数连接网络（Random vector functional-link network，RVFL）。其中，ELM网络结构简单，训练和预测时计算速度较快，在做分类时有较好的性能。然而现如今的批处理系统在执行任务过程时数据会不断更新，如果反复进行批量训练，就会使计算成本偏高。基于此，则有学者提出了在线顺序的极限学习机（OSELM），能够在线地训练模型，不断更新输出权重。RVFL也是一种SLFN网络，在结构上与ELM类似，最主要的不同就在于RVFL直接将输入层与输出层做了直接映射。尽管RVFL在一定程度上提升了网络复杂度，但也提升了网络的泛化能力。为了降低奇异点和噪声的影响，引入了核函数来替代激活函数，再无需对隐藏层神经元数量进行调整，但是核函数的参数选择上却又面临了灵活多样、难以固定的困扰。Zhang等人使用了在线的RVFL网络来预测高炉铁水质量，但是并未引入正则化思想，神经网络的泛化能力略有不足。Zhou等人使用范数的方式提升结构的稀缺性，通过整体消除神经元来降低模型的内在复杂性，降低损失函数中的经验损失和结构损失。

综合前述研究，本文将在线顺序模式引入RVFL，使其具有即时处理新输入的小块训练集的能力，而不用重复计算整体大量的数据集。同时，利用范数对输出权重的表达进行正则化，可有效降低模型的内在复杂性。

1 相关知识

1.1 随机向量功能连接网络

图1 RVFL的网络结构Fig.1 Network structure of RVFL

其中，（）为激活函数；w为输入权重，w＝［w，w，，w］；b为隐含层增强节点的偏置；β＝［β，β，......，β］为输出权重。w和b一般是随机确定的。

公式（1）可以简化成矩阵，矩阵形式为：

其中，

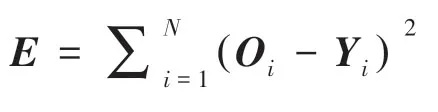
相较于传统的RVFL网络，正则化的RVFL能够提升网络的泛化能力，并能有效地预防模型的过拟合问题。常用的做法是求出训练误差和输出权重的最小值：

其中，输出的误差，是正则化系数，用于权衡训练误差和模型复杂度之间的影响。为了求得该最小值，可以通过将RVFL与有关的梯度设为零，进而推得的封闭形式解为：

其中，是维度为（）的单位矩阵。

1.2 正则化RVFL和损失函数的L21范数

在数据集的收集和整理的过程中，难免会录入一些受到噪声影响或者偶然性较大的数据点，这些由于人为因素或环境因素造成的误差，可能会使由常规样本训练而来的神经网络的性能难以达到预期。为了减少或者消除奇异点所带来的影响，这里定义了正则化和损失函数在模的最小化表达：

从上文对模的定义可知，对矩阵处理时先按行求其范数，再对结果求范数，如此操作能够将权重矩阵的部分行值减小到零。从而达到剔除可忽略不计的特征值的目的，同时也能减少网络的复杂性。基于KKT条件，可以得到最优解：

为了计算输出权重的解，分别对α，β，e求偏导并使其为零，那么就可以得到输出权重的最终解为：

2 含有L21范数的OSRVFL

RVFL能够批量训练全部个样本值，而在实时场景中，样本数据可能会不断地更新，此时RVFL网络则要去重新计算所有的训练数据。为了能够对更新的数据进行实时处理，故将研究重点关注在即时的数据上，引入了在线顺序的方式。通过不断地调整新参与的训练数据与已有数据之间的关联关系，计算和更新输出权重。让网络对新样本也能有好的预测效果，同时又大大减少了重复训练整块样本数据的计算量。

文中不妨假设初始训练样本数，那么初始输出权重可以由初始输出矩阵和输出向量得到：

其中，是一个的对角矩阵。当一个大小为的新数据块加入时，此时的输出权重有：

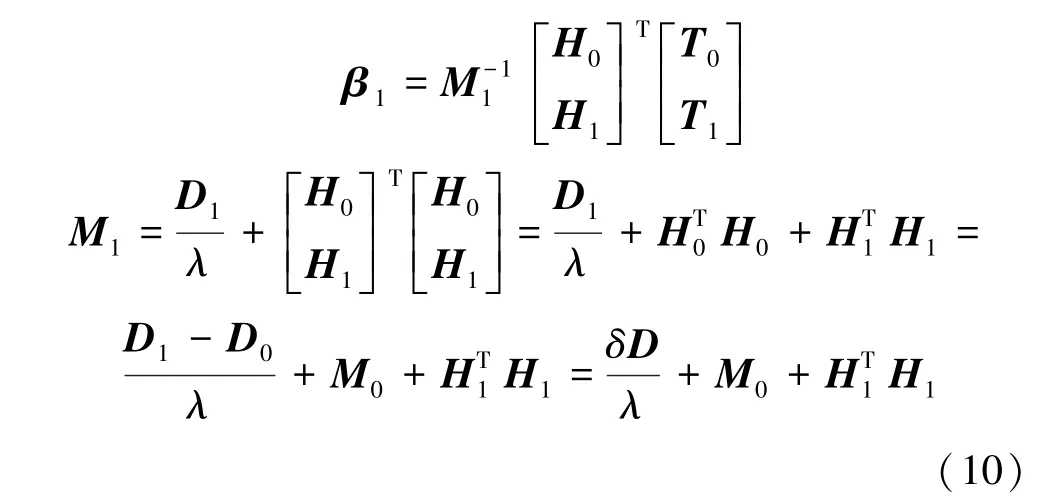
3 实验与分析

3.1 数据集

为了评估OSRVFL算法的效果，本节将提出的算法和一些已有的RVFL相关算法进行比较，选用的数据集来自于UCI机器学习存储库。使用的数据集中，随机选取数据集80%样本用作于训练集，将剩余20%的样本作为测试集。在数据被划分为训练集和测试集之前，则会将数据集的顺序重新打乱并随机选取出新的训练集和测试集。

3.2 评价指标

使用不同的统计学上的指标来对算法的性能做出评价，主要包括相关系数、均方根误差。对此拟做研究分述如下。

（1）相关系数。数学定义公式具体如下：

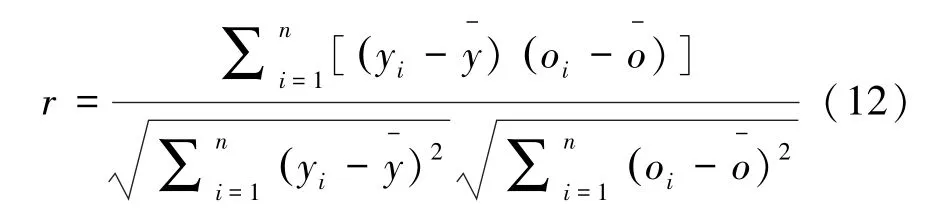
（2）均方根误差。数学定义公式具体如下：

相关系数越接近1则表示模型预测效果越好，而均方根误差衡量的是实际值和观测值之间的误差分布，取值越小，说明模型预测效果越好。

3.3 不同算法对比

表1给出了几种算法运用不同的激活函数，运行在不同的数据集上的性能比较结果。由表1中看出，对于不同的数据集而言，使用不同的激活函数能够有不同的均方根误差。

在表1基础上，确定了适用于每个数据集的最佳激活函数后，对相关系数进行了评估。研究得到的不同算法的相关系数见表2。

表1 不同激活函数结果Tab.1 Results of different active functions

表2 不同算法的相关系数Tab.2 Correlation coefficients of different algorithms

从实验结果来看，本文提出的OSRVFL方法与经典的RVFL和RVFL相比，在UCI的多个数据集中，多数情况下均取得了最佳表现。本文算法的预估值更为贴近真实值，与真实值的相关性更强。

4 结束语

针对单隐层前馈神经网络在批处理问题中，需要反复训练网络、更新权重的问题，本文将在线顺序机制与RVFL相结合，并且为了降低模型复杂度，引入了范数对输出权重进行正则化。在UCI部分分类数据集中，与另外2种同源算法进行了比较。从实验结果来看，本文提出的算法的预测表现更为出色。