基于CPG的四足机器人稳定性优化及偏航补偿

龙厚云，李 光，易 静，薛晨慷，谭薪兴，陈腾飞

（湖南工业大学 机械工程学院，湖南 株洲 412007）

0 引言

四足机器人有着高机动性和灵活性，可以适应不同地形的稳定行走。该优点可让四足机器人执行复杂地形的救援巡逻等任务。

执行任务时，可能由于运动过程中的重心不稳定会引起四足机器人的机体偏航，严重情况下甚至引起机身翻转，导致任务失败。因此四足机器人的研发中迫切需要解决重心偏移引起机体运动不稳定问题。

近年来，和四足机器人的偏航有关的研究主要集中在重心位置、偏航补偿等方面。如Lee等人为了解决四足机器人在重心偏移下trot步态的不稳定性问题，提出了一种基于遗传算法（RCGA）调节重心投影点的位置的方法。结果显示该方法可以连续、逐步地产生自适应足部运动。Wei等人为了提高四足机器人的运动性能，采用了一种对称网络拓扑结构设计的运动控制策略简化了CPG的网络结构，对四足机器人的步态规划进行稳定控制。

韩宝玲等人使用基于PSO算法调整优化四足机器人机身横向参数，优化后使四足机器人有更好的运动稳定性。易静等人分析了trot步态下机体翻转与行走偏航是由于四足机器人运动过程中机体重心偏移产生绕支撑对角线的翻转力矩以及关节摆动时产生的反作用力矩引起。

于权伟等人提出一种改进麻雀搜索算法，实验结果说明麻雀搜索算法具有高精度、收敛速度快、寻优效果明显等优点。Wang等人利用最小二乘法估计参数的指数律、对数法和复合函数模型。并进行多种拟合优度检验，得到最优的复合函数，取得了良好效果。仿真证明最小二乘法拟合函数预测的准确性和实际可行性。

本文为了减少四足机器人行走时俯仰角与偏航量，需要对CPG控制器的主要参数使用改进麻雀搜索算法进行适应性优化。在优化的基础上提出一种控制方法：用最小二乘法得出偏航函数模型预测出机体偏移量，用预测出的偏移量输入CPG的旋转步态再进行偏移量补偿。结果显示改进麻雀算法连续迭代相比原麻雀算法效果突出，对CPG运动控制模型参数优化后大大提高了机体稳定性。最小二乘法得出偏航函数可以实时控制偏航角补偿。

1 模型建立

1.1 四足机器人模型

本次研究基于宇树A1机器人，见图1。简化后的运动关节模型如图2所示，运动关节包括：连接机身、控制髋关节侧向运动的机身关节（Hip joint）；控制髋关节俯仰运动的大腿关节（Thigh joint）和控制膝关节运动的小腿关节（Calf joint）。四腿分别表示为左前腿（FL）、左后腿（RL）、右前腿（FR）和右后腿（RR）。包括足端坐标系和质心坐标系总共17个坐标系。在图2中，以右后腿（RR）坐标系为例。四足机器人具体主要参数见表1。

图1 机器人外形Fig.1 The appearance of the robot

表1 A1机器人重要参数Tab.1 Important parameters of A1

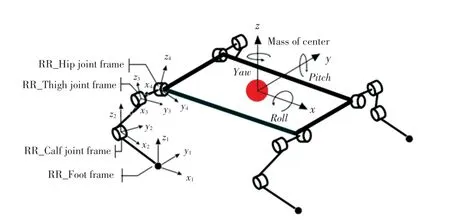
图2 机器人关节模型Fig.2 Robot joint model

1.2 CPG网络模型

四足动物普遍的行走方式是一种节律运动，通过控制每条腿相应关节的彼此协调完成运动。即按照一定的规律进行协调、控制、遵循简单规律的周期行为动作，为低级神经中枢控制的一种自激行为。仿照自然界动物的低端神经中枢模式发生器控制四足机器人运动，这便是CPG控制机理。

Hopf振荡器生成的信号的周期、幅值、收敛速度、相位等都有明确参数控制，在设计四足机器人运动网络模型时，4个全连接对称网络拓扑结构的大腿关节与足内小腿关节皆容易建立耦合相。故CPG网络模型采用Hopf振荡器作为单元模型。将四足机器人运动的控制参数引入CPG，为了协调各足间相位关系，4个大腿关节之间相耦合，每条腿的大腿关节与小腿关节构成足内耦合。CPG运动控制数学模型为公式：

其中，x，y分别为大腿、小腿关节运动信号；θ和θ分别为经过相位耦合的大腿、小腿关节运动信号；调节在摆动相频率（ω）和 支撑相频率（ω）之间的变化速度；直接控制大腿关节运动幅值；控制收敛到极限环的速度；ω为步态周期；与支撑相占运动周期的大小相关，可控制4个大腿关节间的耦合相位，生成不同的步态；A直接控制小腿关节运动幅值。

CPG运动控制模型通过调节值生成多种运动步态，如静步态（walk）、对角小跑步态（trot）、踱步态（pace）等多种运动步态。

trot步态具有较高的能效比，可以长时间保持一定的初速度，因而有非常广泛的实际用途。由游洋威的trot步态研究分析可知，trot步态存在偏航现象。本文以trot步态为例进行优化，当相位差为0.5时为trot步态，预设参数见表2，其他参数见文献［9］中生成的trot步态信号如图3所示。

表2 CPG运动模型控制参数Tab.2 CPG motion model control parameters

图3 CPG运动控制模型输出trot步态各关节信号Fig.3 CPG motion control model outputs trot gait signals for each joint

1.3 四足机器人行走实验分析

在Python环境的Pybullet仿真环境下，将CPG运动控制模型生成的trot步态信号导入四足机器人模型，取运动仿真时间为0 s与15 s时的一个步态运动周期过程图像对比，如图4、图5所示。在图4、图5中，红线为方向位移为0时的参考线。由图4与图5对比可知，0 s时参考红线在四足机器人中心，15 s时已经与参考红线有一定距离。对比表明偏航现象明显，运动过程可见机体俯仰角起伏大，四足机器人运动稳定性需要进一步提高。

图4 0 s时Pybullet仿真行走实验Fig.3 Pybullet simulation walking experiment at 0 s

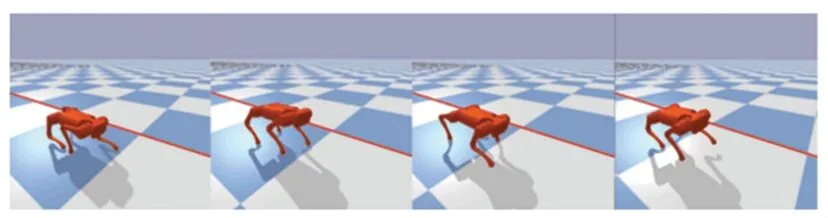
图5 15 s时Pybullet仿真行走实验Fig.4 Pybullet simulation walking experiment at 15 s

这里对行走数据变化进行分析，采集行走过程中60 s内的相关位移与姿态角数据：四足机器人在轴方向的行走位移、轴方向的距离、重心在轴的变化以及角和偏航角如图6所示。

由图6分析可知，重心起伏最大约有100 mm，角度约有6，证明机体重心起伏大、俯仰角明显。偏航角值始终有规律地增加说明机体偏离预计轨道，机身也偏离原来方位。轴方向偏移量一直稳定增长则说明每个步态周期都有重心偏移。

图6 行走实时位移与姿态角Fig.6 Real-time travel displacement and attitude angle

分析原因可知在四足机器人trot步态运动过程中，由于抬腿高度变化、重心与角起伏大等多个因素导致重心周期偏移。重心不在对角支撑线上时，重力会产生翻转力矩，导致机体运动不稳定，严重时甚至引起机体翻转。重心不在机体中心时，机体姿态会周期振荡变化，表现出绕轴偏航。

四足机器人初始生成trot步态行走稳定性较差，是因为参数基于经验预设，输出参数信号复杂，仅通过经验预设参数达不到机体稳定行走的效果。因此需要先对CPG网络模型相应主要参数进行优化，寻找出CPG运动控制模型最优参数组合。并在优化、且提升了机体运动稳定性后，再进行偏航补偿。

群优化算法应用日益广泛，如唐锴等人利用改进粒子群算法优化四足机器人机体尺寸及质心位置，Liu等人利用改进麻雀搜索算法解决了无人机路线规划问题。Jia等人利用改进麻雀算法优化深度学习机等。本文提出一种新的改进麻雀搜索算法寻找CPG运动控制模型最优参数组合以提高机体运动稳定性。在Xue等人原有麻雀算法的基础上，改进麻雀搜索算法有着较高搜索精度，全局和局部寻优能力更强。

2 改进麻雀搜索算法优化CPG参数

由上文研究可知四足机器人在行走偏航过程中，机身高度的实时变化与变化的速度都会影响机体重心位置。

2.1 基本麻雀搜索算法

麻雀搜索算法（SSA）是模拟麻雀群觅食过程中搜索食物与反捕食提出的智能优化算法。其种群有探索者、跟随者与侦查者三部分。对此拟探讨分述如下。

（1）探索者。搜索范围广，负责搜索最优值和引领种群。其位置更新公式如下：

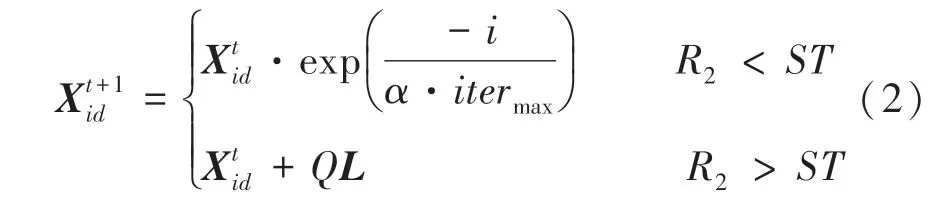
（2）跟随者。会跟随最佳适应度值的探索者来搜索最优值。跟随者的位置更新公式如下：

（3）侦查者。位置更新公式如下：

其中，为极小值；为步长控制参数；∈［-1，1］表示移动方向的随机数；f为当前麻雀个体适应度值；f为当前全局最佳适应度值；f为当前全局最差适应度值。

2.2 改进自适应权重麻雀搜索算法

惯性权重对麻雀算法搜索最优值的影响很大。在［0，1］范围内，惯性权重值大时算法全局搜索能力强，但不能在最优区域附近局部搜索最优值。惯性权重小，则搜索会陷入局部最优。算法要确保前期搜索范围广，后期局部搜索能力强。因此基于研究需要提出了一种动态非线性惯性权重公式如下：

其中，为最大迭代次数；为动态权重最大值；为动态权重最小值；为权重下降速度；为最大值与最小值持续时间。现在取20，0.9，04，075，当迭代次数为30时，权重下降如图7所示。

图7 惯性权重和迭代次数关系曲线Fig.7 Relationship curve of inertial weight and iteration times

由图7可知，迭代前期，权重衰减速度缓慢下降，有利于前期的全局搜索，快速向最优区域靠近，防止陷入局部最优；中、后期，权重快速下降，有利于搜索最优值的收敛。

2.3 仿真实验

要寻优的主要参数为：为大腿关节摆动幅度，机体每次前进距离与大腿关节摆动幅值有关，决定了处于摆动相时腾空距离；ω直接控制四足机器人的运动周期，决定各关节运动速度。并且该值会决定重心位置移动的速度；A控制小腿关节的运动幅值，决定了小腿的抬腿高度，会直接影响腾空相的时间。以上主要运动控制参数随不同环境有不同的最适应值。

仿真实验中适应度函数取决于机体传感器数据，研究选用的最佳适应度函数为：

其中，为四足机器人的行程；为不为零的极小值，以防分母为零；为四足机器人在该行程内偏航距离的最大值，加绝对值是为了防止往另一侧偏航变为负值，拉低适应值；σ为轴重心的标准差。

2.4 结果分析

麻雀搜索算法与改进麻雀搜索算法的初始种群规模皆取为20，共迭代30次。图8为优化后的四足机器人运动数据结果。

图8 改进SSA算法优化后行走实时位移与姿态角Fig.8 Real-time travel displacement and attitude angle after improved SSA algorithm optimization

改进麻雀算法寻优后主要控制参数见表3，分别取前期未优化的种群和改进麻雀搜索算法优化后的种群，对其运动稳定性进行对比，结果见表4。

表3 改进麻雀搜索算法优化后运动参数Tab.3 Improved motion parameters after SSA optimization

表4 改进麻雀算法优化后CPG控制参数值Tab.4 Improvement of CPG control parameters before and after SSA optimization

改进麻雀搜索算法优化后四足机器人主要参数可使机体稳定性增加，角度上下波动降低一倍，轴方向偏航位移减少，重心起伏大幅度降低。实验结果充分证明了改进麻雀算法对主要参数寻优的合理性和有效性。该方法极大提高了CPG运动模型的运动稳定性。

3 偏航补偿

运动控制方法的实质是控制机器人的步态，使其按照一定的轨迹行走。运动控制方法是四足机器人的核心，直接决定了机器人的运动灵活性、稳定性和地形适应性。通过四足机器人的仿真实验测试，对数据分析可以得到的增长数据与时间相关。图8中，数值波动大，但很难从理论上求得与时间的函数。故使用最小二乘法拟合出偏航角平均增长函数，对四足机器人偏航进行补偿控制。

3.1 最小二乘法拟合原理

引入一个近似的多项式函数（），使拟合值与实际值的误差的平方和最小。误差的平方和为：

在等式中：

非奇异，故方程组（8）的解存在唯一。

3.2 一阶拟合偏航控制函数

在Python环境中的科学计算库下进行矩阵运算，对原有值进行一阶拟合可以得到平均增量函数如下：

其中，为时间，（）为偏航角平均增量。这里，给出了平均增量拟合函数（）与原数据的对比曲线绘制见图9。

图9 yaw平均增量拟合函数y（t）与原yaw数据对比Fig.9 Comparison of yaw mean incremental fitting function y（t）with the original yaw data

将的平均增量导入到CPG运动控制模型对应机身旋转步态中，通过控制CPG模型的对应机身关节的运动，产生与重心偏移的翻滚力矩相反的力矩相互抵消，以此补偿产生的偏航。对应机身关节的偏航补偿函数（）为：

经过补偿函数(t)控制仿真效果数据采集如图10所示。

图10 fy函数控制行走实时位移与姿态角Fig.10 fy function controls real-time travel displacement and attitude angle

由仿真实验结果可知，重心偏移引起的偏航得到有效控制，产生的补偿合理提高了四足机器人稳定性。轴方向的偏航位移可以稳定地控制为0。通过最小二乘法拟合得到的平均增量函数，有效地解决了轴方向偏航的问题。

4 结束语

本文基于CPG运动控制模型，探讨研究四足机器人重心偏移产生的机体不稳定与偏航现象。利用改进麻雀算法优化对应参数使机体稳定性大幅度增加，并有针对性地就偏航优化问题展开研究。在此基础上对偏航角进行分析，利用最小二乘法拟合出平均函数并对偏航角度加以预测，通过对应函数对应机身关节控制来补偿偏航，仿真结果表明经过改进麻雀搜索算法优化与最小二乘法拟合函数能有效地控制偏航距离。采用该函数控制模型能够及时补偿偏航位移，使CPG运动控制模型对环境的稳定性和适应性得到了极大的提升。该方法也有一定的通用性，可用在其他步态优化与姿态角控制上。