基于地面激光雷达点云数据的森林树木分布模式提取研究

张少晴

（福州大学 数字中国研究院（福建），福州 350108）

0 引言

研究森林树木分布模式有助于了解单株树木的生长状况，利于分析树木分布规律，对掌握其过程演化、预测树木生长的变化趋势、研究森林的可持续经营具有重要意义。

一般来讲，树木在森林中的分布可以分为3种类型：随机分布、聚集分布和均匀分布。树木的空间分布模式测量方法包括样地法、无样地法、点格局分析法、分形理论。其中，样地法将样地分为若干个小样方，对小样方进行各项调查，然后用各项强度指数（如Cassie指标、丛生指数、Mrisita指数、扩散型指数等）判断分布模式的类型，使用样方法确定树木分布模式类型的结果与样方大小有关。无样地法采用最近个体法、最近相邻法、随机成对法和中心点-四分法等进行取样来分析种群的空间分布模式。点格局分析法以植物个体在空间的坐标为基本数据，每个个体被看作二维空间上的一个点，根据测定公式来研究植物种群的空间分布模式。分形理论将分形维数用于定量反映种群占据空间生态的能力，在植物种群中应用的分形维数为计盒维数。植物种群离散分布的理论模式包括Poisson分布、负二项分布、正二项分布、纽曼分布。

树木的空间分布位置是研究树木分布模式的重要基础数据，传统获取树木位置的手段不适用于面积较大的森林样地，而近年来随着地面激光雷达技术的出现就为快速、准确地获取树木高精度空间位置信息提供了可能。

因此，本文引入一种新的树木分布模式测量方法，该方法是基于地面激光雷达点云数据来获取树木的实际生长位置，用获取的高精度点云数据对树木的主干进行圆柱拟合，从而获取树木空间位置分布图，然后根据样方边界将其划分为若干子样方，以样方内树木数量的方差与均值之比作为判断树木分布模式的指标，并研究样方大小对确定树木分布模式的影响，最后对随机分布和聚集分布进行模拟，用同样的方法对其分布模式进行验证。

1 研究区

本文的实验区域位于河北省围场满族蒙古族自治县塞罕坝国家森林公园，海拔1010～1939.6 m，占地面积约为140万亩，森林覆盖率高达80%，且多为人工林，主要树种包括落叶松、樟子松、云杉、白桦等。本文共布设了2个典型落叶松样地，样地森林资产参数见表1。

表1 样地森林资产参数表Tab.1 Sample plot forest asset parameters table

2 实验方法

2.1 数据采集及处理

本文所用数据为地面激光雷达点云数据。采用Rigel VZ-400地面激光雷达获取落叶松样地的点云数据，扫描时间为2021年4月，扫描角分辨率设置为0.02°，仪器高度为1.2 m，地面激光雷达测站布设方案如图1所示，其中以0°姿态扫描45站，以90°姿态扫描8站，将整个样地分成25个30 m×30 m的子样方，在子样方的中心点、样地内部对角线上的子样方角点、样地外围的4个角点以0°姿态进行扫描，在样地的4个角点以及样地边界的中点以0°和90°姿态进行扫描。为提高多站点云之间的配准精度，扫描前在样地内树木主干的不同高度固定粘贴反射片，并保证2个测站之间能够共同扫描的反射片数量不低于8个。扫描均在无风的天气下进行，且要求树冠不能有水珠和冰晶，避免对激光雷达信号产生干扰。最后对采集的多站点云数据使用RiSCAN Pro软件进行配准、去噪等预处理工作，其中去噪误差参数值设置为15。

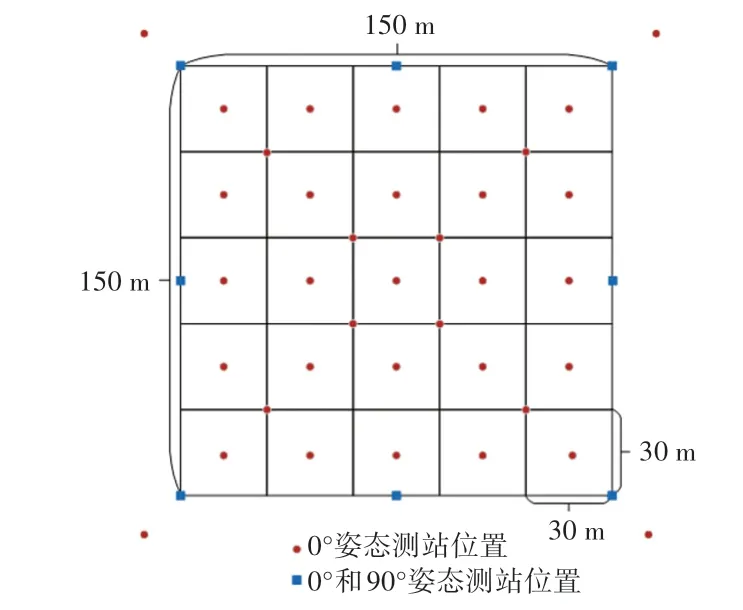
图1 地面激光雷达测站布设方案Fig.1 Layout plan of the terrestrial laser scanner

2.2 树木位置分布提取

本文研究采用霍夫变换圆拟合算法从样地点云数据中提取树木空间位置，根据样地边界，提取150 m×150 m范围的单树位置。单树位置分布图的提取流程如图2所示，主要步骤如下：

图2 树木位置提取流程Fig.2 Tree location extraction process

（1）对地面激光雷达点云数据进行地面点滤波，将其分为地面点和非地面点。

（2）将点云数据根据地面点高度归一化。使用地面点生成0.1 m×0.1 m的DEM，将所有点云数据的高度减去对应的DEM高度，即可完成点云的高度归一化处理。

（3）根据设置的高度区间，对该区间的点云使用霍夫变换进行圆检测，霍夫变换采用投票的方法，基于每个像素对自己所属的圆方程进行投票，得票数量最高的圆方程就被认为是最大概率可能存在的圆，将其圆心坐标作为提取的树木生长位置。样地1和样地2提取的树木空间位置分布图如图3所示。

图3 单株树木位置分布图Fig.3 Location map of single tree

2.3 树木分布模式分析

特定样方大小下的方差（）和均值（）之比（∶）可以用于判断森林样地树木分布模式。表2描述了与∶值相关的分布模式。当∶值等于1时，树木的分布模式为随机分布；当∶值大于1时，树木的分布模式为聚集分布；当∶值小于1时，树木的分布模式为规则分布。

表2 典型树木分布模式Tab.2 Typical tree distribution patterns

基于提取的单树位置坐标，根据预先设置的子样方数量计算∶值，并分析不同子样方大小对∶值计算结果的影响。不同子样方大小对应的∶值如图4所示。

由图4可知，样地1和样地2的∶值均小于1，因此样地1和样地2符合规则分布的树木分布模式。当子样方大小相同时，样地2的∶值均大于样地1，说明样地1的树木分布比样地2更加规则。随着子样方大小增加，样地1的∶值呈现逐渐减小的趋势，样地2的∶值先在一定的范围内上下波动后呈现增大的趋势，说明样地1的树木在整体上分布更加规则，而样地2的树木在整体分布上较局部分布的分布更趋向于随机。

图4 2个典型落叶松样地v∶m值计算结果Fig.4 Calculation results of v∶m value of two typical larix principis-rupprechtii sample plots

2.4 树木分布模式模拟

本文以几何光学模型场景的构建为基础，来模拟树木的分布模式，力求模拟的树木分布更为真实。几何光学模型由树干和树叶组成，用圆锥表示树干，用其他简单的几何体表示树叶，树叶在给定形状的冠层内随机分布且互不相交，通过设置树高、胸径、冠幅、LAI、林分密度等参数构建单株树木三维几何模型，以模拟的树木分布模式数据作为单株树木的种植位置即可模拟出基于几何光学模型的虚拟森林场景。本文用于模拟的几何光学模型参数见表3。对此拟将展开研究分述如下。

表3 几何光学模型模拟参数Tab.3 Geometrical optics model simulation parameters

（1）随机分布。根据给定的林分密度通过随机函数生成树木坐标位置，通过碰撞检测对其可种植性进行判断，最后导出树木的位置坐标即可获得树木随机分布模式数据，如图5所示。其中，模拟样地1和模拟样地2分别是根据样地1和样地2的林分密度参数模拟的树木随机分布模式，并计算不同样方大小下的∶值，如图6所示。

图5 树木随机分布模式模拟结果Fig.5 Simulation results of tree random distribution model

图6 模拟样地v∶m值计算结果Fig.6 The calculation results of v∶m value of the simulated plot

由图6可知，对于模拟的2个随机分布的样地，不同子样方大小对应的∶值均在1的附近波动，接近于随机分布模式，模拟样地1的∶值总体上大于模拟样地2的∶值，原因是对树木的可种植性进行了判断，当林分密度较大时，树木分布会略微趋向于聚集。

（2）聚集分布。树木的聚集分布模式可以用纽曼分布来模拟，Franklin等人把Neyman提出的一种描述幼虫传染性分布的方法运用到树木分布中，称为Neyman A型分布，这种分布模式假设树木首先被组合成群，组群中的树木空间分布遵循泊松过程，组群中树木的数量取决于树木的丛生程度，各组群大小分布概率由泊松分布确定，因此Neyman分布又称为双泊松分布。泊松分布方程为：

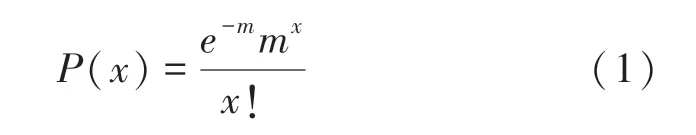
其中，是每个子样方中单树数量的平均值，（）是子样方中有棵树的概率。根据条件概率论，在一个样方中有棵树的概率（），乘以在这个样方中有个组群的概率（），就得到在给定个组群的样方中有棵树的概率。样方中有棵树的概率（）计算公式如下：

当（）和（）都由泊松分布得出后，可以得到：

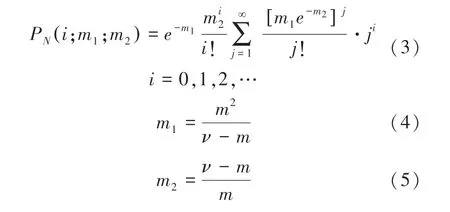
其中，表示每个样方中组群数量的平均值；表示每个组群中的树木数量；表示每个样方中树木数量的平均值；表示每个子样方中树木数量的方差。由公式（4）和公式（5）可得：，［1］，∶11

因此，由纽曼分布模拟的树木分布为聚集分布，当1时，可以模拟接近于随机分布的树木分布模式。

基于纽曼分布模拟树木分布格局的流程如图7所示，主要步骤如下：

图7 纽曼分布模拟流程Fig.7 Newman distribution simulation process

（1）输入林分密度、子样方数量、平均每个组群的树木数量。

（2）根据子样方数量，确定每一个子样方的边界。

（3）根据泊松分布模型，计算每个子样方中的组群数量。

（4）根据式（2）确定每一个子样方的树木数量。

（5）根据泊松分布模型，计算每个组群中的树木数量。

（6）根据每个子样方中的组群数量，确定组群的大小，并在子样方中随机放置每一个组群。

（7）在每一个组群中种植单树，并通过碰撞检测进行可种植性判断，当无法种植时，在该组群周围种植。

使用以上纽曼分布模拟树木聚集分布模式时，树木的聚集程度受参数的影响显著，本文根据样地1和2林分密度分别模拟4个不同聚集分布模式样地（模拟样地和）。 其中，树冠形状设置为椭球，冠幅设置为2～4 m，枝下高为8 m，树高为16～20 m。图8为各个模拟样地所对应的树木位置分布图，以及所计算的∶值。由图8可知，在林分密度和几何光学模型模拟参数相同时，越大，树木的聚集程度越明显，∶值也越大，且∶值均大于1，符合聚集分布。因此使用纽曼分布可以模拟不同程度的树木聚集效果。

图8 聚集分布模式模拟结果Fig.8 Aggregation distribution model simulation results

图9为模拟样地的∶值计算结果。从图9中可以看出，当较小时，不同的子样方大小对应的∶值在1的附近上下波动；当较大时，不同子样方大小对应的∶值均大于1。因此可以发现以下规律：当较小时，由于平均每个组群的树木数量较少，树木的聚集程度较低，树木的分布模式接近于随机分布；当较大时，由于平均每个组群的树木数量较多，树木的聚集程度较高，使用不同大小的子样方判定树木分布模式的结果均为聚集分布。

图9 模拟样地v∶m值计算结果Fig.9 The calculation results of v∶m value of the simulated plot

3 结束语

本文开展了基于地面激光雷达点云数据分析森林树木分布模式的方法研究，研究结果表明：2个典型的落叶松样地其树木空间分布模式均为规则分布；对于模拟的聚集分布样地，树木的聚集程度受大小的影响，越大，树木的聚集程度越高，当较小（1或2）时，树木的聚集程度较低，其分布模式接近于随机分布。