一种用于求解约束优化问题的改进海洋捕食者算法

2022-11-04许树辉

齐鲁工业大学学报 2022年5期

刘勇,许树辉

1.山东省冶金设计院股份有限公司,山东济南 250101； 2.齐鲁工业大学(山东省科学院) a.机械工程学院；b.山东省机械设计研究院,山东济南 250353

最优化问题普遍存在于科学工程、经济管理、国防建设、系统控制、交通规划、人工智能等各学科领域内[1]。鉴于最优化问题的重要性和普遍性,优化算法一直是科学研究的热点之一[2]。实际工程中的最优化问题中多为有约束优化问题,即要求在满足一定的约束条件的前提下,确定系统中若干变量的取值,以使系统的某个或某些指标达到最大或最小。在约束优化问题的求解中,不仅要考虑目标函数的最优,同时要考虑约束条件的满足。由于约束优化问题通常具有以下特征:目标函数是高维、多极值、不连续、不可微的；约束函数是高非线性的；可行域的形状极不规则；可行域占决策空间的比例极小；决策空间内具有多个不相连的可行域；最优解位于可行域的边界上等等,因此约束优化问题的求解通常非常困难[3]。

近年来,随着计算机技术的迅猛发展,群智能优化算法成为优化算法领域内的研究热点。相比于传统优化算法,群智能优化算法具有更强的通用性、对待求解问题本身的数学特征(如目标函数和约束函数是否可导、是否连续、是否具有凸性等)几乎没有任何要求、实现过程比较简单、对计算机硬件配置要求不高、易于被工程人员掌握等特点,因此在很多领域内迅速得到了应用和推广,基于群智能优化算法的约束优化问题的求解方法也自然引起了研究者们的广泛关注[4]。海洋捕食者算法(marine predators algorithm,MPA)是由Afshin Faramarzi等[5]于2020年提出的一种新型的群智能优化算法,该算法主要模拟了海洋环境中适者生存的自然过程,即海洋捕食者通过在莱维游走或布朗游走之间选择最佳觅食策略,思路新颖、结构简单,且在一些标准无约束优化问题的求解上表现良好,具有可预见的广泛应用前景。但同时,MPA算法在收敛速度、求解精度、稳定性等性能方面仍存在改进空间,且无法直接用于求解约束优化问题。

在基本MPA算法的基础上,通过引入一般反向学习策略和混沌局部强化搜索策略,进一步提高了算法的求解能力；通过结合ε约束法,使得算法可以有效地处理约束优化问题,之后利用13个标准约束优化测试函数检验了所设计的算法的有效性。实验表明,所设计的算法具有收敛精度高、收敛速度快、稳定性好等特点,可作为一种新的有效处理约束优化问题的工具。

1 基本海洋捕食者算法流程

作为一种群智能优化算法,MPA算法同其他群智能优化算法类似,首先进行种群的初始化。在这一阶段,算法利用式1在寻优空间内随机生成若干个候选解[5]:

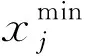
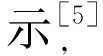
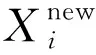
在中间三分之一阶段,算法认为对整个设计空间的全局搜索和对局部区域的精细开发同等重要,因此在这一阶段使用了两种不同的算子。解种群中一半数量的解利用式3进行更新[5],即利用莱维游走策略来实现对设计空间的全局搜索:

式中Li为一个1×D的向量,其各维均为符合莱维分布的随机数。

另一半数量的解利用式4进行更新[5],即利用布朗游走来实现对设计空间的局部开发:

式中F=(1-Niter/Nmax_iter)2·Niter/Nmax_iter,这里Niter表示当前迭代次数,Nmax_iter表示设定的算法最大迭代次数。

在最后的三分之一阶段,应主要侧重于对局部区域的精细搜索,算法采用的算子如式5所示[5],利用莱维游走来实现对设计空间的局部开发:

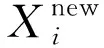
此外,算法也模拟了海洋环境中的涡流和鱼类的聚集效应,在每一次迭代中,在种群按照前述方式进行更新后,算法利用式6尝试对种群进行再一次的更新[5]。这一策略主要用于帮助算法跳出局部最优区域,缓解早熟收敛的问题。

式中r为一个在[0,1]内均匀分布的随机数；U是一个各维为0或1的1×D向量,U可按照下述方式获得:首先生成一个各维均为在[0,1]内均匀分布的随机数的1×D向量,若某维上的值小于0.2,则将其改为0,否则改为1。Xmin和Xmax分别为由各设计变量的取值下限构成的1×D向量和各设计变量的取值上限构成的1×D向量。Xr1和Xr2为在当前解种群中随机选取的两个解。

MPA的伪代码如表1所示。

表1 MPA的伪代码

2 改进海洋捕食者算法

基本MPA算法仅适用于仅对各设计变量取值范围具有限定的连续域优化问题,在处理约束优化问题时,由于需要同时考虑目标函数值的大小和约束条件是否满足,需要结合一些约束处理方法。使用ε约束法[6]来解决基本MPA算法不能直接应用于约束优化问题的求解的问题。根据文献调研[7]和[8],目前尚无将ε约束法与MPA算法相结合的研究。同时,也可通过引入一些策略进一步增强MPA算法的寻优能力。本文主要引入了基于佳点集的种群初始化策略、一般反向学习策略、混沌局部强化搜索策略来增强算法的寻优性能。

2.1 ε约束法

单目标约束优化问题的一般形式如式(7)所示[2],其中hi(X)和gi(X)分别表示等式约束条件和不等式约束条件；m1和m-m1分别为等式约束和不等式约束条件的数目。

ε约束法的核心思想是基于“约束松弛”的思想将一部分轻微违反约束(约束违反度小于ε)的不可行解视为可行解处理。对于如式(7)所示的约束优化问题,这里约束违反度的定义如式(8)所示。

在算法迭代的前期,种群中大部分解为不可行解,可行解以及约束违反度较小的不可行解的比例较小,此时为了发挥ε约束法的作用,应将ε的值设定为较大的值；而随着算法的迭代,可行解以及约束违反度较小的不可行解的比例会逐渐增加,因此在这一阶段,在衡量不同解的优劣程度时,应更侧重于对目标函数值的考虑,应将ε的值设定为较小的值。因此在ε约束法中,ε的值应随着迭代次数的增加而逐渐变小,如式(9)所示:

其中ε0表示ε的初始值,本文中取为将初始种群中各候选解按约束违反度从小到大排序后第0.2NP个候选解的约束违反度；ε(t)表示在当算法进行到第t次迭代时ε的值；Tc和β是设定的两个控制参数。然后,ε约束法利用如下三条规则来比较两个候选解的优劣:

(1)可行解始终优于不可行解；

(2)两个可行解中,目标函数值较小的解更优；

(3)两个不可行解中,约束违反度较小的解更优。

2.2 基于佳点集理论的种群初始化策略

种群初始化是MPA算法的第一步,初始种群中解的分布情况对算法最终的求解质量有很大影响[9]。在缺乏先验知识的情况下,初始种群中各解应尽可能地均匀分布在设计空间内。MPA使用随机化的方式生成初始解种群,获得的各个初始解并不能很好地分布在整个设计空间内。因此,使用基于佳点集理论的种群初始化策略代替原MPA算法中的种群随机初始化策略。基于佳点集理论的种群初始化过程如下[10-11]:

首先利用式(10)构建一个1×D的向量γ,

其中t为大于2D+3的最小素数。

然后,利用式(11)生成各个候选解。

图1给出了在二维空间内使用两种方法生成的规模均为40的种群的对比情况。不失一般性,这里两个变量的取值范围均假定为[0,1]。可见,随机法生成的解种群中的解在解空间内的分布不够均匀,解之间有聚集的情况；而基于佳点集理论生成的解种群在整个空间内分布更为均匀。同时,在设计空间和种群规模不变的情况下,基于佳点集理论生成的解的位置是固定的,这一点可增强算法的稳定性。

注:(a)随机种群；(b)佳点集种群。图1 随机生成种群与基于佳点集生成种群对比

2.3 一般反向学习策略

一般反向学习策略是文献[12]提出的一种策略。该策略的基本思想是在评估一个候选解时,同时评估该解在空间内的一般反向点,可提高找到更优解的概率。这里假设X=(x1,x2,…,xD)是D维空间内的一点,且xj∈[aj,bj],j∈1,2,…,D,则其一般反向点定义为:

一般反向学习策略的思想在很多群智能优化算法的改进中都得到了成功应用。受此启发,将该思想引入MPA的改进中。在算法每一次迭代中,以一定的概率p对当前解种群施加一般反向学习策略。具体而言,首先根据式(13)确定当前的搜索空间边界:

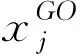
获得一般反向解种群之后,将当前解种群和其一般反向解种群构成的集合中最优的一半数量的解个体作为新的解种群进入下一代迭代。

2.4 混沌强化搜索策略

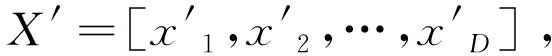
其中Xb, j表示当前种群中最优解中第j维变量的值；NFEs表示当前目标函数值评估次数；Nmax_FEs表示最大目标函数值评估次数；cj的初始值为在[0,1]内均匀分布的随机数,在算法每次迭代中,cj按照Logistic混沌映射[1]更新,如式(16)所示。

cj=4·cj·(1-cj)。

(16)

获得X′之后,对其进行评估并与当前种群中最差的解进行对比,若X′更优,则用其取代当前种群中最差的解,否则直接舍弃X′。

2.5 本文所设计的算法

在基本海洋捕食者算法的基础上,结合上述的一般反向学习策略、混沌强化搜索策略和ε约束法,构成了所设计的改进MPA算法。该算法的伪代码如表2所示。

表2 改进MPA的伪代码

3 实验结果及分析

为验证所提出的算法(IMPA-ε)的有效性,在文献[14]中给出的13个约束优化测试函数上进行了测试,并同基本MPA算法+ε约束法(MPA-ε)进行了对比。这13个测试函数在设计变量的数量、可行域在设计空间中的比例、线性不等式约束、非线性不等式约束、线性等式约束和非线性等式约束的数目、目标函数的特征等方面各不相同,可有效地检验算法的综合性能。实验中,两种算法种群规模均设置为25；最大目标函数评估次数均设为240 000。IMPA-ε中一般反向学习策略的执行概率p设为0.3；ε约束法中Tc和β分别设为2 000和5。在每个测试函数上,各算法均独立运行30次,以消除算法随机性可能带来的影响。

实验表明,对于每一个测试问题,两种算法在30次独立求解中所最终获得的最优解都是可行解,但不同算法最终获得的最优解的质量差异明显。两种算法最终获得的最优解的目标函数值的统计情况如表3所示。

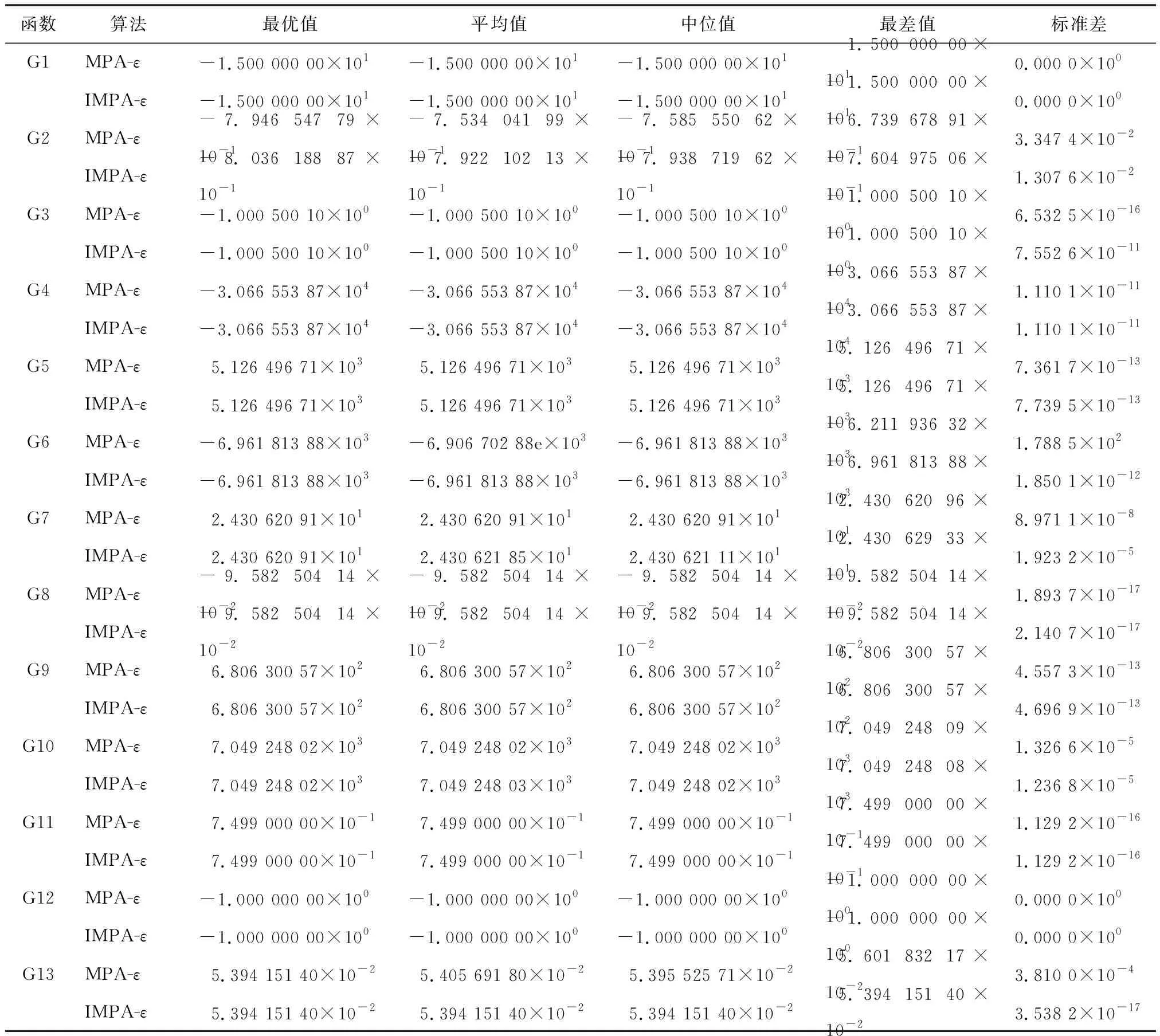
表3 MPA-ε和IMPA-ε在各问题上的获得的最优解的目标函数值的统计信息

从表3中可以看出,ε约束法可有效地辅助MPA算法处理约束优化问题。在测试的大部分函数上,采用基本MPA算法和ε约束法结合即可取得较好的寻优效果。在除G2之外的函数上,MPA-ε均找到了问题的最优解,且在大部分函数上,MPA-ε在30次求解实验中最终获得的结果均很稳定；而IMPA-ε在G2、G6、G13上的表现明显优于MPA-ε,尤其是在G2和G13上。在G2上,IMPA-ε找到了问题的理论最优解,且在各项统计指标上都优于MPA-ε；在G6和G13上,IMPA-ε的表现更为稳定；只有在G7上,IMPA-ε的表现略劣于MPA-ε；而在其它问题上,IMPA-ε和MPA-ε的表现差不多。在这13个测试函数中,G2的设计变量最多(20个),而G13等式约束条件较多、可行域较小,因此这两个问题的求解难度更大。IMPA-ε在这两个函数上表现出的性能优势更具有说服力。由此可见,在基本MPA算法中引入的基于佳点集理论的种群初始化策略、一般反向学习策略和混沌局部强化搜索策略有效提升了算法的寻优能力。