基于卷积神经网络的水中大尺寸气泡体积测定

郝宗睿,李臣豪,索铜声,陈 杰,华志励

齐鲁工业大学(山东省科学院) 海洋仪器仪表研究所,山东 青岛 266100

气液两相泡状流广泛存在于石油、新能源等领域。气泡在液相中的运动特征和形态特征是影响流场特性的重要因素,气泡的运动特征对于气液两相间的相互作用尤其是传热传质过程具有很大的影响[1]。气泡的运动特征因不同形态特征气泡的表面张力、紊动强度和粘性的不同而产生变化,进而影响水体流场的变化,气泡的形态特征作为分项流动模型的本构关系,对两相流模型的封闭有着重要影响,对于气泡尺寸的精准提取也是进行气泡形态特征描述和水体流场理论分析的基础。因此,对气泡尺寸的研究成为近些年来相关领域的研究热点[2]。

目前测量气泡特征的方法主要分为接触式测量和非接触式观测,数字图像处理技术作为非接触式的气泡观测方法广泛应用在气泡形态研究中,具有不干扰流场和气泡形态的优势[3-4]。Lecuona等[5]提出针对高密度气泡的观测,使用分水岭算法作为分割气泡的图像处理技术,但是该方法不适用于黏连性高、不规则的大体积气泡；为了适用于大气泡的识别,杜建卫等[6]提出了一种基于小波变换的边缘检测方法,该方法适用范围较广,但是准确度较低；覃若琳等[7]对分水岭算法进行了改进,一定程度上能够分割黏连气泡；胡宁宁等[8]利用卷积神经网络对大体积气泡进行识别,但是由于模型层数偏少,导致图像识别准确率较低。

本文利用旋转的半球形气泡捕获装置,使上升的小尺寸气泡在半球形装置内部聚并为大尺寸气泡,同时利用高速相机分别对小气泡和大气泡进行拍摄,利用常规图像处理方法获取小气泡的二维投影面积和等效三维体积。后基于改进的经典VGG-16卷积神经网络模型对气泡二维投影面积和对应的三维体积进行训练,通过训练后的模型计算出不规则大尺寸气泡的等效三维体积等参数,为气泡形态特征描述和水体流场理论分析提供数据支持。

1 实验装置及图像处理

1.1 实验装置

气泡模拟观测装置是以STM32单片机为控制器,以去离子水为介质,以透明的有机玻璃为观测仓,通过气体流量控制器控制气体流量,高速相机对气泡形态进行拍摄,实验装置示意图如图1所示。

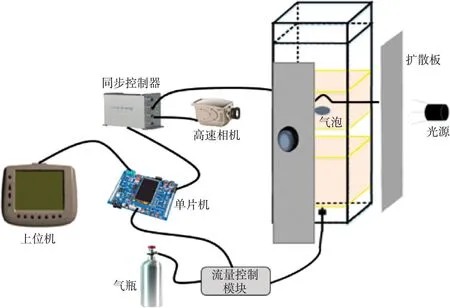
图1 实验装置示意图

气瓶中的气体以设定的流速释放,可替换喷嘴实现气泡大小的选择,获取等效直径为(2.0±0.5)mm的小尺寸气泡。实验中采用可绕旋转轴旋转的半球形气泡捕获装置,小尺寸气泡在气泡捕获装置内聚并为大尺寸气泡,当形成等效直径4.0～12.0 mm大尺寸气泡后,旋转气泡捕获装置使大气泡继续上升。高速摄像机(分辨率1 024×1 024)分别对小气泡和聚并后的大尺寸气泡的上升过程进行拍摄,获取不同体积气泡的图像。

1.2 气泡图像处理

在气泡图像的拍摄过程中,由于拍摄系统的不完善和环境的复杂性,导致图像上的干扰信息会影响有用信息的提取,采用图像处理方法对气泡图像进行处理,气泡图像处理流程如图2所示。为了去除干扰信息,首先通过中值滤波利用来自不同方向的信号所具有的空域分离性来实现信号噪声去除,去除图像中孤立像素点,避免气泡图像的灰度值跳跃[9]。为了增强气泡边界等有用信息,降低气泡图像背景信息的干扰,对气泡图像进行图像增强,将增强后的气泡图像设定像素阈值实现气泡图像的二值化。最后利用Sobel算子对经过处理后的气泡图像进行边缘检测,将气泡的边缘信息提取出来,为气泡的二维投影面积和对应的三维体积的获取提供数据支持。

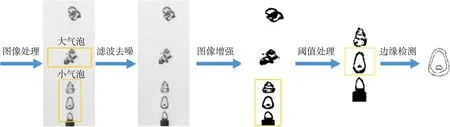
图2 图像处理流程图

2 卷积神经网络的模型建立及训练

2.1 网络模型的建立

气泡二维投影面积和三维体积的计算对图像识别精度有相对较高的要求,由于卷积神经网络相较于其它网络模型具有局部感受和参数共享等特征,可以精准的对图像的局部特征进行识别提取[10-11]。经典卷积神经网络VGGNet模型通过3×3的小卷积核进行多次的卷积池化操作,使模型获得很好的感受野,具有较高的图像识别精度,但是由于模型中的全连接层的每个神经单元都与上一层的神经单元连接,使得全连接层的权值参数较多,导致含有三层全连接层的经典VGG-16模型所占计算机资源较大,运算效率较低[12-13]。为了解决VGGNet模型运算效率较低的问题,对VGGNet模型进行改进,改进网络模型如图3所示,将VGG-16模型的全连接层层数缩减为一层,模型所占内存显著降低,可在确保识别精度的同时维持较高的运算效率。

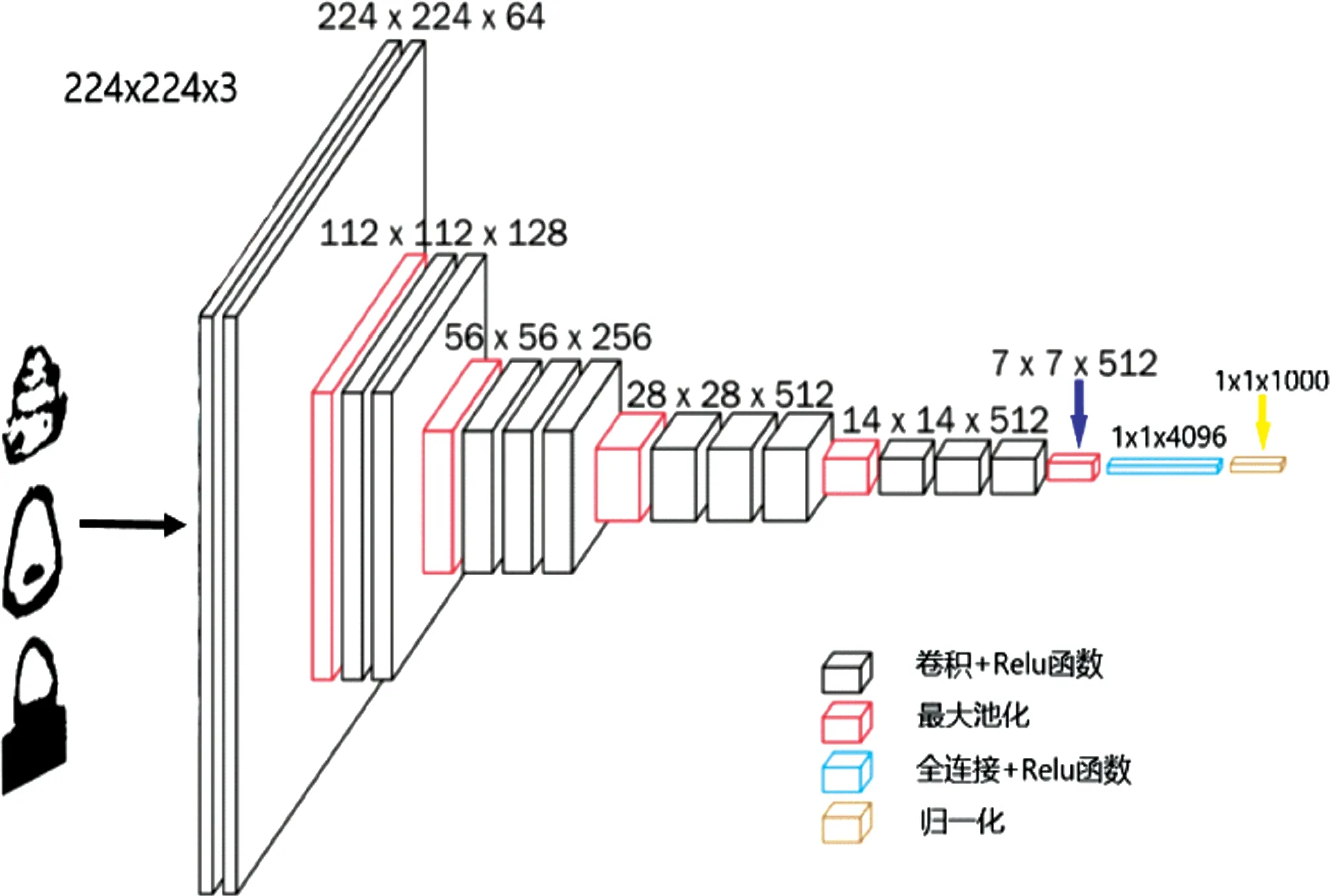
图3 改进型VGG-16网络模型

2.2 数据集的引入

卷积神经网络模型的训练需要提供足够量的训练样本,所以需要建立气泡的二维投影面积和对应的三维体积的样本集。首先,对小气泡进行一系列常规的图像处理操作后,计算气泡连通区域内的像素点数,根据高速相机的分辨率计算出每个像素点的面积,进一步推算出目标气泡的二维投影面积。其次根据等效体积公式(1),获取气泡的等效体积:

式(1)中,Vx表示推算的气泡等效体积；Sx表示第x张气泡图像投影面积；V表示实验获取的气泡体积；n表示气泡上升过程中包含的图片张数。根据获取的气泡二维投影面积和三维体积数据建立对应的训练样本集。

通过数据扩增技术将200组训练样本集经旋转平移方式扩充为6 000组。由图4可知,相比于目前流行的ImageNet20数据集,MNIST数据集的过拟合比率可稳定在0.95～1.05,可有效的避免后期的训练过程中的过拟合问题的发生。所以采用Pytorch中的MNIST数据集将扩充的6 000组样本引入为初始数据集合,为后续的模型的训练提供数据集。

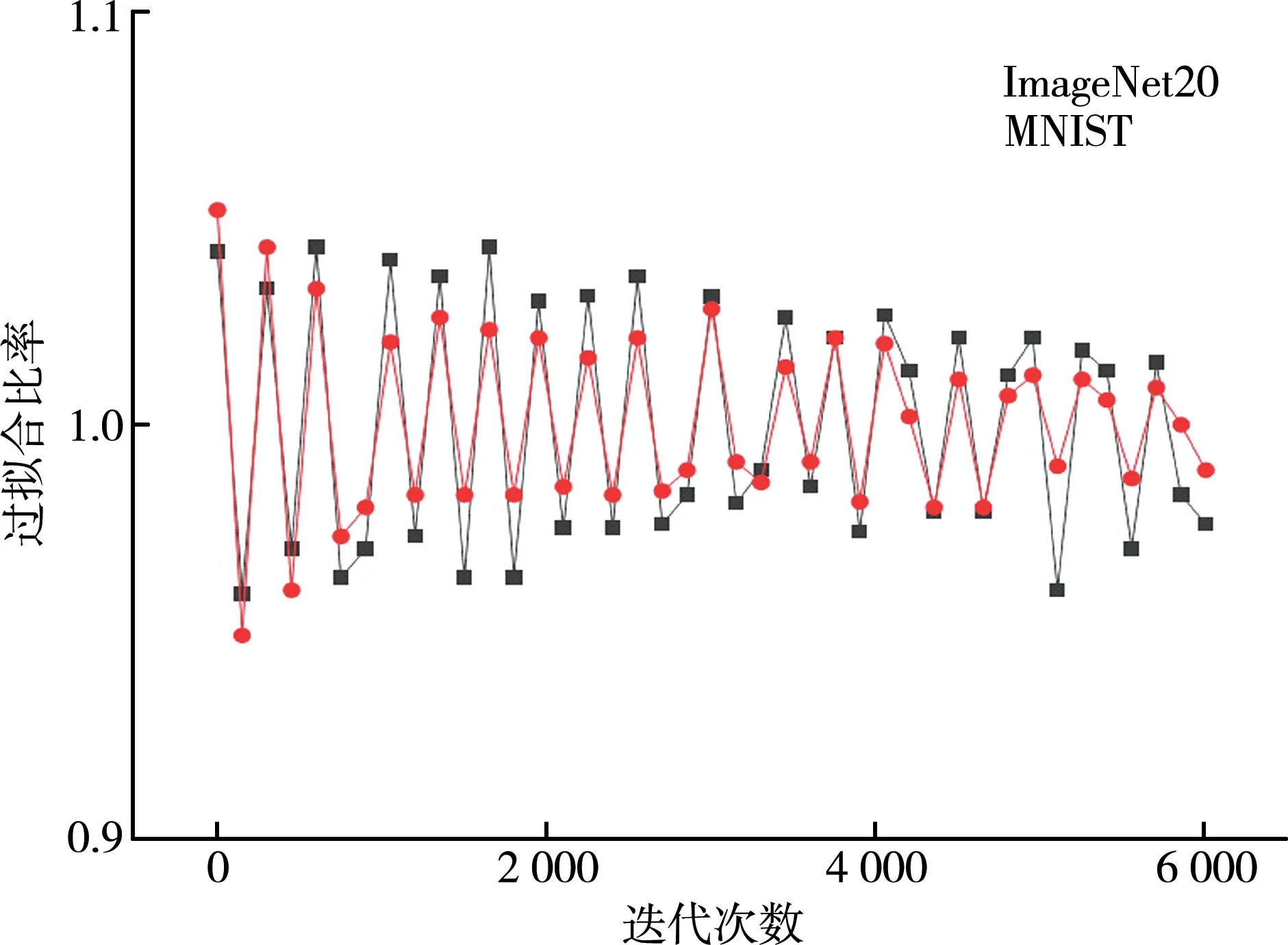
图4 不同数据集下的过拟合比率

2.3 模型的训练

将建立的的气泡数据集输入到改进的网络模型中,利用softmax分类函数和交叉嫡损失函数输出预测结果,并对预测结果的误差进行计算。经多次反向传播训练,得出最优的预测结果和最低的实验误差,模型训练流程如图5所示。

图5 模型训练流程

首先将数据扩增后的数据集输入到模型中,利用softmax分类函数对模型输出结果进行归一化处理,计算出每种预测结果出现的概率。通过Softmax分类函数对n种可能出现的结果的概率预测公式如式(2)所示[14-15]:

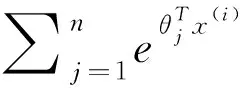
式(3)中,L(θ)表示损失值；z表示训练样本集的容量；y表示真实值与预测值的对应性；λ表示输出结果之间的影响系数；l{y(i)=j}∈{0,1}表示当计算结果的预测值与真实值一致时该值取1,否则取0。

局部感受和权值共享是卷积神经网络中最重要的两个特点,这种特点既维持了图像识别的局部针对性,又提高了网络数据的共享性,模型的有效训练是对局部感受和权值共享的进一步校正。对卷积神经网络模型的训练可以很好的检验模型对气泡形态特征预测的准确率和预测误差,实现网络模型与气泡图像特征高精度识别的需求相适应。

2.4 模型的评估

为了验证训练后卷积神经网络模型的可行性和准确性,通过Python对改进后的经典VGG-16卷积神经网络模型进行仿真实验,得出模型对气泡图像预测的损失值和准确率。

由图6可知,训练初始阶段,loss值从较高值急剧下降,在500次迭代之后,loss值随着训练轮数的增加而缓慢下降,最终趋于收敛。在收敛过程中,loss值多次出现了大幅度震荡变化情况,这是由于训练设定的学习率过大导致的,但是样本数据量充分,模型经过多次论证实验,训练的轮数足够多,通过适当降低训练的学习率,模型最终达到了收敛状态。

图6 模训练的损失值 图7 改进模型与经典模型的准确率对比

为了验证改进后网络模型的识别准确率是否符合预期要求,利用Python分别对经典VGG-16模型和经典网络改进模型的准确率进行仿真实验,准确率计算结果如图7所示,对比发现经典VGG-16模型在1 000次迭代内呈现出相对较高的准确率,但是在迭代次数超过1 000次以后,准确率增速变缓,最终在迭代3 000次左右达到准确率的峰值97.63%。相比之下改进的卷积神经网络模型初始响应略慢,但是只需要迭代1 800次即可达到98.87%的准确率峰值,耗时更短,准确率更高。

3 实验分析

由于较小尺寸气泡的形变量较小,可以将其等效为球体或者椭球体,根据等效体积公式获取相对精准的气泡体积。但是当气泡的雷诺数(Re)大于500时,气泡形状会呈现出不规律的变化,使得按照公式计算的气泡三维体积与实际体积存在偏差。

为了降低计算偏差,引入卷积神经网络对气泡图像进行训练识别,利用经过大量训练的模型对不规则大尺寸气泡进行识别预测,获取大气泡等效直径的预测值；将小气泡的体积叠加等效为聚并之后的大气泡体积,反向推导体积公式,获取等效直径的实验值。通过图8对比发现可知,在直径为4～6 mm的气泡中,预测结果与实验结果的偏差在±8%左右,分析原因是由于气泡尺寸较小,对于气泡的预处理深度不够,造成网络模型对气泡图像识别难度增大；在直径为6～12 mm的气泡中,预测结果和实验结果的偏差有效的控制在±8%以内,误差的存在是由于随着气泡的增大,图像识别难度降低,但是更加不规则的形变导致二维投影的面积无法真实反应出气泡的三维体积。

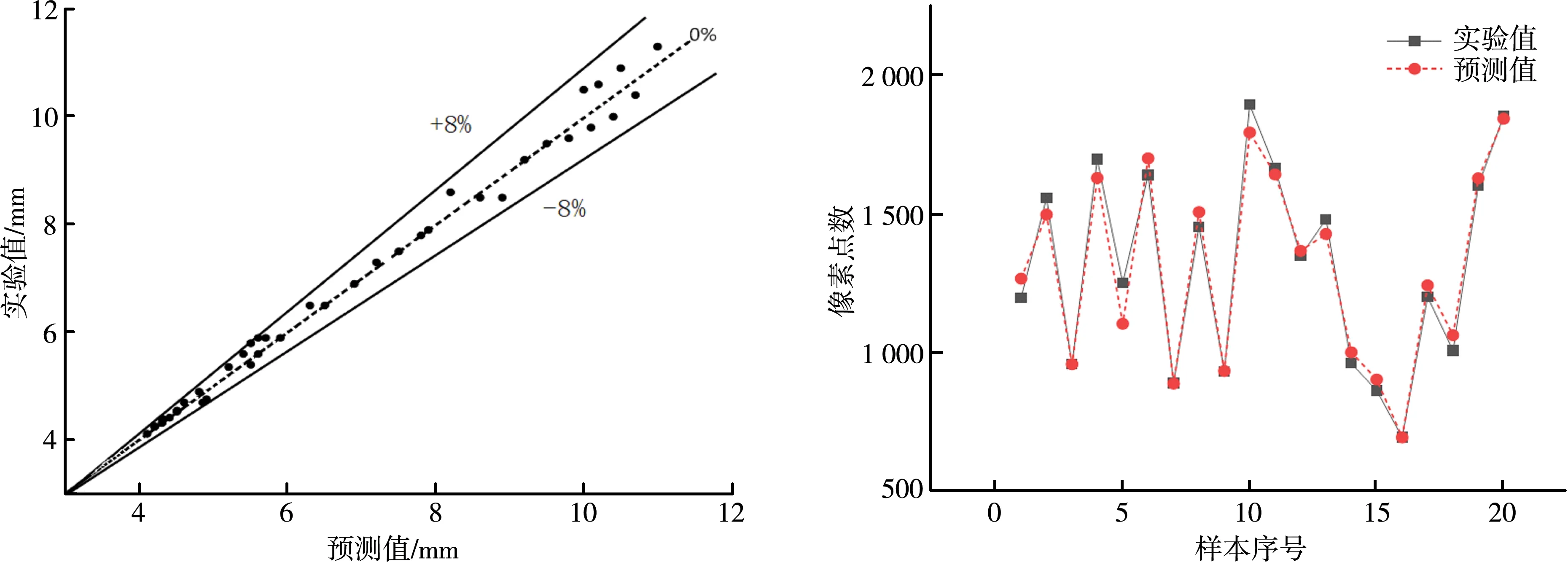
图8 气泡直径预测值和实验值相对误差 图9 气泡面积预测值和实验值的对比

为了确保等效直径提取的准确性,对气泡二维投影面积的预测值和实验值进行对比。由于使用的高速相机分辨率为1 024×1 024,以此推算出每个像素点的面积,可根据像素点的个数获取气泡的二维投影面积。网络模型对抽取的实验样本的气泡像素点个数进行识别检测,对比分析人工处理得出的像素点个数,对比结果如图9所示,二维投影面积的预测值和实验值最大误差小于5.20%,满足研究预期要求。

采用卷积神经网络模型对抽取的实验样本中不规则大气泡的体积进行识别预测,与通过小气泡体积叠加推算出的大气泡体积的实验值对比,由图10可知,网络模型对体积小于200 mm3的中型气泡体积识别准确度较高,预估的气泡体积平均误差为3.13%；对于200～450 mm3的大尺寸气泡,预估的体积平均误差为5.24%。这主要是由于本网络模型的训练样本缺少较大气泡的样本集,导致网络模型对较大气泡体积的预测产生细微偏差；其次是大尺寸气泡不规则的形变,导致根据气泡二维投影面积无法有效的推算出形状多变的三维体积。

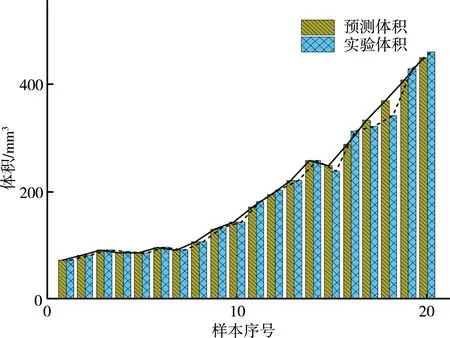
图10 气泡体积预测值和实验值的对比

4 结 论

通过气泡捕获装置获取气泡图像,经过图像预处理后,利用训练后的卷积神经网络模型对发生不规则形变的大尺寸气泡的三维体积进行预测。通过对比发现,本文所改进的网络模型对气泡等效直径的预测误差小于±8%,对气泡二维投影面积的预测误差小于5.20%,对气泡三维体积的预测误差保持在5.24%以内,相比于通过传统的图像处理后,再进行三维体积假设的方法,具有操作方法简单、预测精度高、计算速度快、可靠性高的优点。但是随着气泡尺寸不断的增大,网络模型对气泡的预测准确度有所下降,后期考虑通过增大气泡训练样本的尺寸区间,对网络模型进行更大气泡尺寸范围的训练,来降低对大尺寸气泡三维体积预测的误差。