一种未知环境下方向自适应的机器人避障算法

2022-11-04陈振国任维康桂方燚田晓丹卢瑞芳

华北科技学院学报 2022年5期

陈振国，任维康，桂方燚，田晓丹，卢瑞芳

(华北科技学院计算机学院，北京东燕郊 065201)

0 引言

智能化的移动机器人应用愈加广泛，与之相关的各类技术研究也逐渐成为热点，其中，自主避障技术是机器人实现自主移动的关键，这一方面需要灵敏精确的传感器实时的收集和表达障碍物的位置，另一方面需要科学有效的路径规划方法指导机器人安全的穿过障碍区域。路径规划分为全局路径规划和局部路径规划[1-3]，前者多用于已知的障碍物环境中，但机器人工作环境相对复杂，单一的全局静态路径规划满足不了实际要求，面对动态的障碍物环境，需要配合使用有效的局部避障算法[4]，许多学者针对此问题做了深入的研究和改进。王宏伟等[5]为了提高无人机的避障效率，在速度障碍法的基础上建立动态障碍物的冲突模型，将避障问题转化成数学问题，通过求取最优解的方式，避免无人机与动态障碍物的碰撞；张贺等[6]将速度斥力场融入人工势场算法，为了避免动态障碍物的斥力驱使机器人偏离正常航向，以障碍物的移动信息生成速度斥力，引导机器人从障碍物后方同行，能够解决在机器人动态避障时避障路径过长，避障方向不佳的问题；Zhang等[7]基于无人水下航行器不确定性的动态工作环境提出了一种基于碰撞风险评估和改进速度障碍法的动态避碰方法，首先根据障碍物与无人水下航行器的最小相遇时间和最小距离建立碰撞风险评估模型，筛选关键障碍物以避免碰撞，再基于改进的速度障碍法建立了优化目标函数，在速度空间中获取最佳避障速度做最终达到避障的目的。王宏伟和张贺等人研究结果都能在一定程度上提高机器人在动态障碍物环境下的避障能力，但没有考虑机器人和障碍物尺寸对路径选择造成的影响，不适用于障碍物复杂的场景，代婉玉等[8]针对此问题基于TEB(Time Elastic Band)算法研究复杂动态环境中的避障，对障碍物进行膨胀处理且对障碍物周围的区域分级处理，通过危险距离对机器人的速度加以限制，提高了机器人的复杂动态环境中运行的平滑性和安全性，但同时会出现安全区域过大的问题，导致整体规划的路径过长。张晓晔等[9]基于电力巡检机器人进行研究，构建时间栅格地图对区域内动态障碍物和静态障碍物进行标识，以最优搜索算法规划全局路径，再以人工势场法[10]作为局部避障的支撑，有效的避免了局部死锁，同时提高了躲避动态障碍物的效率；王洪斌等[11]提出一种A*和DWA算法融合的混合算法，首先使用自适应圆弧算法优化了全局路径规划转折角多且角度大的问题，并且同时规划到多个目标点的平滑路径，针对路径上的动态障碍物，提出基于预瞄偏差角追踪动态目标的方法，对DWA算法进行了改进，弥补了A* 算法时效性差的缺陷，能够避开动态障碍物的同时，结合全局地图规划出最优路径。二者为了保证整体最优在避障时引入了全局路径搜索算法，这类方法更加适用于已知环境例如工厂或仓库场景，在机器人工作的多数未知环境下此类方法无法完成全局规划，并且算法融合会产生计算量大、局部冲突等问题。

本文结合以上研究，针对未知环境提出一种动态窗口法的改进方法，首先针对原算法会经常绕过障碍物稠密区域的问题改进动态窗口，根据障碍物间距优先选择与终点连线夹角最近的区域，并设置临时目标点，在安全的基础上保证了全局最优，与此同时检测可能出现的动态障碍物，获取动态障碍物的尺寸、速度和距离信息，生成并实时更新轨迹交叉点，融合相关信息自适应调整速度方向，最终机器人完成避障的同时，能够提高整体的路径规划效率。

1 传统动态窗口法

动态窗口法[12]由Fox等人在曲率速度法的基础上提出，算法首先需要建立机器人的运动模型，然后根据障碍物的位置合理的规划线速度和角速度，基于此速度组就可生成预轨迹，也就是所谓的动态窗口，最后设定评价函数对生成的轨迹组进行评分获取最优预轨迹，指导机器人完成运动。

1.1 设置速度采样空间

首先机器人自身拥有极限大小速度，设为Vf(v，w)，其中v为线速度，w为角速度，该速度满足：

Vf={(v,ω)|vmin≤v≤vmax,ωmin≤ω≤ωmax}

(1)

其次机器人的动力决定其加速度大小，因此可将一段时间内速度集合约束为Vs，其中当前线速度为vs，当前角速度为ωs，时间间隔为t，则当前Vs(v,w)速度空间为：

(2)

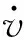
(3)

式中，dist(v,ω)表示速度(v,ω)生成的轨迹离障碍物的最小距离。结合机器人的自身机械性能，最终速度采样空间定义为Vr(v,ω)，Vr受机器人极限速度Vf(v,ω)和最大避障速度Ve(v,ω)限制，并且在生成一次动态窗口的时间内，速度应满足Vs(v,w)，因此Vr(v,ω)为三者的交集，即：

Vr=Vf∩Vs∩Ve

(4)

1.2 轨迹的生成和评价

基于设定的速度与加速度的组合(vi,wi)和时间周期t，将t分为n段Δt模拟周期内的移动就能生成一组轨迹，轨迹生成后，通过评价函数进行评分，从中选取得分最高的路径下发给机器人执行，评价函数一般表示为：

G(v,w)=α·H(v,w)+β·D(v,w)+γ·V(v,w)

(5)

G(v,w)代表函数输出，即为最优速度组合，H(v,w)用来评价轨迹和机器人与目标点连线的角度差D(v,w)用来评价轨迹中机器人与障碍物的距离，评价没有障碍物采样路径时设定该函数为一个常数，V(v,w)对采样轨迹的速度进行评价，α、β、γ代表函数项的权重。

最后为了保证得到平滑轨迹，还需要对函数项进行归一化处理，处理方法是各项除以各项的总和，如下：

(6)

其中，n为采样的所有轨迹；i为待评价的当前轨迹。

2 改进的动态窗口法

2.1 基于临时目标点的最优方向选取

在静态障碍物空间，原算法存在处理某些稠密障碍物空间时效率不高的问题，如图1所示，具体表现为路径规划会限于局部最优或者直接绕过区域，造成总路程增加，一般的解决方法为将DWA与全局路径规划融合[11]，此类方法一方面增加计算量的同时缺乏实时性，另一方面在处理未知的静态障碍物环境时会失去作用，本文针对此问题提出临时目标点机制，对动态窗口法做了改进。

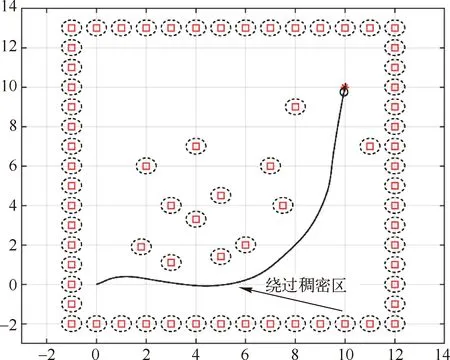
图1 绕过稠密区

首先使用传感器获取前方障碍物信息，包括障碍物的数量、存在的角度和障碍物的间距，以此判断是否属于稠密区域，如图2所示，在XOY区域内存在A、B、C、D和E五个障碍物，外围虚线作为障碍物的膨胀危险空间以控制间距，膨胀距离设定为机器人的半径，空间区域表示即将发生碰撞，不建议机器人进入该区域，其中B、C、E构成一个相对稠密的障碍物空间，机器人从O点出发向目标点G行进，从图中可知，α、β、γ、ε和η角覆盖的区域为可通行区域，θ1、θ2、θ3和θ4角覆盖的区域不宜行驶。

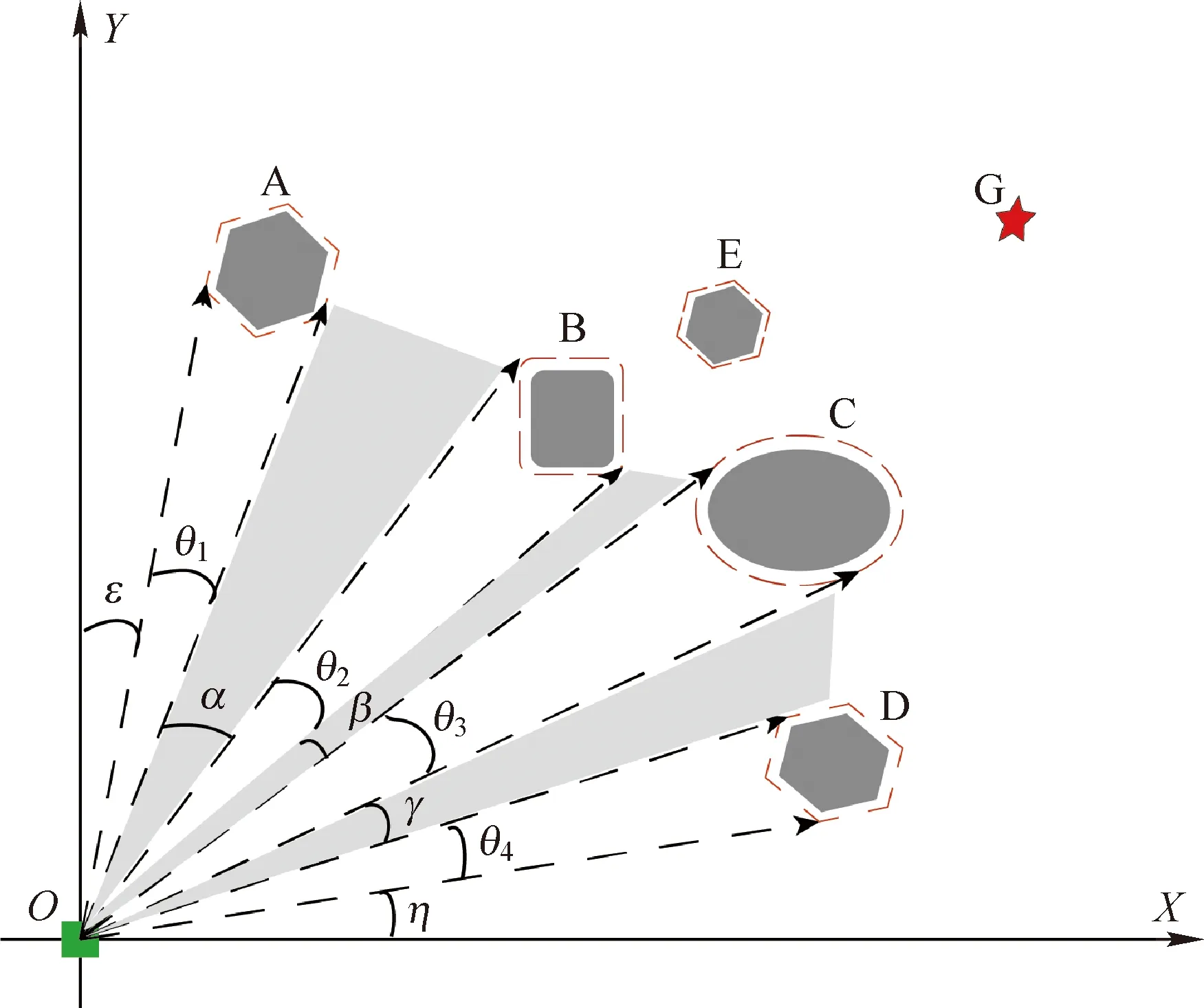
图2 稠密区通行角度示意图

机器人使用原算法在通过类似障碍物区域会因为评价函数失灵出现两种异常状态，一方面距离评价子函数权重过大会导致避开最优可通行区域而去选择其他通行区域，另一方面如果为了保障角度最优而单一的降低距离评价子函数的权重不仅会造成局部最优还可能会造成碰撞，此时借助相关障碍物探测传感器将可通行区域跟机器人与目标点连线的夹角比对，易知将预轨迹规划在α、β、γ角区域比其他区域能够更快的到达目标点，并且从β角区域行驶去往目标点的距离最近，但该区域较窄需要精确计算能否通行。此时通过传感器可以轻易获得机器人与障碍物某点之间的距离，以及相邻两个障碍物之间的夹角大小，又已知余弦定理推导式：

(7)

即可以根据此公式计算B、C两障碍物膨胀后的间距，若大于机器人直径，则以B、C连线中点为临时目标点，临时目标点的方向即为当前环境下DWA算法最优的路径规划方向。此临时目标点的物理意义为当前环境下在全局最优的基础上辅助机器人以最快的速度和安全的状态向最终目标点行驶，并且由于设置了较窄的角度区域，此方法可以有效减少迭代过程中的计算。

2.2 动态障碍物的处理方法

为了更加符合实际环境，动态障碍物基于图2的静态障碍物空间研究处理，通过对比相邻次数的传感器扫描信息，可获知动态障碍物的存在，此时如果使用原算法的评价函数应对，不仅不能达到较好的避障效果，还可能造成路线挤兑使机器人偏离最佳航向甚至与其他障碍物相撞，本文针对此问题，在处理动态障碍物的问题上，提出基于交叉危险区的自适应阈值触发机制。

如图3所示，在XOY区域内，机器人通过稠密区向目标点行驶，传感器检测到场景内存在移动的障碍物Z，动态障碍物作为环境中的移动元素，不会始终处于机器人的路径上，所以为了提高效率，在检测到环境内存在动态障碍物时，使动态窗口计算先不考虑障碍物Z，同时对动态障碍物的信息实时监测，包括实时更新机器人与障碍物之间的距离，以及通过一定的移动距离计算其平均速度，计算可知，障碍物前进方向与机器人规划的前进轨迹交叉点为R，并在行进间根据障碍物Z的线速度方向和角速度实时更新交叉点R的位置。

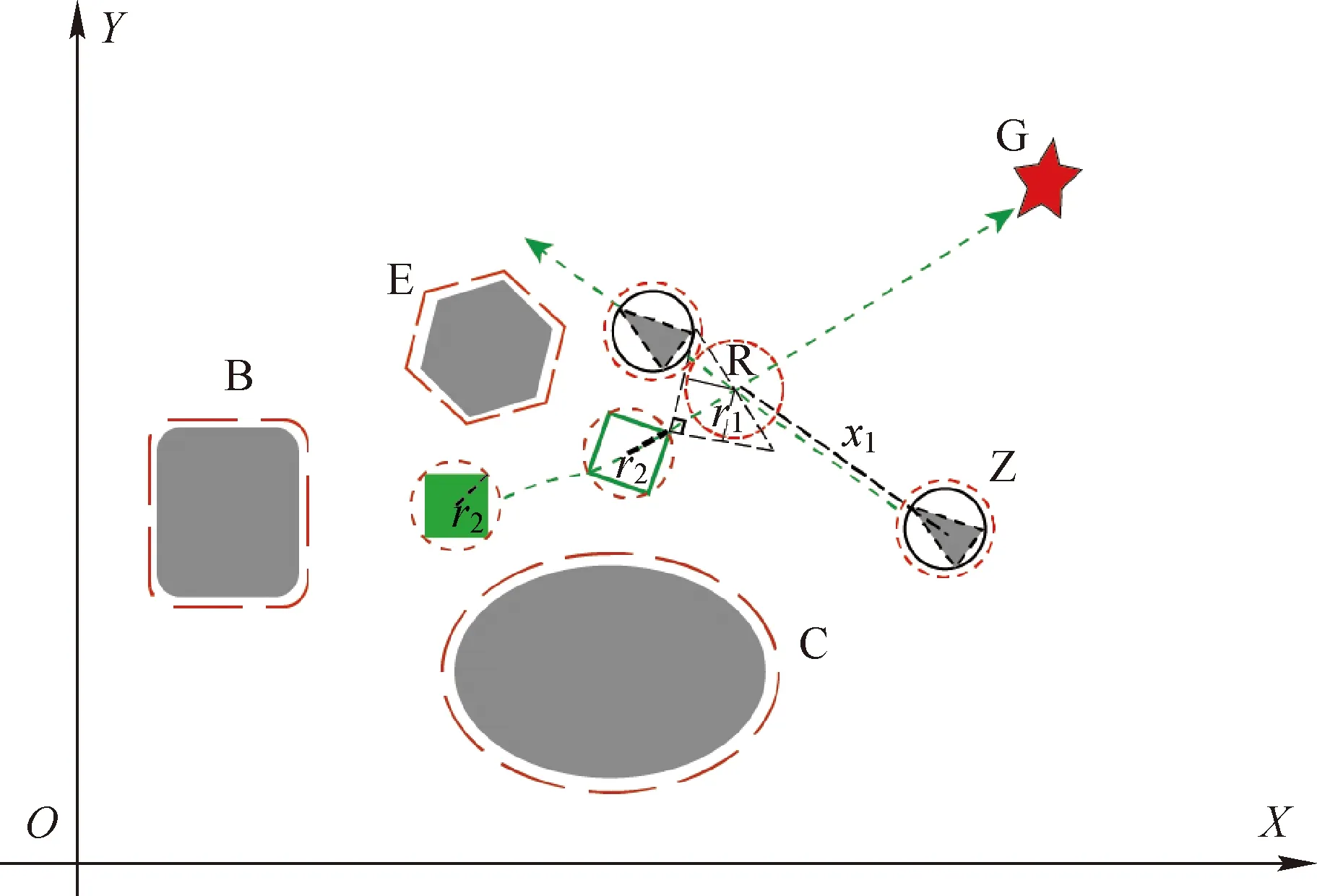
图3 动态障碍物场景

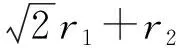
情况一：机器人行驶距离x2时障碍物Z已经先通过危险区，或者

(8)

即障碍物Z能够先通过危险区，此时评价子函数S(v,w)决策结果为按照原算法规划的路径行驶。

情况二：到达距离x2时障碍物没有到达危险区，此时若

(9)

即机器人可以先于障碍物Z完全通过危险区，此时决策结果同情况一。

情况三：机器人或障碍物Z能先到达危险区但通过时会相撞，即

(10)

或

(11)

此时两者都离危险区较近，可以把危险区作为静态障碍物使用原算法处理，如图4所示。

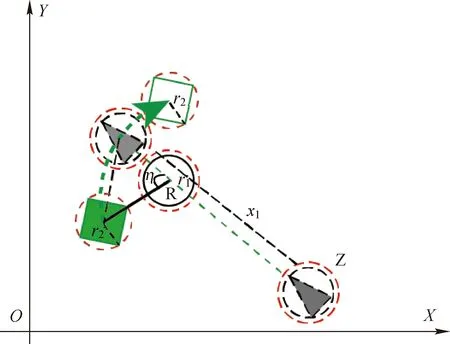
图4 情况三处理方法示意图

当机器人速度满足：

(12)

即危险区作为静态障碍物处理时，机器人能在障碍物Z开始离开危险区之前从障碍物前方绕过危险区，评价子函数S(v,w)决策结果为剔除向右的预轨迹，机器人基于原算法从危险区左侧绕过。如果不能满足公式(12)，那么再结合公式(10)可以判定障碍物Z已经完全进入危险区并但没有完全离开，那么评价子函数S(v,w)决策结果为机器人基于原算法从危险区右侧绕过。

最后的改进算法公式为：

G(v,w)=α·H(v,w)+β·D(v,w)+γ·V(v,w)+φ·S(v,w)

(13)

在遇到动态障碍物且触发阈值后，系数φ权重最大，即由轨迹决策子函数S(v,w)优先决定轨迹方向，阈值触发机制在一定限度内提高了算法的路径规划效率，使机器人安全处理动态障碍物的同时降低偏离最佳航路的概率，使机器人的运行尽量不受环境内动态元素的影响。

2.3 改进算法的处理流程

改进后的算法流程如下：

(1) 进入未知动态区域，扫描区域内的障碍物信息，判断是否有稠密复杂区域，若有稠密障碍区域，则确定与目标点连线夹角最近的可通行区域a以及临时目标点；

(2) 获取机器人目前的角速度和线速度状态，基于原算法计算然后筛选出区域a方向的动态窗口(v,w)，生成最优轨迹并下发行驶指令，同时检测区域内是否有动态障碍物，循环这一过程；

(3) 如果过程中检测到动态障碍物，先按照预定路线行驶，并实时对障碍物的信息进行监测，生成且不断更新危险区；

(4) 机器人行驶到既定距离时，触发评价子函数S(v,w)，融合机器人和已有的障碍物信息预测下一步机器人与障碍物之间的相对位置，基于计算结果打分，保留较优方向的动态窗口；

(5) 把最终选择的轨迹方向下发给机器人，继续行驶并循环这一过程直至到达目标点。

算法一次迭代流程图如图5所示。

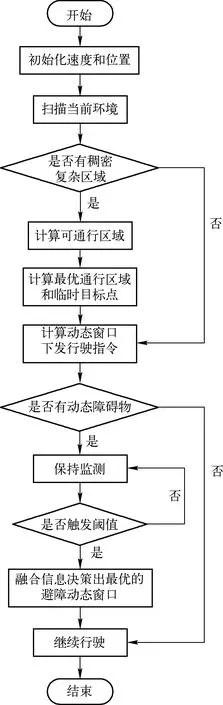
图5 算法流程图

3 仿真及结果分析

本文基于MATLAB R2021b来验证改进思路的可行性，首先介绍实验相关参数和环境信息，本文设定在一段封闭未知的13×15栅格区域，区域内包含稠密障碍物区和动态障碍物，机器人起点设置为(0,0)，终点为(10,10)，障碍物膨胀后统一为半径0.4 m的圆，机器人半径为0.2 m，静态障碍物为正方形，动态障碍物为菱形，相关具体参数见表1～3。

表1 机器人运动学模型

表2 DWA路径规划算法参数

表3 DWA算法评价函数参数权重

首先构建静态障碍物地图测试算法处理稠密区域的效率，如图6所示，与图1相比，改进后的算法能够避免评价函数失灵的情况发生，精确的判断由(2,2)，(3,1)，(3,4)，(4,3)组成的稠密区域的障碍物间距，选的较优且安全的航向夹角行驶。

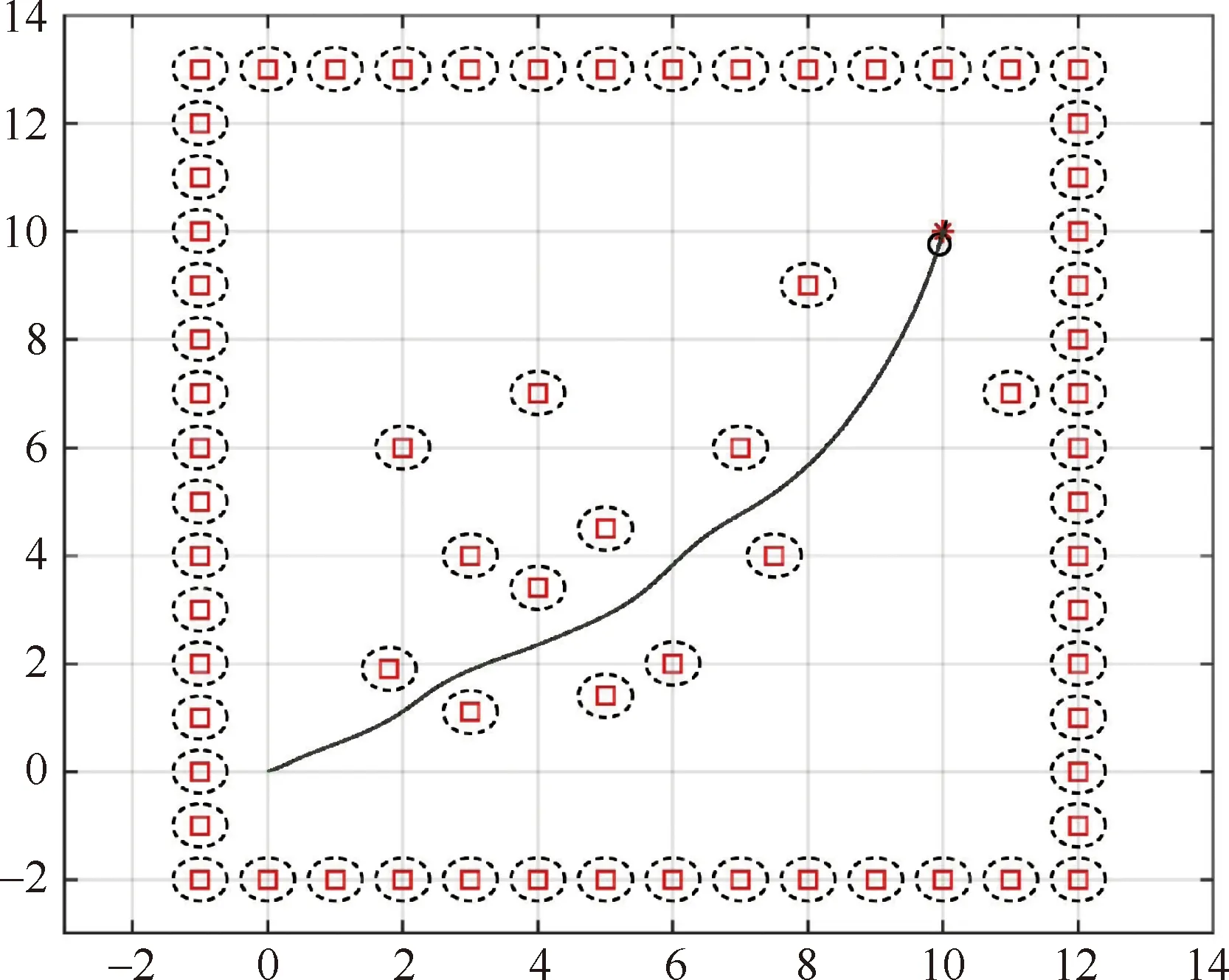
图6 改进DWA算法穿过稠密区效果

完成静态层面的处理后，为了验证面对动态障碍物时的处理思想，在静态地图的基础上添加三个移动的障碍物，如图7所示，传统的动态窗口算法遇到动态障碍物处理效率不高，避障效果随机，容易发生路线挤兑造成碰撞。

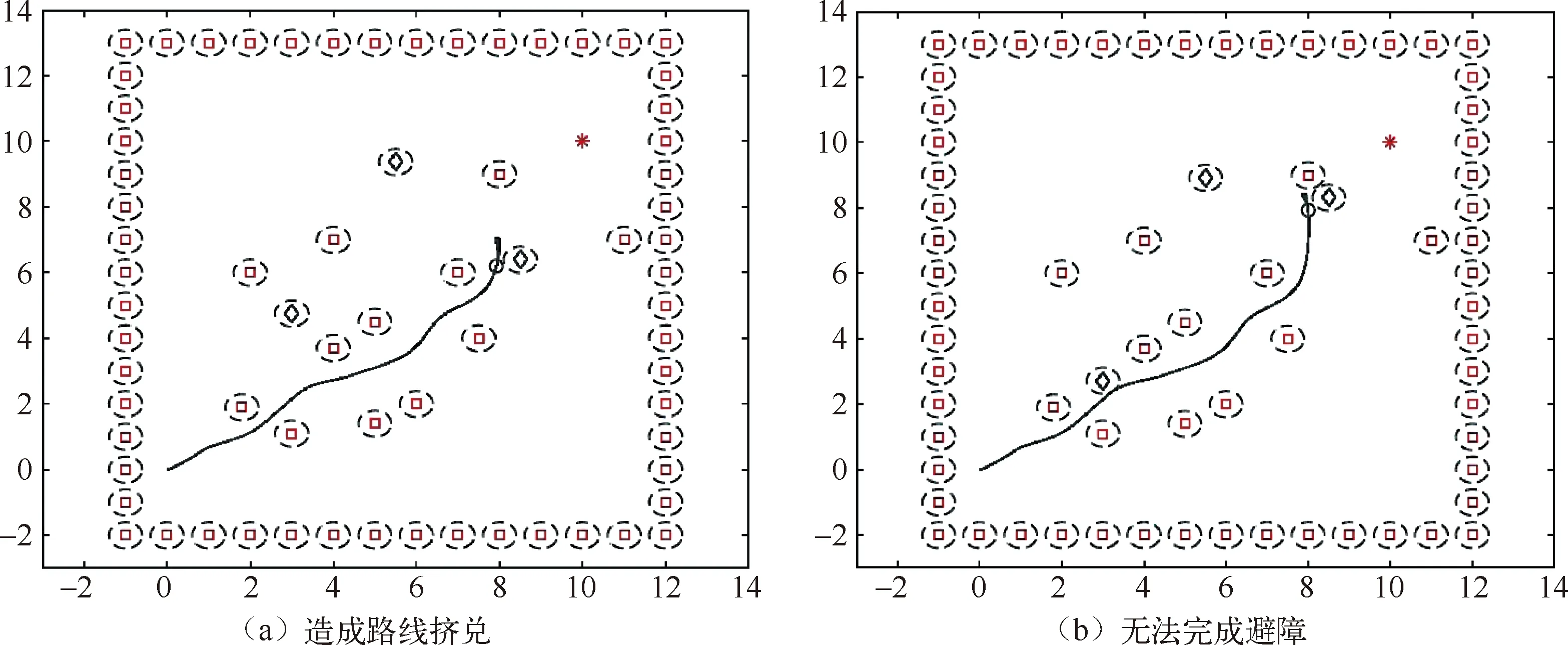
图7 原算法处理动态障碍物的表现

一方面，原算法在面对动态障碍物时为了避开障碍物需要一直计算新的动态窗口，这无疑增加了算法对计算资源的耗费；另一方面原算法在绕路的同时不能融合动态障碍物以及周围环境信息，评价指数失灵，造成了“为了避障而避障”的现象。本文结合这两个关键具体问题作为改进点，改进效果如图8所示。

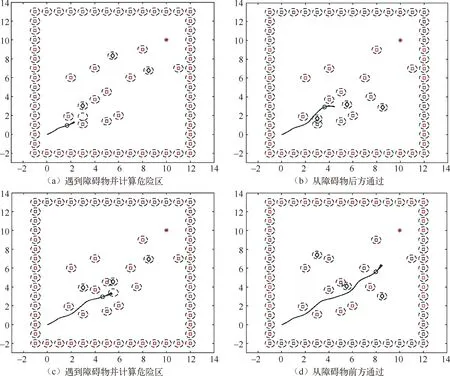
图8 改进算法处理动态障碍物的表现

图8(a)和(b)中机器人检测到动态障碍物并实时计算轨迹交叉区域，并且障碍物会先到达交叉区域，最后从障碍物后方安全避开障碍物，图8(c)和(d)中，障碍物速度较慢，机器人可以先于障碍物完全通过危险区，评价函数决策为按照原规划路径行驶，从障碍物前方完成避障，减少了不必要的计算，保证了机器人的最佳行驶方向，本文对改进前后算法各仿真实验30次，实验数据定量比较见表4。

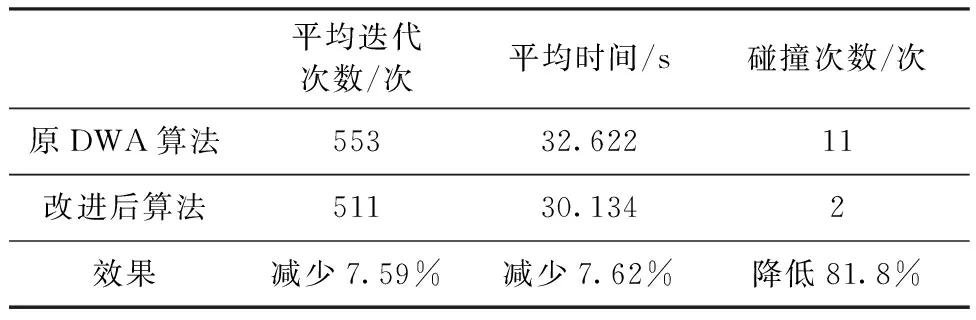
表4 DWA算法优化前后定量对比

通过以上实验，验证了本文的改进思路，改进算法能够达成机器人在未知环境下自适应选择方向的原始目标，使机器人通过复杂区域的安全性有效提高，主要体现在机器人处理稠密障碍物场景时基于该算法可以快速确定当前场景下的最佳行驶方向，同时，基于传感器监测动态障碍物信息并实时更新，在机器人安全避开动态障碍物的前提下仍然可以计算出较优的行驶轨迹。