基于模态平均曲率差归一化的桥梁结构损伤识别

肖 冰,祝可为

(福建船政交通职业学院 土木工程学院，福建 福州 350007)

0 引言

结构损伤识别是桥梁健康监测的一个重要环节，即对桥梁结构的静、动态特征、表面形态、尺寸大小等参数进行检测，进而研判桥梁结构的健康状态, 分析损伤程度和位置，评估剩余寿命，判定交通控制及维修决策等[1]。桥梁结构损伤识别技术的发展大致可划分为三个阶段：第一阶段是专家主观诊断法。以行业专家的理论知识和经验对诊断信息做出判断，适合简单的桥梁类型。第二阶段是传感器优化布置和动态测试方法。依据分析模型进行信号处理和优化算法，已在工程中推广应用。第三阶段是智能诊断技术阶段。为了满足大型复杂结构的健康诊断要求,智能诊断技术主要以知识处理为核心,数据处理、信号处理与知识处理相融合[2]。近年来，行业学者对此相继开展研究。杨波教授研究团队提出了一种以多分辨率的小波分析作为识别和定位损伤的方法，该方法对土木工程结构损伤在线检测奠定了基础[3]；李爱群等以润扬大桥悬索桥为依托背景，利用主成分分析方法，建立模态频率环境条件的归一化方法, 进行长期结构损伤监测，得到的实际损伤与预测损伤基本一致[4-5]；宗周红教授提出了基于响应面的桥梁有限元模型修正方法,包括试验设计、参数筛选、响应面模型选择以及模型检验等，具有较好的优越性[6]。经过长期研究，虽然在桥梁结构损伤识别领域已经发展了大量的研究方法，但基于模态曲率差的损伤诊断与寿命预测方法鲜见报道。曲率模态是一种比较理想的损伤检测方法，反映结构局部特征变化的模态参数，可以有效解决结构损伤分布和损伤程度的随机性、振动源不明确性、振动测试环境不可控性等复杂问题[7]。

基于此，本文采用模态平均曲率差归一化的损伤识别指标，在前人研究成果上，提出“归一化位移均值波形的平均曲率差法”( 即“归一化AD波形的平均曲率差法”)和“归一化位移方差波形的平均曲率差法”(即“归一化DV波形的平均曲率差”)两种损伤定位方法。通过简支梁推导出指标的有效性，进一步应用于悬索桥钢箱梁损伤识别。利用模型算例中主梁不同部位单损伤和双损伤的四种损伤工况，验证指标的有效性、准确性和鲁棒性。

1 基本理论

1.1 归一化位移均值波形的平均曲率差法

根据多自由度体系模态原理，位移向量可按振型贡献进行展开。

(1)

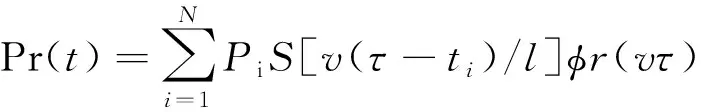
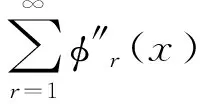
由公式(1)可知，位移的曲率与振型模态相关，结构损伤会改变各阶振型模态，位移曲率也会发生变化。振型模态是轴向位置x的函数，由此用位移曲率来定位结构损伤具有可行性。在实际工程应用中，很难得到精确的模态振型，高阶振型更难获得，且测得的模态振型误差较大[8]。相对而言，位移测量更为直接，且精度也越来越高。利用中心差分法的原理，得出推导公式(2)。

(2)

式中，i表示测量结点编号；Δ表示相邻测点之间的间距。

由公式(2)可知，各测点的曲率是时间的函数，与外界激励有关。用不同时刻的测点曲率差值无法准确进行损伤定位，需要另寻指标，使其不受外界激励的影响。位移振型叠加中qr(t)在数值上与振型的参与系数一致，而振型参与系数与结构形式有关，不同结构形式，决定振动位移的模态阶数也不相同。在不同的外界激励下，各振型对振动位移的参与系数略有改变，但基本保持相同的比重[9]。因此，荷载作用时间内的位移平均值会使重要参与振型的比重放大，而高阶参与系数较小的振型将被减弱。在位移两次差分后，这种关系依然存在。据此推理，本文提出了利用位移均值来作为损伤评判的特征参数，表达式见公式(3)。

(3)

式中，N为采样点数，由采样频率和荷载作用时间决定，即N·T·H，H为采样频率；ADi表示第i个结点位置的位移均值。将所有测量结点的位移均值连成曲线，由相邻结点的位移均值经过差分即可求得曲率。

将一段时间内各测点的位移均值连成曲线构成波形，称为“位移均值波形”，简称“AD波形”。结构局部发生损伤后，损伤位置附近测点的振动位移均值将发生变化，AD波形也同样发生变化。只是由于在低损伤状态下，变化量值较小，无法直观观察。根据中心差分法求解AD波形各结点的曲率，将损伤引起的变化量放大。表达式如下：

(4)

式中,Ci是位移均值在i结点处的曲率；ADi表示第i个结点位置的位移均值；Δ为相邻结点间的距离。

1.1.1 归一化处理及损伤定位

归一化处理的目的是为了减弱或消除外界不同激励的影响，使结构运营阶段任意时间段内的AD波形曲率具有可比性[10]。以简支梁为例，归一化处理过程为：

(5)

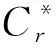
将公式(5)代入公式(4)求解各测点的AD波形曲率再进行归一化，发现归一化后位移均值的曲率与外界荷载无关，且基本不受荷载移动速度的影响。因此，归一化处理能消除不同外界激励的影响，可进一步用于损伤定位分析。

结构未发生损伤时，对多个激励样本分别进行求解，将样本分为两组，代入公式(5)得到判断结构损伤与否的“归一化位移均值波形的平均曲率差”阀值T。结构发生局部损伤后，取多个损伤结构的样本，重复上述步骤，得到损伤识别指标DIi，再进行损伤定位。

(6)

式中,Δδt,i和Δδt,j的数学期望值为0，Δεt在结构损伤前后会发生明显的跳跃。

1.1.2 抗噪性能分析

实际工程应用时，振动响应信号中噪声和测量误差是不可避免的，因此有必要讨论基于“归一化位移均值波形的平均曲率差”损伤定位方法的鲁棒性。用u(x,ti)表示x结点在ti时刻的位移响应，用αδj表示高斯白噪声，且δj为相互独立的。噪声幅值α则与信号采集设备有关，通常被认为是一个定值，带噪声的位移响应公式如下：

(7)

由此可见，取平均值后，噪声所占的比重得到有效的降低，且采样数量N越大，噪声的影响就越小。但位移均值的有效成分保持不变。噪声对曲率的影响：

(8)

由公式(8)可以看出，对有噪声的 AD 波形求曲率后，AD 波形曲率的噪声水平与位移均值的噪声水平相当，即曲率值没有放大噪声的影响，说明“归一化位移均值波形的平均曲率差法”具有较好的抗噪性能。

1.2 归一化位移方差波形的平均曲率差法

方差是各个数据分别与其和的平均数之差的平方的和的平均数，在概率论和数理统计中，方差(Variance)用来度量随机变量和其数学期望(即均值)之间的偏离程度。

(9)

初始位置对位移方差计算没有影响，在任意激励下，多自由度体系若处于完好状态，各测点的位移振动响应离散程度变化是一致的。当体系发生局部损伤时，局部位置振动响应的离散程度将会发生变化。这种变化仅从单个点是无法看出，但利用相邻结点的离散程度，通过曲率可以将微小的变化放大。因此，引入位移方差波形曲率的平均差来进行损伤定位，简称为“DV波形曲率”，得到位移方差波形曲率：

(10)

式中，Ci是位移方差在i结点处的曲率；DVi表示第i个结点位置的位移方差；Δ为相邻结点间的距离。

1.2.1 归一化处理及损伤定位

同样以简支梁推导可知，归一化后位移方差的曲率与外界荷载无关。因此，归一化处理能消除不同激励对位移方差曲率的影响，具有工程应用前景。先确定未损伤结构的损伤指标阀值T，再对比损伤结构计算的归一化DV波形的平均曲率差，以此来判断结构损伤的位置。

1.2.2 抗噪性能分析

检验“归一化位移方差波形的平均曲率差”损伤定位方法的抗噪性能直接关系其工程应用价值。考虑添加噪声αδj后的位移方差表示为：

DVnoise=D[u(x,t)]+D[αδj]=DV+D[αδj]

(11)

当用于求解方差的振动位移数据量越大，各测点信号中噪声的方差相差越小。公式(11)噪声引起的曲率接近于零。由此说明，位移方差曲率具有一定的抗噪性能，结构损伤前后的“归一化位移方差波形的平均曲率差”可以消除噪声的影响。

2 算例

2.1 工程简介

本文以福建某自锚式悬索桥作为研究对象，大桥由引桥和主桥组成，主桥全长 470 m。悬索桥结构指标见表1。

表1 悬索桥结构指标表

悬索桥的主塔刚度较大，局部的轻微损伤不会引起主梁竖向振动频率的变化。因此，本文对主梁损伤进行识别。

2.2 数值模型

用MATLAB软件随机生成车重和车间距，形成1600辆车的荷载模型，车辆分布总长度达到 26 km。结构损伤前后均以此荷载模型加载，假设以 80 km/h的速度经过主桥，需要20分钟。因此，损伤前后任意选取10分钟数据用于计算位移均值曲率。车重及车辆分布如图2所示。

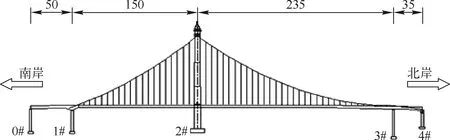
图 1 悬索桥整体布置图

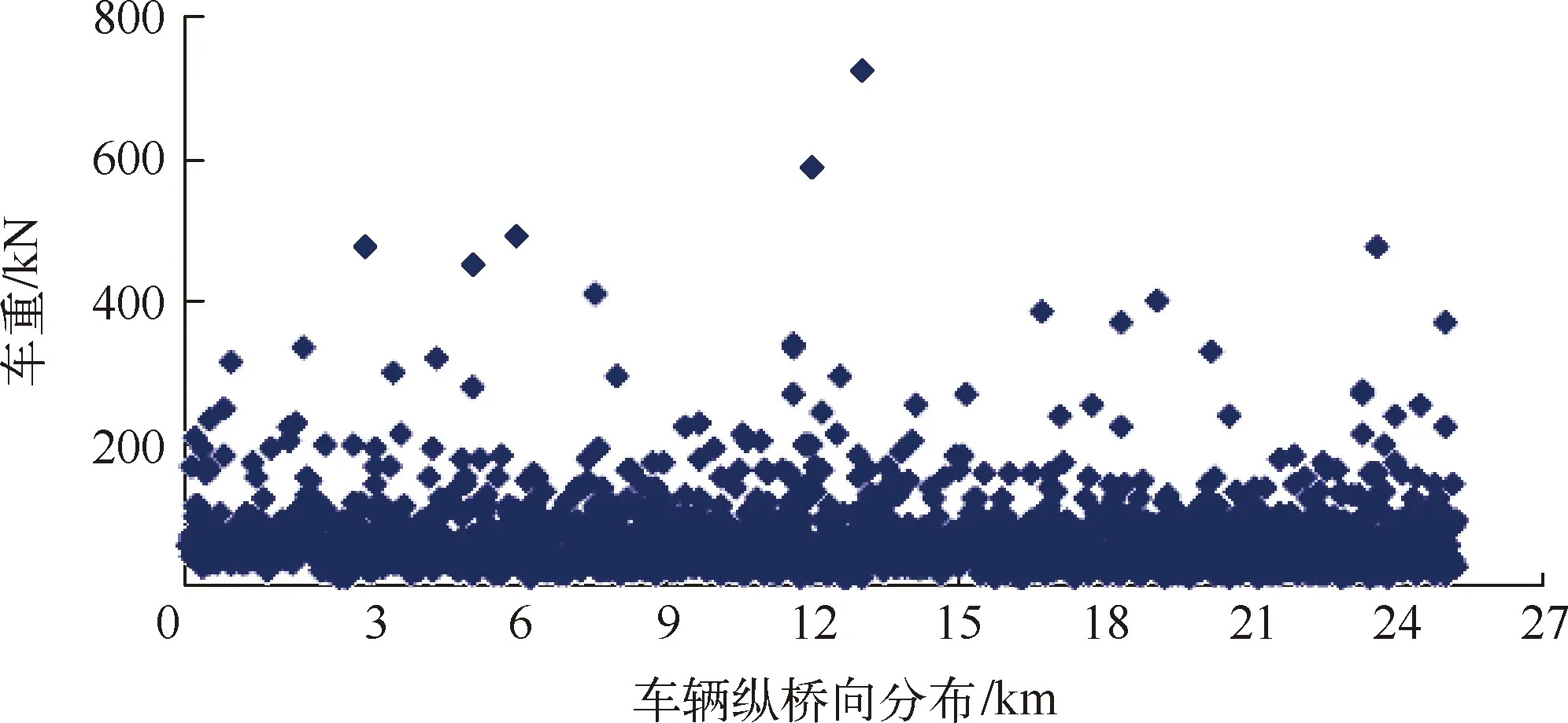
图 2 随机车重及车辆荷载分布

用有限元软件SAP2000建立随机车辆荷载模型，设置频率50 Hz。模型中以横隔板间距3.5 m 为一个单元，一次进行编号。考虑悬索桥结构吊索对主梁刚度的影响，吊索之间主梁中点的刚度与吊索结点位置刚度相差较大，将严重影响曲率计算结果，因此文中以吊索所在位置处主梁结点的位移响应为分析对象。模型中各分析结点的编号如图3所示。

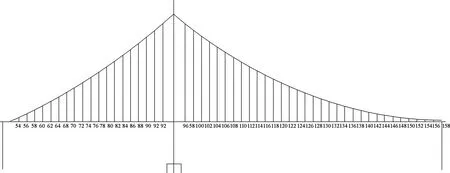
图3 悬索桥主梁结点和单元编号

2.3 损伤识别分析

结构损伤的模拟通常采用刚度折减来模拟，损伤单元的刚度为(EI)D=x(EI)，x为刚度折减系数，(1-x)为损伤程度。考虑悬索桥在实际工程中发生多种损伤，对主梁数值模拟4种工况，各工况的损伤通过降低弹性模量来实现，损伤程度为20%，损伤情况分为单点损伤(126单元、104单元)及双点损伤(106单元和118单元、126单元和140单元)，各工况见表2。假设桥梁易损截面发生损伤，模拟塔梁连接处截面，主跨跨中附近截面的损伤。

表2 自锚式悬索桥的模拟损伤工况

2.3.1 归一化位移均值波形的平均曲率差法(简称“AD 波形法”)

所有工况均采用与损伤单元相近的15个结点数据进行分析，考虑实际测量中频率的噪声水平，分析了添加1%和5%噪声水平后的损伤识别情况。损伤定位的阀值计算也由相同的结点集来确定,得出归一化位移均值波形的平均曲率差法测定的损伤定位识别结果。

图4(a)～7(a)分别为各工况主梁各节段完好状态下损伤识别指标阀值，从图中可知，添加1%和5%噪声水平后，平均曲率差阀值统一确定为0.04。图4(b)～7(b)分别为各工况下主梁各节段损伤定位结果，即各测点的损伤判别因子值。由于损伤判别因子值为曲率指标，所以对两个边界点不能进行计算，但对于边单元依然具有识别效果，因此两边界范围内即为损伤点。单损伤工况下，图4中124单元～128单元发生了突变，容易识别出范围内对应的结点126单元为损伤单元；图5中102单元～106单元发生了突变，容易识别出范围内对应的结点104单元为损伤单元；双损伤工况下，图6中104单元～108单元，116单元～120单元均发生了突变，容易识别出范围内对应的结点106单元、118单元为损伤单元；图7 中124单元～128单元，138单元～142单元均发生了突变，容易识别出范围内对应的结点126单元、140单元为损伤单元。因此，在任意损伤情况下，归一化位移均值波形的平均曲率差法均能有效准确得定位出自锚式悬索桥的主梁损伤。

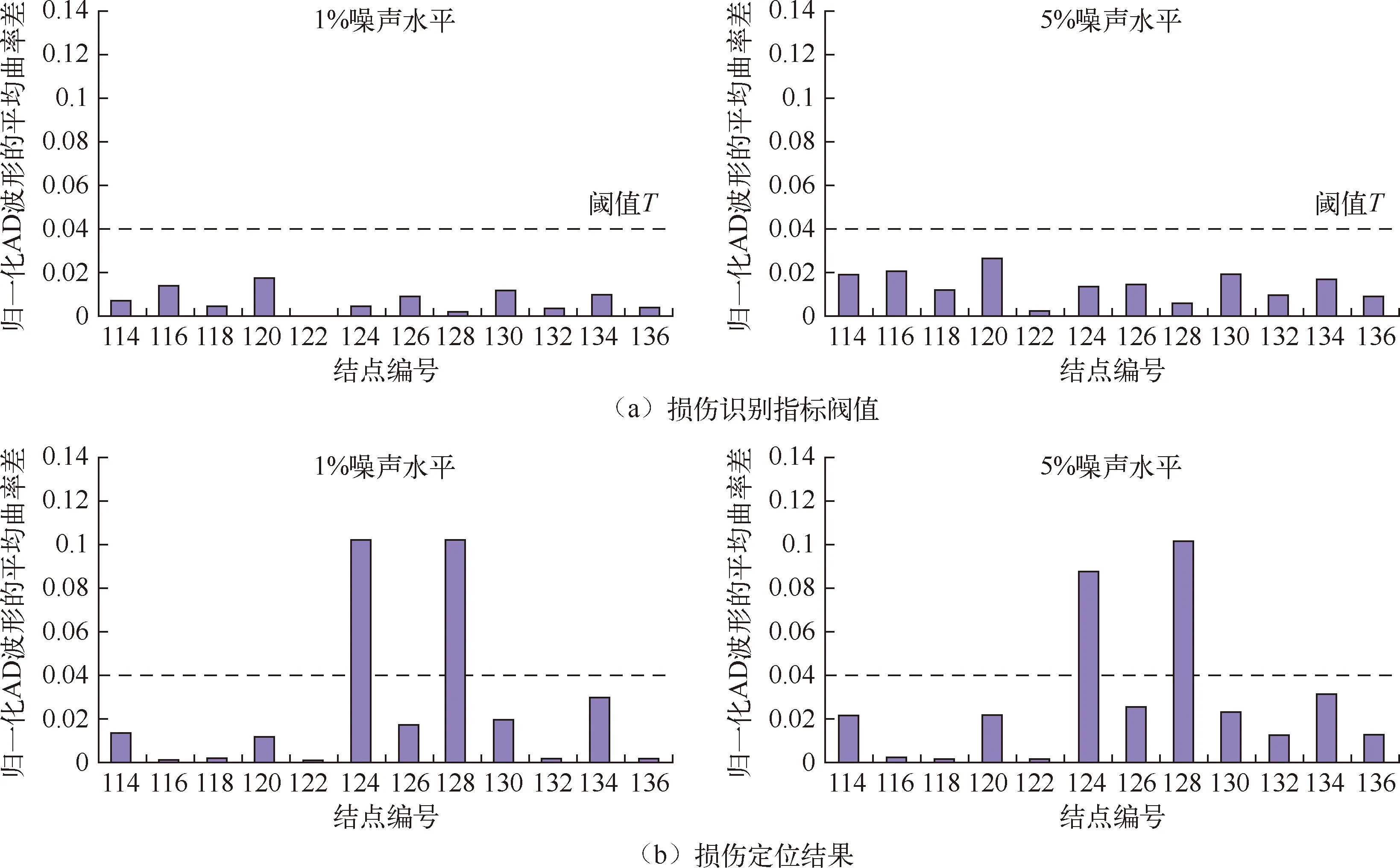
图4 运用“AD 波形法”识别工况1在不同噪声水平下的损伤定位结果

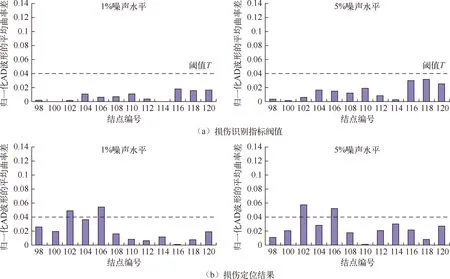
图5 运用“AD 波形法”识别工况2在不同噪声水平下的损伤定位结果

图6 运用“AD 波形法”识别工况3在不同噪声水平下的损伤定位结果

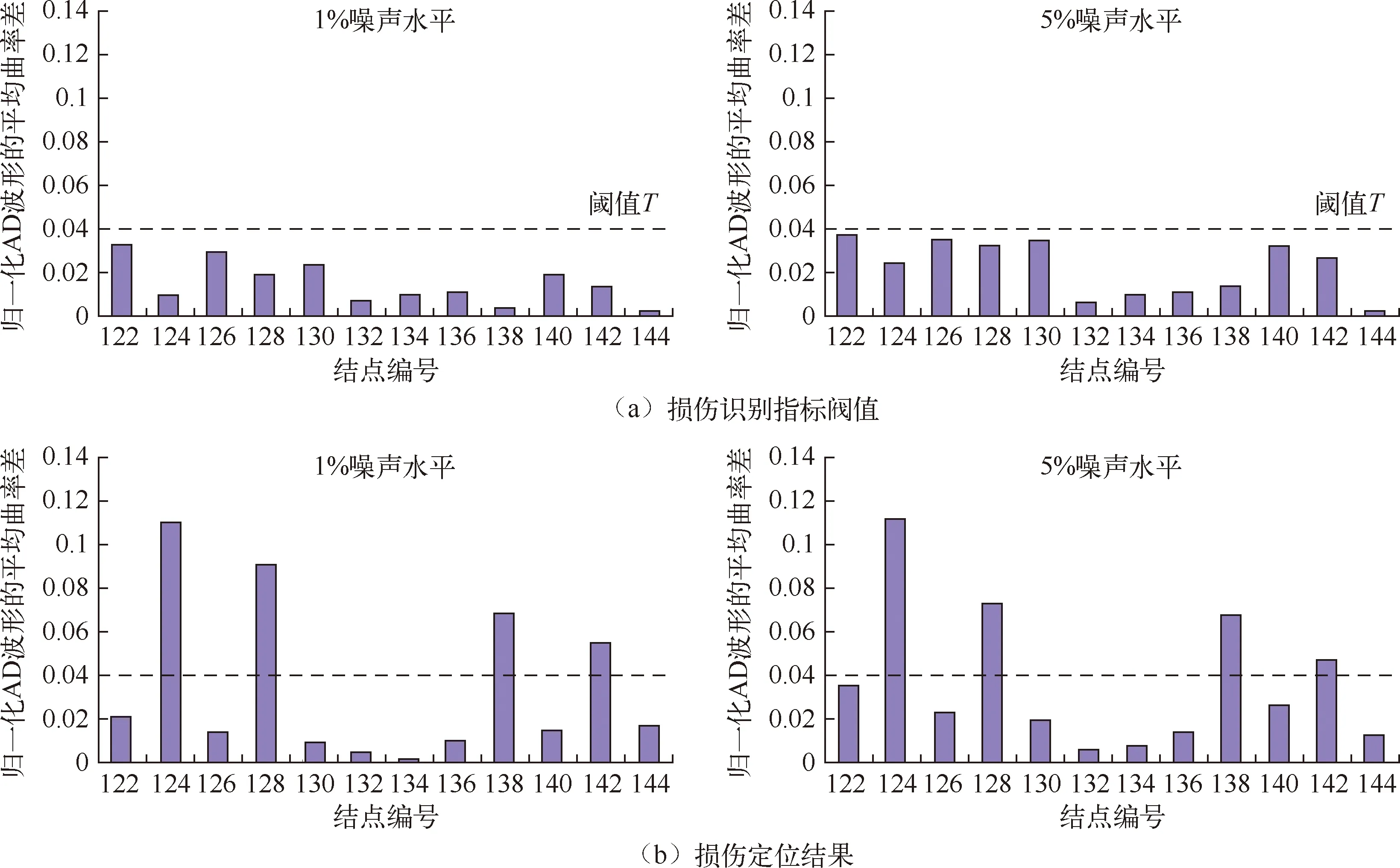
图7 运用“AD 波形法”识别工况4在不同噪声水平下的损伤定位结果

2.3.2 归一化位移方差波形的平均曲率差法(简称“DV 波形法”)

所有工况均采用与损伤单元相近的15个结点数据进行分析，考虑实际测量中频率的噪声水平，分析添加1%噪声水平后的损伤识别情况。损伤定位的阀值计算也由相同的结点集来确定,得出归一化位移方差波形的平均曲率差法测定的损伤定位识别结果。

图8(a)～11(a)分别为各工况主梁各节段完好状态下损伤识别指标阀值，从图中可知，添加1%噪声水平后，平均曲率差阀值统一确定为0.05。图8(b)～11(b)分别为各工况下主梁各节段损伤定位结果，即各测点的损伤判别因子值。由于损伤判别因子值为曲率指标，所以对两个边界点不能进行计算，但对于边单元依然具有识别效果，因此两边界范围内即为损伤点。单损伤工况下，图8中124单元～128单元发生了突变，容易识别出范围内对应的结点126单元为损伤单元；图9中102单元～106单元发生了突变，容易识别出范围内对应的结点104单元为损伤单元。双损伤工况下，图10中104单元～108单元，116单元～120单元均发生了突变，容易识别出范围内对应的结点106单元、118单元为损伤单元；图11中124单元～128单元，138单元～142单元均发生了突变，容易识别出范围内对应的结点126单元、140单元为损伤单元。因此，在任意损伤情况下，归一化位移方差波形的平均曲率差法均能成功定位出了预设的损伤部位。

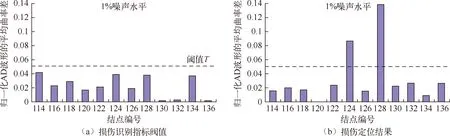
图8 运用“DV 波形法”识别工况1在不同噪声水平下的损伤定位结果

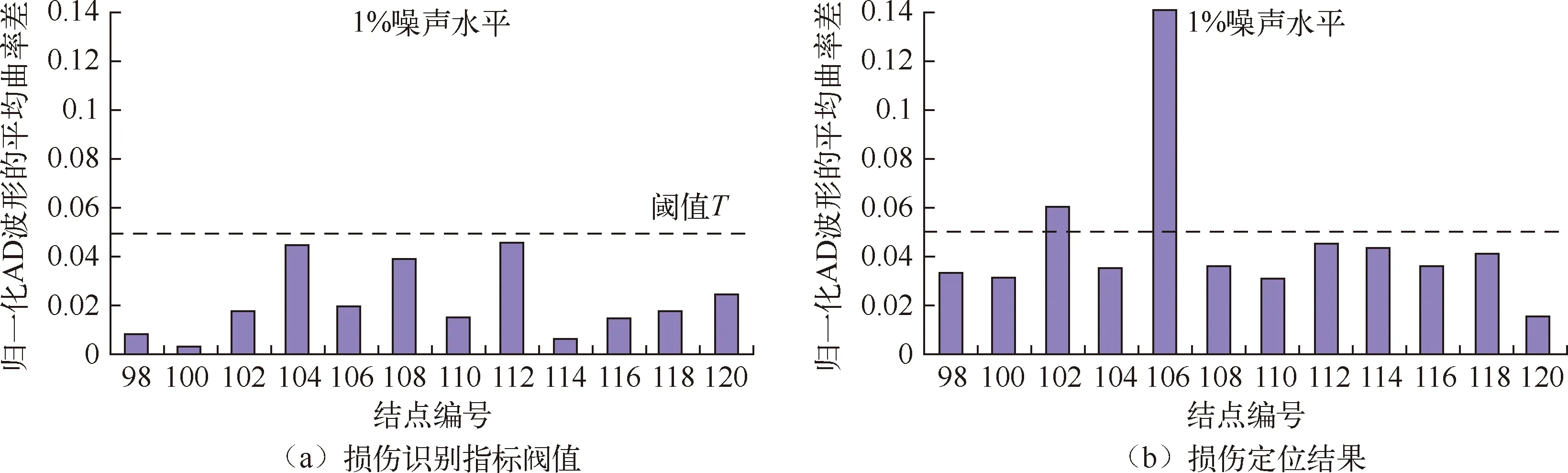
图9 运用“DV 波形法”识别工况2在不同噪声水平下的损伤定位结果

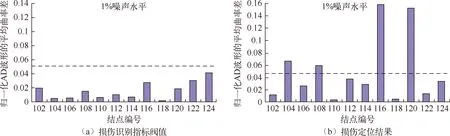
图10 运用“DV 波形法”识别工况3在不同噪声水平下的损伤定位结果

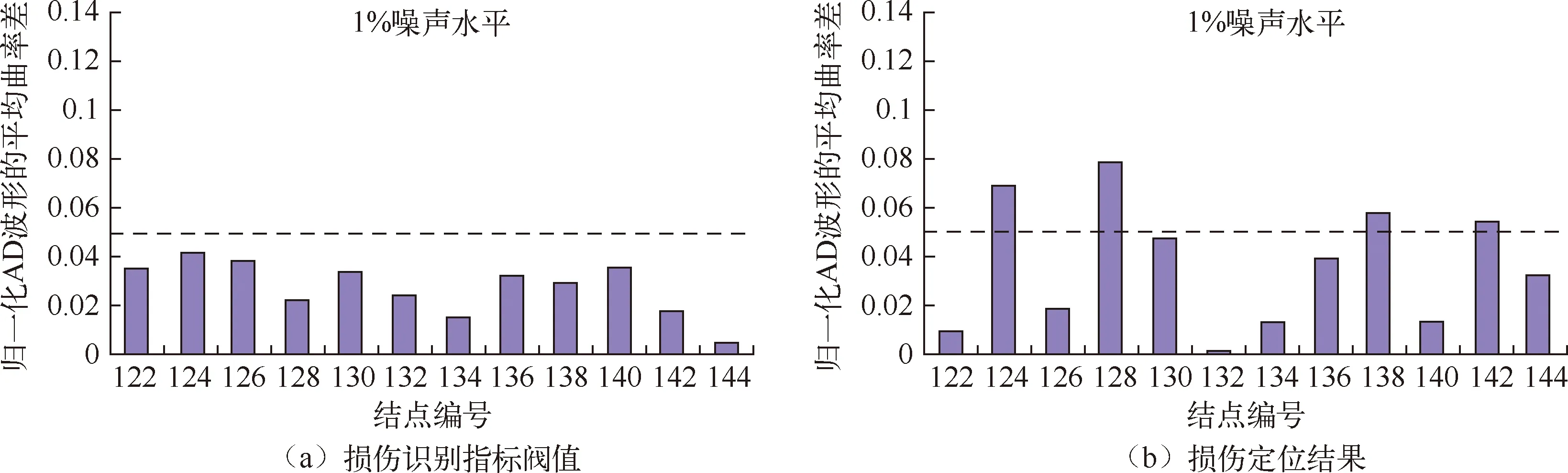
图11 运用“DV 波形法”识别工况4在不同噪声水平下的损伤定位结果

3 结论

(1) 通过试验手段获取数据，结合MATLAB、SAP2000等有限元仿真软件,模态曲率法能较好地运用于桥梁结构损伤识别。

(2) 基于归一化位移均值波形和归一化位移方差波形的平均曲率差法，无论在单损伤还是双损伤下均能准确识别损伤位置，具有较高的鲁棒性、较好的适用性。

(3) 模态平均曲率差法虽能检出损伤但却不能区分损伤类型, 以及通过检测出的损伤进而预测剩余寿命，都需要在下一阶段的研究中加以完善。