基于HCA-Bayes的矿井涌水水源识别

顾爱民，刘德民

(华北科技学院 安全工程学院，北京 东燕郊 065201)

0 引言

矿井水害问题一直是制约我国煤矿安全生产的重要因素，及时准确地识别涌水水源是制定防治水措施、实施涌水救援的关键[1-3]。由于水化学特性是地下水最本质的特征，目前众多学者针对水化学特征研究出多种涌水水源识别方法，其中：张靖苑[4]在水化学数据的基础上通过将主成分分析与随机配置网络相互结合，有效的提高了数据集的可分性，降低了模型中冗余的指标。董东林等[5]在不同含水层水化学特征差异的基础上通过欧氏距离建立矿井混合水的水源识别模型，具有一定的适用性。陈绍杰等[6]在残差分析的基础上引入主成分都思想，并结合水化学特性建立的模型能更加准确的确定矿井水的来源和数量。秋兴国等[7]通过分析水质离子之间的相关性，运用变异系数法确定权重，实现对水源识别模型的改进；施龙青等[8]运用主成分分析法消除叠加信息的影响，并通过引入粒子群算法优化了极限学习机，使得收敛速度显著加快，具有极佳的可靠性。侯恩科等[9]采用逐步回归分析筛选出主要的判别因子，随后通过最小二乘支持向量机对样本进行训练，有效的排除了干扰因素的影响。王甜甜等[10]引入动态权重的思想，综合主观以及客观因素，使得判别指标符合实际需要，提高了水源识别的可靠性。赵伟等[11]依据质心距理论并结合Fisher判别，通过因子分析对样本进行训练，使得误判率大幅度降低。以上的科研工作者通过结合不同的统计学方法使得水源识别模型更加完善，减轻或者消除单一判别模型的缺点。鉴于此，本文利用层次聚类(HCA)具有定量分析样本间亲密程度，实现样本亚类划分的特点，结合贝叶斯判别(Bayes)模型判别速度快，识别质量高的优势，建立了基于HCA-Bayes的矿井涌水水源识别模型，提高了矿井涌水水源的识别精度。

1 理论分析

1.1 层次聚类(HCA)

层次聚类(HCA)原理[12-15]是通过计算两类数据点间的距离，对最为接近的两类数据点进行组合，并反复迭代这一过程，直到所有数据点合成一类，并生成聚类谱系图。

首先计算聚类统计量，聚类统计量是用来反应各水源样本间关系疏密程度的指标，这里选择平方欧式距离作为聚类统计量，用dij表示，由dij确定相似关系矩阵。

(1)

随后分别计算n个样本两两间的距离dij,选择距离最小的两类,合并成一个新类,重新计算合并后的新类与其他各类间的距离,再将距离最小的两类合并,重复以上过程至，最终样本聚为一类。对于类间距离计算方法有很多,本文拟采用瓦尔德法来计算类间距离。

最后将上述分析结果用聚类谱系图表示出来，通过谱系图直观的看出所要研究的水源样本点不断聚成一类的过程，从而依据相应的类间距离对原始数据进行亚类划分。

1.2 贝叶斯判别(Bayes)

贝叶斯判别(Bayes)是建立在贝叶斯准则基础上进行判别分析的-种多元统计分析法，它从样本的多元分布出发，充分利用多元正态分布概率密度提供的信息计算后验概率，然后确定样本归属。

设有k个矿井涌水水源(母体)记为g(g=1，2，…,k)服从正态分布，其p元正态分布密度函数为:

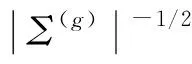
(2)

式中，μ(g)和Σ(g)分别是第g总体的均值向量和协方差阵，令：

(3)

取对数并去掉与g无关的项,记为:

(4)

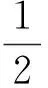
(5)

分别计算y(g/x),g=1,2,…,k。选取其中最大值所对应的类别即为待判水样x所属类别。

2 实例应用

2.1 研究区概况

钱家营井田位于河北省唐山市，隶属开平煤田，位于开平向斜的东南翼。井田含煤地层为石炭系上统和二叠系中统及下统地层，基底为中奥陶统马家沟组石灰岩，可采与局部可采煤层为5、7、8、9、11、12煤层。矿井直接涌水含水层为14煤层顶板至12煤层底板砂岩裂隙含水层、12煤层顶板至5煤层底板含水层、5煤层顶板至A层铝土岩底板砂岩裂隙含水层。

14煤层顶板至12煤层底板砂岩裂隙含水层富水性弱，局部较强。单位涌水量0.0197～0.0566 L/(s·m)，渗透系数0.150～10.707 m/d，该层以中、粗砂岩为主，厚度约30 m，矿井的主要巷道、运输、回风及采区集中上山布置在本含水层，出水形式主要为裂隙水。该含水层涌水以消耗净储量为主，主要为顺层补给。

12煤层顶板至5煤层底板含水层富水性弱。工作面揭露时只出现局部滴、淋水现象，单位涌水量为0.016～0.0584 L/(s·m)，渗透系数为0.154～1.742 m/d，开采工程在此层位每遇到构造均会出现滴淋水现象。

5煤层顶板至A层铝土岩底板砂岩裂隙含水层富水性中等，局部较强。单位涌水量为0.0603～0.228 L/(s·m)，渗透系数为0.095～4.526 m/d。工作面揭露该含水层涌水后沉淀乳白色胶状物质。该含水层含水性不仅与岩性有关，同时也受补给条件和构造断裂控制，整个含水层在井田范围内具有典型的裂隙水特点。

2.2 水样采集及水化学分析

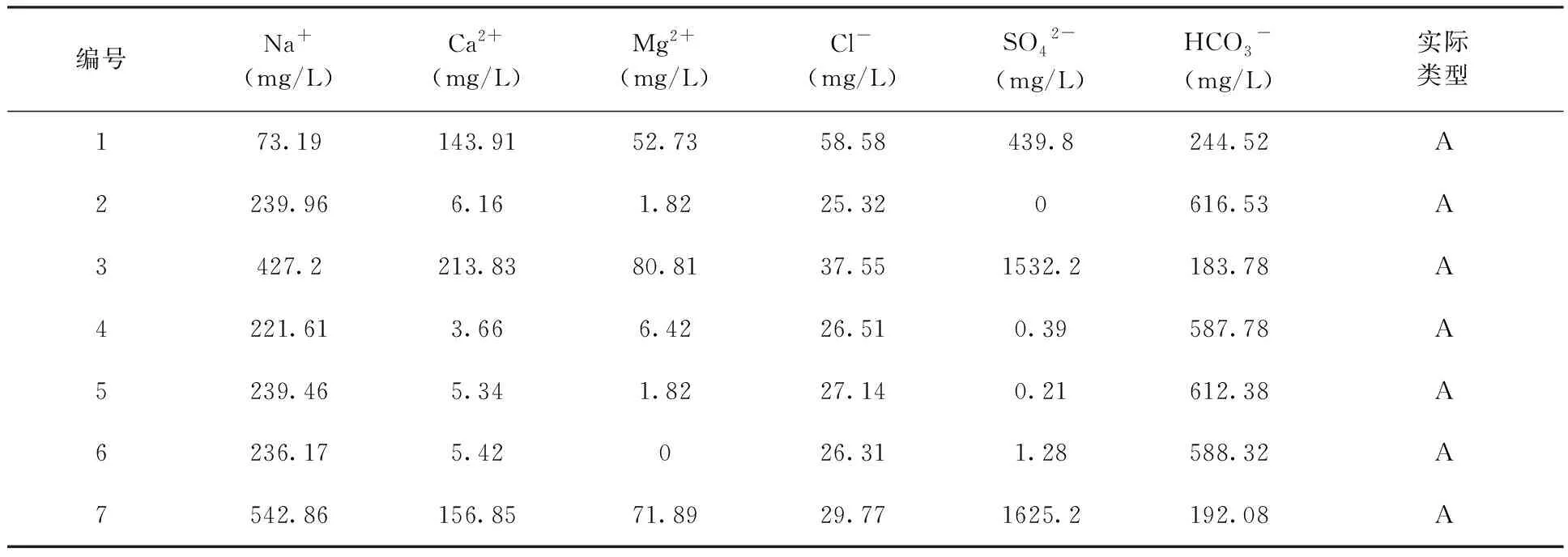
表1 钱家营矿原始水样数据

续表

将表1中33组训练水样经过Piper三线图进行水化学分析，如图1所示。从图1中可以看出14煤层顶板至12煤层底板砂岩裂隙含水层(A类)水样相对集中分布在菱形右上区域，水质类型为S04-Na·Ga和HCO3·SO4-Ca·Na·Mg，12煤层顶板至5煤层底板含水层(B类)水样在菱形图上分布较为分散，水质类型为HCO3-Na、HCO3·SO4-Na·Ca，5煤层顶板至A层铝土岩底板砂岩裂隙含水层(C类)水样主要分布在菱形图下部区域，水质类型为HCO3-Na、HCO3-Na·Ca。可看出同一含水层的水样点呈现出不同的水质类型，主要是因为矿井水化学演化机理复杂，受到地质条件，含水层岩性等多种因素的影响，即使对于同一含水层的水样都会产生很大变化，因此如果对同一含水层的水样点不加以细分就建立水源识别模型，势必会造成误判。本文尝试利用层次聚类分析(HCA)对同一含水层水样进行亚类划分，在划分出的亚类基础上建立水源识别模型。

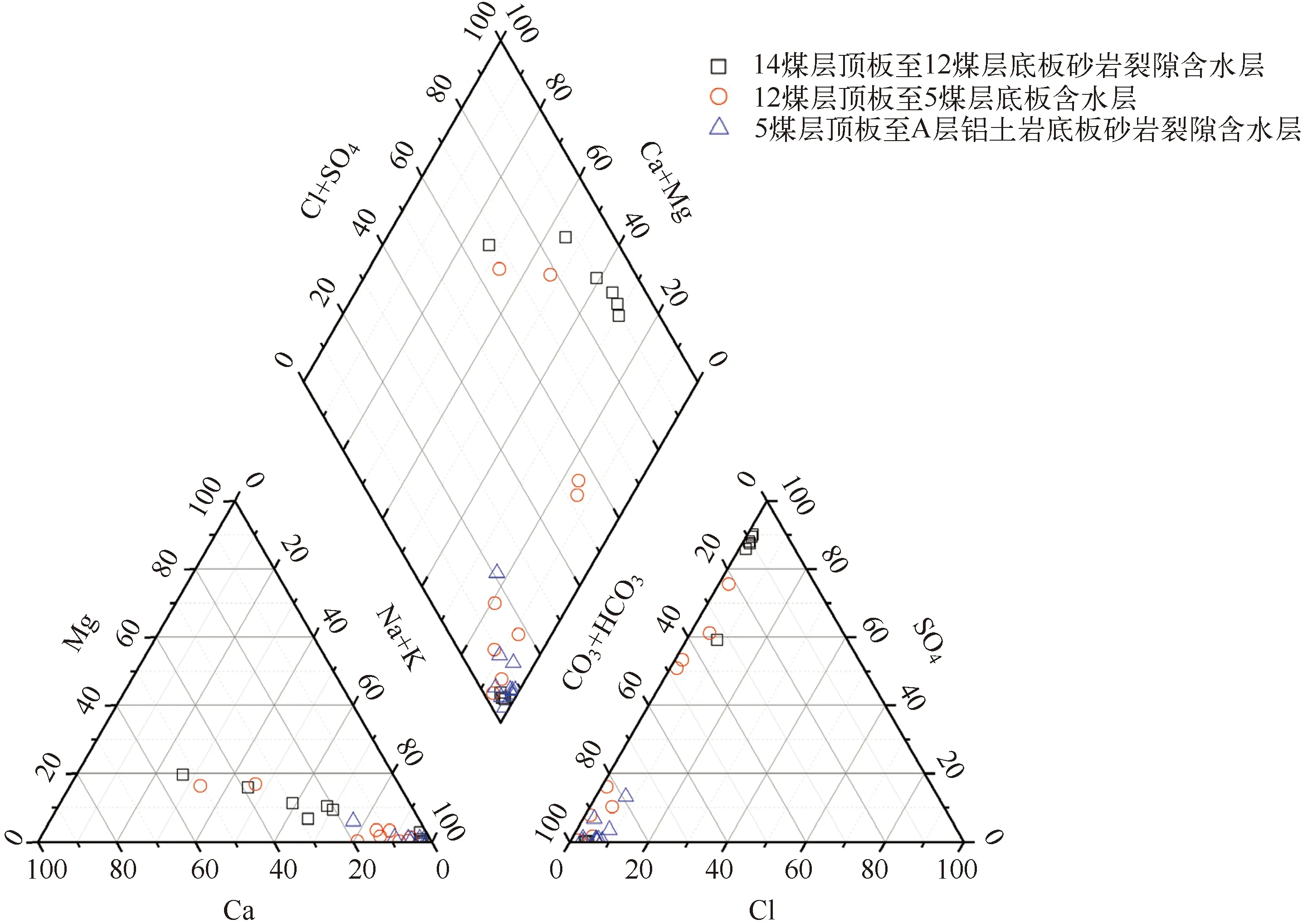
图1 矿井直接涌水含水层Piper图

2.3 矿井涌水水源识别模型

根据Piper图分析的结果，现运用SPSS25.0软件对表1中A、B、C三类含水层水样分别进行层次聚类分析(HCA)，聚类方法选择瓦尔德法，测量区间选择平方欧氏距离。A类水样聚类分析结果如图2所示，根据Piper图上A类水样分布的特点，选取类间距离15作为亚类划分的标准，A类中11类水样被划分成两个亚类，其中编号1、2、4、5、6、9水样归为一类，表明这六个水样水化学特征具有相似性，记为A.1类，编号3、7、8、10、11水样归为一类，记为A.2类，说明A.1类与A.2类水样在水文地球化学特征上存在差异，这与A类水样点在菱形图上的分布一致。同理，B类水样的层次聚类分析结果如图3所示，在类间距离选定为15时，编号12、13、14、15、18、19、20、21归为一类，记为B.1类，编号16、17、22归为一类，记为B.2类。如图4所示C类水样在类间距为15时分成了C.1类和C.2类。C.1类为编号23、24、27、28、29，C.2类为编号25、26、30、31、32、33。

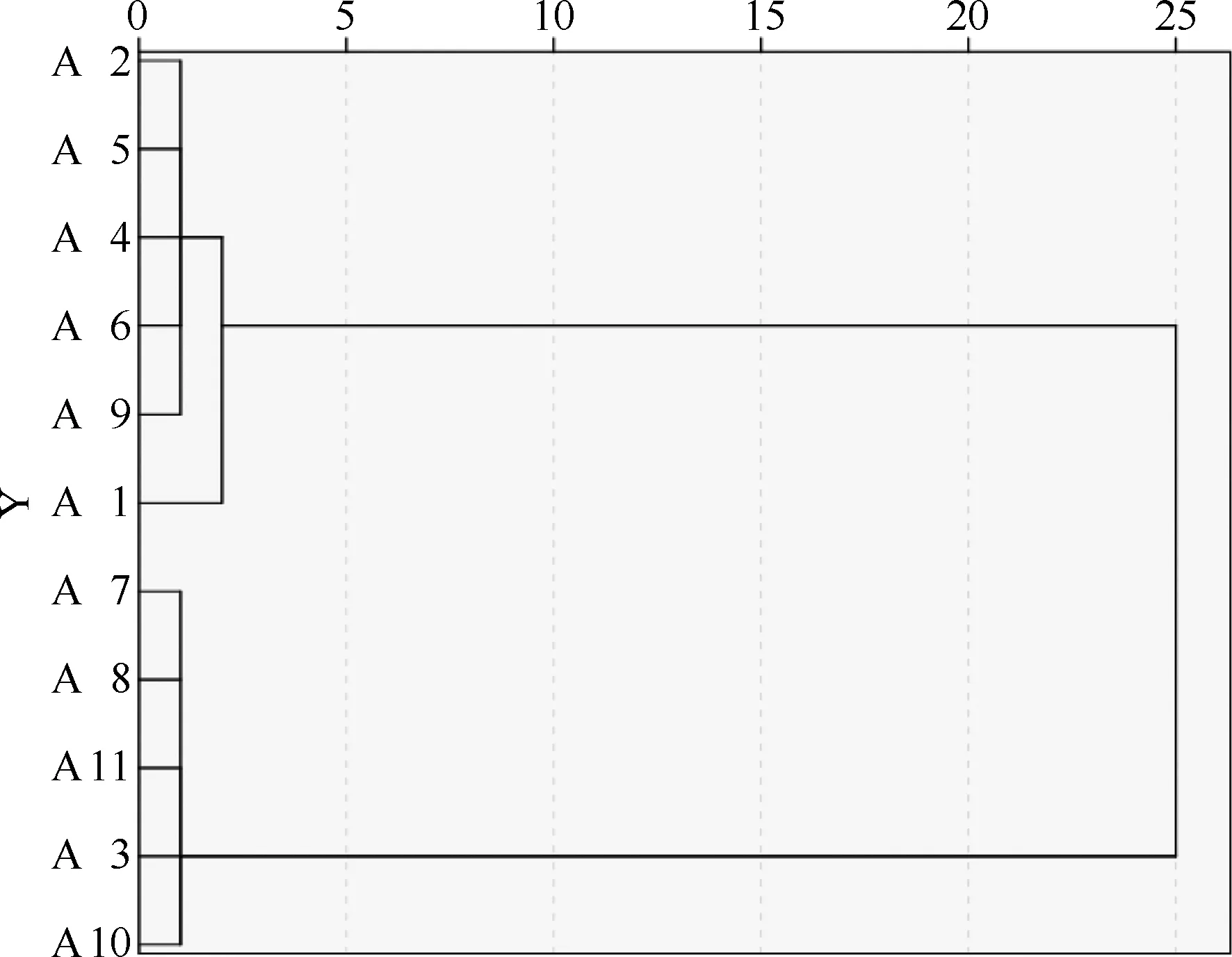
图2 A类水样层次聚类分析谱系图

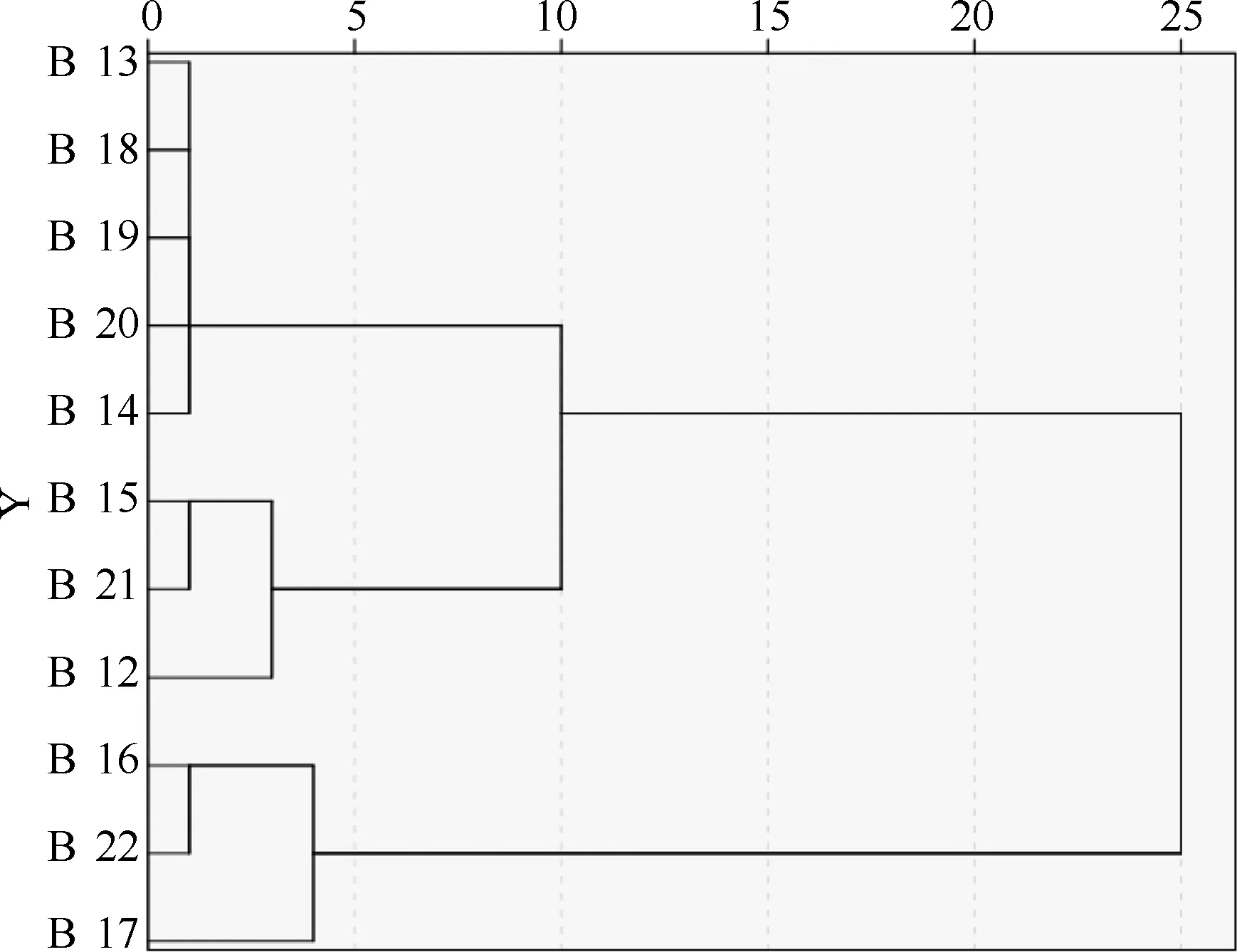
图3 B类水样层次聚类分析谱系图

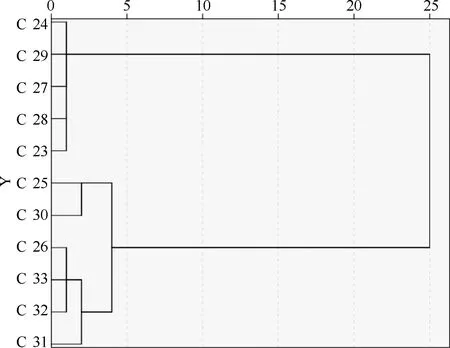
图4 C类水样层次聚类分析谱系图

由此层次聚类分析将33个训练样本的A、B、C三类含水层划分成A.1、A.2、B.1、B.2、C.1、C.2这六个亚类，根据Bayes理论，在训练样本分割成六个亚类基础上建立Bayes判别函数如下：

fA.1=-19.274+0.033x1+0.096x2+0.136x3+0.347x4-0.017x5+0.027x6

fA.2=-97.637+0.539x1+0.520x2+1.282x3-0.554x4-0.135x5-0.149x6

fB.1=-23.755+0.089x1+0.216x2+0.214x3+0.201x4-0.041x5+0.016x6

fB.2=-60.913+0.371x1+0.434x2+0.888x3-0.180x4-0.105x5-0.074x6

fC.1=-22.528+0.192x1+0.234x2+0.426x3+0.386x4-0.092x5-0.037x6

fC.2=-10.303+0.116x1+0.169x2+0.267x3+0.171x4-0.055x5-0.016x6

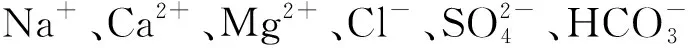
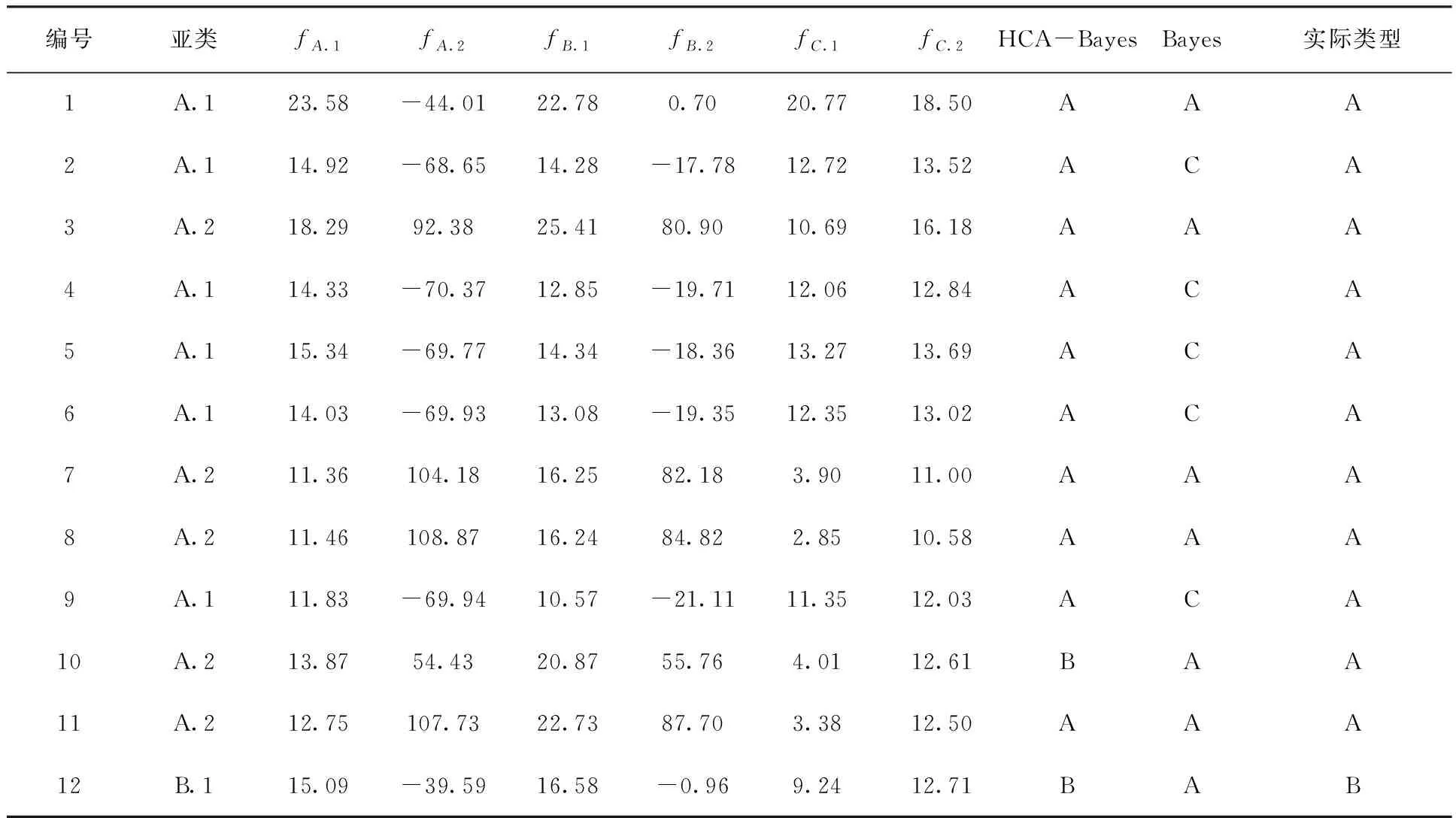
表2 HCA-Bayes模型与Bayes模型回判预测结果

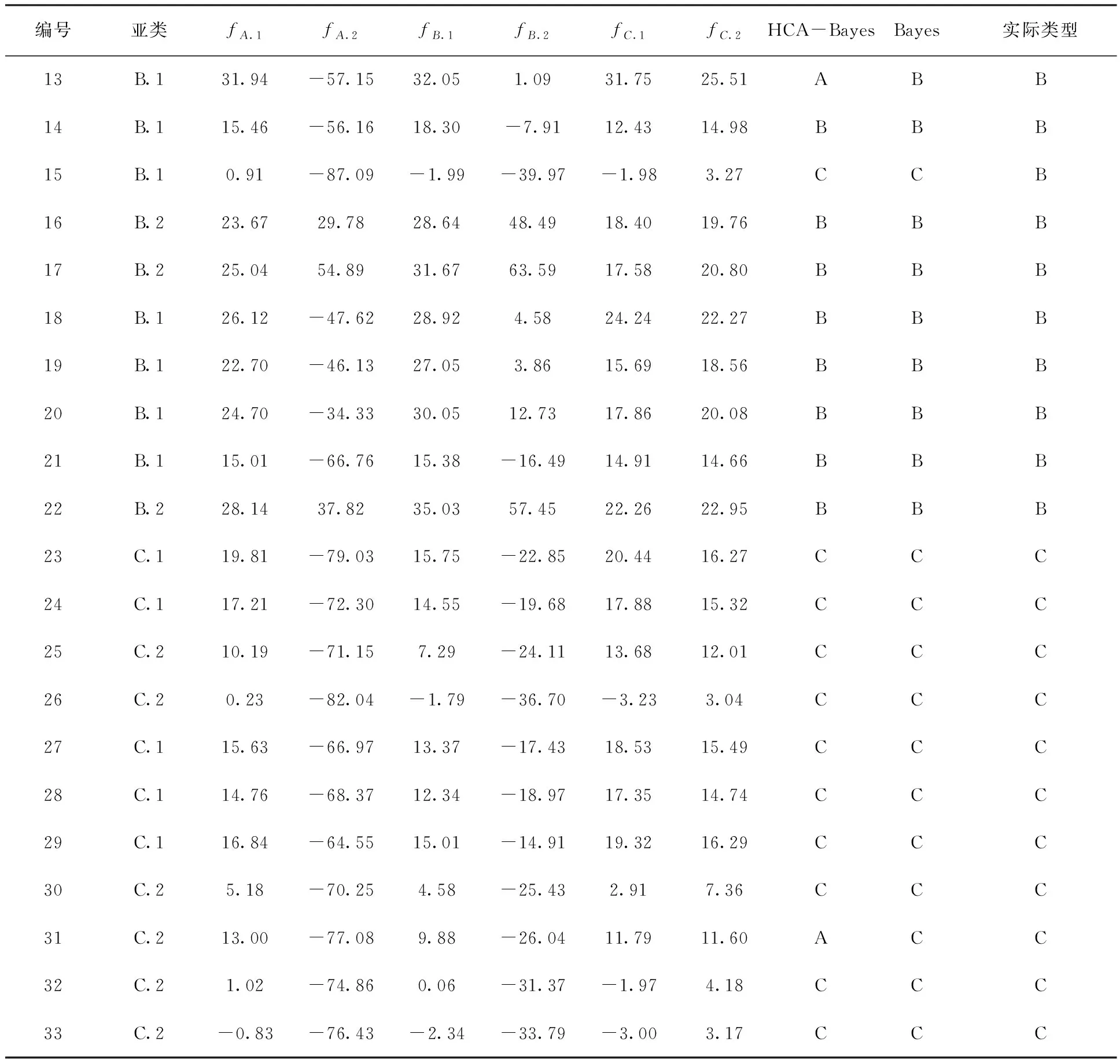
续表

由表2可以看出预测结果基本于真实情况吻合，准确率较高，满足现场精度需要。现通过33组训练样本建立Bayes判别模型并进行回判预测，回判预测结果如表2所示，可直观看出Bayes判别模型误判率为21.2%，HCA-Bayes模型的误判率仅为12.1%，与单纯采用Bayes判别模型相比HCA-Bayes模型的精度较高。

2.4 模型检验

为进一步验证HCA-Bayes模型的识别效果和准确性，对1*～3*号测试样本分别进行Bayes模型与HCA-Bayes模型的预测判别，判别结果如表3所示。 Bayes判别模型在判断2*号样本时误判成A类水样,2*号水水源样本的实际类型为B类(12煤层顶板至5煤层底板含水层)，由图1 Piper图上可知，B类(12煤层顶板至5煤层底板含水层)水样点分布较为分散且一部分水样点与A类(14煤层顶板至12煤层底板砂岩裂隙含水层)水样较为接近，水质信息重叠，因此单纯的建立判别模型很难体现出该模型的特征，从而产生误判。而本文提出的HCA-Bayes模型对3个测试样本预测均与实际情况一致，可以有效的对矿井涌水水源类型进行诠释。

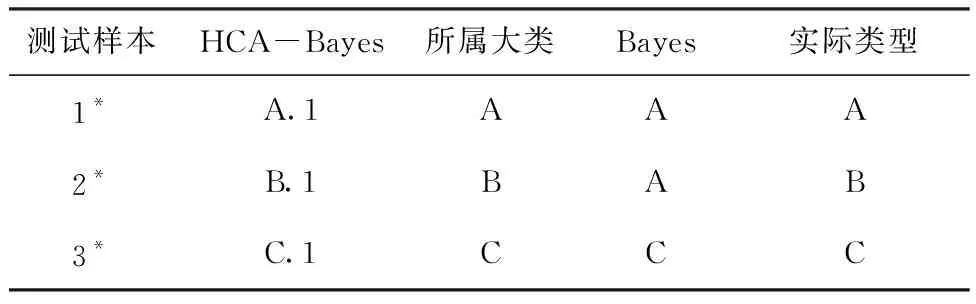
表3 测试样本判别结果

3 结论

(1) 在矿井水文地质条件的基础上，利用Piper三线图分析了三类直接涌水含水层的水化学特征，由于同一含水层水样分布较为分散且各含水层水样数据间存在信息重叠，仅依靠单一的涌水水源识别模型无法准确识别水样。本文利用层次聚类(HCA)对三类含水层进行亚类划分，减少了水样点较为分散的影响，提高了识别精度。

(2) 本文建立的HCA-Bayes模型相比于单一的Bayes识别模型，回代准确率明显提高，对3个测试样本进行预测，预测结果与工程实际情况完全一致，识别质量和可信度较高，可为煤矿防治水工作提供一种新的思路。

(3) 该模型是在钱家营矿的工程基础上建立的，可能受水文地质条件以及数据的影响。因此，在实际应用中还需结合不同煤矿的特点对模型的适用性进行验证，并不断完善。