规则波作用下斜开槽防波堤的波浪力研究

李 尧，李启况，李佳昊，郑子涵，尹则高*

(1.中国海洋大学工程学院，山东 青岛 266100; 2.青岛市城阳区农业农村局，山东 青岛 266109; 3.山东省交通规划设计院集团有限公司，山东 济南 250101)

引 言

防波堤作为一种常见的海岸工程结构物，可以保护港池或者海水浴场等免受外海波浪的侵袭，为船舶正常泊稳作业和居民生产生活提供有力的保障，在海岸防护工程中具有不可替代的作用。斜坡式防波堤是当前世界上使用较为广泛的防波堤之一[1]，对港池内水域有较好的掩护作用，并且其工程技术已经十分成熟，造价相对低廉，施工简便，在各沿海地区得到广泛应用[2]。然而，传统斜坡式防波堤会使掩护水体(例如港池内水域)与外海之间的水体交换受到很大限制，易产生港池内水体污染等问题[3]。开孔防波堤是在传统防波堤的堤身开设孔洞，以提供内外侧水体交换的通道；开孔可以减少防波堤对波浪的反射，降低防波堤所受的波浪力，提高港池内外的水体交换效率，符合绿色发展可持续的基本要求，是一种简单有效的新型海岸防护结构物。近年来，诸多学者通过理论分析、物理试验和数值计算等方法对波浪和海岸结构物的相互作用进行了大量研究。

波浪与斜坡结构相互作用的方面，杨锦凌等[4]利用Fluent软件模拟了规则波在不可渗透斜坡堤上的爬高和越浪，与物理试验结果吻合较好。Lin等[5]在斜坡式海滩上布置了斜坡式海堤模型，研究海啸作用下波浪与海堤的相互作用，定量地分析比较了波浪对海堤的压力、海堤的越浪量和波浪的最大爬高等参数；发现波浪力最大可达静水压力的60%～70%；随着波浪非线性增强，越浪量单调增加；与斜坡上未设置海堤的工况对比，发现设置海堤可以将波浪最大爬高降低20%左右。Lauro等[6]利用试验与数值计算结合的手段分析了一种嵌套有越浪式波能发电装置的防波堤稳定性，结果表明：装置所受最大垂直荷载、水平荷载和整体失效的临界条件并非同时发生，水平荷载最大时垂直荷载为0。Vicinanza[7]对一种基于传统抛石防波堤的越浪式波能转换装置的波浪荷载进行了试验研究，探讨了防波堤附近波面形状和波浪荷载的时空分布。

透水海岸结构的主要优点是水深较大时建造成本较低，并且对海洋环境的干扰较小，所以受到诸多学者的青睐。Jarlan[6]于1961年首次提出开孔墙式防波堤，随后Jarlan型防波堤在实际工程中广泛应用。在此基础上，诸多学者提出了各种新型透水结构。波浪与透水结构相互作用的研究的理论研究方面，Isaacson等[9-10]通过特征函数展开法，研究了垂直开槽防波堤能量耗散特性与防波堤孔隙率和入射波陡等因素的关系，探讨了双层垂直开槽防波堤与波浪的相互作用，结果表明：双层防波堤的透射系数和最大水平力大于单层防波堤对应值。Bergmann等[11]研究了不同波参数和结构孔隙率工况下的透水垂直墙压力分布，并与不透水墙的理论公式进行了对比，引入两个与结构孔隙率相关的参数解释透水墙处的非线性过程，随后建立了新的压力分布预测公式。

本文结合斜坡式防波堤和开孔防波堤的优势，提出了一种安全、高效和环保的斜开槽防波堤，通过在堤身开设三个高度不同的斜槽，以满足不同水深条件下的透水性和安全性需求。

1 物理模型试验

1.1 模型设计

在中国海洋大学水动力实验室的波浪水槽中，开展了相关的物理模型试验。水槽总长度为25 m，宽1 m，高1.2 m。定义波浪的传播方向为x方向，沿水深方向为y方向，造波端底部中点为坐标原点。在模型的迎、背浪侧分别安装3支和2支波高仪，用于采集波浪传播经过斜开槽防波堤前后各个位置的波高数据，波高仪的位置根据Goda[12]于1976年提出的两点法分离入反射波的方法布置，水槽外固定摄像机，用于拍摄波浪与斜开槽防波堤相互作用的过程。试验水槽的首端使用推板造波，末端采用U形结构加消波网消波，斜开槽防波堤在水槽中的具体布置如图1所示。

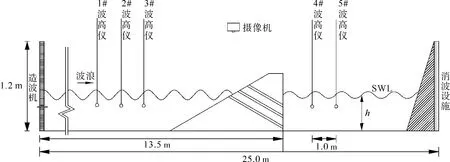
图1 试验布置图

本试验所需的斜开槽防波堤模型采用木板和PVC板制作，防波堤高度d为0.8 m，长度c为1.59 m，宽度a为1.0 m，堤顶宽度b为0.2 m，斜坡坡度θ为30°，槽与竖直面的角度为60°，开槽宽度D为0.03 m；槽由四块PVC板组成。将三个槽由下到上分别命名为底槽、中槽和顶槽，背浪侧槽口的中心高度dL，dM，dU分别为0.05 m，0.20 m，0.35 m。模型示意图如图2所示。

图2 斜开槽防波堤模型示意图

1.2 试验工况

参考我国南海东北区域的某典型海域状况[13]并依据《波浪模型试验规程》[14]，确定本试验斜开槽防波堤物理模型的几何比尺1∶10，时间比尺1∶3.16。按照物理模型试验手册的规定[15]，选取三组静水深h=0.40，0.50，0.60 m，五组入射波周期T=1.6，1.8，2.0，2.2，2.4 s，四组入射波高H=0.06，0.09，0.12，0.15 m，总计60组试验工况，与实际海域中4.0～5.0 m水深、0.6～1.5 m波高和5.1～8.6 s波周期相对应。

1.3 试验现象

波浪传播到达防波堤，与防波堤相互作用，沿斜坡向上爬高(h=0.50 m，T=2.0 s，H=0.09 m工况的波峰作用和波谷作用分别见图3(a)和图3(b))；防波堤迎浪侧出现波浪壅高现象，背浪侧出现水面波动现象。波浪流经迎浪侧槽口时，h=0.50 m，T=2.0 s，H=0.12 m工况的水面降低，并伴有气泡出现(见图3(c))。当波浪爬高较大时，h=0.50 m，T=2.2 s，H=0.12 m工况出现波浪破碎现象(见图3(d))。此外，当静水深、入射波高和入射波周期均较大时，存在明显的堤顶越浪现象(见h=0.50 m，T=2.4 s，H=0.15 m工况的图3(e))。

图3 不同典型工况的试验照片

2 水动力数学模型

本章使用FLOW-3D软件对斜开槽防波堤所受的波浪力进行了数值模拟计算，并利用物理模型试验数据验证了数学模型的可靠性。进而研究了不同静水深、入射波参数和开槽宽度等因素对斜开槽防波堤所受的波浪力的影响，并得出了相应的结论。

2.1 控制方程与紊流模型

假设本文模拟的波浪运动的流体是恒温的不可压缩的粘性流体，则控制方程为连续性方程和动量守恒方程。

连续性方程：

(1)

动量方程：

(2)

(3)

(4)

式中，x，y，z表示方向；u，v，w为x，y，z方向的速度分量；Ax，Ay，Az表示流体的面积分数；VF为流体体积分数；ρ为流体密度；p为压强；Gx，Gy，Gz表示重力加速度；fx，fy，fz表示流体粘滞力加速度。

采用RNGk-ε紊流模型封闭方程组，其紊动动能k方程和紊动耗散率ε方程为：

(5)

(6)

式中，C1，C2和C3一般取1.44，1.92和0.20；DT和Dε为扩散项；PT为紊动动能k的产生项。

2.2 边界条件

数值波浪水槽设置见图1所示，斜开槽防波堤的尺寸与位置、波高仪的位置同物理模型试验一致。斜开槽防波堤的三维水动力数学模型的整体网格边界条件如图4所示。水槽前端采用Wave边界条件；末端为出流边界(Outflow)，在边界前设置海绵层(Sponge Layer)；将水槽左、右边壁设置为对称边界(Symmetry)条件；将水槽的顶部设置压力入口(Specified pressure)边界；水槽底部采用固壁边界(Wall)条件。三维坐标轴上均采用均匀网格，最大网格尺寸为0.01 m，同时采用嵌套加密的方式，防波堤和波面附近区域进行网格加密，加密区网格尺寸为0.005 m，最大网格尺寸比设为2∶1，在保证数值模拟试验准确反应流场情况的同时，又大大提高了工作效率。

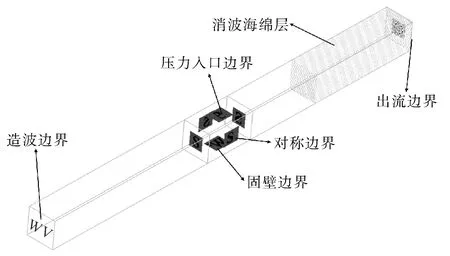
图4 边界条件示意图

2.3 数值模型的验证

图5给出了开槽宽度D=0.03 m，静水深h=0.60 m，入射波高H=0.06 m和入射波周期T=1.8 s工况下，防波堤迎浪侧x=10 m处和背浪侧x=14 m处的数值计算波高与物理试验值的对比。可以看出波形时程曲线变化虽然存在一定程度的偏差，但整体趋势一致，只有个别点稍有浮动，试验值与计算结果误差一般在8%以内，两者吻合较好，说明本文建立的规则波作用下斜开槽防波堤的数学模型是较为合理可靠的，可以进行后续的计算工作。

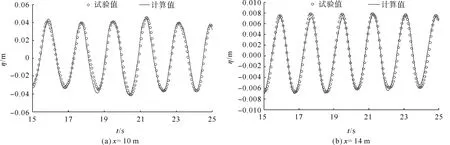
图5 斜开槽防波堤作用下典型测点波面时程曲线(D=0.03 m，h=0.60 m，H=0.06 m，T=1.8 s)

基于验证后的数学模型，对不同开槽宽度、静水深、入射波周期以及不同入射波高下斜开槽防波堤所受的波浪力进行计算，共设置180组数值模拟计算工况见表1。

表1 数值模拟计算工况

3 结果与分析

本章主要利用数值模拟计算结果分析结构受到的波浪力，计算不同波浪参数、静水深和开槽宽度下斜开槽防波堤所受的水平波浪力(FH)和垂直波浪力(FV)。水平波浪力正向与波浪行进方向一致，垂直波浪力正向垂直向下。

3.1 波浪力时程变化

图6给出了开槽宽度D=0.03 m，静水深h=0.50 m，入射波高H=0.09 m，入射波周期T=2.0 s工况下，斜开槽防波堤受到的水平波浪力和垂直波浪力的时程变化曲线。由图可知：斜开槽防波堤受到的波浪力变化曲线近似为正弦曲线，且其周期与入射波周期相同；垂直波浪力较大而水平波浪力较小。

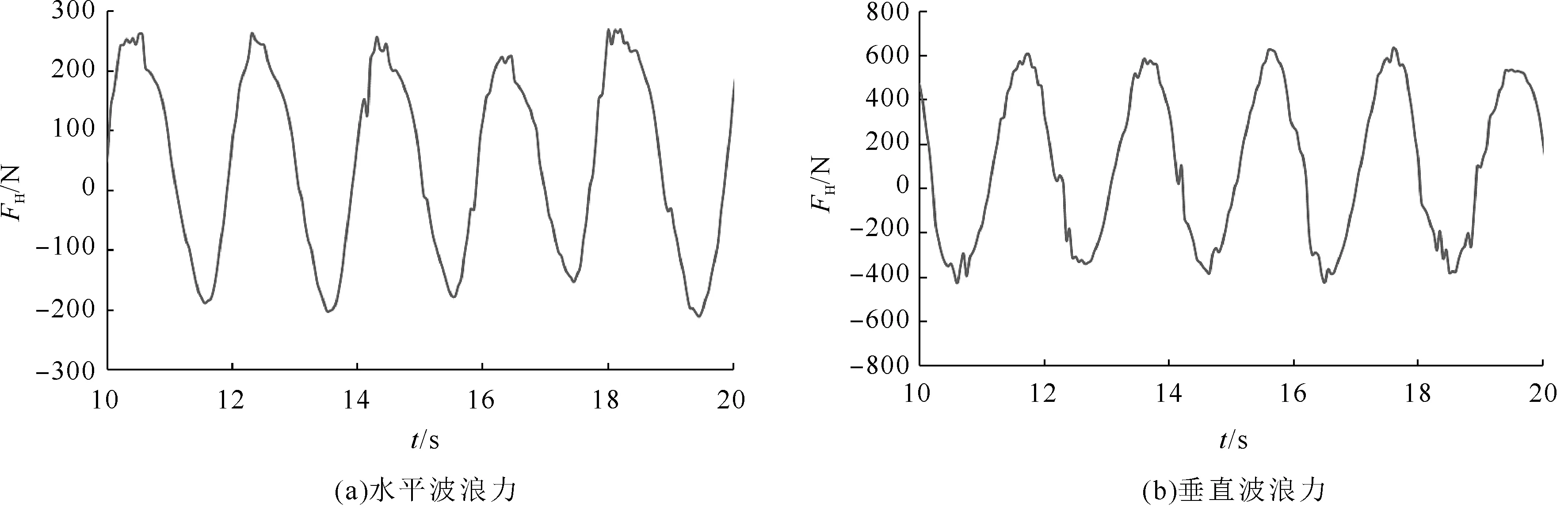
图6 斜开槽防波堤受到的波浪力的时程曲线(D=0.03 m，h=0.50 m，H=0.09 m，T=2.0 s)

3.2 最大水平波浪力

为研究方便，定义8个波周期内斜开槽防波堤受到的水平波浪力峰值的平均值为最大水平波浪力(FHmax)，垂直波浪力峰值的平均值为最大垂直波浪力(FVmax)。

图7(a)给出了开槽宽度D=0.03 m，静水深h=0.50 m工况下，斜开槽防波堤受到的最大水平波浪力FHmax与入射波高H的关系。由图可知：随着入射波高增加，斜开槽防波堤受到的最大水平波浪力均呈递增趋势；不同入射波周期条件下增加趋势近似相同。图7(b)给出了开槽宽度D=0.03 m，入射波高H=0.09 m工况下，斜开槽防波堤受到的最大水平波浪力FHmax与入射波周期T的关系。由图可知：相同静水深条件下，随着入射波周期增加，斜开槽防波堤受到的最大水平波浪力呈递增趋势，h=0.40 m和h=0.50 m工况FHmax增幅大于h=0.60 m工况的对应值；相同入射波周期条件下，随着静水深增加，最大水平波浪力增加。图7(c)给出了静水深h=0.50 m，入射波周期T=1.8 s工况下，防波堤受到的最大水平波浪力FHmax与开槽宽度D的关系。由图可知：不同入射波高条件下，随着开槽宽度增加，防波堤受到的最大水平波浪力呈递减趋势；原因可能是开槽宽度增加使更多的水体通过防波堤的斜槽进入了后方水域，波浪与防波堤的作用面积减小，最大水平波浪力随之减小。

引入无量纲最大水平波浪力，定义为：

(7)

图8 无量纲最大水平波浪力与入射波陡的关系(D=0.03 m)

3.3 最大垂直波浪力

图9(a)给出了开槽宽度D=0.03 m，静水深h=0.50 m工况下，斜开槽防波堤受到的最大垂直波浪力FVmax与入射波高H的关系。由图可知：随着入射波高增加，斜开槽防波堤受到的最大垂直波浪力均呈递增趋势。图9(b)给出了开槽宽度D=0.03 m，入射波高H=0.09 m工况下，斜开槽防波堤受到的最大垂直波浪力FVmax与入射波周期T的关系。由图可知：相同静水深条件下，随着入射波周期增加，斜开槽防波堤受到的最大垂直波浪力呈递增趋势；相同入射波周期条件下，随着静水深增加，最大垂直波浪力增加。图9(c)给出了静水深h=0.50 m，入射波周期T=1.8 s工况下，防波堤受到的最大垂直波浪力FVmax与开槽宽度D的关系。由图可知：相同开槽条件下，随着入射波高增加防波堤受到的最大垂直波浪力均呈递增趋势；相同入射波高条件下，随着开槽宽度增加，防波堤受到的最大垂直波浪力均呈递减趋势，原因可能是开槽宽度增加导致波浪与防波堤的作用面积减小，作用强度减弱，因此最大垂直波浪力减小。

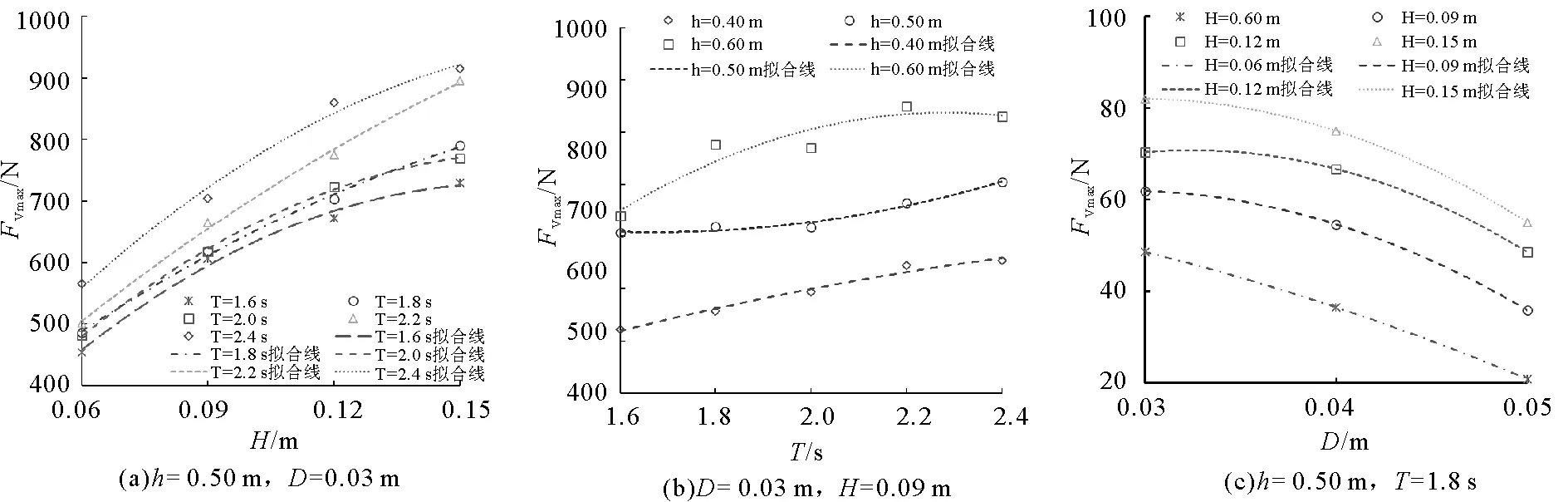
图9 波参数与开槽宽度对最大垂直波浪力的影响

引入无量纲最大垂直波浪力，定义为：

(8)

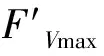
图10 防波堤受到的无量纲最大垂直波浪力与入射波陡的关系(D=0.03 m)

4 结论

本文利用室内物理模型试验和数值模拟计算相结合的方法，对规则波作用下斜开槽防波堤所受波浪力进行了研究。结论如下：(1)规则波作用下斜开槽防波堤的波浪力研究的数值模拟计算结果与试验结果较吻合，说明建立的数学模型是较合理可靠的。(2)斜开槽防波堤受到的水平波浪力和垂直波浪力均随时间周期性变化，受到的垂直波浪力明显大于水平波浪力。(3)随着静水深、入射波高和入射波周期的分别增加，防波堤受到的最大水平波浪力和垂直波浪力均相应增加；相同周期条件下，随着入射波陡增加，无量纲最大水平波浪力和垂直波浪力均相应增加，且入射波周期越大，其增幅越大。(4)随着开槽宽度增加，最大水平波浪力和垂直波浪力均减小，说明在实际工程中保证防波堤结构稳定和消波效果的前提下可适当提高开槽宽度，减少其所受的波浪力。