基于EMD-SVM的钛合金铣削过程刀具磨损监测*

2022-11-04谢振龙岳彩旭刘献礼严复钢刘智博穆殿方梁越昇

振动、测试与诊断 2022年5期

关键词：频域特征值刀具

谢振龙，岳彩旭，刘献礼，严复钢，刘智博，穆殿方，梁越昇

（1.哈尔滨理工大学先进制造智能化技术教育部重点实验室哈尔滨，150080）

（2.佐治亚理工学院乔治·W·伍德拉夫机械工程学院亚特兰大，30332）

引言

智能制造是包括原材料、加工及测量检测等一系列环节的生产过程，刀具是其中非常关键的环节［1］。刀具磨损作为最主要的刀具失效形式，关乎着制造的精度及产品的表面质量，如何精确识别刀具磨损已成为一个研究热点。

近些年，专家们提出了许多刀具磨损识别的方法，主要分为直接观察法和间接观察法。直接观察法就是测量刀具磨损量来衡量刀具磨损程度，包括监测磨损宽度、磨损面大小等。常用的方法有接触法、辐射法和光学检测法。它存在2个主要缺陷：①不能对刀具磨损状态进行实时监测；②停机检测极大降低工作效率。间接观察法就是通过检测刀具铣削时产生的信号，构建基于信号的刀具磨损模型，从而监测刀具磨损的方法。此方法不对加工过程造成干扰，且可以连续监测加工过程，更适合于在线监测。常用的方法有切削力监测［2］、声发射监测［3］、振动监测［4］、电流与功率监测［5］、超声波监测［6］和温度监测［7］。然而单纯采集铣削时的信号不能准确反应刀具状态，机器学习及信号处理技术为刀具磨损识别提供了新的思路。Rizal等［8］提出了一种结合多传感器信号和马氏田口系统的检测刀具磨损的方法，并提出马氏距离作为识别刀具磨损的评价指标。Bhuiyan等［9］对切削时的声发射及振动信号进行研究，探究刀具磨损与信号之间的关系。Wu等［10］通过多信号融合探究刀具剩余寿命，揭示信号与刀具磨损之间的关系。Chen等［11］通过深度置信网络学习模型融合刀具力信号、振动信号及声发射信号对刀具磨损进行识别。谢峰云等［12］提出的广义BP神经网络识别模型，提取了振动信号广义均方根、广义功率谱密度均方根及小波包系数均方根为特征值，将特征值输入BP神经网络中识别铝合金铣削时的颤振。甘梓舜等［13］通过对机床的各种信号进行监测从而监测刀具磨损。陈刚等［14］通过BP神经网络对振动及切削力信号进行学习从而识别刀具磨损。但是由于深度学习及其他学习模型所需数据量大、运算速度慢，BP神经网络准确性相对不稳定，而SVM由于其算法简单以及具有优秀的“学习”能力［15］，所以笔者采用SVM对数据进行学习，从而达到刀具磨损识别的效果。

利用信号对刀具磨损状态识别会面临一个问题，即采取的信号往往掺杂着噪声，所以对信号进行处理至关重要。Plaza等［16］通过对比不同的信号处理方法，选择小波包与神经网络结合的方式对信号进行处理监测表面质量，但是由于小波包基有选择困难的局限，选用小波包基会花费较长的时间且监测的信号会出现非线性、非平稳的现象。为了解决这个问题，Huang等［17］提出了经验模态分解，该方法对于分析信号非线性与非平稳具有明显的优越性，同时克服了小波包基选择困难的特点。在处理信号时选择EMD将会简化数据的计算且不会失去数据原有的特性，因此将EMD引用到信号监测中对信号进行处理。

由于采取的信号数据量大，直接输入信号进行学习及判断会增加模型运算时间，所以应当提取信号特征值来对数据进行简化。刀具磨损时，加工过程中的时、频域和能量分布将发生变化。为了有效地监测信号的变化，选取的特征值应当囊括以上特征。标准差可以反映信号能量的变化，它的值随信号幅度的增大而增大。功率谱熵［18］是一个无量纲指标，其可以反映不同频率在频带内的分布。当频率分量广泛分布在频带上时，分布的不确定度最大，其所对应的功率谱熵最大；相反，当频率分量分布在一定频带上时，频率分布的不确定性最小，其所对应的功率谱熵最小。I-kazTM是一种多分辨率分析方法，能准确得出信号的变化［19］。因此，将标准差、功率谱熵和I-kazTM作为信号的特征值。

基于以上分析，笔者针对钛合金切削过程中的刀具磨损识别问题，提出了一种基于EMD及SVM刀具磨损阶段识别方法。首先，将原始加速度信号及力信号分解为一系列IMF，选择有用的IMF来组合一个新的信号；其次，计算新信号的特征值，将得到的特征值矩阵作为SVM的输入；最后，得到了刀具磨损识别模型，能对刀具磨损阶段进行准确识别。

1 信号处理及特征值的选取

1.1 EMD分解思想

EMD方法假设任何信号都由不同IMF组成，每个IMF可以是线性的，也可以是非线性的。IMF分量必须满足2个条件：①其极值点个数和过零点数相同或最多相差1个；②其上下包络关于时间轴局部对称。

EMD分解过程基于以下假设：

1）信号最少有2个极值，即1个极大值和1个极小值；

2）时域特性由极值间隔决定；

3）如果数据序列完全缺乏极值但仅包含拐点，那么它也可以通过1次或多次求导来表示极值点，而最终结果可以由这些成分求积分来获得。

具体方法是由一个“筛选”过程完成。

首先，找出信号s（t）所有的极大值点并将其用3次样条函数拟合成原数据序列上的包络线，再找出所有的极小值点并将其用3次样条函数拟合成原数据［20］。

其次，计算上下包络线的均值，记为m1（t），并将原数据序列s（t）减去该均值即可得到1个去掉低频的新数据序列h1

因为h1（t）一般不是1个IMF分量序列，为此需要对它重复进行上述处理过程k次，直到h1（t）符合IMF的定义要求：所得到的均值趋于零。这样就得到了第1个IMF分量c1（t），它代表信号s（t）中最高频率的分量

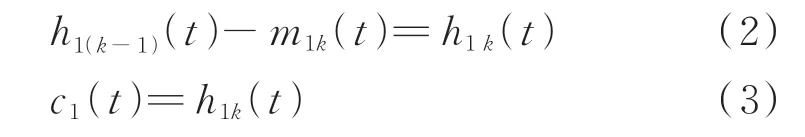
然后，将c1（t）从s（t）中分离出来，即得到1个去掉高频分量的差值信号r1（t）。将r1（t）作为原始数据，重复以上步骤，得到第2个IMF分量c2（t），重复n次，得到n个IMF分量［21］

最后，当cn（t）或rn（t）满足给定的终止条件（通常rn（t）成为一个单调函数）时，循环结束。由式（3）和式（4）得到

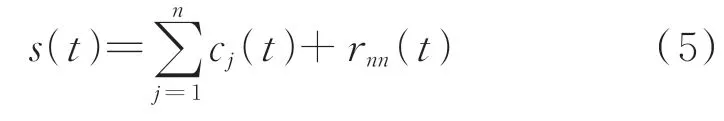
1.2 信号特征值的选取

1.2.1 I-kazTM

I-kazTM是由I-kaz指数演化出来的，其主要思想是将动态信号分解为3个频率范围，其中：低频（LF）范围为0～0.25fmax；高频（HF）范围为0.25fmax～0.5fmax；极高频（VF）范围为大于0.5fmax。为了测量数据分布的散射，计算了每个频带的方差σ2

由于I-kazTM方法是基于数据质心的数据发散概念发展起来的，所以I-kazTM的系数可以用Z∞来表示

将式（6）～（8）代入式（9），得到

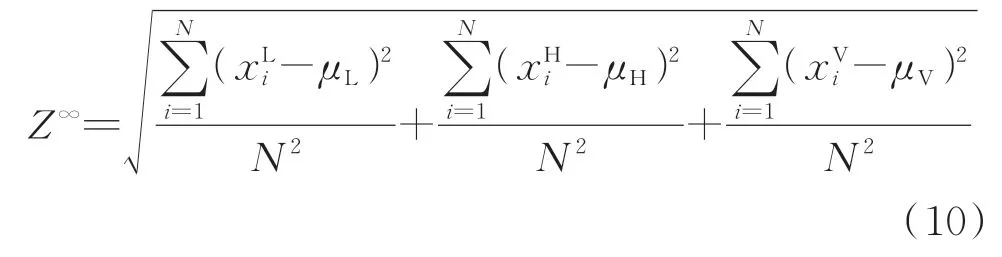
式（10）可以用峰度和标准差表示出来，峰度K的公式为

其中：N为数据的数量；s为标准偏差。

因此，根据峰度K和标准偏差s可得

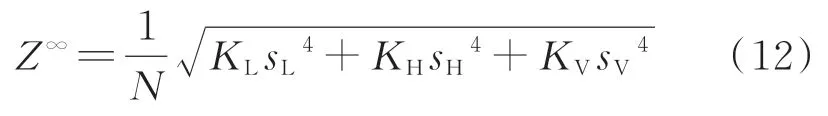
其中：KL，KH和KV分别为LF，HF和VF范围中的信号的峰度；sL，sH，sV分别为LF，HF和VF范围内的信号的标准差。

根据I-kazTM来提取适应EMD分解的方法，其不同于I-kazTM，即信号不需要分解为三差分。EMD处理完信号后，选择有效的模态分量，分别计算其峰度及标准偏差，最终计算I-kazTM系数。因此，I-kazTM系数可以写成如下形式

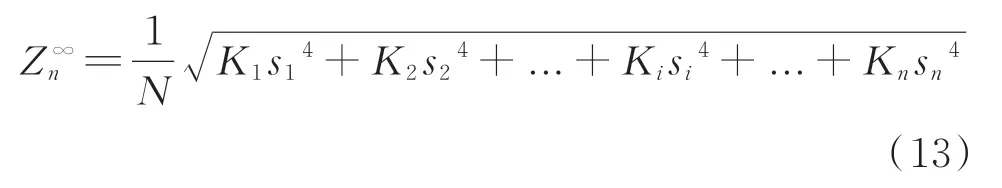
其中：N为有效分解模态的数目；Ki为分解后模态的峰度；si为第i个分解信号的标准偏差。

1.2.2 功率谱熵

功率谱熵（power spectral entropy，简称PSE）是“信息熵”在频域中的扩展，其与频率分量的分布有关。具体计算步骤如下。

1）根据式（14）获得信号x（t）的功率谱

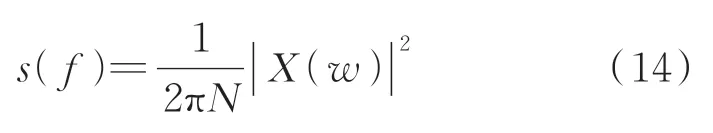
其中：N为数据长度；X（w）为X（t）的傅里叶变换。

2）功率谱的概率密度函数可以通过对所有频率分量的归一化来计算

其中：s（fi）为频率分量fi的光谱能量；pi为相应的概率密度；N为快速傅里叶变换中频率分量的总数。

3）相应的功率谱熵定义为

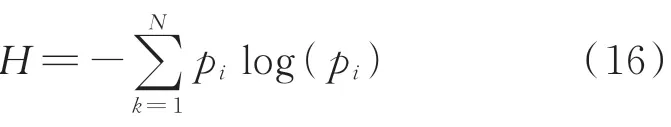
为了比较不同的工作条件，结果由因子logN标准化，得

功率谱熵E是在［0，1］的范围内的无量纲指示符，其中1表示频率分量分布不确定度最大，0表示分布不确定度最小。

1.2.3 标准差

标准差（standard deviation，简称SD）能很客观准确地反映一组数据的离散程度，其计算公式为

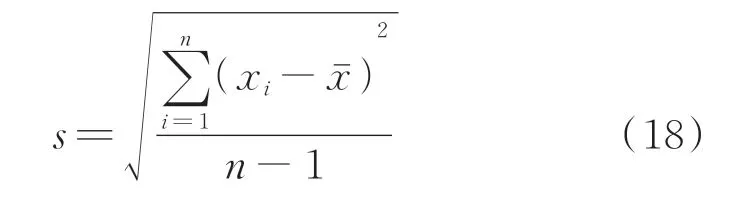
2 基于EMD-SVM刀具磨损识别模式

SVM是一种二分类模型，其基本模型是定义在特征空间上的间隔最大的线性分类器［22］。SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面，其将空间的点进行划分并根据划分的直线对点进行识别，如图1所示。对于线性可分的数据来说，这样的超平面有无穷多个（即感知机），但是几何间隔最大的分离超平面却是唯一的。由于信号特征值相对于信号整体来说，数据量小，易于学习，所以采用SVM对信号进行学习。

图1 支持向量机Fig.1 Support vector machine

在选择核函数时，若对给出的数据没有先验知识，径向基函数（radial basis function，简称RBF）就是最好的选择，而且RBF核的支持向量机可以获得非常平滑的估计［23］，所以笔者采用高斯核函数作为SVM的核函数。

为了消除噪声和其他无关的信号，首先，利用EMD将加速度信号分解为多个IMF，将分解完的信号重构为新信号；其次，将新信号划分成一系列段，分别计算每个分段的I-kazTM、功率谱熵及均方根，得到铣削状态的特征向量矩阵；最后，以特征向量矩阵为输入特征，建立以SVM为基础的刀具磨损识别模型。根据该模型可以判断刀具磨损阶段。刀具磨损阶段识别的流程如图2所示。

图2 基于EMD-SVM的刀具磨损阶段识别流程Fig.2 Process of tool wear stage based on EMD-SVM

3 钛合金铣削实验及信号分析

3.1 实验设备

实验在三轴机床VDL-1000E进行，实验工件材料为Ti-6Al-4V（TC4），实验刀具为无涂层硬质合金四齿铣刀，刀具螺旋角、前角、后角分别为75°，8°和9°。采用PCB加速度传感器及Kister9171A旋转式测力仪对加速度信号及铣削力信号进行采集。采用东华DHDAS动态信号采集分析系统对加速度信号及力信号进行处理，采样频率为1 kHz。图3所示为铣削加工实验现场，旋转测力仪安装在刀柄处对加工实验的3向力信号进行测量，将加速度传感器连接在工件上对加速度信号进行测量，选取有效的信号点作为2种信号的共同起始点。

图3 铣削加工实验现场Fig.3 The milling experiment site

3.2 实验方案及数据分析

3.2.1 实验方案

为了验证该方法，实验准备获取在不同刀具磨损情况下的力及加速度信号，实验参数如表1所示。

表1 实验参数Tab.1 Experimental parameters

如果要对刀具磨损阶段进行划分，就要先确定刀具磨损曲线。在本研究实验参数下进行实验，取3次走刀的平均磨损值作为1次磨损取值，建立如图4所示的刀具磨损曲线。表2为刀具磨损状态分类表，根据磨损率变化情况将刀具磨损过程分为3个阶段，即初期磨损阶段［0 mm，0.12 mm）、正常磨损阶段［0.12 mm，0.17 mm）和急剧磨损阶段［0.17 mm，0.30 mm）。预先将3个磨损阶段标记为1，2，3以输入SVM中。

图4 刀具磨损过程Fig.4 Tool wear process

表2 刀具磨损状态分类表Tab.2 Classification of tool wear status

3.2.2 特征值提取及数据分析

在实验中很难根据原始的加速度及力信号来判断铣削状态。特征提取的目的是为了减少原始加工信号的尺寸，同时保持所提取的特征中具有刀具状态的相关信息。本节主要以加速度信号为例进行数据分析。

选取1组铣削时检测的初期振动信号，经过频域变换处理后的加速度信号及频域分布见图5。

图5 加速度信号及其频域Fig.5 Acceleration signal and its frequency domain

图5所示的加速度信号经EMD分解得到的时域和频域如图6所示。图6（a）中，从左到右依次为IMF1，IMF2，···，IMF6。从图6（b）可以看出，第4～6个模态固有函数的频域极其相近且主频过小，此时的模态固有函数为虚假分量，没有实际意义，可以忽略不计，所以计算时值采取IMF1～IMF3。图中为无纲量单位。

图6 EMD分解时域及频域图Fig.6 EMD decomposition time domain and frequency domain diagram

图7为3个刀具磨损阶段的力信号，刀具磨损量分别为0.05，0.15及0.25 mm。由图可知，当后刀面磨损处于正常磨损时切向力及径向力分别为270和160 N，而当后刀面磨损处于急剧磨损阶段时，2种力信号的幅值急剧增加，比例分别为41%及27%，这是因为刀具后刀面磨损后，作用在后面的法向力及摩擦力都增大，故切向力及径向力增加，而轴向力却未有较大的变化。

图7 不同阶段力变化图Fig.7 Force variations at different stages

图8为刀具在初期磨损、中期磨损及急剧磨损的特征值随时间的变化图，其中特征值为无量纲单位。由图可以看出，在不同的刀具磨损情况下，刀具磨损的特征值趋于一个稳定值，且3个阶段的特征值不同，由此可以得出选取的特征值对信号变化敏感，可以用于模型的学习。

图8 不同阶段加速度信号及其特征值变化图Fig.8 Acceleration signal and its eigenvalue change in different stages

通过对初期、中期及急剧磨损阶段的加速度信号进行对比发现：急剧磨损阶段的加速度信号相较于初期及中期磨损阶段来说，均方根及功率谱熵指数增大而I-kazTM减小，即刀具磨损时信号能量增加，信号的分散性变高。

为了验证上述结论的有效性，重建加速度信号的形态特征、时域能量和频率分量，对信号进行了深入分析。图9为在不同刀具磨损情况下加速度信号的形态特征及频域分布图，其中频域分布图中的频率分量是由刀齿通过频率（270 Hz）和谐波组成。对比不同刀具磨损情况下的频域分布发现：随着刀具磨损的增加，信号的频域由低频向高频部分转移，高次谐波增加，这是因为切削力随刀具磨损的增加而增加进而引起信号的变化；信号呈现周期性波动，这是刀具切入切出的接触特性发生了变化引起的。

图9 不同刀具磨损情况下的加速度信号及其频域Fig.9 Acceleration signal and frequency domain under different tool wear conditions

监测的特征值信号以加速度信号特征值为主，建立加速度信号与力信号特征值特征矩［I-L，E-L，s-L，I-Z，E-Z，s-Z］作为线性分类器的输入，其中：I，E，s分别为I-kazTM、功率谱熵和标准差；L，Z分别为力信号和加速度信号。图10所示为加速度信号构成的特征值空间，由于PSE为接近0的数，为了可以直观地看出特征值在空间的分布，采用1-PSE作为z轴，图中为无量纲单位。由图可见，不同刀具磨损情况下的特征值相互独立且相同刀具磨损阶段下的特征值集中在一起。

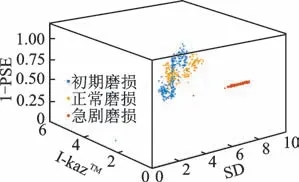
图10 特征值空间Fig.10 The feature space

将每个刀具磨损阶段的160组数据作为训练集，将其余40组数据作为测试集。最后，得到1个大小为160的训练集和1个大小为40的测试集的数据集对EMD-SVM模式进行训练及测试。

为进一步验证建立模型的准确度及运算速度，使用同1组数据作为输入，建立SVM，BP神经网络、EMD-SVM及小波包-SVM这4种模型进行对比。

对于SVM模型及BP神经网络模型，将实验所获取的信号直接输入学习模型中进行训练，然后将测试信号输入到学习好的模型中进行判断。对于小波包-SVM，先将信号进行小波处理后输入SVM构建刀具磨损模型，然后将检测信号输入模型中进行判别。通过对4种模型进行训练后得到了4种模型的混淆矩阵，其准确率对比如图11所示。其中：混淆矩阵纵坐标为预期判断的刀具磨损阶段；横坐标为实际判断出的刀具磨损阶段；两者相交的黑色对角线为预测正确的测试数据。表3为4种模型输入训练信号进行训练及输入检测信号进行识别的运算时间及精度。

图11 4种模型准确率对比图Fig.11 The confusion matrix of three models

表3 不同模型运算时间表Tab.3 Operating time of different models

由于BP网络预测精度不稳定，SVM的泛化能力不稳定，容易出现过拟合，小波包分解由于挑选小波包基困难和其对非平稳及非线性数据上的劣势，训练时间较长；而EMD-SVM由于对信号进行预处理，提取的特征值能更好地表达样本特征，不容易出现过拟合现象且计算效率相对于其他模型高，所以模型准确度较高，泛化能力强，学习所用时间较其他机器学习模型短。对比后发现EMD-SVM的精度最高，运算速度最快。相对于BP神经网络，同1组数据的运算时间节省60%，精度提高了15.12%，对刀具磨损状态有很高的灵敏性，能监测刀具磨损的发生。