基于EWT-FastICA的斜拉桥监测挠度温度效应分离*
2022-11-04谭冬梅姚欢吴浩甘沁霖
谭冬梅,姚欢,吴浩,甘沁霖
(1.武汉理工大学土木工程与建筑学院 武汉,430070)
(2.华中师范大学城市与环境科学学院 武汉,430079)
引言
随着桥梁结构健康监测系统的发展,桥梁的健康状态及安全评估越来越方便高效,但大量的数据积累造成很多有用的信息被掩盖。挠度作为桥梁安全评估最直观的参数之一,其中包括车载作用以及温度作用引起的挠度,混凝土收缩徐变等引起的长期挠度[1]。将这些不同的效应准确分离出来有利于对桥梁进行损伤识别及健康监测,目前有许多学者针对这方面做过一系列的研究。
刘纲等[2]从不同时间尺度展开,以日温差效应频率为中心频率,利用粒子群优化算法自适应的调整滤波器的带宽从而达到分离日温差效应。孙雅琼等[3-4]通过应变监测数据,运用时变的平均值法剔除出温度效应。陈国良等[5]根据挠度响应在时间尺度上不耦合的特点,运用中心移动平均法从时间序列分析来剔除年温差效应和日温差效应,并用差分整合移动平均自回归模型(autoregressive integrated moving average model,简称ARIMA)预测了挠度变形的长期趋势。刘夏平等[6]将温度输入最小二乘支持向量机中得到挠度温度效应来定量分析温度与温度效应之间的关系,根据关系式来从温度变化得到挠度温度效应的变化。梁宗保等[7]建立了应变与温度之间的经验回归方程,将温度效应视作回归方程得到的值与应变测量值之间的差值。谭冬梅等[8]通过采用改进的集合经验模态分解(modified ensemble empirical mode decomposition,简称MEEMD)算法进行多次分解最终对温度效应进行了分离。
笔者提出一种基于EWT-FastICA挠度成分分离算法。首先,采用经验小波变化根据极大值选取原则,在频谱上将日温差效应分割并构造Meyer小波滤波器快速准确分离日温差效应;其次,针对年温差和长期挠度频率相近难分离或者分离效果差的问题,修改傅里叶频谱分割边界,将年温差和长期挠度成分充分分解,形成一系列IMF分量;然后,采用PCA降维,提取主元;最后,运用FastICA算法解混分离出年温差和长期挠度。EWT对比传统的经验模 态 分 解(empirical mode decomposition,简 称EMD)和集合经验模态分解(ensemble empirical mode decomposition,简称EEMD)算法,可以极大地提升运算速度,受噪声影响小,自适应性好,且结合FastICA算法解决了一般算法较难分离年温差和长期挠度的问题。
1 理论简介
1.1 经验小波变换
经验小波变换[9]是一种新颖的时频分析变换方法,它是对传统的小波变换以及EMD[10]的改进。EWT实质是通过自适应分割频谱,提取出原始信号 的 调 幅(amplitude modulation,简称AM)-调频(frequency modulation,简称FM)成分,从而成功地分解出各IMF[11-12]。
EWT首先把信号的傅里叶谱归一化得到频率ωn∈(0,π),再在归一化后的区间上自适应划分将之分割成N份连续的小区间Λn,每个小区间长度为ωn-ωn-1,可以表示为
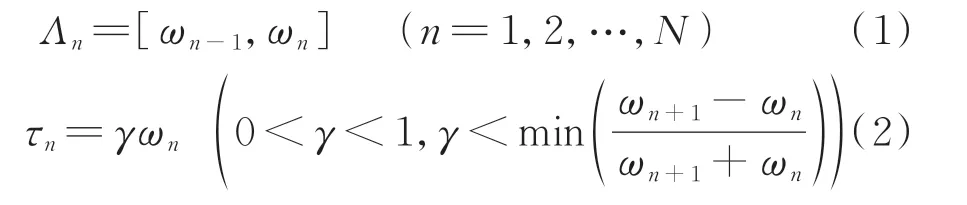
其中:ω0=0,ωN=π。
以每个分割界限ωn为中心设置一个宽度为2τn的过渡带,τn如式2所示,自适应分割后在各区间Λn构造窄带滤波器。根据传统小波变换的定义,经验小波变换的细节系数和近似系数可以表示为
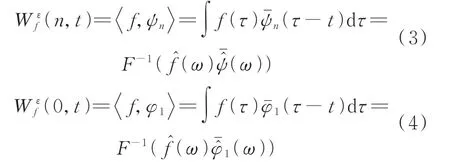
因此,得到的各阶IMF则可以表示为
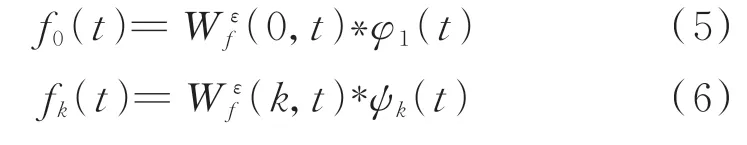
1.2 主成分分析
主成分分析法(PCA)常运用于数据降维,在不损失主要信息的情况下精简了数据,极大提升了计算速度,同时可提取信号中的主元,降低信号中无用成分的干扰以及消除噪声等。通过运用n维向量代替m维向量,其中n<m,PCA的处理步骤可以分为:
1)数据中心化;
2)计算信号的协方差矩阵C=E(XXT);
3)特征值分解协方差矩阵;
4)将分解后的特征值λi按降序排列,选取占比较大的前几个特征值;
5)根据步骤4所求特征值得到其对应的特征向量ω1,ω2,…,ωn;
6)将选取的特征向量构成新的矩阵乘上原信号矩阵实现降维。
1.3 快速独立分量分析
快速独立分量分析(FastICA)[13]是利用快速寻优迭代的方法把采集到的盲信号进行批量分解,找出统计独立的源信号。盲信号指的是混合矩阵以及原始信号均无法知道的情况下,仅仅利用采集到的信号来估计源信号。
设有m个源信号Sn×m=[s1(t),s2(t),…,sm(t)]存在某个混合矩阵An×n,使得

其中:X为观测信号。
在任一时刻t,X均符合式(7)。因此,关键目标则是找出分离矩阵W,其中W=A-1使得Y(t)=为S(t)的估计。
快速独立分量分析可以分为如下步骤:
1)将观测信号X去均值;
2)进行白化预处理;
3)引入定点迭代方式。
定点迭代方式为

其中:E{}为特征值分解;v为白化处理后的数据;g(y)为非线性二次函数的3种形式;a1为常数,通常取为1。
通过近似牛顿法选择系数α,对式(8)两边各自加上αw;根据Kuhn-Tucker条件,在约束条件下,E{G(wTv)}在E{vg(wTv)}+βw=0点取得最优。令K=E{vg(wTv)}+βw,其中β为常数。

此时式(10)变成了可逆的对角矩阵,于是得到如下牛顿近似迭代

两边同乘上E{g′(wTv)+β},最终得到
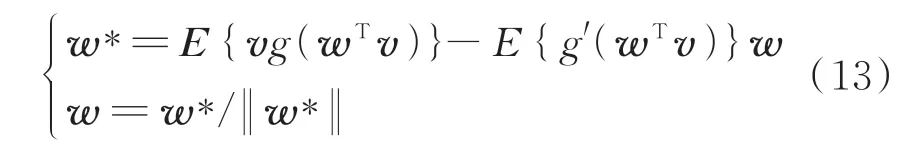
FastICA虽然能很好地解决频率混叠的问题,但是也有着幅值不确定性的缺点。当混合矩阵w某行乘上某个常数k,对应位置源信号同时乘上常数1/k,结果将会不变。
1.4 EWT-FastICA分离流程
首先,利用EWT将桥梁挠度信号分解成为一系列IMF,其中由于日温差效应相比年温差效应以及长期挠度频率有明显的差异,便可根据频率有效地剔除出其中的日温差效应;其次,把剔除日温差效应后剩余的IMF运用PCA降维,根据特征值贡献占比来选取其对应的特征向量,将选取的特征向量与原始矩阵重构得到降维后矩阵;最后,把PCA降维后的矩阵运用FastICA盲源分离算法分解出长期挠度与年温差效应。分离流程如图1所示。
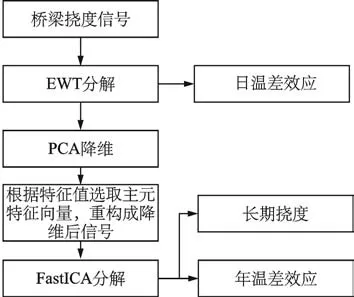
图1 分离流程图Fig.1 Separation flow chart
2 桥梁仿真挠度信号分离
2.1 桥梁模型仿真信号
桥梁挠度作为多种因素共同作用的结果,其长期监测的数据中包括车载和风载等引起的动挠度、温度作用挠度以及混凝土收缩徐变等引起的长期挠度[14],其中温度作用引起的挠度主要包括日温差效应和年温差效应。运用Midas civil软件建立了如图2所示的仿真模型,该模型为武汉某斜拉桥的简要模型。

图2 武汉某斜拉桥的模型图Fig.2 Model drawing of a cable-stayed bridge in Wuhan
根据改变模型温度来观测主跨跨中的挠度变化,其中每升高温度1℃,跨中下挠1.53 mm;每降低温度1℃,跨中上挠1.53 mm。再对跨中截面升高1℃,跨中下挠0.34 mm;截面降低1℃,跨中上挠0.34 mm。根据武汉天气,假设每天平均日温差为12℃,梁横截面日温差可假设为6℃,武汉1年的年温差可以假设为36℃。日温度变化以及年温度变化均可以用正弦函数来表示,由于温度与温度效应之间简化为简单的线性关系[15],所以温度效应亦可表示成正弦函数。
整体日温差效应f11=-9.18sin(πt/12),截面日温差效应f12=-1.02sin(πt/12),因此日温差效应f1(t)=f11(t)+f12(t),年温差效应f2(t)=-27.54sin(πt/4 380)。长期挠度f3(t)根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018),运用指数型函数拟合得到,则总温度效应以及长期挠度可表示为

年温差1个周期为8 760 h。为了方便显示日温差曲线图,日温差只取前4 kh的数据,年温差曲线图取2个周期17 520 h的数据。各个效应时域曲线及频域图如图3~5所示。
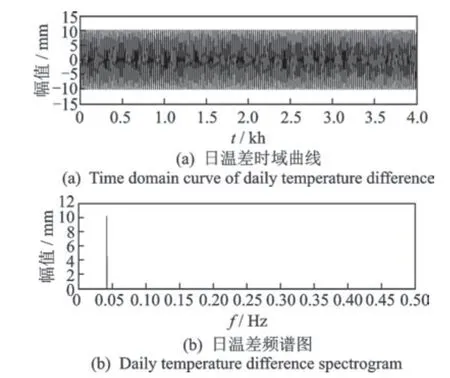
图3 日温差效应时域曲线及频谱图Fig.3 Time domain curve and frequency spectrogram of daily temperature difference effect

图4 年温差效应时域曲线及频谱图Fig.4 Time domain curve and frequency spectrogram of annual temperature difference effect
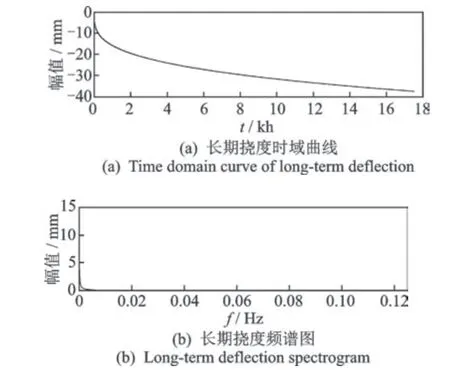
图5 长期挠度时域曲线及频谱图Fig.5 Time domain curve and frequency spectrogram of long-term deflection
2.2 温度效应分离
各效应合成的总挠度时程曲线如图6所示。由于年温差效应的频率为1/8 760 Hz及长期挠度频率过低接近于0,因此一般的分离方法较难分离出年温差效应和长期挠度。
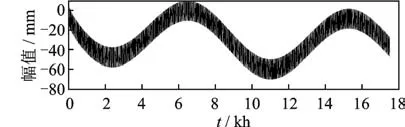
图6 总挠度时域曲线Fig.6 Time domain curve of total deflection
采用EWT对合成挠度信号进行分离,首先,选用Locmax分割策略,在频谱上自动判断选出极大值;其次,在两相邻极大值中间分割,对每个极大值建立Meyer小波滤波器。当取N值为3时,由于0和π总是第1个和最后1个边界,此时在信号频谱上根据极大值还会再次产生2个分割边界。EWT频谱切割图和分割后接近0处的局部放大图分别如图7和图8所示,表明日温差频率部分得到较好的切割,但年温差与长期挠度频率接近,切割效果差。图9为分解后的IMF图,表明对日温差进行了有效的分离(为显示方便,仅显示前4 kh),但长期挠度与年温差存在混叠。

图7 EWT频谱切割图Fig.7 EWT segmentation of spectrogram

图8 EWT分割后接近0处的局部放大图Fig.8 Enlarged local image near 0 after EWT segmentation

图9 EWT分解后IMF图Fig.9 IMF diagram after EWT decomposition
即使选用Locmaxmin分割策略,分割界限位于年温差和长期挠度交汇处,分离得到的年温差与长期挠度也严重混叠。因此,笔者提出在日温差分割界限与年温差长期挠度界限间设定多个分割界限,将年温差和长期挠度混叠部分分离为多个IMF,取自定分割区间数为7,分解如图10所示。
图10中IMF7便是分离出来的日温差效应,由IMF1~IMF6可看出长期挠度与年温差混叠。从原始信号f(t)中剔除掉IMF7,得到长期挠度与年温差效应的混合信号S1(t),将前6阶IMF以及S1(t)组成多通道的混合信号,再运用PCA算法降维提取主元。PCA数据特征值处理结果如表1所示,其中占比为该特征值与所有特征值之和的比值。由表1可知,前2阶特征值远大于其余特征值,占比较大,于是选取该2阶特征值所对应的特征向量来确定降维后的数据,再把降维后的数据运用FastICA算法盲源分离,然后对分离后的结果与原始信号进行幅值对比,把比值作为系数乘上分离后的结果,最终分离出日温差、年温差和长期挠度,各分离结果如图11所示。

图10 EWT分解图Fig.10 EWT decomposition diagram

表1 PCA处理后特征值数据Tab.1 Eigenvalue data after PCA processing

图11 最终分解图Fig.11 Final decomposition diagram
通过相关系数(r)来评价分解效果,其中相关系数式为

其中:x为实际挠度信号;y为分离后的信号。
当相关系数r越接近于1,则表明分离的效果越好。将分离前后的信号代入式(15)计算,结果如表2所示。

表2 各效应分离前后的相关系数Tab.2 Correlation coefficient before and after effect separation
从表2可以看出,日温差效应以及年温差效应的相关系数都接近于1,均实现了很好的分离,但其中年温差端点效应较为明显;长期挠度由于受年温差效应干扰,分离效果相对较差,但总体相关系数都较高,证明了该方法对于各效应分离的有效性。
3 实测桥梁挠度信号各成分分离
3.1 实际工程背景
武汉某斜拉桥主桥为双塔双索面钢箱梁与预应力混凝土箱梁组合型斜拉桥结构,如图12所示。该斜拉桥采用北斗实时在线监测技术,在斜拉桥关键位置布置挠度测点,用来监测桥梁运营状态的安全情况,达到实时监控挠度变化的效果。北斗通过全自动化的高精度监测技术对斜拉桥进行了全年挠度连续的监测,每秒记录1次挠度值。当挠度变化大于阈值时,将会自动产生告警,能为桥梁后期的运营服务提供很好的帮助。测点位置布置如图13所示。

图12 武汉某斜拉桥Fig.12 A cable-stayed bridge in Wuhan

图13 武汉某斜拉桥主桥监测测点布置图(单位:m)Fig.13 Monitoring map of main bridge of a cable-stayed bridge in Wuhan(unit:m)
3.2 实际桥梁挠度分离
选取主跨跨中测点BD12的挠度数据,时间间隔为2017年9月 至2018年8月,每秒采集数据1次,每小时取样1次,BD12挠度曲线如图14所示。

图14 BD12全年挠度数据Fig.14 BD12 annual deflection data
首先,对实测挠度数据用EWT分解;其次,将分解的低频信号进行PCA降维,根据特征值占比大小选取所对应的特征向量重组信号;最终,将重组后的信号输入到FastICA算法,分离出实测挠度中的各效应作用,并且考虑到实际分离信号受到环境因素等的影响,将分离结果拟合,得到BD12全年挠度数据分离结果如图15所示。

图15 BD12全年挠度数据分离结果Fig.15 Separation results of BD12 annual deflection data
由于相邻测点之间受温度效应的影响基本相同,为了验证实测挠度信号分离的效果,取该测点对称处跨中BD35测点的数据进行分离,将各自分离效果进行对比,图16和图17分别为BD35的全年挠度时程和分离后各挠度效应。
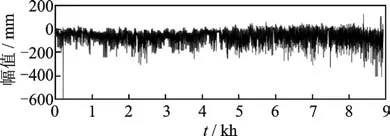
图16 BD35全年挠度数据Fig.16 BD35 annual deflection data

图17 BD35全年挠度数据分离结果Fig.17 Separation results of BD35 annual deflection data
BD12和BD35测点分离效果对比如图18所示,从图中可以看出,BD12与BD35分解的效果相似度较好,证明准确率较高,分离效果好。将此方法与EEMD结合改进PCA算法进行对比,两侧点的分离结果相关系数如表3所示。

图18 对称测点分离结果对比图Fig.18 Comparison chart of separation results of symmetrical measuring points
由表3可知,两测点相关系数均高于0.9,说明基于EWT-FastICA与EEMD和改进PCA方法都能较好地分离出实际桥梁挠度信号中的温度效应,但基于EWT-FastICA算法精度较高。同时由于EWT是直接通过在频谱上自适应切割并构造滤波器,而EEMD则是通过多次添加高斯白噪声和多次求平均,因此EWT相比EEMD计算速度具有较大提升,可显著提高分离效率。为对比计算速度,选择2017年9月至2018年9月实测数据,考虑温度效应周期较长特性,故每小时提取1个数据,共8 928个数据分别运用EWT和EEMD算法进行信号分离,运行速度结果如表4所示。从表4可以看出,EWT运行速度远高于EEMD,而桥梁监测海量数据实时在线分析中,实测桥梁采集频率通常达到几十赫兹甚至几百赫兹,将会产生庞大的数据量,故EWT算法体现出了更大的优越性。

表3 两测点分离后的相关系数Tab.3 Correlation coefficient before and after effect separation
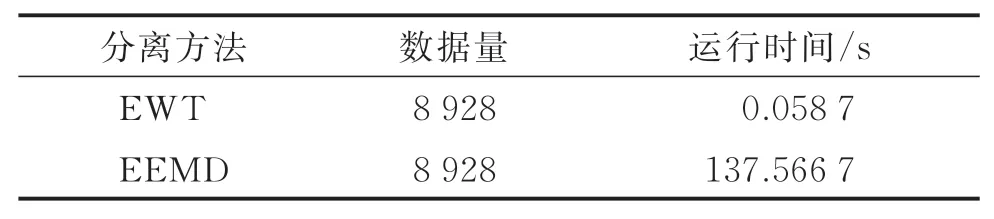
表4 运行速度对比表Tab.4 Running speed comparison table
4 结论
1)采用EWT算法通过在频谱上自适应分割并构造小波滤波器将单通道的混合信号分解成多通道信号,解决了FastICA算法需要观测信号数大于等于源信号数的先决条件。
2)EWT算法相对于EMD和EEMD算法做到了直接分离日温差效应,对于难以分离的长期挠度和年温差,则通过PCA降维提取主元向量后,再基于FastICA算法较好地解决了频率相近信号模态混叠的问题,成功分离出长期挠度与年温差效应。
3)从模拟信号和实测桥梁挠度信号的相关系数以及EWT运行速度来看,EWT算法较EEMD算法极大增强了运算速度,对于桥梁实时在线监测海量数据分析,EWT算法体现出较大的优越性。
