高层建筑顶部围挡结构风荷载试验研究*
2022-11-04马文勇黄铮汉郑德乾张正维
马文勇,黄铮汉,郑德乾,张正维
(1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室 石家庄,050043)
(2.河北省风工程和风能利用工程技术创新中心 石家庄,050043)
(3.河南工业大学土木工程学院 郑州,450001)(4.奥雅纳工程咨询(上海)有限公司 上海,200031)
引言
随着现代社会人口的密集以及城市化进程的加快,超高层建筑呈现越来越多、越来越高的发展趋势[1]。超高层建筑结构频率较低,风荷载对其影响很大[2]。准确估计超高层建筑的风荷载一直都是结构抗风研究的重点问题之一,目前一般可通过风洞试验与随机振动相结合的方法,实现大多数超高层建筑风荷载及风致响应的较准确估计。
笔者采用刚性模型测压风洞试验方法,对具有不同高度顶部围挡的方形断面高层建筑进行研究,探讨顶部围挡高度对结构整体风荷载的影响,以及顶部围挡高度范围内风荷载的分布规律,从而为此类高层建筑整体风荷载取值及顶部围挡部分风荷载取值提供依据。
1 风洞试验概况
1.1 试验设备
试验在石家庄铁道大学的STDU-1风洞试验室低速试验段进行,该试验段截面尺寸为4.4 m×3 m,风速最大可达30.0 m/s。试验采用刚性模型测压试验。压力数据采集系统采用美国PSI公司的DTC系列微型ESP压力传感器和DTC Initium采集系统。
试验时采用的风场为B类风场[17],模型顶部高度(60 cm)处的试验来流风速为10 m/s。采样频率为330 Hz,采样时间为30 s。图1为试验模拟的B类风场平均风剖面及湍流度剖面。
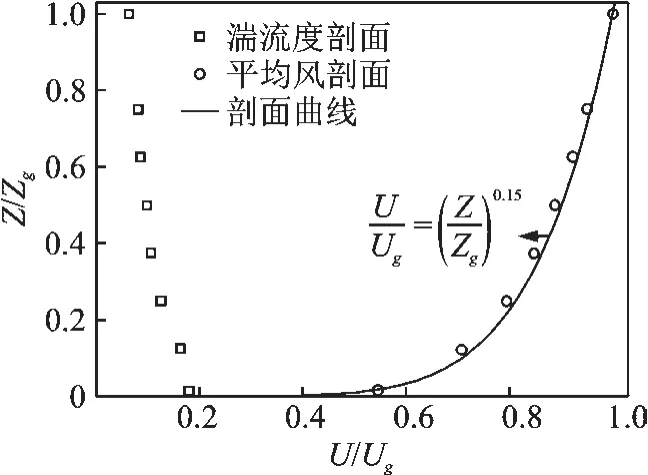
图1 试验平均风及湍流度剖面Fig.1 Experiment wind velocity and trubulence intensity profiles
1.2 试验模型及工况
试验模型采用ABS板制作,模型尺寸为100 mm×100 mm×600 mm,模型缩尺比为1∶500,对应实际高度300 m的超高层建筑。分别考虑了5种顶部围挡高度,即HP为0,20,40,60和80 mm,对应实际的无顶部围挡、10,20,30和40 m高的顶部围挡。采用钢性模型测压试验,模型测点布置如图2所示。

图2 模型测点布置示意图(单位:mm)Fig.2 Arrangement of pressure taps on the model(unit:mm)
沿模型高度共布置10圈测压点,每圈20个测点,当有顶部围挡存在时,在顶部围挡范围内的内外两侧均布置测点,内、外表面测点位置相互对应。在建筑顶面布置4排测点,每排测点4个,共16个测点。模型4个立面按照逆时针分别标记为W,N,E和S,如图2(d)所示。来流风向与W面垂直时为0°风向,风向角φ沿着逆时针方向从0°增大到90°,间隔为5°。
1.3 参数定义
风压系数定义为

其中:Cpi(t)为测点i处t时刻的风压系数;Pi(t)为测点i处t时刻测点的表面风压;P0与Pr为参考高度(建筑顶部高度)处皮托管测得的静压和参考风压;ρ为空气密度;Ur为参考风速,此处取建筑物顶部高度处的来流风速。
采用Cpmean和Cprms表示风压系数的平均值和标准差,称为平均风压系数和脉动风压系数。风荷载体型系数定义为
15) pyamid ['pɪrəmɪd] n.金字塔16) casino [kə'si:nəʊ] n.赌场;俱乐部

其中:Zi为测点所在高度;H为建筑物高度,此处取300 m;α的数值由风场类型决定,此处取0.15。
净体型系数计算公式与极值体型系数计算公式分别为
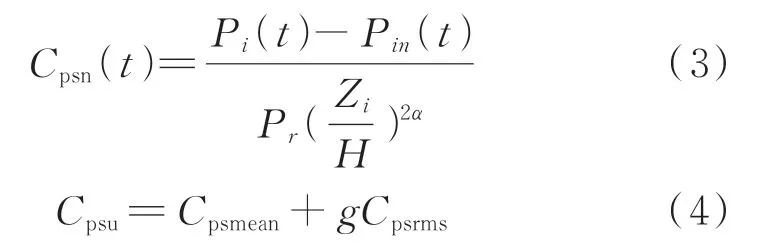
其中:Cpsn(t),Cpsu分别为测点i处t时刻的净体型系数与极值体型系数;Pin(t)为测点i处相对应的内表面测点在t时刻的表面风压;Cpsmean与Cpsrms分别为体型系数的平均值与标准差;g为峰值因子,此处取3.5。
2 顶部围挡对建筑局部风压影响
由于笔者研究的顶部围挡最高为40 m,因此本节主要讨论顶部50 m范围内局部风压的分布以及受顶部围挡的影响规律。本节选取φ=0°以及φ=45°两种典型工况,分析局部风压的分布规律。
2.1 顶部围挡对外表面风压的影响
图3为0°和45°风向角下,建筑外表面250~300 m高度范围内的局部风压系数分布图,从左向右分别为W,N,E和S面。
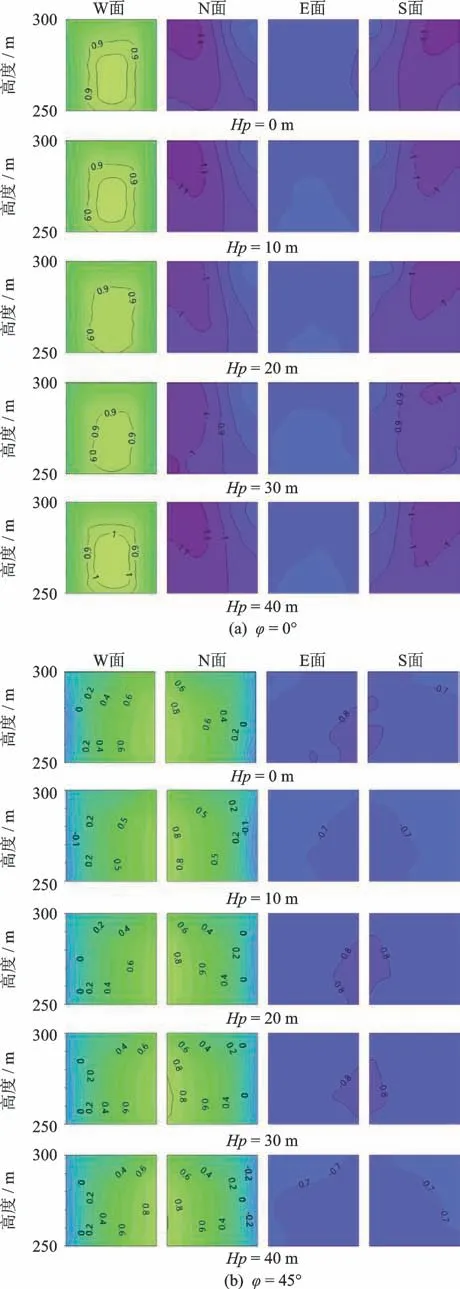
图3 典型风向角下建筑外表面局部风压系数分布Fig.3 Local wind pressure coefficient distribution on the outer faces of the building under typical wind angle of attack
由图3(a)可见,在0°风向角的情况下,建筑迎风面(W面)的正压、背风面(E面)的负压基本不受顶部围挡高度的影响。而在建筑的侧面(N,S面),顶部围挡高度的变化对其风压分布产生了一定的影响,这主要是由于顶部围挡对顶部分离状态的影响所致。具体来说,在不同顶部围挡高度下,建筑侧面边缘位置均出现了负压峰值。其中,围挡高度为20和30 m时的负压峰值略低于其他情况,这是由于顶部围挡高度的变化减弱了该位置处因气流分离而产生的漩涡脱落强度所致。图3(b)表明,45°风向角时,顶部围挡高度的变化建筑外表面的风压分布也几乎无影响,只是E和S面的负压峰值在围挡高度为10和40 m时略有减小。
可见,顶部围挡高度的变化对建筑物外表面的整体风压基本没有影响,仅稍微影响了负压峰值大小。
2.2 顶部围挡对内表面风压的影响
上面分析表明,顶部围挡的出现改变了建筑顶部的气流流动状态,对外表面风压产生了一定影响,同时也将会对建筑物顶面及围挡内表面风压产生影响。图4为0°和45°风向角下建筑物顶面及围挡内表面的风压系数分布,图中左、右侧分别为0°和45°风向角结果。
对于建筑顶面来说,当无顶部围挡时(图4(a)),建筑顶部由于处于流动分离区而表现为负风压,在0°和45°风向角时分别受流动分离产生的柱状涡、三角翼涡的影响,在建筑顶部迎风前缘分别形成了条带形、对称三角形的负压峰值区。当存在顶部围挡时(图4(b,c,d,e)),建筑顶部因围挡的存在改变了其周围流场而使得风压分布发生了显著变化,具体表现如下。
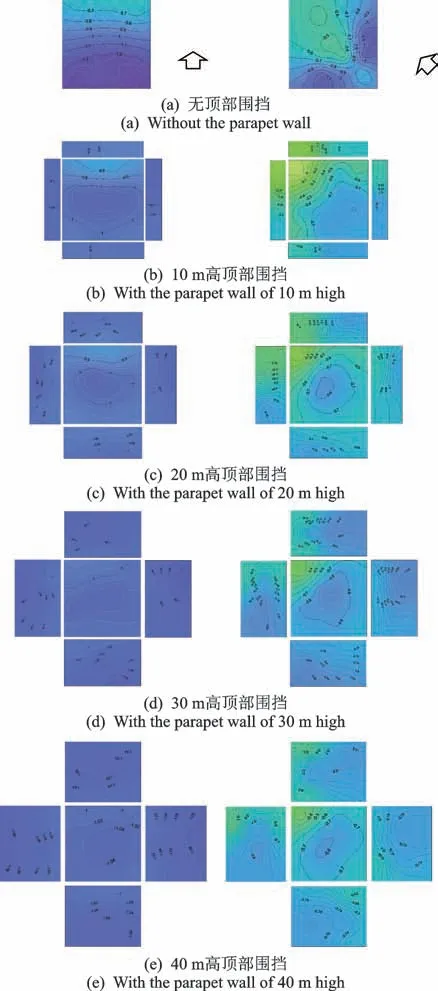
图4 典型风向角下建筑顶部及围挡内表面风压系数分布Fig.4 Wind pressure coefficient distribution on the top surface of the building and the inner surface of the parapet under typical wind angle of attack
1)0°风向角情况下,建筑顶部的负压峰值移动至顶部中心区域且呈现椭圆状分布,负压峰值均明显低于无顶部围挡的情况,说明顶部围挡的存在使得柱状涡从顶面的前半部分移动到了中间部分,漩涡强度呈现中间大、两边小的趋势;随着围挡高度的增加,建筑顶部风压分布渐趋均匀,说明随着顶部围挡高度的增加,气流在建筑物顶面的流动对顶面风压的影响逐渐减小。
2)45°风向角情况下,负压峰值也明显低于无顶部围挡的情况,同时W和N面附近的三角负压峰值区域基本消失,这是由于顶部围挡的存在导致三角翼分离涡基本消失;此外,建筑顶面的负压沿流向对角线逐渐降低,在下游角落部位甚至出现了一小块正压区域。
对于顶部围挡内表面来说,在0°和45°风向角下,内表面均为负压,0°风向角时负压值相对较大但压力梯度相对较小,而45°风向角时负压值相对较小但压力梯度相对较大;随着围挡高度的增加,两个风向角下的负压值的变化均不甚明显。
总体而言,有、无顶部围挡对建筑顶面的风压影响较大,有顶部围挡的情况会降低负压峰值并改变压力分布的规律;顶部围挡高度的增加会缩小顶面风压的变化范围,使顶面风压更为均匀。顶部围挡内表面风压受围挡高度的影响相对较小。
3 局部风荷载取值建议
上述研究表明,顶部围挡对整体风荷载没有影响,但对外表面局部(250~300 m)、顶部以及顶部围挡内表面有着一定的影响。结构抗风中,通常假设结构表面风压服从高斯分布,并据此得到结构设计时的极值体型系数,但实际并非所有区域的风压都服从高斯分布。因此,在进行极值体型系数的计算时,需要将高斯风压与非高斯风压进行区分处理。
3.1 非高斯风压与高斯风压的区分标准
风压脉动的非高斯特性,可采用风压时程的3阶矩(偏度S)和4阶矩(峰度K)表征,其计算公式为

其中:j为风压时程的采样点数,此处取9 900。
考虑到风场的随机特性以及测量中存在的误差,将|S|>0.5且|K|>3.5作为风压非高斯分布的标准,并参照该标准,绘制了0°风向角下不同顶部围挡高度下建筑外表面、顶面与围挡内表面的高斯区与非高斯区,如图5和图6所示,图中阴影部分为非高斯区。由图可见,顶部围挡高度对建筑外表面、顶面以及围挡内表面的非高斯区风压分布区域均有较显著的影响,若不考虑该影响,将影响围护结构极值风压的估计。
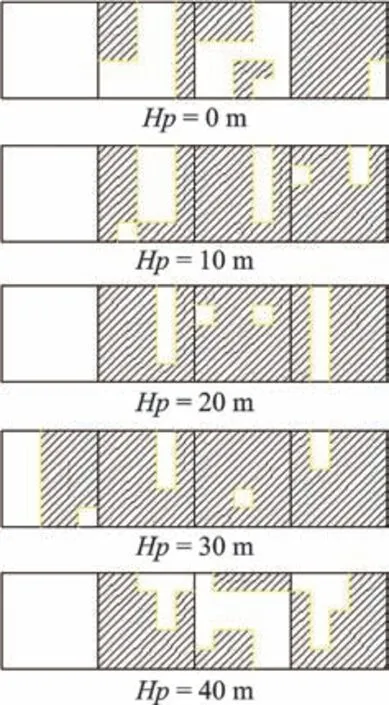
图5 外表面非高斯风压分布区域Fig.5 Sketches of the non-Gaussian wind pressure distribution zone on the outer face

图6 顶面及内表面非高斯风压分布区域Fig.6 Sketches of the non-Gaussian wind pressure distribution zone on the top and inner faces
3.2 局部体型系数取值建议
对于非高斯区域的体型系数的极值,笔者使用极值分布理论对其进行计算[18]。给出了不同顶部围挡高度下围挡内表面、高层建筑顶面和外表面局部区域(250~300 m)的风荷载体型系数,以及顶部围挡的净体型系数取值建议,分别如表1~3所示。其中:表1为建筑顶面可能取得的平均与极值体型系数的最大负值;表2为建筑外表面局部区域可能取得的最大正值体型系数与最大负值体型系数;表3为顶部围挡的净体型系数可能取得的最大正值与负值。

表1 高层建筑顶面体型系数取值建议Tab.1 The suggested value of shape coefficient of the top surface

表2 建筑外表面局部体型系数取值建议Tab.2 The suggested value of shape coefficient of the outer surface
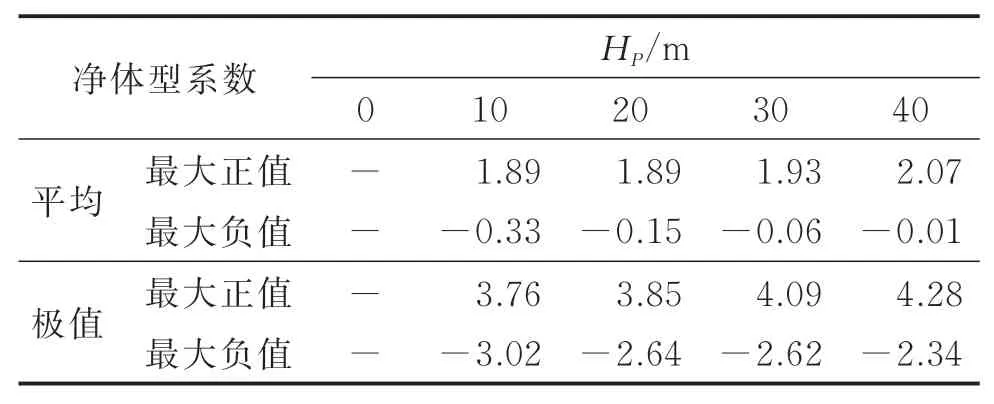
表3 顶部围挡净体型系数取值建议Tab.3 The suggested value of net shape coefficient of parapet
4 结论
1)对于围挡附近的局部风压来说,围挡高度的变化对建筑外表面局部风压并无明显的影响,仅在某些情况下对侧风面的负压峰值有一定影响。
2)对于建筑顶面和围挡内表面而言,顶部围挡的存在会明显改变建筑物顶面局部区域的气流状态,从而降低了建筑顶面的负压峰值及其表面的压力分布。顶部围挡高度的增加会缩小建筑顶面风压的变化范围,使顶面风压更为均匀。围挡内表面风压受围挡高度的影响相对较小。
3)通过划分高斯、非高斯风压分布区域,给出了不同围挡高度下,高层建筑外表面局部区域和建筑顶面,以及围挡表面的风荷载体型系数值,可为该类结构的抗风设计提供参考。
