人行桥人致振动舒适度高效评估*

2022-11-04朱前坤孟万晨张琼马齐飞

振动、测试与诊断 2022年5期

朱前坤，孟万晨，张琼，马齐飞

（1.兰州理工大学防灾减灾研究所兰州，730050）

（2.兰州理工大学西部土木工程防灾减灾教育部工程研究中心兰州，730050）

引言

近年来旅游业迅猛发展，为方便游客通行景区会选择修建大量人行桥，该类桥梁相较于车行桥具有轻质、细长且兼具美观的特点［1］，但其基频远低于车行桥，行人激励下易激发大幅振动［2］，过量振动可能导致行人心理不适，严重时甚至出现晕眩的情况。因此，有必要对人行桥人致振动舒适度进行研究。

国内外学者多采用现场实测和数值模拟方法研究人行桥振动舒适度。冯鹏等［3］将实测的不同工况下人行天桥振动响应与行人感受建立联系，优化了基于振动响应的人行桥舒适性设计。陈波等［4］依据实测结果评价了某大跨斜拉桥的振动舒适度，并指出密集行人行走时桥梁虽然满足舒适度要求，但因其振感明显，行人仍有不适感。

现场实测所得数据能准确反应人行桥动力特性，但对于已开通运营的人行桥，封闭现场进行实测试验可能严重影响交通。相比之下，迅猛发展的有限元模拟技术，为准确、便捷地分析人行桥动力性能提供了可能性。徐欣［5］为评价行人行走时呼日人行悬索桥的振动舒适度，建立悬索桥有限元模型，并依据其在人行荷载作用下的加速度响应进行舒适度评估。邹卓等［6］建立某双塔三跨自锚式人行悬索桥有限元模型，通过时程分析获得该桥加速度响应并进行舒适度评价和减振控制。朱前坤等［7］研究了行人步速对人行桥振动舒适度的影响，研究表明：行人慢速行走时结构舒适度最高，随着步速增大结构振动响应线性增大，当行人步频与结构模态频率一致时人行桥振动响应最大。可路等［8］利用时程分析方法计算了某大跨人行悬索桥在不同人群荷载形式下的振动响应特性，研究发现一定范围内结构峰值加速度响应与行人同步率成正比。对人行桥模型进行时程分析可以准确模拟人行桥动力特性并进行振动舒适度评价，但其耗时和占用巨大计算机资源的缺点依然存在。

为克服该缺点，笔者提出基于AISC Design Guide 11［9］快速评估人行桥人致振动舒适度的FRF方法。首先，对比多种行走工况下FRF方法计算值与试验结果，初步验证了FRF方法计算人行桥跨中最大峰值加速度的准确度；其次，建立某人行悬索桥有限元模型，分别采用时程分析方法和FRF方法计算不同行人行走工况下人行悬索桥跨中最大峰值加速度并进行舒适度评估。结果表明：采用FRF方法进行人行桥人致振动舒适度评估时评估结果偏保守，且比时程分析更高效。

1 人行荷载的力学模型

行走时行人竖向激励荷载呈周期性，Bachmann等［10］深入研究后提出行人激励产生的人行荷载可采用傅里叶级数表示。本研究即利用傅里叶级数模型模拟人行荷载，为使跨中峰值加速度达到最大值，假定行人行走时相位角和步频等参数均保持不变，竖向人行荷载为

其中：F(t)为人行荷载；G为行人的体质量；fp为行人步频；φi为第i阶谐波相位角；αi为第i阶动载因子，是步行荷载傅里叶幅值谱峰值与体质量之比［11］，本研究采用德国人行桥设计指南（EN03-2007）［12］中建议的动载因子。

根据行人行走习惯，行走过程中前足踏地离开时后足已经触地，此时双足同时与地面接触，即出现双足同时踏地的重叠时间段，因此人行荷载加载时需通过式（2）将行人步频fp转换为模型加载的单步周期Ts［13］

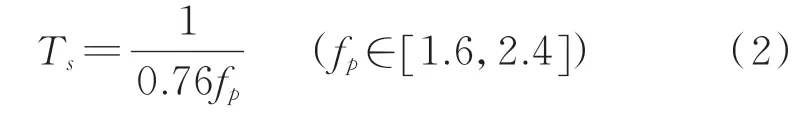
采用APDL编程实现人行荷载加载时，需打开大变形开关和应力刚化开关以考虑轻柔人行悬索桥的几何非线性［14］，并按时间顺序直接将各工况人行荷载的竖向分量依次加载在行走路径对应的有限元网格点（加载点）上，加载频率取1/Ts，这样即可模拟行人行走过程。

2 人行桥峰值加速度快速计算

2.1 频率响应函数方法

AISC Design Guide 11［9］中详细介绍了快速计算人行桥共振响应的FRF方法：对靠近模态振幅峰值（跨中）的单位荷载进行谐响应分析获得FRF幅值，并引入共振累积因子将行人行走路径对结构振动的影响考虑在内，即FRF方法计算的行人与人行桥共振时峰值加速度是最大频响函数峰值FRFmax、动载因子α、行人体质量G和共振累积因子ρ的乘积

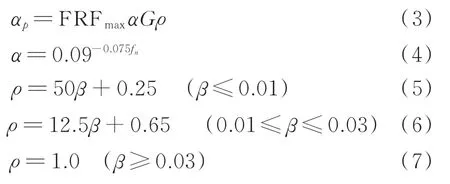
其中：FRFmax为谐响应分析得出的在0～9 Hz范围内的最大频响函数峰值；β为结构阻尼比；fn为结构基频。

2.2 最大频响函数峰值

调用谐响应分析模块对人行桥模型进行扫频分析时，需在靠近结构1阶振型最大位置处施加与人行桥上行人数相同数量的单位荷载。计算时由于谐响应分析只能提取跨中最大位移S，而判断舒适度的指标为峰值加速度，因此需通过式（8）将S转换为跨中最大频响函数峰值FRFmax，再利用式（3）计算得到峰值加速度αp

其中：w为扫频频率。

3 振动舒适度评价

欧美多国制订了详细的振动舒适度评价标准，但各个标准间存在些许差异。瑞典Bro 2004规范和欧洲EN 1990规范均只取一个定值作为标准，英国BS 5400规范仅考虑单个行人荷载，且只取人行桥结构竖向或者侧向1阶固有频率的函数作为限值。相比之下，国际化标准组织ISO-10137［15］对舒适度的评价较为全面，将ISO2631-1［16］中的舒适度曲线乘以60建立舒适度基准曲线，以此作为竖向和侧向舒适度评价标准，但其未划分舒适度等级，导致舒适度评价标准过高。而德国规范EN03—2007［12］参考21世纪以来的研究成果［17］，划分了竖向和侧向舒适度等级标准，如表1所示舒适度等级划分细致，适用于多数建筑，因此笔者依据德国规范EN03—2007对不同工况下人行桥振动舒适度进行评价。

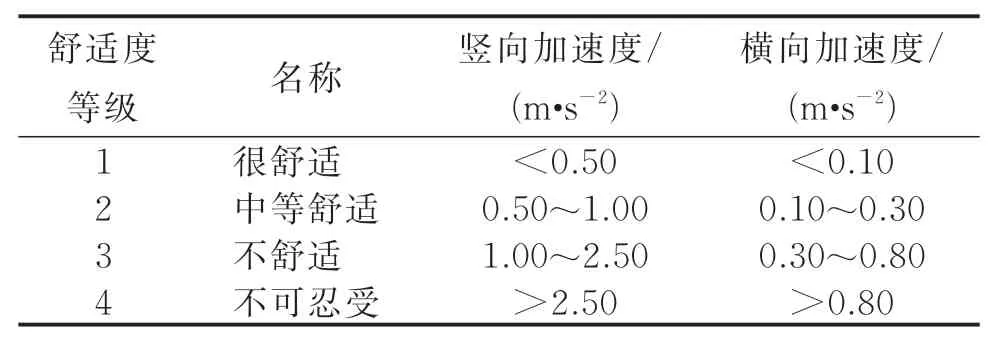
表1 EN03—2007中行人舒适度的评价标准Tab.1 Evaluation standard of pedestrian comfort in EN03—2007

4 简支梁桥试验验证FRF方法

为验证FRF方法计算人行桥共振时跨中峰值加速度的准确度，本节设计多种行人行走工况，对比试验采集和FRF方法计算的各工况人行桥跨中峰值加速度，具体试验方案如下。

选用图1所示钢-玻璃简支梁桥为试验对象，人行桥的基本参数为：主体框架由2根10 m的20a型工字钢和6根1.6 m的20a型工字钢焊接而成；桥面长为10 m，宽为1.6 m，由5块双层夹胶玻璃拼接而成并与钢框架粘接连接，钢框架与地面采用地螺栓锚固连接。

图1 钢-玻璃简支梁桥Fig.1 Steel-glass simply supported beam bridge

对于该尺寸简支梁桥，行人数为8时对应的人群密度为0.5人/m2，已属于德国人行桥设计指南中交通繁忙时的人群密度，因此考虑到安全因素，最大行人数设置为8。与此同时，由于行人正常步频范围为1.6～2.4 Hz［18］，而仪器测定的人行桥基频为4.15 Hz，为使人行桥峰值加速度响应达到最大值，试验中行人步频均取人行桥基频的0.5倍，即取2.08 Hz。

因此，本试验共设置6种工况，分别为单人桥面单列行走，2人、3人、4人、6人和8人桥面双列行走，行人步频均取2.08 Hz，试验过程中同时测量和记录各工况行人体质量。

4.1 试验采集

试验采集仪器包括图2所示的国家地震局941B加速度拾震器（精度为0.1 Hz）和东方所16通道型INV采集分析仪。

图2 加速度采集仪器Fig.2 Acceleration acquisition instrument

试验采集的单人与双人行走工况下人行桥跨中竖向加速度响应如图3所示，双人行走时跨中加速度响应明显大于单人行走，峰值加速度分别为0.240 6与0.448 4 m/s2。

图3 单人与双人行走时跨中竖向加速度响应Fig.3 Vertical acceleration response in mid span of single person and double person walking conditions

4.2 FRF方法计算

简支梁桥有限元模型中桥面、钢梁和链接条件分别采用Shell181，Beam188和Combin14单元模拟，建模完成后采用分块Lanczos法进行模态分析，分析后提取的前3阶振型与模态频率分别为1阶正对称竖弯4.154 9 Hz，2阶扭转6.267 8 Hz和3阶反对称竖弯16.235 Hz，模态频率与简支梁桥实测频率均较为接近。有限元模型如图4所示。

图4 简支梁桥有限元模型Fig.4 Finite element model of simply supported beam bridge

采用FRF方法计算与试验相同的6组工况下简支梁桥跨中峰值加速度，计算时在跨中加载与行人数相同数量的单位荷载并进行谐响应分析，行人体质量取试验中对应工况行人体质量的平均值，阻尼比根据简支梁桥实测取值0.75%。

采用FRF方法计算的单人与双人行走时跨中峰值加速度如图5所示，最大峰值加速度分别为0.291 2和0.541 5 m/s2。

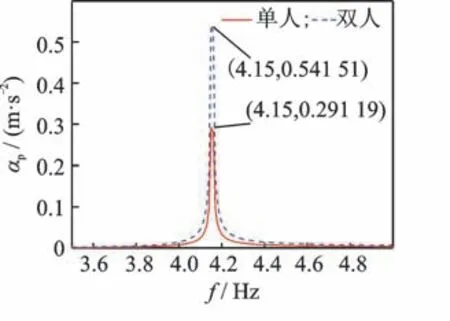
图5 单人与双人行走时FRF计算峰值加速度Fig.5 Peak accelerations calculated by FRF in single and double walking conditions

4.3 结果对比

FRF方法计算的简支梁桥跨中最大峰值加速度为理想共振状态的加速度响应，FRF方法计算值ni大于相同工况的试验采集数据mi。因此，为进一步验证FRF方法计算简支梁桥跨中峰值加速度的准确度，对比mi与ni，对比结果用Pi表示，其值如表2所示。110 mm×70 mm×8 mm的角钢连接。主塔高为19.9 m，上塔柱为2根1.2 m×1 m矩形柱，下塔柱为1.2 m×5 m矩形实体柱。主缆采用成品钢丝索，锚固体系采用重力式地锚形式，风缆和风拉索采用32ZAA6×7+FC1670成品天然纤维芯钢丝绳，均与地面采用锚桩连接。

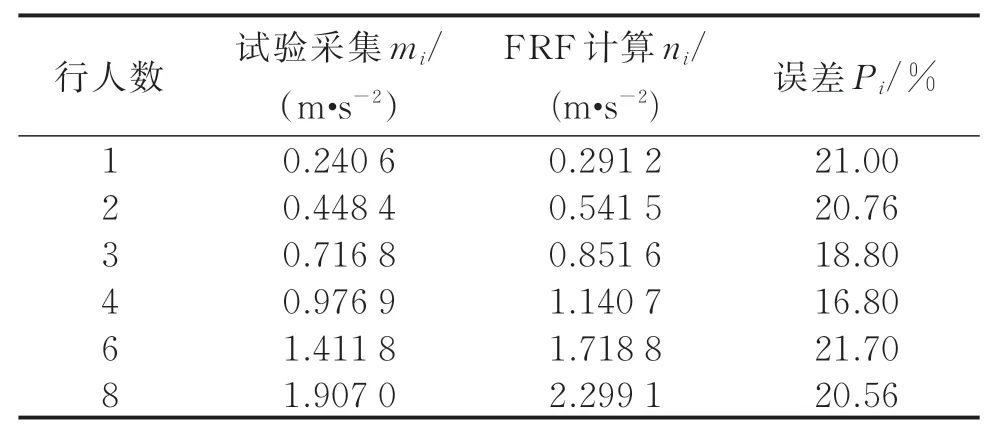
表2 试验结果与FRF计算值对比Tab.2 Comparison of test results with FRF calculated results

由表2可知，通过FRF方法计算的不同工况行人行走时跨中峰值加速度与试验实测采集所得结果相比误差范围为16.80%～21.70%，误差未随着行人数增加出现明显的增长，初步验证了FRF方法计算行人与人行桥共振时跨中最大峰值加速度的准确度。

5 悬索桥模型时程分析验证FRF方法

5.1 人行悬索桥概述

人行悬索桥位于四川盆地西北部，跨越规划河道和货运通道。桥位附近原有一旧悬索桥，由于建成年代久远，破损严重，且不满足水利部门行洪要求，已经拆除。新建人行悬索桥为双塔混凝土地锚式悬索桥，其整体布置如图6所示，净跨径L=120 m，矢跨比F/L=1/12。桥面系采用型钢骨架加混凝土桥面板，主梁节段由横梁、纵梁及平联组成，横梁间距为4 m，由2根36a槽钢组成。为增大桥梁侧向刚度，横梁之间设置4根20a工字钢纵梁，横梁下缘由

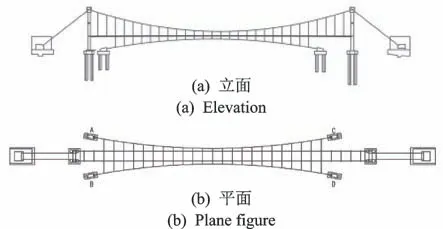
图6 整体布置图Fig.6 General layout

5.2 空间有限元建模

采用离散结构的ANSYS建模方法，加劲梁、纵向分配梁和桥塔模型均采用Beam189单元模拟，该单元可以提供丰富的截面类型选择，能够满足薄壁截面梁单元线性、弹塑性和大变形的分析需求。模拟桥面板时采用Shell63单元，并通过重合桥面板单元节点与加劲梁上旋杆和纵梁单元节点来耦合自由度。在主缆和吊索建模过程中，考虑到2种索的受力特性，选用Link10单元模拟，且打开只受拉选项。人行悬索桥主要构件参数如表3所示，有限元模型如图7所示。

图7 人行悬索桥有限元模型Fig.7 Finite element model of pedestrian suspension bridge

表3 悬索桥主要构件参数Tab.3 Main component parameters of suspension bridge model

5.3 有限元模型的动力特性

人行悬索桥有限元模型模态分析时需施加结构自重将恒载引起的结构内力考虑在内，并采用分块Lanczos法提取前12阶自振频率与振型（见表4），为后续荷载加载提供参考。由表4可知，该桥前12阶自振频率在0.451 1～2.542 8 Hz范围内间隔十分紧密，前3阶竖弯自振频率分别为0.451 1，0.561 0和0.762 0 Hz。

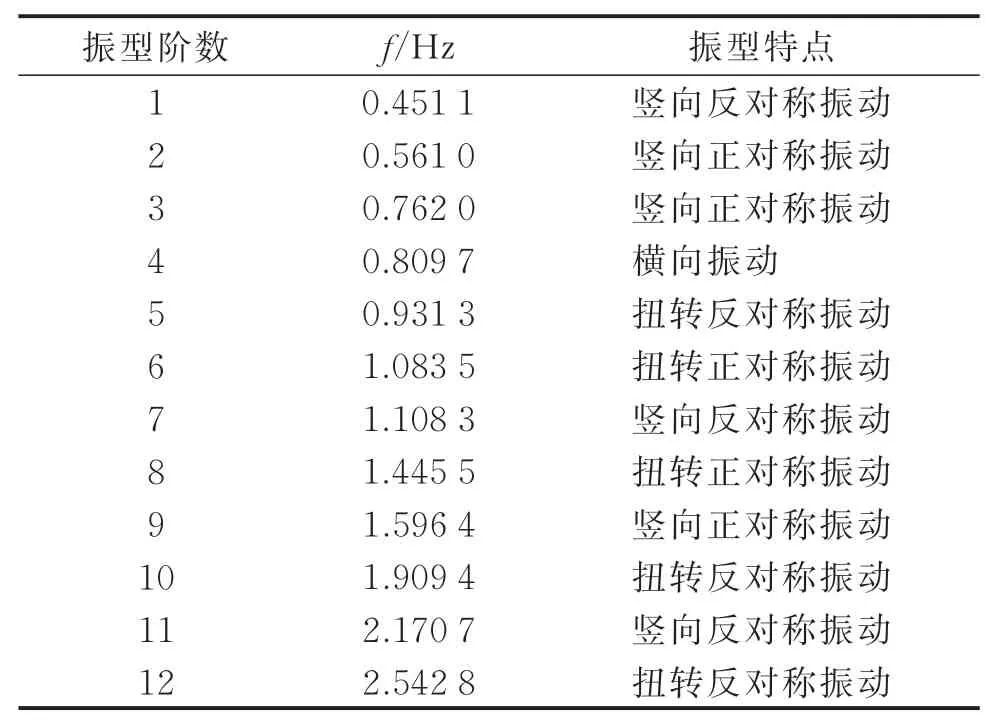
表4 人行悬索桥模型振型与频率Tab.4 Mode of vibration and frequency of pedestrian suspension bridge model

5.4 最不利行人步频

由表4可知，行人步频范围（1.6～2.4 Hz）［18］内存在多个结构模态频率或模态频率的倍频，为评价人行悬索桥正常使用极限状态的振动舒适度，需得到能使行人与结构共振的行人步频。因此，设置18种行人数为30但步频不同的行走工况，步频范围为1.6～2.5 Hz，行走路径与排列方式如图8所示，均为3人并排行走。因本节模拟仅为得到与结构共振的行人步频，此处不再列表展示18种工况的具体参数。

图8 行人行走路径与排列方式Fig.8 Pedestrian route and arrangement

时程分析后提取的各工况跨中峰值加速度如图9所示，对比发现当行人步频取2.1 Hz时，跨中峰值加速度达到最大值，所以该频率为最不利行人步频。考虑双脚重叠后，行人步频为2.1 Hz时加载频率为1.6 Hz，该频率接近结构第9阶模态频率且和2阶模态频率的倍频接近，因此模拟行人行走时的最不利加载频率为1.6 Hz。

图9 步频对跨中峰值加速度的影响Fig.9 The influence of walking frequency on mid-span peak acceleration

5.5 最大峰值加速度计算

5.5.1 时程分析

为准确对比时程分析结果和FRF计算值，设置21种不同行人数的行走工况，行人数由3人递增到108人，步频均为2.1 Hz（加载频率1.6 Hz），行人体质量取70 kg，行走路径与行人排列方式如图8所示。时程后处理提取的30人和60人行走时跨中竖向加速度时程曲线如图10所示，峰值加速度分别为0.480 9和0.839 m/s2。

图10 跨中竖向加速度响应Fig.10 Mid span vertical acceleration response

5.5.2 频响函数计算

采用FRF方法计算21种行人行走工况下人行悬索桥跨中最大峰值加速度，计算时由于缺乏该桥实测阻尼比，参考文献［19］阻尼比取值0.5%，且行人体质量与时程分析中行人体质量保持一致，取值70 kg。采用FRF方法计算的30人和60人行人行走工况峰值加速度如图11所示。

由图11可知，加载频率为竖向2阶自振频率0.56 Hz时出现加速度响应极值，但该频率不在行人步频范围内，因此30人和60人行走时跨中加速度响应最大值为加载频率1.6 Hz时桥梁跨中加速度0.57和1.01 m/s2。

图11 30人和60人行走时FRF计算峰值加速度Fig.11 Peak accelerations calculated by FRF in 30 and 60 people walking conditions

5.5.3 结果对比

21种工况的时程分析结果和FRF计算值如图12所示，为进一步验证FRF方法计算峰值加速度的准确度，利用式（9）对比各工况的时程分析结果mi与FRF计算值ni，对比结果如图13所示。

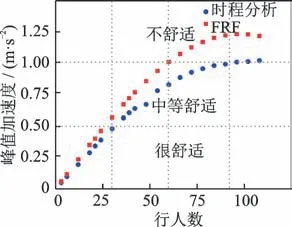
图12 各工况跨中峰值加速度与舒适度评价Fig.12 Mid span peak acceleration and comfort evaluation under various working conditions

图13 时程分析与FRF计算结果对比Fig.13 Comparison of time history analysis and FRF calculation results

由图12，13可知，尽管FRF方法计算的各工况峰值加速度值均高于时程分析计算结果，且加速度差值随着行人数的增加逐渐增大，但FRF计算值与时程分析计算结果平均存在20.71%的误差，且误差在正负两倍标准差内的置信度为95%，认为FRF计算值与时程分析结果误差小且稳定分布在20%左右。因此，对比时程分析结果，FRF方法计算的跨中峰值加速度有较高且稳定的准确度。

依据德国规范EN03―2007［12］对两种方法计算的跨中峰值加速度进行振动舒适度评价，评价结果如图12所示，发现21种工况中有14种工况的舒适度评价结果相同。行人数为30时，依据FRF方法计算值评价的舒适度为中等舒适，依据时程分析结果评价的舒适度为很舒适。行人数在60人到90人之间的6个工况，依据FRF计算值进行舒适度评价时舒适度为不舒适，而依据时程分析结果评价的舒适度为中等舒适。因此，与时程分析相比，依据FRF方法计算结果进行舒适度评价时结果偏保守。

5.5.4 计算速效对比

分别在便携笔记本和DELL服务器中运行人行悬索桥的时程分析与FRF方法，计算不同行人行走工况时消耗的平均时间和硬盘空间，笔记本计算速效对比和服务器计算速效对比如表5和表6所示。

由表5和表6可知，相较于时程分析方法，FRF方法计算最大峰值加速度更加高效，运算时间节省94.89%，占用的硬盘空间节省87.2%。