翼面热静气动弹性的流固热交错迭代耦合分析*
2022-11-04常斌黄杰姚卫星
常斌,黄杰,2,姚卫星,2
(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)
(2.南京航空航天大学飞行器先进设计技术国防重点学科实验室 南京,210016)
引言
翼面的静气动弹性是飞行器设计必须考虑的问题,它涉及到气动力与结构弹性变形之间的耦合。随着飞行器速度越来越快,气动加热引起翼面结构温度升高[1-3],导致翼面结构刚度发生变化[4-5],并由此提出了热静气动弹性的问题,热静气动弹性的研究对高超声速飞行器的设计至关重要。
最早的高超声速翼面热静气动弹性分析方法假设翼面结构具有均匀的温度场分布,分析不同温度下的翼面热刚度,并在此热刚度下进行翼面的静气动弹性分析。随着气动热分析技术研究的深入,一些学者采用以Eckert参考焓法[6]为代表的工程近似方法分析翼面气动热问题,将分析获得的翼面热流作为边界条件,并通过有限差分法等求解热传导方程获得翼面温度场分布,再研究翼面的热刚度和热静气动弹性[7-8]。以上传统翼面热静气动弹性分析方法的计算精度较差,已无法满足现代及未来高超声速飞行器热静气动弹性的分析要求。传统方法最主要的缺点是未考虑结构温度场对气动热的反馈效应。实际上气动热与结构温度场之间存在着强烈的耦合效应,但传统分析方法仅考虑了气动热引起的结构温度场升高,而未考虑翼面温度升高后对壁面热流的影响。
随着计算流体力学(computational fluid dynamics,简称CFD)、数值传热学(numerical heat transfer,简称NHT)及计算结构动力学(computational structural dynamics,简称CSD)的发展,近年来一些学者通过CFD和NHT之间的耦合分析求解结构温度场,研究热环境对结构热刚度的影响,最后通过CFD和CSD之间的耦合分析求解热静气动弹性响应[9-10]。该方法分2步计算,能获得精确的壁面热流和结构温度场,并准确评价翼面结构热刚度,具有计算精度高的特点。由于CFD与NHT的耦合以及CFD与CSD的耦合需要进行2次CFD计算,故该方法还存在计算效率较低的缺点。此外该方法也无法考虑翼面变形对气动热带来的影响,因此需要一种兼顾计算精度和计算效率的耦合分析方法。
笔者提出了一种针对高超声速翼面热静气动弹性的流固热交错迭代耦合方法,其主要特点是能考虑翼面变形对气动热的影响,且不需要像传统热静气动弹性耦合方法分2步求解,并且利用该方法进行了典型高超声速翼面热静气动弹性问题的分析。
1 流体和结构传热控制方程
流体动力学的控制方程为Navier-Stokes方程,
其在直角坐标系下的积分形式为
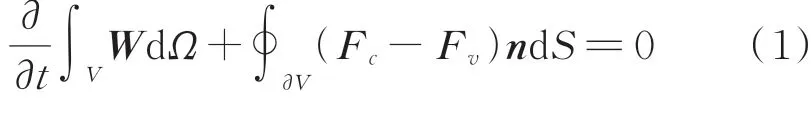
其中:W为守恒向量;Fc为 对 流 通量;Fv为黏性通量;dS为控制体V的边界面;n为边界面dS的 外法线单位向量。
Navier-Stokes方程中对流通量Fc的空间离散采用AUSM+格式[11],黏性通量Fv的空间离散采用中心差分格 式,湍 流模拟采用Menter′s SSTk-ω两方程模型[12],时间推进采用LU-SGS格式[13],且采用聚合多重网格法[14]加速收敛。
翼面结构传热分析的控制方程为
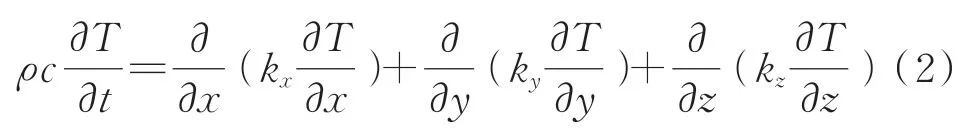
其中:kx,ky和kz分别为材料在x,y和z方向的导热系数;ρ和c分别为结构材料的密度和比热容。
翼面结构传热分析的边界条件包括壁面热流Qw和壁面辐射热流Qr,其表达式为

其中:ε为表面发射率;σ为玻尔兹曼常数;Tw为壁面温度。
笔者采用有限元法进行翼面结构传热及变形的分析。
2 交错迭代耦合分析方法
高超声速飞行器做定常飞行时,翼面所受的气动力和气动热均稳定,其可通过数值方法计算同时得到,因此统称为气动环境。翼面热静气动弹性分析中主要存在2种耦合效应:①气动环境中的气动热与结构传热之间的耦合效应,当气动热作用于翼面时,翼面结构温度升高,翼面结构温度的升高导致边界层内气体与壁面温度的梯度减小,即气动热效应将减弱;②气动环境中的气动力与结构变形之间的耦合效应,当气动力作用于翼面时,翼面产生变形,变形会造成气动力重分布。此外,翼面变形也会造成壁面热流的重分布,且热环境还会影响翼面结构刚度(材料刚度和热应力引起的附加几何刚度),进而影响结构变形。笔者考虑以上所述的耦合效应,而忽略其他次要因素,建立了如图1所示的翼面热静气动弹性分析耦合模型。

图1 耦合模型Fig.1 Coupled model
根据图1中的耦合模型,笔者采用流固热交错迭代耦合方法进行高超声速翼面热静气动弹性的研究,交错迭代耦合方法如图2所示,图中的i为耦合迭代步。采用CFD方法进行翼面气动力和气动热的计算,采用NHT方法进行翼面结构温度场的计算,采用CSD方法进行翼面结构变形的计算,其中CFD方法基于有限体积法,而NHT和CSD方法均基于有限元法。流固热交错迭代耦合方法的基本假设和特点如下:

图2 交错迭代耦合方法Fig.2 Staggered iterative coupled method
1)在流场计算过程中(气动力和气动热)翼面结构参数(结构变形和壁面温度)保持不变,同理在结构计算过程中(结构变形和壁面温度)翼面气动环境(气动力和气动热)保持不变;
2)只需进行一次耦合分析即可获得翼面气动力、壁面热流、温度场和结构变形的全部稳态结果。
翼面热静气动弹性的交错迭代耦合方法分析流程如图3所示,其主要步骤为:

图3 交错迭代耦合分析流程Fig.3 Staggered iterative coupled analysis process
1)首先建立CFD,NHT和CSD数值分析模型,通过CFD分析获得初始气动力和壁面热流;
2)进行第i步的CFD计算,将计算获得的气动力Fi和壁面热流Qi分别传递给CSD模型和NHT模型;
3)进行第i步的NHT计算,将计算获得的翼面结构温度场Ti传递给CSD模型,并更新翼面结构刚度;
4)进行第i步的CSD计算,将获得的翼面表面位移Uwi及表面温度Twi传递给CFD模型,并进行流体网格变形;
5)若翼面结构变形和温度场均收敛,则结束迭代。否则重复步骤2~4,直至结果收敛,结束分析。
由于流场和结构的网格尺寸相差较大,耦合变量需要在耦合面上通过插值算法实现数据的传递。笔者采用文献[15]中的基于控制面的双向映射插值方法进行壁面热流、壁面温度、气动力以及翼面变形的数据传递。此外为了加速收敛,在流场计算中引入了子迭代。
目前还没有热静气动弹性的标准试验,且翼面热静气动弹性分析的核心是精确计算气动热和结构温度场,故笔者采用NASA的高超声速空心圆管模型[16]进行气动热和结构温度场计算精度的验证。文献[17]已经进行了空心圆管模型的耦合计算,外壁面热流和温度分布的计算结果与试验结果吻合良好,验证了计算精度。
3 翼面热静气动弹性分析
3.1 计算模型
笔者采用小展弦比翼面进行热静气动弹性的分析,其平面和剖面如图4所示。小展弦比翼面来源于F104战斗机机翼,图中参数C为翼根弦长。假设高超声速自由来流马赫数从6增加至9,飞行高度为10 km,攻角为0.5°,且整个翼面结构的初始温度为300 K。划分了流场的结构网格,网格量约为80万,为了保证翼面热流的计算精度,壁面第1层网格高度小于1×10-5m,图5为CFD计算网格及结构传热和变形分析的翼面结构表面计算网格。笔者假设翼面前缘为耐高温碳/碳复合材料结构,其导热系数、弹性模量和热膨胀系数分别为42 W/(m·K),95 GPa和4×10-6K-1。翼面其他部位采用TA7耐高温钛合金结构,材料密度为4.4×103kg/m3,但材料导热系数、弹性模量和热膨胀系数均与温度相关,可参考文献[15]。文献[15]进行了翼面的CFD和NHT耦合计算,获得了结构温度场,并研究了在热环境下弹性模量和热应力对模态的影响。笔者考虑了气动热、气动力、结构传热和结构变形,是典型的热静气动弹性问题。翼面外表面有高辐射率的涂层,其发射率为0.85。此外流场计算中引入了子迭代,子迭代步数设置为30。
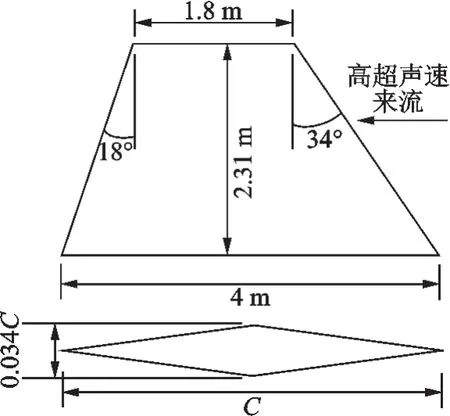
图4 小展弦比翼面的平面和剖面Fig.4 Platform and cross-sectional views of the low aspect ratio wing
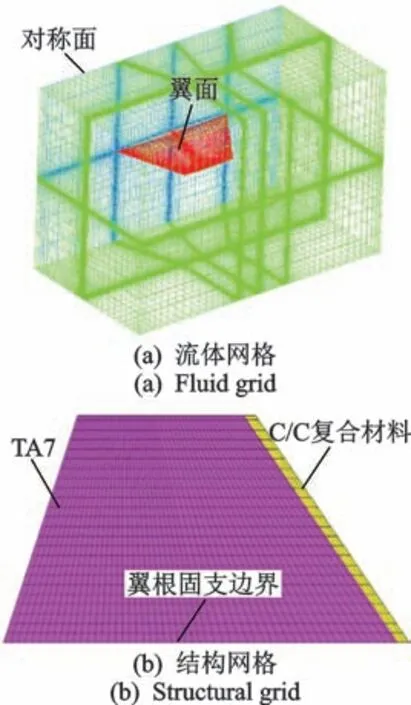
图5 计算网格Fig.5 Computational grids
3.2 翼面热环境及热静气动弹性变形
笔者通过流固热交错迭代耦合方法获得了马赫数从6增加至9的计算结果。翼面结构温度场和翼面变形均在25步以内达到收敛状态。图6给出了其表面温度云图,结果表明在不同马赫数下计算获得的翼面结构温度分布情况相似。由于翼面前缘当量半径很小,故该部位的壁面热流和温度最高,且往下游翼面结构温度逐渐降低。此外马赫数从6增加到9,翼面结构最高温度从1 525.4 K上升到2 163.3 K,翼面结构最低温度从824.9 K上升到996.2 K。

图6 不同马赫数下翼面结构温度场Fig.6 Temperature field of wing for different Mach number
热静气动弹性与常规静气动弹性的主要区别是热环境下翼面结构刚度会发生变化。首先,高温会直接影响材料的弹性模量,针对本研究采用的TA7耐高温钛合金材料,温度越高材料的弹性模量越低;其次,高温下翼面结构会膨胀,结构受到约束及内部温度分布不均匀时均会产生热应力。热应力的本质是预应力,预应力会造成几何非线性现象,即翼面结构会产生附加的几何刚度。因此,必须综合考虑热环境造成的材料弹性模量的降低及热应力引起的附加几何刚度才能准确计算翼面变形。
笔者通过流固热交错迭代耦合方法分析获得了马赫数从6增加至9的翼面法向(垂直于翼面方向)的热静气动弹性变形,其热环境下翼面法向位移如图7所示,结果表明在不同马赫数下翼面热静气动弹性变形情况相似。图8为300 K和热环境下翼面最大厚度处的法向位移沿展向的分布情况,图9为300 K和热环境下翼面法向最大位移随马赫数的变化情况。
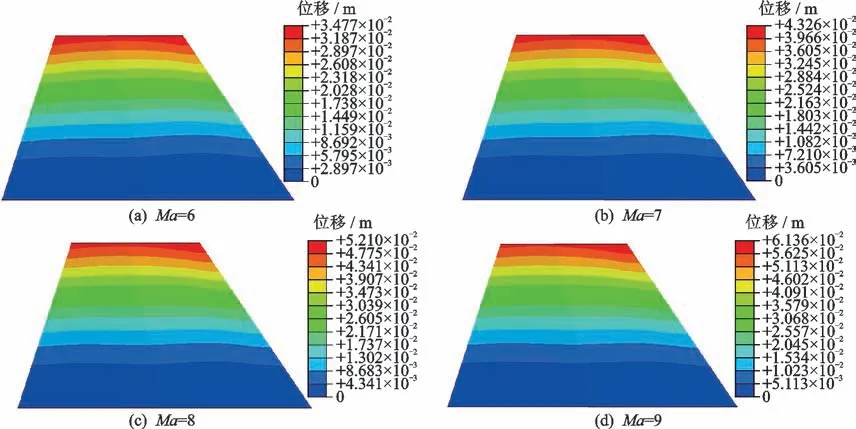
图7 热环境下翼面法向位移Fig.7 Normal displacements of wing under thermal environments

图8 翼面法向位移沿展向分布情况Fig.8 Normal displacements of wing along the spanwise direction
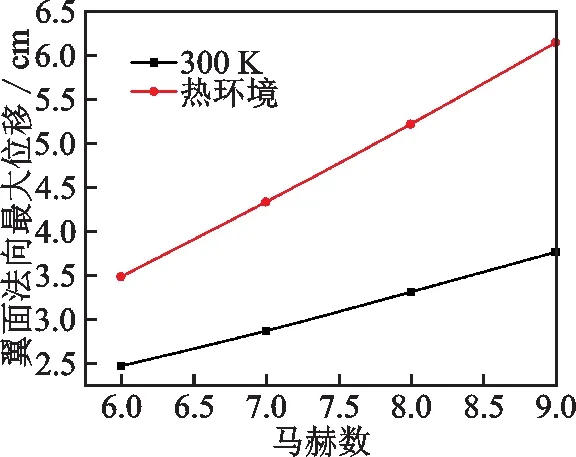
图9 翼面最大法向位移Fig.9 Maximum normal displacements of wing
由以上分析结果可知,随着马赫数的增加,翼面变形越大。此外在相同马赫数下,考虑热效应时翼面法向位移明显大于300 K时的分析结果。马赫数为6,7,8和9时,热环境下翼面法向最大位移分别比300 K时大41.05%,51.10%,57.64%和63.28%,即马赫数越大,考虑热环境和不考虑热环境获得的翼面变形量之差越大。这是由于热环境下翼面结构刚度降低了,且马赫数越大翼面结构刚度下降越快,造成变形量迅速增加。
综上所述,进行高超声速翼面静气动弹性分析时必须考虑其热效应,热环境导致翼面结构刚度降低,造成翼面变形高于常温下的结果,应给予足够重视。
4 结论
1)提出了一种针对高超声速翼面热静气动弹性的流固热交错迭代数值耦合方法。该方法充分考虑了气动环境(气动力和气动热)与结构变形之间的耦合、气动热与结构温度场之间的耦合以及温度场对结构刚度的影响,能克服传统热静气动弹性耦合方法中未考虑翼面变形对气动热影响的缺点。
2)进行了翼面热静气动弹性分析,针对本研究的翼面结构形式和来流状态,热环境造成了翼面结构刚度下降,从而导致热环境下翼面法向最大位移比300 K时增加了40%以上,且马赫数越大,两者之差越大。因此,热环境对高超声速翼面的静气动弹性变形影响明显,在分析时必须考虑其影响才能获得准确的分析结果。
