依据主成分和协整性的大坝变形奇异诊断*

杨光，李姝昱，孙锦

（1.华北水利水电大学水利学院 郑州，450046）

（2.河海大学水文水资源与水利工程科学国家重点实验室 南京，210098）

（3.黄河水利科学研究院 郑州，450003）

（4.华北水利水电大学测绘与地理信息学院 郑州，450046）

引言

变形是大坝服役性态变化的综合反映，是衡量结构安全与否的重要标志。科学地分析变形原位监测信息，不仅是现行规范的要求，而且是监控大坝安全的有效手段［1-2］。受多种因素的干扰，原位监测资料中常包含奇异成分，表现为测值在某时刻或某时段的异常突跳，即孤立型或斑点型奇异成分。若未有效诊断出监测资料中的奇异成分，极可能影响大坝安全监控结论的客观性，造成虚假报警或将危险状况遗漏。尤其对于运行多年的老坝，监测仪器的性能和稳定性较差，此问题尤为突出。因此，提出科学的大坝变形原位监测数据奇异成分诊断方法，具有重要的理论意义和应用价值。

大坝变形原位监测数据奇异成分诊断包括辨识和估计2个环节。常规的辨识方法有［3-4］：①过程线法，通过绘制变形过程线，直观辨识奇异成分；②假设检验法，如拉依达检验、狄克松检验。传统的估计方法包括［3-4］：①忽略法，若无法还原或难度较大，可直接忽略；②似然估计法，如临近插值、三次Hermite插值、统计模型及自回归模型。总体来看，常规诊断方法大多以变形时间序列为分析对象，无法有效地捕捉多测点间隐含的变形关系，且主观性较强，易误诊。

相较于1维时间序列，多维数据序列具有信息量丰富、自由度高及稳定性强的优势，包含了隐匿、新颖及有潜在价值的信息［5］。PCA［6-9］和CA［10-12］是两种多维数据特征挖掘方法。PCA可将多维数据序列投影到不同方向上，得到主要规律和无法解释成分，其中无法解释成分包含了奇异数据、噪声等。对于大坝上临近的监测点，变形监测序列存在关联性，若未出现超标准洪水、极端天气等非常规状况，某监测点变形数据异常，其他临近点的数据未见异常，则可判定该监测点的变形数据奇异。CA刻画了多维数据序列的长期关系，若未发生非常规状况，多测点变形监测序列的协整关系一般不会明显改变，据此可实现对奇异成分的估计。

综上所述，笔者利用多维数据的优势，基于PCA，研究奇异成分辨识准则；依据CA，探究奇异成分似然估计模型；在此基础上，结合实际工程，检验PCA-CA方法的有效性。

1 诊断方法

1.1 奇异成分辨识

依据2维数据格式，建立大坝变形原位监测数据集合，即

其中：m为监测点总数；n为监测时长；xi，xj分别为测点i和j的监测序列；xki，xkj分别为测点i和j在k时刻的监测值。

PCA辨识步骤如下。

1）分析环境量监测资料，若未发生非常规状况，则执行后续步骤。

2）对矩阵X进行标准化，得到矩阵,为标准化的xi，为 标 准化的xj。相关系数矩阵R为

其 中：rij为和的相关系数，计算公式为rij=(i，j=1，2，…，m)；和为标准化 的xki和xkj。

3）计算相关系数矩阵R的特征向量矩阵P和特征值矩阵λ，计算公式为

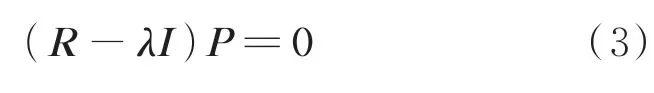
其中：0为m阶零矩阵；I为m阶单位矩阵。

式（3）中的P和λ分别表示为

其 中：λi为矩阵R的第i个特征值，满足λ1≥λ2≥…≥λm；pi为λi对应的特征向量。

4）建立n×m矩阵T，记为(t1，t2，…，tj，…，tm)

5）计算第j项tj(j=1，2，…，m)对原始序列X的解释能力ej

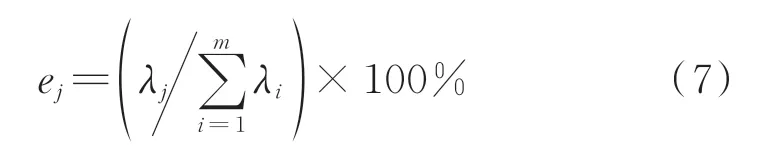
由式（7）可知：①前j项对X的累积解释能力为，所有m项的累积解释能力为1；②e1≥e2≥…≥em，即t1→tm对X的解释能力逐渐变弱；③e1越大，X的主要规律越明显。因此，为保证PCA辨识精度，要求e1尽可能大。

6）建立SPE统计量。由于P为正交矩阵，满足

则式（6）可变换为

k时刻SPE统计量记为SPEk，计算公式为

7）依据假设检验，在显著性水平α下，建立SPE控制限［13-14］，记为SPEα，即

假设检验中α常取为0.05或0.01，即接受原假设时，正确的概率为95%或99%。

8）图1为SPE统计与控制限的关系。若SPEk未超过SPEα，如图1（a）所示，则不存在奇异成分；若SPEk在某时段超过SPEα，如图1（b）所示，则为斑点型奇异；若SPEk在某时刻超过SPEα，如图1（c）所示，则为孤立型奇异。若奇异，则执行步骤9。

图1 SPE统计量与控制限的关系Fig.1 Relationships between SPE and its control limit

9）测点j对k时刻SPEk超过SPEα的贡献度用CSPEkj统计量表征，即

CSPEkj越大，则测点j对k时刻SPEk超限 的贡献度越大，而CSPEkj最大处，即为存在奇异成分的测点。

1.2 奇异成分似然估计

假设m个变形监测序列中有f个存在奇异成分，记为x′1…x′h…x′f，剩余p=m-f个不存在奇异成分，记为。CA似然估计步骤如下。

1）建立多测点变形原位监测序列的协整模型，即

其中：cqg为的系数；aq为的最高次数，依据变形散点关系确定；ε为余量序列。

2）应用逐步回归算法，确定式（14）的系数cqg，得到余量序列ε。

3）利用ADF检验［15-16］，测试ε的平稳性。若ε平稳，则协整，执行步骤4；若非平稳，则不协整，此时算法不适用。

4）利用式（14），估计x′h的 奇 异成分，修正矩阵X。

5）利用PCA准则，辨识矩阵X中是否仍然存在奇异成分，若存在，重复执行步骤1～4，直至无奇异成分。

2 工程实例分析

2.1 工程实例1

陈村拱坝最大坝高为76.3 m，设计汛限水位为117.0 m，汛后正常高水位为119.0 m，500年校核水位为123.8 m，5 000年校核水位为126.1 m，保坝水位为127.7 m。18正下（1号测点），26正下（2号测点）和29倒（3号测点）测点的位置如图2所示，径向变形过程线和置信区间法计算结果如图3所示，环境量过程线如图4所示。

图2 29#，26#和18#坝段垂线监测点Fig.2 Vertical monitoring points of the 29#,26# and 18#dam sections

依据水压-温变-时效（hydraulic-seasonal-time，简称HST）模式［17］，建立变形监控模型，HST模型精度如表1所示。由表可知，3个模型的复相关系数R均大于0.95，且标准差S较小，拟合精度较高。应用置信区间法［17］，评判变形变化是否正常，2S为正常与基本正常的临界值，3S为基本正常与异常的临界值。由图3（b）～（d）可知：①1号测点未超出3S，在42天超出了2S，未报警；②2号测点未超出3S，在23天超出了2S，未报警；③3号测点在2天超出了3S，且在148天超出了2S，发生报警。

表1 HST模型精度Tab.1 Accuracy of the HST models

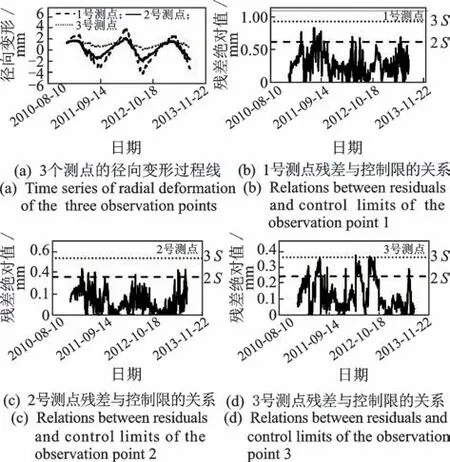
图3 径向变形过程线和置信区间法计算结果Fig.3 Time series of radial deformation and calculation results of confidence interval approach

由图4可知，该时段未出现非常规水位和温度状况，因此受奇异成分影响，监控模型虚假报警。利用本研究方法，诊断3个测点的奇异监测数据。经计算，e1为95.23%，且余量序列协整，诊断出的奇异监测数据有斑点型和孤立型，如：1号测点的变形监测值在2012-07-11为孤立型奇异；3号测点的测值在2011-05-25至2011-07-19期间为斑点型奇异。

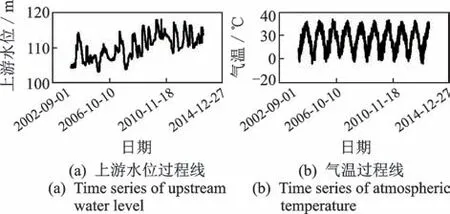
图4 环境量过程线Fig.4 Time series of environment factors

重新建立监控模型，结果显示：①1号测点在3天超出了2S，未超过3S；②2号测点在5天超出了2S，未超 过3S；③3号 测点 在14天超 出 了2S，未超过3S。

2.2 工程实例2

斑点型奇异可视为孤立型奇异的集合，因此孤立型奇异辨识和斑点型奇异估计具有分析的代表性。结合锦屏一级拱坝3个垂线点PL11-3，PL11-4和PL13-3的径向变形监测资料，通过人为构造奇异成分［18］，检验PCA-CA方法的性能。测点布置如图5所示，图6为径向变形原位监测过程线。

图5 11#，13#坝段垂线监测点布置Fig.5 Vertical monitoring points of the 11# and 13# dam sections

图6 PL11-3，PL11-4和PL13-3的径向变形监测序列Fig.6 Time series of radial deformation of PL11-3,PL11-4 and PL13-3

2.2.1 PCA辨识性能分析

图7为PCA方法的诊断结果。依据PCA辨识步骤1～5，得到了t1～t3效应量，如图7（a）～（c）所示，测点变形时间序列的相关系数矩阵如表2所示，t1～t3的特征值、解释能力以及累积解释能力如表3所示。依据步骤6，可得到SPEk过程线，在执行步骤7时，α取为0.01，计算得到控制限SPE0.01=0.11，由图7（d）可知，SPEk＜SPE0.01，因此3个测点的变形原位监测数据不包含奇异成分。

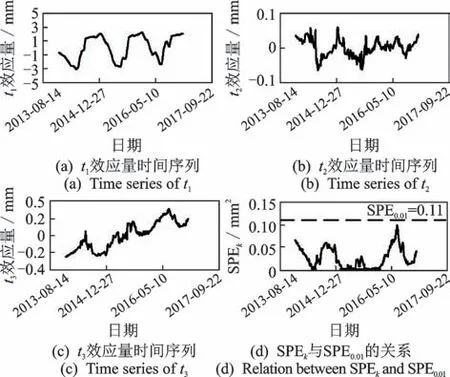
图7 PCA方法的诊断结果Fig.7 Diagnosis results of the PCA method

表2 相关系数矩阵Tab.2 Correlation coefficient matrix

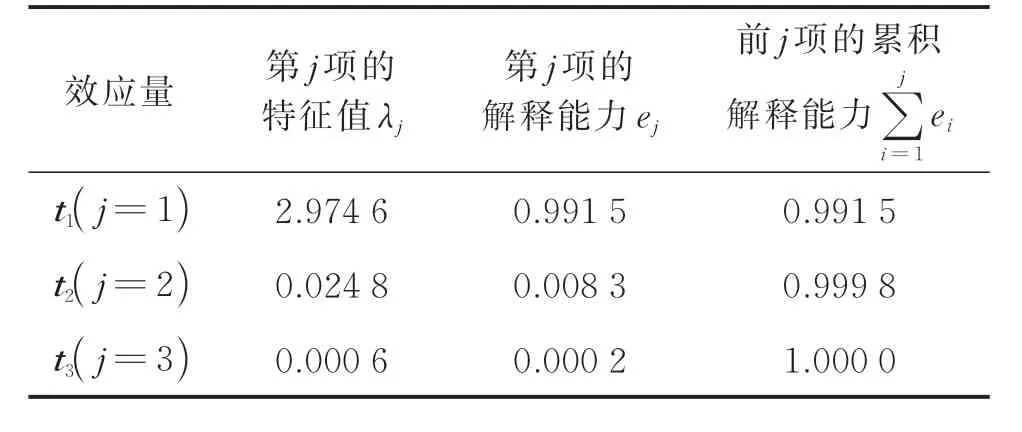
表3 特征值、解释能力及累积解释能力Tab.3 Eigenvalues,explanatory capabilities and accumulated explanatory capabilities

PL11-4测点在2014-10-03的径向变形监测值为39.4 mm，将其构造为不同程度的孤立型奇异成分，记作0#～6#情况，分别为39.6，39.9，40.4，40.9，41.4，42.4和43.4 mm。图8为1#～5#情况下SPEk与SPE0.01的关系图，图9为1#～6#情况的CSPE统计量。由图8可知，在2#～5#情况下，SPEk超过了SPE0.01，且 从 图9可 以 看 出，在2#～6#情 况 下，PL11-4测点的CSPE统计量明显高于PL11-3和PL13-3，因此2#～6#可判定为孤立型奇异成分。表4比较了PCA准则、拉依达准则、狄克松准则和t准则的性能，可以看出，4种方法分别可辨识出相对误差为3.81%，7.61%，7.61%和5.08%的孤立型奇异成分。

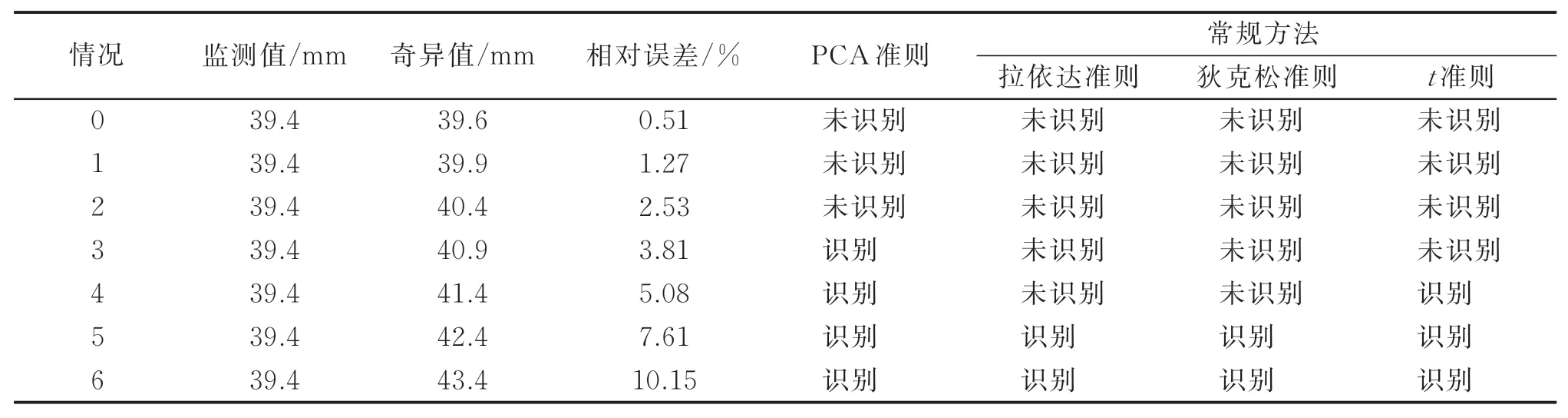
表4 4种方法性能对比Tab.4 Performance comparison of four methods

图8 1#～5#情况下SPEk与SPE0.01的关系Fig.8 Relations between SPEk and SPE0.01 under 1# case～5# case

图9 1#～6#情况的CSPE统计量Fig.9 CSPE statistics of 1# case～6# case

2.2.2 CA估计性能分析

假设PL11-4测点在2016-07-15至2016-09-15期间的变形监测数据为斑点型奇异，利用2014-01-01至2016-07-14的原位监测资料建立协整模型，对奇异成分进行估计。图10为3个测点径向变形散点关系。由图可知，式（16）的最高次数aq均取1，利用逐步回归法，可得

图10 PL11-3，PL11-4和PL13-3测点径向变形散点关系Fig.10 Scatter relations among radial deformation of PL11-3,PL11-4 and PL13-3

图11为CA方法的估计结果。PL11-4的监测值、拟合值和余量序列如图11（a）所示，复相关系数为0.997 1。ADF检验结果显示：t统计量的值为-2.724 4，1%和5%两个显著性水平的临界值分别为-2.400和-2.150，因此t统计量小于临界值，即原假设均被拒绝，余量序列ε平稳。图11（b）为自回归模型、统计模型和CA模型对奇异成分的估计结果，3种模型的复相关系数分别为0.743 2，0.871 5和0.994 5。

图11 CA方法的估计结果Fig.11 Estimation results of the CA method

3 结论

1）为消除奇异成分对大坝变形安全监控结论客观性的影响，运用PCA理论，建立了SPE和CSPE，借助假设检验，提出了PCA辨识准则，在此基础上，基于CA原理，应用ADF检验和逐步回归法，提出了CA似然估计模型。利用陈村拱坝和锦屏一级拱坝径向变形原位监测资料，检验了PCA-CA方法的有效性。

2）拉依达准则、狄克松准则和t准则以1维时间序列为分析对象，辨识性能对样本分布型式的依赖性较大，仅体现了概率意义。PCA准则针对多维数据序列进行分析，不仅包含概率含义，而且考虑了多测点变形的主成分关系，辨识性能最佳。

3）自回归模型和统计模型着重分析1维时间序列，其中：自回归模型仅考察了前期监测数据的时间波动规律，外延性较差；统计模型刻画了水压、温变和时效因素，外延性优于自回归模型，但属于半经验模型，估计精度仍不足；CA模型以多维数据序列为分析对象，既刻画了变形随时间的波动特征，亦表征了多测点变形间的协整关系，同时也反映出外部作用的综合效应，外延性较好，取得了最佳的估计精度。

4）PCA-CA方法要求：①t1效应量对原始变形序列X的解释程度e1尽可能大，通过工程实例1可知，当e1=95.23%时，PCA准则可有效辨识出奇异数据；②余量序列平稳。对于我国已修筑的部分老坝，布设的变形监测仪器较少，不易满足上述条件，此时，仍需采用常规方法。