基于轴桥柔性的100%低地板车动力学分析*
2022-11-04戚壮张成成王美琪刘鹏飞
戚壮,张成成,王美琪,刘鹏飞
(1.石家庄铁道大学机械工程学院 石家庄,050043)
(2.中车唐山机车车辆有限公司动车检修事业部 唐山,063000)
引言
随着大中型城市人口数量的快速增加,发展城市轨道交通显得尤为重要。与城市地铁轨道交通相比,城市轻轨交通设备维护费用和系统耗能更低,其中100%低地板车具有以下优点:①地板面低,无需设立高站台,方便乘客上下车;②建设周期短并且节能节地,可与路面交通实现路权共享等。
我国越来越多的大中型城市开始引入低地板车并投入运营,作为公共交通车辆,其乘坐舒适性和运行安全性必然会受到广泛关注。轴桥结构作为车辆的簧下质量,其大小会影响轮轨相互作用,从而影响车辆的动力学性能,如平稳性、安全性等。一般情况下将簧下质量视为刚体进行动力学建模,而在车辆的实际运行中由于簧下质量结构的不同,其固有模态振型会在轮轨激励频率和设备自振频率产生共振时表现出来,从而影响车辆的动力学性能。笔者以某型100%低地板车的簧下轴桥设备为研究对象,运用模态叠加法进行坐标变换,在建立了刚柔耦合模型的基础下,与多刚体模型在轨道不平顺激扰下的振动响应和动力学性能进行对比。对比分析多刚体模型和刚柔耦合模型的动力学性能后,进一步对簧下轴桥柔性特性进行研究,为以后100%低地板车的工程应用研究提供一定程度的借鉴。
1 刚柔耦合模型动力学建模
1.1 轴桥有限元模型的建立及模态分析
此型100%低地板车采用独立旋转车轮[1],轴桥是连接轮对的重要结构件,且作为簧下质量,其结构形式和本身特性不仅对车辆的轮轨相互作用影响巨大,而且对整车车辆动力学性能也有重要影响,因此将其考虑为柔性体,并研究其弹性特性对整车动力学的影响是很有必要的[2]。
基于柔性体轴桥有限元模型,进行自由模态计算,得到轴桥的自由振动模态,根据轴桥的振动模态分析其振动特性,求解出振动方程特征根和振动向量,得到每一阶的固有频率和振型。将轴桥的空间物理坐标转换为模态坐标是求解步骤的关键。在小变形假设的前提下,浮动坐标系方法是将物体的运动视为浮动坐标系的大范围运动与小弹性变形的叠加[3]。
图1为柔性轴桥的空间坐标表示。基点O为附着在此柔性体上的质点,选择浮动坐标系O′xyz。P为柔性体上的任意点,此任意点的运动可分解为浮动坐标系的牵连运动和相对浮动坐标系的变形运动的叠加。并取P点相对惯性参考系Oxyz,其相对于Pt点的矢径为RP,相对于浮动坐标系的矢径为RO,设柔性体在发生变形前的位置为Pt0,ρ和μ分别为P点的弹性形变向量和柔性体未发生形变时P点相对浮动坐标系的位置向量,rop为P点的位移矢量,如图1所示,则有
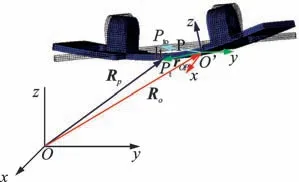
图1 柔性轴桥的坐标表示Fig.1 The coordinate representation of the flexible axle bridge

为计算P点加速度,将式(1)对t进行2阶求导,得到

其中:ω为浮动坐标系O′xyz的转动角速度。
以描述浮动坐标系O′xyz相对惯性坐标系姿态的角坐标θ=(θ1θ2θ3)的导数来表示浮动坐标系的角速度ω

则浮动坐标系的广义坐标可以表示为

如果改用欧拉参数代替绝对坐标描述浮动坐标系的姿态,则q中的θ应以欧拉参数的坐标阵Λ代替。
变形位移μ用模态分析综合法离散为有限自由度,则可表示为

其中:Φ为形函数矩阵,即模态分析法中的模态函数矩阵;qd为nd个模态坐标组成的阵列。如若不考虑柔性体内部阻尼的影响,则此时柔性体的自由振动微分方程是
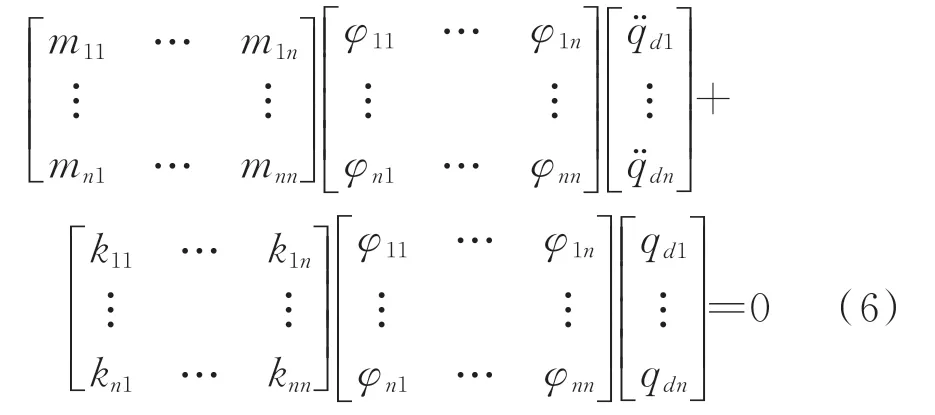

其中:M矩阵为柔性体的质量矩阵;K矩阵为柔性体的刚度矩阵。
将两个矩阵转换为对角矩阵便于对微分方程解耦,即

其中:

式(6)变为
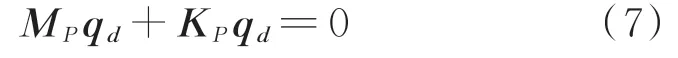
此时质量矩阵和刚度矩阵都是正定矩阵,正定系统只可能出现形如q=φasin(ωt+φ)的同步运动,即将q=φasin(ωt+φ)代入式(7)中,得下列齐次方程组
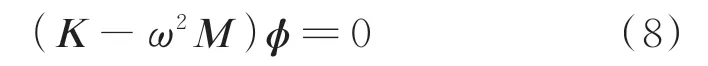
式(8)有非零解φ的充分必要条件是系数行列式为0,即

由式(9)可求解方程对应的n个特征值ω1,ω2,…,ωn,从而可求解φ1,φ2,···,φn,得到

即得到振动微分方程,该过程将求解空间耦合向量μ转化为了求解模态向量矩阵φ,进而求解系统固有频率得到计算结果。
轴桥的固有频率在第3阶达到了152.53 Hz,传统车辆的振动频率主要集中在低频,显然高频在本研究中并无研究必要。通过有限元法求得其前20阶自由模态,一般截断模态取分析模态的2倍,以保证求解精度,因此笔者取其前10阶模态进行研究,其振动频率见表1。由表可知,此柔性轴桥的振动形式主要体现为垂向弯曲和扭转,因此后续重点分析其出现的振动响应结果。部分自由模态振型如图2所示。

表1 柔性轴桥前10阶自由模态Tab.1 The first 10 free modes of the flexible axle

图2 部分自由模态振型Fig.2 Partial free vibration modes
1.2 刚柔耦合动力学建模
独立旋转车轮低地板车辆的转向架结构主要包括轮对、轴桥、构架以及一、二系悬挂装置,笔者主要研究簧下质量轴桥的柔性特性,轴桥材料为某种合金钢,其弹性模量为210 GPa,泊松比为0.3,密度为7 900 kg/m3[4-6]。在HYPERMESH中 实 现 柔 性 体的离散,在ANSYS中求解模态,进一步在UM动力学软件中搭建了100%低地板车整车刚柔耦合动力学模型。图3为UM动力学软件中的100%低地板车整车动力学模型,图4为转向架刚柔耦合动力学模型的建模过程。

图3 整车动力学模型Fig.3 Vehicle dynamics model
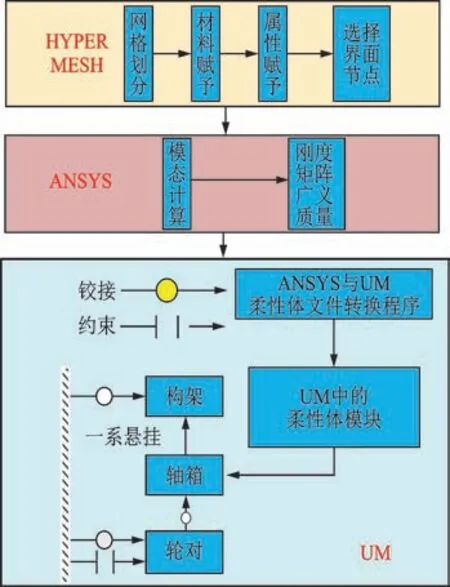
图4 转向架刚柔耦合模型建模过程Fig.4 Rigid-flexible coupling model modeling process of bogie
2 刚柔耦合模型动力学对比分析
2.1 轴桥的振动响应对比分析
车辆在运行过程中会受到轨道随机不平顺的激扰,该激扰由轨道层级传递到车体引起整车振动,根据城市有轨电车的运行情况,以美国Ⅴ级谱作为轨道随机不平顺激扰,车轮踏面为某种特殊车轮踏面。在速度为70 km/h的工况下对振动响应明显的一系弹簧座处进行观察研究,并进行轴桥柔性模型和刚性模型的振动响应特征对比分析[7-8]。
图5分别为轴桥刚性模型和轴桥柔性模型一系弹簧座处的横向振动和垂向振动加速度时域响应分析图。由图可知:横向振动加速度除个别刚性冲击外,柔性体整体的振动响应要低于刚性体,并且振动规律也完全不同;而在垂向加速度振动响应的比较中,两者无论从振动规律还是振动加速度幅值大小都几乎相同。
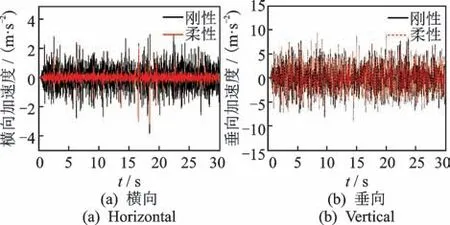
图5 加速度对轨道不平顺的时域响应Fig.5 Time domain response of acceleration to track irregularities
图6分别为轴桥刚性模型和轴桥柔性模型在弹簧座处的横向振动和垂向振动加速度频域响应分析图。由图可知:刚性模型横向加速度的振动能量主要集中在5~28 Hz,而刚柔耦合模型则是集中在1~30 Hz,且幅值相较于刚性模型振动低15%左右;而垂向振动的频域分析中,除刚柔耦合模型能量幅值在2~10 Hz略小于刚性模型外,两模型的整体振动响应规律和能量分布大致相同。由计算结果发现轴桥的垂向弹性特性并未表现出来,推测在此工况下轴桥的垂向弹性特性并未被激发。
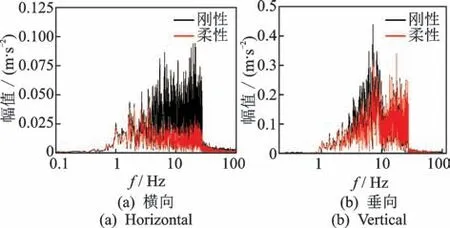
图6 加速度对轨道不平顺的频域响应Fig.6 The frequency domain response of acceleration to track irregularities
2.2 整车安全性对比分析
笔者研究的轴桥作为簧下质量,会直接对轮轨关系造成影响,当车辆通过轨道线路不平顺时,会产生较大的轮轨动作用力,此作用力会影响列车安全性、平稳性和稳定性等,因此需要在考虑此轴桥结构本身的弹性特性下,基于整车动力学模型对安全性进行分析。
设置车辆通过线路的圆曲线长度为150 m,缓和曲线长度为100 m,曲线半径为300 m,曲线超高为0 mm,笔者此处未设超高旨在极限情况下考虑车辆的曲线通过性,至于不同工况下的曲线通过性分析会在后续研究中展开[9-10]。以美国V级谱为轨道随机不平顺激扰,分别让刚性模型和刚柔耦合模型以不同的车速通过曲线,计算轮轴横向力、轮轨垂向力、脱轨系数和轮重减载率,并进行对比分析。
图7为安全性计算结果。由计算结果可知:刚柔耦合模型的轮轴横向力、脱轨系数指标都高于刚性模型,尤其脱轨系数平均升高20%左右,这可能是因为轴桥的横向弹性特性被激发造成轮轨作用剧烈,而导致动力学性能下降;轮轨垂向力、轮重减载率系数则是降低的,这可能是因为轴桥的垂向弹性特性并未被激发,但在刚柔耦合动力学模型中考虑了轴桥的柔性,其自身的弹性适当的缓冲了垂向振动,从而使车辆的动力学性能在垂向上表现出更好的结果。在动力学分析计算时应适当考虑结构本身弹性特性,当其自身弹性对车辆动力学影响较大时,应将结构考虑为柔性体进行刚柔耦合动力学建模。

图7 安全性计算结果Fig.7 The results of security calculation
3 轴桥柔性体的弹性特性分析
通过分析对比柔性轴桥和刚性轴桥时域和频域的振动响应,发现在将轴桥考虑成柔性体时,横向弹性特性被激发,在垂向振动响应中,柔性体和刚性体并未表现出明显区别,怀疑是结构的固有振动频率太高,无法被现有的激励所激发[11-12]。为找出其可被激发的振动频率,通过研究发现适当调整轴桥的厚度可激发其振动模态。阶梯降低轴桥厚度分别建立刚柔耦合动力学模型并进行计算,厚度分别设为50,40,30,20,15和10 mm。轴桥不同厚度下各阶约束模态频率如表2所示。

表2 各厚度轴桥约束模态频率Tab.2Constrained modal frequencies for axlebridge of various thickness Hz
由轴桥的振动模态分析可知,轴桥主要振动模态更多的表现为垂向弯曲和扭转,而在2.1节中的振动响应分析中发现轴桥的横向振动特性已经被激发且对比明显,但垂向振动完全未表现出来,因此本节只研究垂向振动。考虑是轴桥结构原因,将不同厚度下柔性体与原厚度柔性体一系弹簧座处的振动响应进行分析对比,并将计算结果进行傅里叶变换,得到频域的振动响应进行分析。设置2.2节中的计算条件,进行仿真计算。
图8和图9分别为柔性轴桥的厚度为40和30 mm时的垂向振动时域和频域分析图。从图中对比分析可知,将轴桥厚度降低至40和30 mm时与原厚度相比,其时域振动响应与原厚度相比并无明显差异,振动加速度大小几乎一致,振动规律基本相似;在频域振动响应中,其振动能量都集中在1~20 Hz,幅值大小基本一致,振动规律接近一致,表明轴桥的弹性特性仍未被激发。

图8 40 mm厚度柔性体时域和频域的垂向加速度响应Fig.8 Vertical acceleration response of the 40 mm thick flexible body in time and frequency domains

图9 30 mm厚度柔性体时域和频域的垂向加速度响应Fig.9 Vertical acceleration response of the 30 mm thick flexible body in time and frequency domains
图10为轴桥柔性体厚度为20 mm时其垂向振动加速度的时域和频域分析图。由图可知,当厚度降低至20 mm时,在时域响应分析中,轴桥一系弹簧座处的振动加速度相较于原厚度,其幅值有所降低,振动规律也表现出一定的差异;在频域响应分析中,与原厚度轴桥对比发现,此时轴桥振动能量主要集中在1~10 Hz,且两厚度模型的能量峰值也有所不同,20 mm厚度模型能量峰值集中在5 Hz左右,原厚度模型的能量峰值则集中在16 Hz附近,20 mm厚度模型在15 Hz左右其第1阶模态被激发,振动能量达到了此阶段的最大值。此现象与表2中计算结果15.4 Hz相吻合。

图10 20 mm厚度柔性体时域和频域的垂向加速度响应Fig.10 Vertical acceleration response of the 20 mm thick flexible body in time and frequency domains
图11和图12分别为厚度为15和10 mm时轴桥柔性体的时域和频域振动响应。由图可知,在时域响应分析中,15 mm厚度的轴桥振动加速度幅值相较于20 mm时有一定程度的降低,振动规律也有所不同;而在频域分析中,与表2对应的第1和第2阶模态分别在10和15 Hz左右被激发。当厚度为10 mm时,时域响应分析中的振动加速度幅值相较于15 mm明显降低,振动规律也表现出较大差异;在频域响应分析中,其前6阶模态都已被激发,且在其振动模态被激发的频率处发生能量集中。
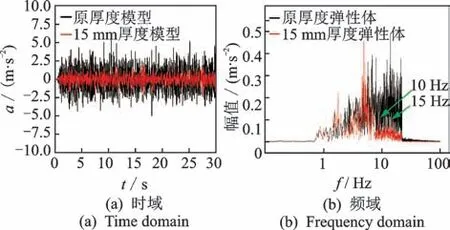
图11 15 mm厚度柔性体时域和频域的垂向加速度响应Fig.11 Vertical acceleration response of the 15 mm thick flexible body in time and frequency domains

图12 10 mm厚度柔性体时域和频域的垂向加速度响应Fig.12 Vertical acceleration response of the 10 mm thick flexible body in time and frequency domains
由上述计算结果可知,轴桥在原厚度50 mm时其结构垂向振动弹性特性并未被激发,随着结构厚度降低,轴桥的固有频率发生改变,弹性特性逐渐被激发。当结构固有频率降至15~25 Hz,其弹性特性开始被激发,当结构固有频率继续降低时其低阶弹性特性将完全被激发。这也解释了2.1中弹性体和刚性体在轨道不平顺激扰下,为何无明显差异。因此,在结构设计时,轴桥的固有频率应高于25 Hz,避免与其他部件发生共振,加剧轮轨相互作用而导致的车辆动力学性能下降。
4 簧下轴桥结构轻量化优化设计
4.1 优化重建模
轴桥结构为簧下质量,而簧下质量的大小对轮轨相互作用关系有着很大的影响,因此对轴桥进行结构轻量化设计会减小轮轨相互作用,减轻轮轨磨损,降低轮轨力,提高车辆的动力学性能。通过拓扑优化的方法得到满足性能要求的结构分布的最优解。轴桥材料为某种合金钢,其弹性模量为210 GPa,泊松比为0.3,密度为7 900 kg/m3,轴桥的初始长度为2.2 m,宽度为0.8 m,厚度为50 mm。
通过HYPERWORKS中的Optistruct拓扑优化模块,设置好优化条件以及约束工况后,将模型提交到Optistruct中进行优化求解,在15次迭代后得到模型的单元密度分布云图,高密度区表示此区域需要材料,低密度区表示此区域无需或需要较少材料。图13为拓扑优化结果。

图13 拓扑优化结果Fig.13 The results of topology optimization
根据密度分布,将图14红色部分的单元变为壳单元,中间连接桥的位置几乎不受力,但是为了其他结构的设计和连接起到轴桥过度的作用,将中间桥的单元适当减少但不完全去掉。优化后结果的网格划分如图14所示,其中实体网格为20 200个,壳单元网格为1 992个。优化后的质量为530.9 kg,较优化前的质量624 kg减少了15%。表3为模型优化前后的固有频率对比。由表可见,优化后轴桥的第1阶频率提高了12.3%,第2阶频率提高了2%。在轨道系统中,车辆运行时振动能量主要集中在低频,约束模态频率提高,更容易避免产生共振,减轻轮轨振动,降低磨损,提高安全性和舒适性。

图14 拓扑优化重建有限元模型Fig.14 The finite element model after topology optimization
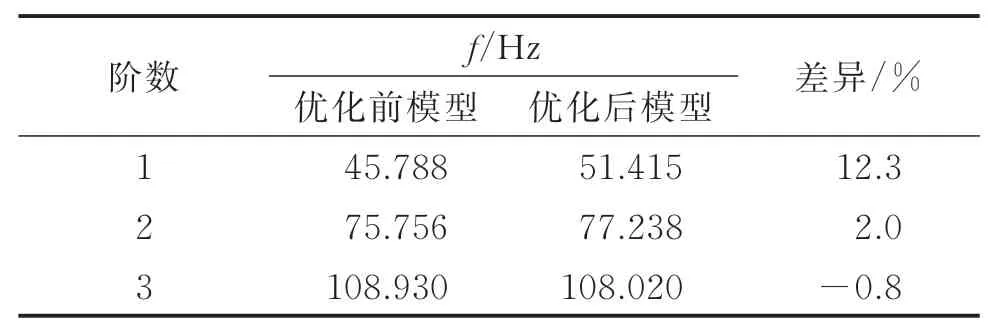
表3 优化频率对比Tab.3 Optimized frequency comparision
4.2 轴桥静强度分析
在结构优化的基础上进行轴桥极限工况的静强度分析,轴桥材料为某种合金钢,其弹性模量为210 GPa,泊松比为0.3,密度为7 900 kg/m3,屈服强度为600 MPa,疲劳强度为300 MPa。考虑轴桥在极限工况下的静强度,参照EN 13749标准中的工况加载方式将车辆的极限垂向载荷和极限横向载荷加载到轴桥上,工况组合方式为车辆通过直线、曲线和道岔[13-14]。各工况下轴桥优化前后的最大Von Mises应力计算结果如表4所示。
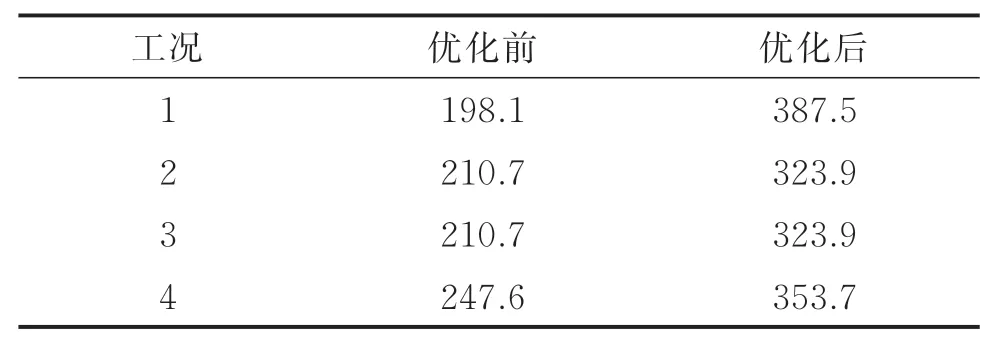
表4 优化前后最大Von Mises应力Tab.4 Maximum stress of Von Mises before and after optimization MPa
图15分别为轴桥结构优化前后应力最大的Von Mises应力云图。由图可知,优化前的最大应力为247.6 MPa,优化后的最大应力为387.5 MPa,均小于材料的屈服极限。优化前后轴桥的静强度满足设计要求。
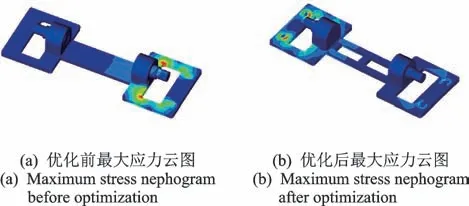
图15 Von Mises应力云图Fig.15 Von Mises stress nephogram
4.3 优化后安全性对比分析
分别以优化前后的轴桥进行刚柔耦合动力学建模,设置2.2中的工况进行安全性计算分析。
图16为优化前后轴桥刚柔耦合模型和刚性模型的安全性计算结果对比。由图可知,在60 km/h条件下,轮轴横向力优化前为11.9 kN,优化后为11.6 kN,降低了2.5%;脱轨系数优化前为0.7,优化后为0.62,降低了11.4%。轮轨横向力和脱轨系数由于簧下质量的降低,减轻了轮轨相互作用力,使车辆安全性提高。轮轨垂向力优化前为43.5 kN,优化后为46.2 kN,升高了6.2%;轮重减载率优化前为0.36,优化后为0.37,升高了2.7%。反观轮轨垂向力和轮重减载率有所升高,可能是由于在轻量化优化后,轴桥本身在垂向上表现出的弹性特性不如优化前,导致轮轨垂向力和轮重减载率升高。
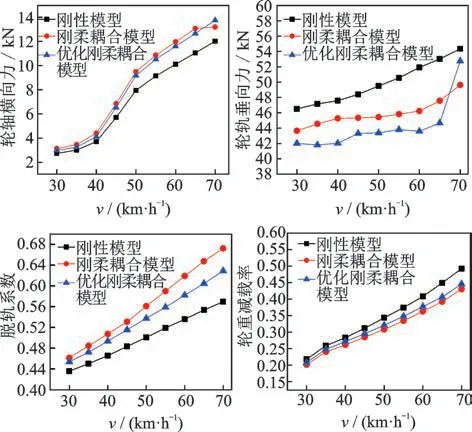
图16 轴桥优化后安全性计算结果Fig.16 Security calculation results of axle bridge after optimization
优化后轴桥的结构改变导致其固有频率也随之改变,而质量的减轻则从根本上减小了轮轴横向力和脱轨系数这两个重要的安全性指标使得车辆动力学性能提升,安全性提高,减少了轮轨磨损,降低检修成本。
5 结论
1)通过模态叠加法,将柔性变形的时间与空间耦合相关性进行坐标变换,达到解耦目的,从而实现了将无限的自由度转换成可以计算的有限自由度。
2)在对比分析多刚体模型和刚柔耦合模型的整车振动响应和动力学性能时,柔性体在整车运行时横向弹性特性被激发,加剧了轮轨相互作用,导致了轮轨横向力增大,脱轨系数升高。而垂向特性未被激发,但在动力学计算时,其本身的弹性适当的缓冲了轮轨垂向力,引起轮重减载率降低。
3)在轨道不平顺激扰下研究基于整车模型的轴桥柔性特性时,与多刚体模型进行对比,发现原有柔性模型的横向弹性振动被激发而垂向弹性特性并未被激发。在轴桥结构的固有频率降至15~25 Hz时,轴桥的垂向弹性特性被激发,且在其固有模态激发时发生能量集中。
4)经过优化的轴桥模型质量减少了15%,1阶频率提高了12.3%,2阶频率提高了2%,且静强度满足设计要求。在安全性分析中,轮轴横向力降低了2.5%,脱轨系数降低了11.4%,结果显示车辆的动力学性能得到提升,达到了优化目的。
