波形腹板钢箱-混凝土组合梁桥的动力特性分析*

2022-11-04冀伟胡世浩齐振峰罗奎张经伟

振动、测试与诊断 2022年5期

冀伟，胡世浩，，齐振峰，罗奎，张经伟

（1.兰州交通大学土木工程学院兰州，730070）

（2.上海市城市建设设计研究总院（集团）有限公司上海，200125）（3.湖南大学土木工程学院长沙，410082）

1 问题的引出

波形腹板钢箱-混凝土组合梁桥是在传统波形钢腹板箱梁桥［1］基础上改进后的新型组合结构梁桥。图1为波形钢腹板预应力混凝土（prestressed concrete，简称PC）组合梁桥构造图。图2为波形腹板钢箱-混凝土组合梁桥的构造图，这类桥梁的优点体现在：①将混凝土底板换成钢底板，大大减轻了桥梁上部结构的自重；②钢底板可以在底板受拉区充分发挥钢材的抗拉性能，避免了混凝土底板易开裂的问题；③采用装配式施工，缩短了施工工期；④造型优美，符合现代桥梁美学特征。

图1 波形钢腹板PC组合箱梁桥构造图Fig.1 Prestressed concrete box girder bridges with corrugated steel webs

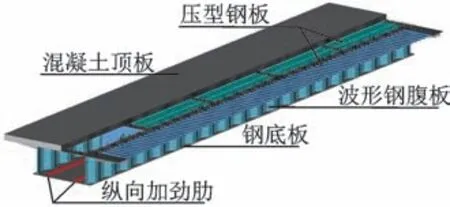
图2 波形腹板钢箱-混凝土组合梁桥构造图Fig.2 Box girder bridges with corrugated steel webs

波形钢腹板组合箱梁桥的力学性能研究在国外起步较早，其静力学方面的研究成果显著。Yi等［2］对影响波形钢腹板失稳和屈曲模式的因素进行了分析，给出了计算合成屈曲强度的公式。Kövesdi等［3］研究了波形钢腹板箱梁弯曲和剪切的相互作用。Papangelis等［4］对斜腹板波形钢腹板箱梁的抗剪承载力进行了研究。Aggarwal等［5］对影响波形钢腹板局部剪切屈服的影响因素进行了分析。国内的学者对波形钢腹板箱梁桥的研究主要集中在静力性能、动力性能及疲劳性能等方面［6］。陈水生等［7-8］研究了波形钢腹板多塔斜拉桥的自振特性以及单箱多室波形钢腹板PC组合箱梁桥的动力特性。郑尚敏等［9］通过模态试验和有限元模拟分析了单箱多室波形钢腹板组合箱梁的动力性能。冀伟等［10-14］在该桥型的自振频率分析、动力冲击系数及挠度计算等方面开展了大量的研究工作。陈凌秀等［15］通过建立有限元模型，对波形钢腹板箱梁桥进行了参数分析。桂水荣等［16］对大跨度波形钢腹板箱梁桥动力特性的影响因素进行了详细的分析。张紫辰等［17-18］研究了波形钢腹板组合箱梁桥的竖向弯曲性能及波形钢腹板的褶皱效应对其力学性能的影响。胡霖远等［19］基于Zig-zag理论对波形钢腹板箱梁桥的自由振动特性进行了分析。

笔者应用ANSYS有限元分析软件，以实际工程为背景，建立有限元分析模型，通过试验数据与有限元模型结果的对比，验证了有限元模型的正确性。随后，以箱间横联的类型、横隔板间距及波形腹板的厚度等为分析对象，研究其对该桥自振频率和振型的影响规律，并拟合出该桥梁的弯曲自振频率计算公式。本研究结论可为波形腹板钢箱-混凝土组合梁桥的设计提供参考。

2 工程背景

笔者依托甘肃省兰州市G1816乌海-玛沁高速景泰至中川机场段公路工程项目，该项目南起机场高速公路（S1）中川收费站管理所，北至Z031路口，是我国首座装配式波形腹板钢箱-混凝土组合梁桥，并于2019年8月10日正式通车。该项目主匝道桥跨布置从南向北依次为1 830 m波形腹板钢箱-混凝土组合简支梁桥+（42 m+4×50 m）连续梁桥+（5×50 m）连续梁桥+（3×30 m）简支梁桥。主匝道桥梁按照双向四车道设计，桥梁全宽为20.0 m（4片主梁），横断面布置为0.5 m边防撞护栏+9 m行车道+1 m中央防撞护栏+9 m行车道+0.5 m边防撞护栏=20.0 m。笔者以30 m波形腹板钢箱-混凝土组合简支梁桥为研究对象，对其进行试验研究与参数分析。图3为主梁横截面尺寸示意图。

图3 桥梁横截面几何尺寸（单位：mm）Fig.3 Cross-sectional dimensions of bridge(unit:mm)

桥梁翼缘位置设置开口型压型钢板，钢箱梁上部设置闭口型压型钢板，主要起到支护模板的作用，进行力学分析时可以不予考虑。图4为2种压型钢板的构造图，钢箱梁采用BCSW1200型波形钢腹板，波长为1 200 mm，波高为200 mm，厚度为10 mm。图5为波形钢腹板尺寸示意图，钢箱梁的混凝土顶板厚为250 mm，钢底板厚度为20 mm。钢底板上设置2道高为180 mm的纵向加劲肋。钢箱梁内部设置横隔板，每片横隔板上设置3道双面竖向加劲肋，横隔板的纵向标准间距为4.8 m。两箱梁之间对应横隔板位置共设置3道箱间横联，两端位置则设置混凝土端横梁。另外桥址区地层较简单，基础持力层承载力高，地质条件好，属抗震有利地段。下部结构桥墩高度均在10 m左右，墩、梁内力均衡性较好。在研究上部结构时，没有考虑桥墩和基础的影响。

图4 压型钢板Fig.4 Profiled steel sheet

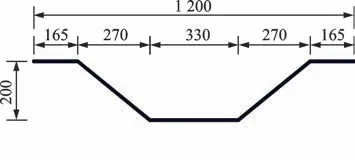
图5 波形钢腹板几何尺寸（单位：mm）Fig.5 Dimensions of corrugated steel web(unit:mm)

材料设计参数如下：混凝土材料为C50，弹性模量Ec=3.45×104MPa，重力密度γc=26.0 kN/m3；钢材的弹性模量Es=2.06×105MPa，重力密度γs=78.5 kN/m3。

3 模态试验

本次的试验对象为主匝道长30 m、宽20 m的波形腹板钢箱-混凝土组合简支梁桥，试验的动力测试采用脉动法，环境激励采用非人工激励的方式，利用拾振器采集得到桥梁结构在地脉动、风载等环境激励下产生的微幅振动信息，进而得到桥梁结构的自振特性。图6为桥梁现场数据采集照片，图7为拾振器的桥面布设图，图8为环境激励下桥梁测点处的加速度时程响应及功率谱密度图，图9为桥梁实测1阶振型。

图6 桥梁动态数据采集Fig.6 Dynamic data acquisition of bridge

图7 桥面测点布置（单位：mm）Fig.7 Layout of measuring points on bridge deck(unit:mm)

图8 加速度时程与功率谱密度图Fig.8 Acceleration time history and power spectral density diagram

图9 实测1阶振型Fig.9 Measured results of 1st order mode shape

综上，波形腹板钢箱-混凝土组合梁桥的第1阶竖向弯曲自振频率实测值为3.762 Hz，为第3.2节有限元模型正确性的验证提供参考依据。

4 有限元模型

4.1 建立有限元模型

采用ANSYS18.2有限元分析软件，建立波形腹板钢箱-混凝土组合简支梁桥的有限元模型，如图10所示。为了更好地模拟桥梁的实际结构构造，所建有限元模型采用壳单元和实体单元2种单元类型。波形腹板钢箱-混凝土组合简支梁桥的顶板、端头板以及两端箱间横梁均为钢筋混凝土结构，采用Solid45来模拟；底板、腹板、横隔板、横隔板上设置的双面竖向加劲肋、纵向加劲肋以及箱间横联均为钢结构，采用Shell63来模拟。波形腹板钢箱-混凝土组合简支梁桥的支座约束为：梁的一端采用滚动铰支座，约束横向（Ux）及竖向（Uy）2个方向上的位移；梁的另一端采用固定铰支座，约束横向（Ux）、竖向（Uy）及纵向（Uz）3个方向上的位移。

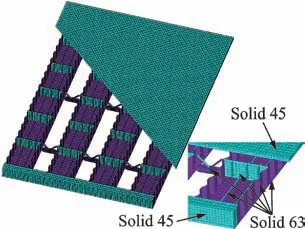
图10 波形腹板钢箱-混凝土组合梁桥的有限元模型Fig.10 Finite element model of steel box concrete composite girder bridge with corrugated webs

在混凝土顶板与波形钢腹板的连接处，即Solid45与Shell63这2种单元类型的变化处，采用刚性连接，用来耦合2种单元的自由度，这样更加符合实际结构的连接效果。图11为有限元模型刚性连接示意图。

图11 波形钢腹板与混凝土顶板的刚性连接Fig.11 Rigid connections between the corrugated steel web and concrete top flange

4.2 验证有限元模型

波形腹板钢箱-混凝土组合梁桥的有限元模型建好以后，为验证模型的精确性，将其自振频率分别与式（1）计算结果及试验数据作对比，结果如下。

《公路桥涵设计通用规范》（JTG D60-2015）给出关于简支梁桥基频f1的估算公式为其中：l为结构的计算跨径；E为结构材料的弹性模量；Ic为结构跨中截面的截面惯矩；mc为结构跨中处的单位长度质量。

将式（1）的计算结果与实测结果进行比较，如表1所示。ω1为规范估算公式计算的基频与实测基频值之间的差值百分比。

表1 规范估算公式计算值与实测值的比较Tab.1 Comparison between the calculated value of the standard formula and measured value

由表1可知，式（1）的计算结果与实测值差值较大，两者计算的基频差值高达8.29%，说明规范给出的估算公式不再适用于计算波形腹板钢箱-混凝土组合梁桥的基频。其主要原因是式（1）没有考虑波形钢腹板的剪切变形效应，而波形钢腹板由于其褶皱效应，抗剪性能较强，因此偏差较大。

将波形腹板钢箱-混凝土组合简支梁桥基频的实测值与ANSYS有限元计算值进行比较，如表2所示。ω2为基频实测值与ANSYS有限元计算值之间的差值百分比。

表2 实测值与有限元计算值的比较Tab.2 Comparison of measured value and finite element calculated value

由表2可知，通过有限元计算的基频值与试验实测值的差值仅为0.76%，两者结果吻合良好，验证了所建立的有限元模型的正确性。

图12为桥梁的前2阶弯曲和扭转振型图，其中ANSYS模型的第1阶弯曲振型图与图9的实测振型图吻合良好。

图12 波形腹板钢箱-混凝土组合梁的弯曲和扭转振动振型Fig.12 Bending and torsional vibration mode shapes of steel box concrete composite girder with corrugated weds

由上述内容可以得出本研究的建模方法合理，所得到的模型精度较高，能较好地还原实际工程中的桥梁结构，可以进行动力性能分析，同时也保证了分析结果的可靠性。

5 结构参数分析

5.1 箱间横联类型对自振频率的影响

为研究箱梁间横联类型对波形腹板钢箱-混凝土组合简支梁桥自振特性的影响规律，建立了K型（实桥）、方钢型及工字钢型3种横联类型的有限元模型。图13为箱间横联有限元模型图，表3为不同横联类型下桥梁前2阶弯曲和扭转振动频率的比较结果。

图13 箱间横联有限元模型Fig.13 Finite element model of transverse connections between box girders

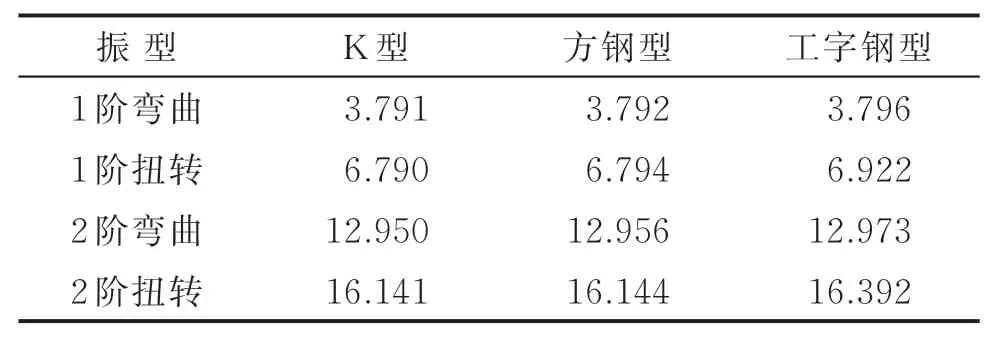
表3 不同横联类型下自振频率的比较Tab.3 Comparison of natural frequencies under different lateral connections Hz

由表3可以看出，K型和方刚型横联对提高桥梁整体刚度的效果相近。工字钢型相比K型横联，1阶和2阶扭转自振频率分别提高1.91%和1.53%。3种类型横联中，工字钢型横联对提高桥梁整体刚度的效果最好，在实际工程中采用此类横联结构，还可以减少钢材的焊接工作量，施工效率较高。

5.2 横隔板间距对自振频率的影响

为研究横隔板间距对波形腹板钢箱-混凝土组合梁桥自振特性的影响规律，依据《公路钢结构桥梁设计规范》（JTG D64-2015）关于钢箱梁横隔板间距的规定，如式（2）所示，建立了横隔板间距分别为5.6，4.7（实桥尺寸），4.0，3.5，3.1和2.8 m等6种有限元模型，对应的横隔板数量依次为4，5（实桥尺寸），6，7，8和9道，桥梁跨径为30 m。表4为不同横隔板间距下桥梁前5阶自振频率的比较结果，图14为单片主梁的前5阶振型图。

图14 单片梁的前5阶振型Fig.14 The first five mode shapes of a single girder

表4 不同横隔板间距下自振频率的比较结果Tab.4 Comparison of natural frequencies under different diaphragm spacings Hz

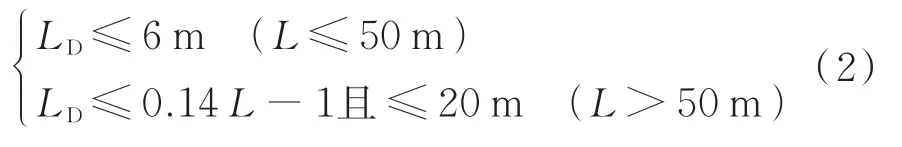
其中：LD为横隔板间距；L为桥梁等效跨径。

由表4可以看出，随着横隔板间距的变化，前5阶自振频率的最大波动分别为0.97%，0.13%，0.75%，0.69%和0.39%，都在1%的范围内。所以在满足规范要求的前提下，设置4道横隔板（横隔板间距为5.6 m）最为合适，即可以适当增加实际桥梁结构中的横隔板间距，节约钢材用量。

5.3 波形腹板厚度对自振频率的影响

为研究波形钢腹板厚度对波形腹板钢箱-混凝土组合梁桥自振特性的影响规律，在假设钢箱梁的混凝土顶板厚度、梁高及底板厚度等设计参数保持不变的前提下，建立了波形钢腹板厚度分别为8，10（实桥），12，14，16，18，20，22，24和26 mm的单片梁有限元模型，桥梁跨径为30 m。图15为桥梁前5阶自振频率随波形钢腹板厚度变化的折线图。

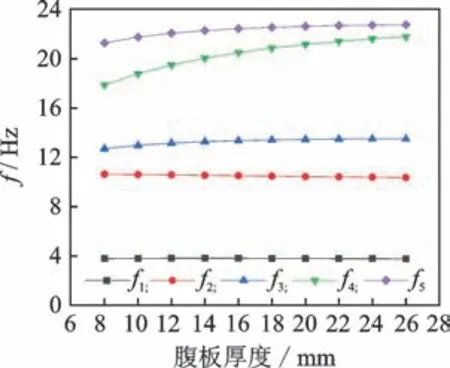
图15 波形钢腹板的厚度对自振频率的影响Fig.15 Effects of thickness of corrugated steel web on natural frequencies

由图15可以看出，波形腹板厚度增加时，1阶扭转自振频率增大21.85%，前3阶竖向弯曲自振频率依次增大0.76%，6.20%和6.90%，1阶横向弯曲振动频率减小2.54%。可见波形钢腹板厚度的变化对扭转振动频率影响较大，对弯曲振动频率的影响较小。桥梁的横向刚度主要由混凝土顶板和钢底板提供，所以f2出现随波形钢腹板厚度增加而减小的情况。

6 公式拟合

经过第4节的结构参数分析，再结合式（1）可知，桥梁的计算跨径和梁高对自振频率的影响较大。通过多项式拟合对式（1）引入修正系数κ，如式（3）所示

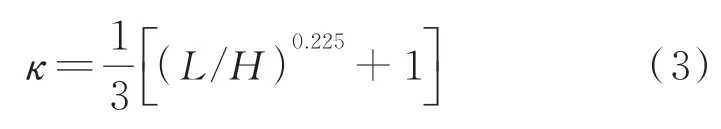
其中：L为桥梁的计算跨径；H为梁高。

将式（3）代入式（1），得到计算波形腹板钢箱-混凝土组合梁桥基频的修正公式

保持波形腹板钢箱-混凝土组合简支梁桥的计算跨径不变，即将计算跨径取为30 m，仅改变梁高，依次将梁高取为1.0，1.2，1.5和2.0 m。利用式（4）和ANSYS有限元计算的波形腹板钢箱-混凝土组合简支梁桥的基频如表5所示。表5中ω3为式（4）计算值与有限元计算值之间的差值百分比。

表5 不同梁高下的基频比较Tab.5 Comparison of fundamental frequencies under different girders heights

保持波形腹板钢箱-混凝土组合简支梁桥的梁高不变，即将梁高取为1.5 m，仅改变简支梁的计算跨径，依次将计算跨径取为20，25，30，35，40，45和50 m。利用式（4）和ANSYS有限元计算的波形腹板钢箱-混凝土组合简支梁桥的基频如表6所示。表6中ω4为式（4）计算值与有限元计算值之间的差值百分比。