滑坡灾害监测的圆弧合成孔径雷达大气相位校正方法

杜年春，王玉明，沈向前，谢 翔

1. 湖南师范大学信息科学与工程学院，湖南 长沙 410081； 2. 中国有色金属长沙勘察设计研究院有限公司，湖南 长沙 410117

受复杂地质条件影响，我国地质灾害频发，造成大量人员伤亡和经济财产损失。自然资源部地质灾害技术指导中心发布的2020年全国地质灾害灾情显示，当年全国共发生地质灾害7840起，共造成139人死亡(失踪)、58人受伤，直接经济损失50.2亿元，其中滑坡占地质灾害总数的61.35%。为此，研究测量边坡形变的设备以实现滑坡预警迫在眉睫。微波干涉测量技术通过相位差分处理，能够实现目标形变值的高精度测量，是边坡形变监测领域中极具前景的创新型技术手段[1-10]。地基差分干涉雷达就是基于此技术的测量设备，它利用微波信号以有源方式工作，可有效穿透云、雨、雾等，不受天气条件和能见度的影响，可实现在恶劣气象条件下对边坡的全天时、全天候不间断连续工作，具有优越的环境适应性；同时，它的图像更新速度快，可达1次/min，有利于完成场景的连续实时监测[11-14]。地基差分干涉雷达主要包括地基实孔径雷达(real aperture radar,RAR)和地基合成孔径雷达(synthetic aperture radar,SAR)两类。典型地基RAR系统有瑞士的GPRI(gamma portable radar instrument)[15]、澳大利亚的SSR(slope stability radar)[16]和南非的MSR(movement and surveying radar)[17]。地基SAR可获得较高的方位分辨率，是当前研究的热点，典型系统有意大利的IBIS(image by interferometric survey)[18]、韩国国立江原大学开发的ArcSAR(arc-scanning SAR)[19]、中国科学院电子学研究所的Arc FMCW-SAR[20]及北京理工大学研发的MIMO-SAR[21]等。

ArcSAR是一种特殊合成孔径方式的地基SAR，其应用于形变测量的优势主要体现在：①雷达作用距离远，监测范围广，可获得监测区域内边坡表面的空间连续形变信息，有效监测点数可达数万点，以供分析滑坡体的整体形变情况；②雷达电磁波的波长远大于光波，因此对于地面草丛、灌木等植被具有一定的穿透能力和相位平滑能力，同时对在有风条件下植被摆动更不敏感，对地表覆植被情况的适应性较好；③雷达采用非接触式方式工作，可以直接测量形变，无须在边坡，特别是高位边坡、松软边坡表面安装任何附属设备，确保人员和设备的安全；④雷达能实现方位向360°高分辨率扫描，具有部署灵活的特点，在复杂山区环境下可实现大范围和多区域的监测，尤其是在“两山夹一沟”区域、大范围接续矿坑等场景有较大的应用需求；⑤雷达在全方位扫描时，其方位向分辨率可保持不变，这为后续信息处理流程的一致性及快速算法的设计提供了有力支撑。

ArcSAR形变测量误差由相位差误差引起，而相位差误差则由噪声和大气相位引起。其中噪声引起的误差与时间无关，不会在长时间持续监测中引起形变误差的累积；而大气相位因不均匀媒质对微波传播路径和方向影响产生，由其引起误差则是时间的函数，会在长时间持续监测中引起形变误差的累积，造成形变值的较大偏离，进而影响滑坡预警，故需对大气相位引起的形变测量误差进行校正。

目前，针对利用微波干涉测量技术的各种形变监测设备，国内外已经开展了一些大气相位校正的研究[22-32]。主要分为两类：一是基于气象数据等的间接校正算法；二是基于监测点相位差的直接校正算法。文献[22]使用自制角反射器作为监测目标，利用温度、气压和湿度等气象数据，根据大气折射模型估算出大气折射率的变化，进而校正大气扰动引起的相位误差，对小范围内目标点大气相位校正获得较好效果。文献[23]通过气象数据集对大气相位扰动进行统计评估，并基于此研究了基于气象参数的大气相位补偿方法。文献[24]将永久散射(permanent scattering,PS)点应用于大气相位校正，取得了较好校正结果。文献[25]基于IBIS-L系统平台，利用地面控制点对大气进行校正的方法进行分析，提出基于稳定点的大气校正方法和不同改正模型，获得较好的效果。文献[26—28]提出一种改进的地基干涉SAR图像非线性大气相位补偿方法，通过对PS点进行子区域划分，反距离加权插值估计出所有PS点的大气相位，解决了常规方法中多参数模型无法准确模拟大气相位，从而无法对部分干涉相位图进行有效校正的问题。文献[29]利用强PS点作为形变相位为零的控制点，进行双向曲线拟合，进而得到较为完整的大气相位。文献[30]提出一种基于迭代的大气补偿方案，以补偿空间三维非均匀折射率分布引起的大气相位波动，而无须任何移动位置的先验知识。文献[31]根据雷达看到的三维地形结构的高度和范围，对观测到的相位进行建模，提出了一种两阶段半经验算法来补偿空域中大气相位。

间接校正算法由于获取数据的空间密度小，使用较少。直接校正算法主要基于PS点进行处理，应用较为广泛，但也还存在着一些问题：一是选择PS点时用到的幅度离差、相位离差等指标的阈值是人为设定的，这使得其对环境的适应性还有待提高，同时这些PS点的选择是一次性，缺乏在线更新机制，难以去掉奇异点；二是使用标靶做PS点用于校正时，需提前布置，工作量大，而使用自动提取的PS点做控制点的算法，又容易选中滑坡区域PS点，影响大气校正结果；三是当PS点使用率不高时，由于用于大气相位估计的点较少，校正算法可靠性不高，而当PS点使用率较高时，由于采用运算量较大的聚类等算法，校正算法运算速度不高；四是在校正过程中，大气相位模型主要采用一维的斜距模型，而二维模型中方位也只采用线性模型，对大角度场景的情况适用性不够。

本文针对上述问题进行研究，并基于自研的ArcSAR系统，提出一种边坡形变监测雷达的大气校正方法。首先，建立大气相位在方位向和距离向上的模型，解决大视角条件下大气相位扰动随方位变化的问题；然后，给出大气相位校正流程及细节，先通过PS点特征提取及归一化，并利用线性分类器解决PS点自动筛选以及稳定PS点自动筛选的问题，再利用PS点及稳定PS点实现两阶段的大气相位校正消除滑坡形变对大气相位估计的影响，提高形变测量的准确性，再通过网格划分，提高大气相位估计速度，解决算法实时实现的问题；最后，进行实测数据处理，通过对比分析大气相位校正前后PS点相位变化历程和形变测量值，验证本文方法的有效性。

1 大气相位模型

监测点的形变值根据其在两幅复图像中的相位差进行计算，设形变值为ΔR,则

ΔR=Δφλ/4π

(1)

式中，λ为微波信号波长；Δφ为相位差。设监测点在图像值分别为A1ejφ1、A2ejφ2,则Δφ可由式(2)计算[33]

Δφ=angle(A2ejφ2×(A1ejφ1)*)

(2)

式中，angle(·)表示计算相角；*表示复共轭。值得注意的是，Δφ实际值可能超出[-π,π],需要进行相位解缠，考虑到其不影响本文算法研究，这里不讨论。

由于大气相位和噪声的影响[33-36]，相位差Δφ可表示为

Δφ=Δφd+Δφa+Δφη

(3)

式中，Δφd为目标形变引起的相位差；Δφa为大气引起的相位差；Δφη为噪声相位差。

Δφa由空气折射率变化Δη(r,θ)引起，模型为

(4)

式中，r为微波传输距离；θ为目标到雷达相对于真北方向的夹角；t为时间。考虑到ArcSAR监测范围可达360°，故Δη是随时间变化与(r,θ)相关的二维函数。根据国际电信联盟最新定义[37]，空气折射率η与气象参数之间的关系可近似表示为

(5)

式中，Pd和e分别代表了干燥大气压力(单位为百帕hPa)和湿大气压力(单位为百帕hPa)；Ta为绝对温度(K)；k1=77.6、k2=72、k3=3.75×105为经验测定系数。可见大气的温度、湿度随时间t在(r,θ)的变化，造成了电磁特性的非均匀，从而使得信号的传播速度和传播方向在穿过整个大气层时不断变化。因此本文直接建立大气相位在距离向和方位向的二元二次函数模型为

(6)

2 大气相位校正算法

图1给出了本文大气校正算法流程，包括两个阶段：一阶段通过PS点筛选和基于网格的大气相位估计，实现全场景快速大气相位校正，分离形变区域和稳定区域；二阶段通过稳定PS点筛选和基于网格的大气相位估计及时域滤波，去除形变PS点的影响及大气相位估计奇异点的影响，实现高性能大气相位校正。

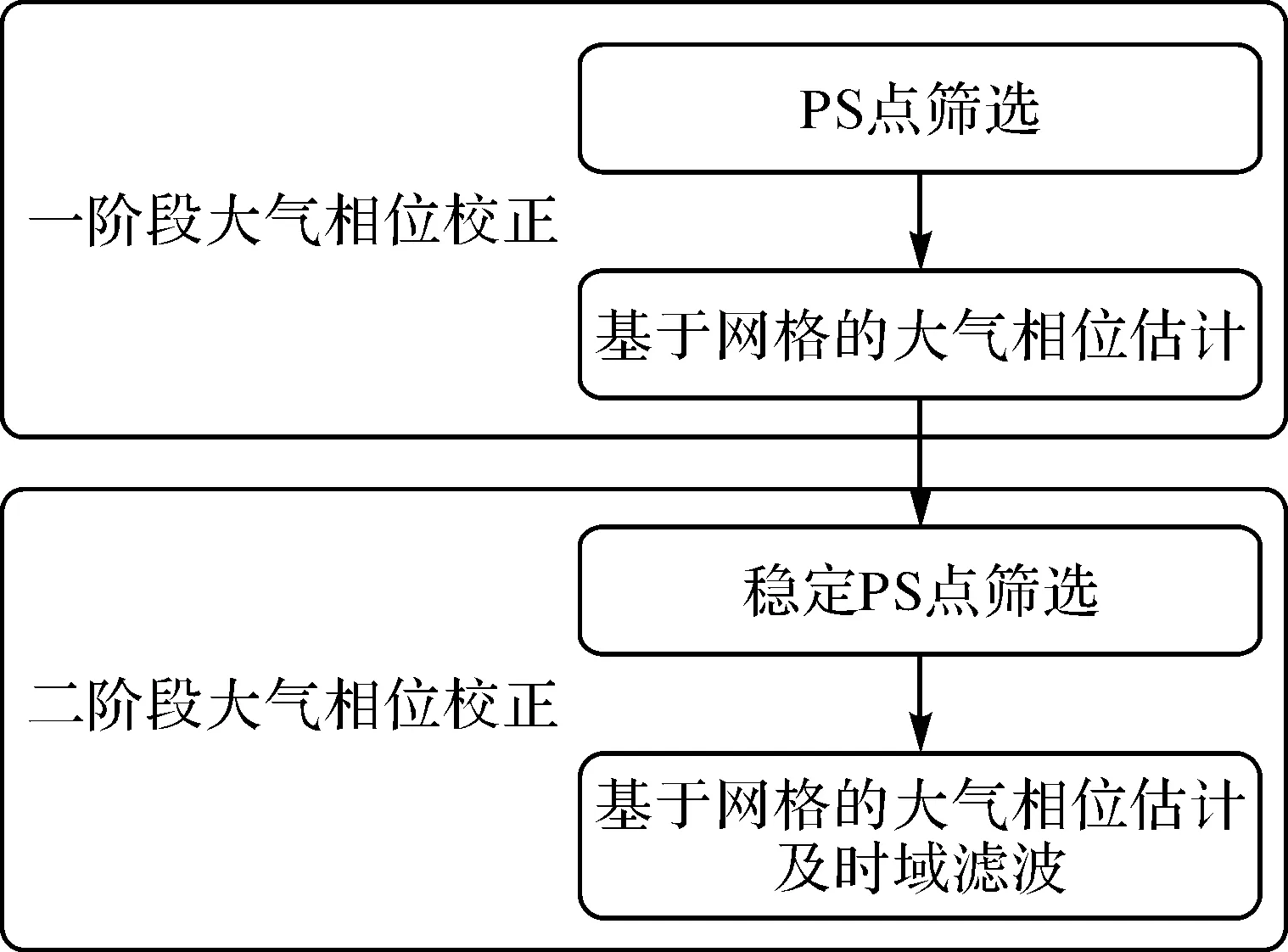
图1 本文大气校正算法流程Fig.1 Flowchart of atmospheric phase correction algorithm in this paper

2.1 PS点筛选

在滑坡预警中，测量边坡区域的形变值，需要设置监测点，故构成其监测点的PS点筛选工作至关重要。为在SAR图像中自动提取PS点，本文采取先特征提取后分类的方法进行PS点筛选。PS点筛选流程如图2所示，包括序列图像的特征提取及分类两个部分。

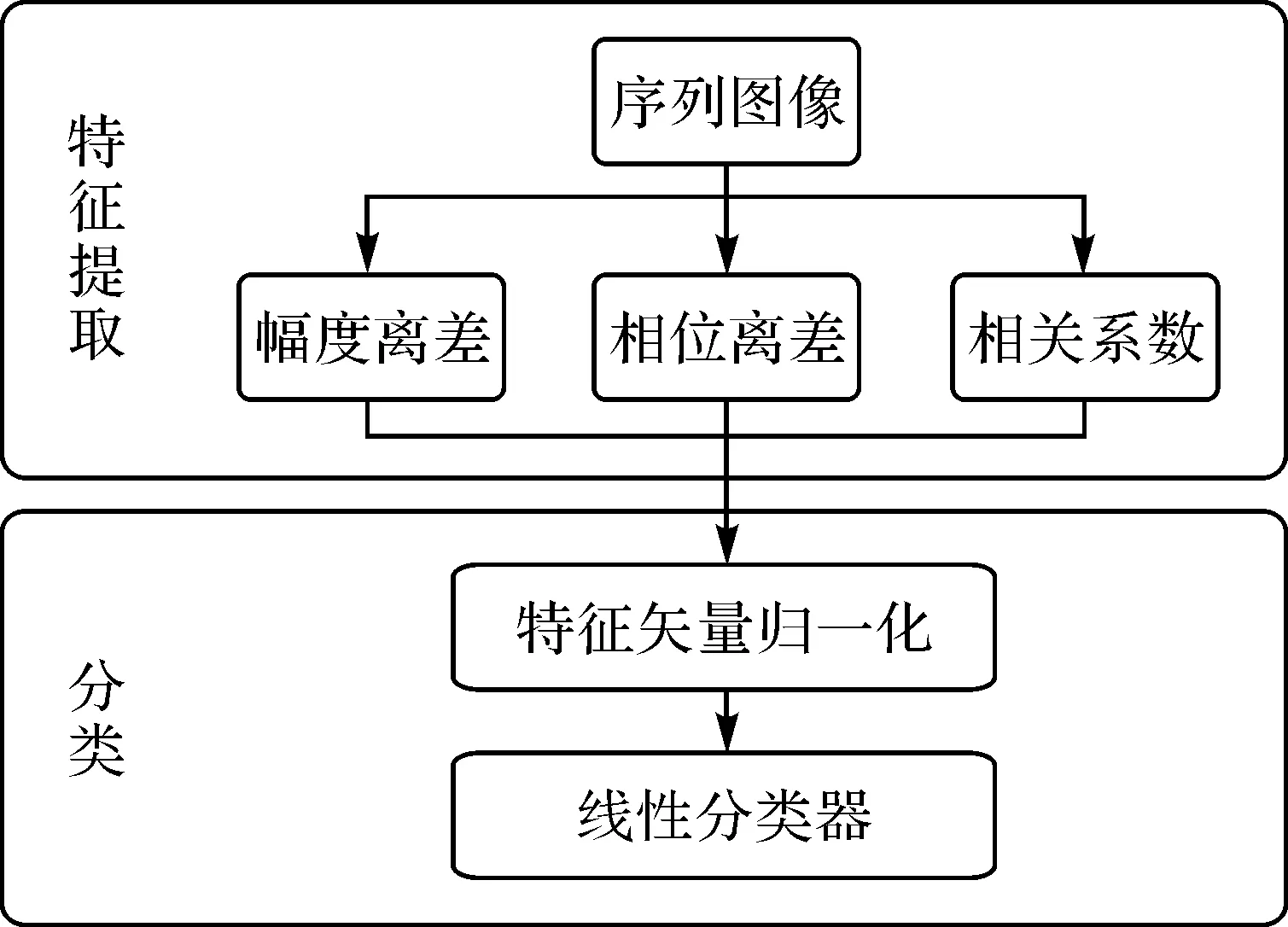
图2 PS点筛选流程Fig.2 The screening process of PS point

设序列图像为Xn,1≤n≤N，其中N为序列图像的数目。xn(i,j)表示图像Xn在像素点(i,j)处的复数值。这里给出主要特征幅度离差、相位离差和相关系数的具体定义。

幅度离差特征Fd首先计算雷达序列图像中每个像元的xn(i,j)的幅度均值m(i,j)和标准差σ(i,j)，Fd表示为

(7)

幅度离差越小，则表示幅度信息越稳定。幅度离差只使用了该像素点的幅度信息，具有计算量小，容易提取的优点。

相位离差特征Fpd首先计算雷达序列图像中每个像元的xn(i,j)的相位pn(i,j)，然后分别计算相位的均值mp(i,j)和标准差σp(i,j)，Fpd表示为

(8)

相位离差越小，则表示相位信息越稳定。相位离差较幅度离差多了相位计算过程，计算量有所增加。

相关系数特征Fc首先需要计算序列图像各像素点的相关系数

cn-1(i,j)=

(9)

式中，I和J为滑动邻域窗口大小；*表示复数共轭。然后对序列cn(i,j)计算每个像元的均值mc(i,j)。则Fc表示为

Fc=1/mc(i,j)

(10)

相关系数越大，则相关系数特征Fc越小，表示相关性越强。相关系数特征涉及像素的邻域，计算量大，但特征稳定，受噪声的干扰较小。

将每个提取到的特征组成矢量，F=[Fd,Fpd,Fc]。考虑到特征矢量各分量的数值不统一，对线性分类器的影响不同，需对其进行归一化。本文根据马氏距离度量原理[38]，通过协方差来解决维度分布不同的问题。协方差矩阵可通过下式得到

C=(F-μF)(F-μF)T

(11)

式中，μF为特征矢量均值。同时由于C是实对称矩阵，可以正交对角化

C=UTΣFU

(12)

式中，U为酉矩阵；ΣF为特征值矩阵。则归一化的特征矢量为Fu为

(13)

由于特征矢量进行了协方差归一化，且每一特征都是单一阈值判决。散射点各特征值越小，其是PS点的概率越大，故分类可选择线性分类器。在分类过程中，首先建立线性分类判决准则

h(Fu)=WTFu+ω0

(14)

式中，WT和ω0为加权系数。在实际数据处理时，可先在场景标定未形变区域，筛选其中的PS点，训练得到加权系数的值。值得注意的是筛选后PS点本身既要有较高的可信度，其数量也能对监测区域有较高的采样。由于雷达工作性能的稳健性和一致性较好，在信噪比满足监测条件时，该分类过程具有拓展性，相应的训练参数可在其他场景中使用。

2.2 基于网格的大气相位估计

为解决聚类等方法引起的运算量大、实时性不高的缺点，本文算法进行网格化大气相位估计。首先将监测区域图像沿方位向和距离向分别等间隔划分网格，方位网格长度为ΔA、距离向网格长度为ΔR。然后分别用最小二乘算法估计每个网格参数β=[β0,β1,β2,β3,β4,β5]。为了兼顾运算速度和大气相位估计的精度，方位网格长度和距离向网格长度常根据实际监测区域的大小和实时处理的时间确定。实时性越高，网格划分越稀疏，反之亦然。监测区域越大，网格划分越稀疏，反之亦然。

大气模型的矩阵化表示为

(15)

式中，e为噪声矩阵，而

(16)

通过筛选的Γ个PS点，用矩阵表示为

(17)

则利用最小二乘算法可得

(18)

进而估计可得

(19)

故可形成一个由网格组成的全场景大气相位，然后根据网格和PS点的位置对应关系，对场景中PS进行第一次大气相位校正。值得注意的是，由于噪声影响，估计得到的部分网格大气相位值可能存在异变，为此，利用大气相位的缓变特性，在全网格空间对其进行空间均值滤波，提高估计相位的稳定性和准确性。

2.3 二次大气相位估计及时域滤波

针对第一阶段筛选的PS点可能存在形变且影响大气相位校正精确度的问题，需要重新选取稳定的PS点进行大气相位估计。由于稳定PS点在零值附近随机变化，而形变PS点通过积累，可出现较大的数值，且形变区域较大，故可采用阈值算法将两者进行分离。具体方法为根据一次大气相位校正的形变结果，选取其60%最接近0的形变值，求取它们的均值md和标准差sd，然后以md+sd为阈值进行分割。

进行二次稳定PS点筛选后，采用与2.2节相同的方法进行大气相位估计、空间滤波。由于空间滤波并不能完全消除大气相位估计时出现的异变值，为保证后续校正的准确性和可靠性，根据大气温度和湿度变化的时间连续性，本文对每一网格估计的大气相位进行卡尔曼滤波，进一步减小大气相位异变值影响。建立状态转移矩阵为

(20)

式中，ωk-1是服从高斯分布的噪声。建立观测方程为

(21)

当形变测量误差优于0.1 mm时，系统波长为12 mm，则v对应的相位误差为3°，其方差为9；而温度引起的噪声为Q=4。且F1=1，F2=1，即可实现大气相位的时域滤波。

由于部分网格存在形变PS点，没有估计大气相位，故采用二维线性插值对这些网格点进行补全，然后实现对全场景PS点进行大气相位校正。

3 试验及分析

本文处理的试验数据源自对云南思茅矿山的监测，时间起始于2020年12月12日。试验区范围为100.523 1°E，22.793 1°N，在位置如图3所示，滑坡主要集中在新开采区域。试验采用的ArcSAR工作频率为24 GHz，带宽500 MHz，转臂长度为1 m，旋转速度(revolutions per minute,rpm)为1转/min，数据更新时间为2 min。试验场景如图4所示。雷达工作在监测边坡底部，做固定处理，顺时针扫描监测。

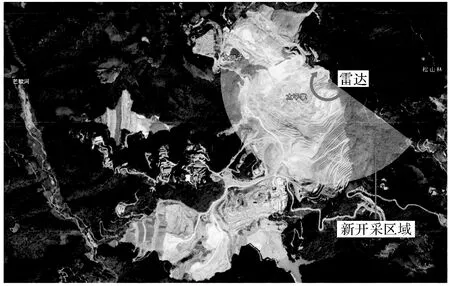
图3 试验场景位置Fig.3 Location of outfield experiment sence

图4 自研ArcSAR系统及试验场景Fig.4 Self-developed ArcSAR and sence of outfield experiment

ArcSAR系统的图像距离向分辨率为0.15 m，方位向分辨率为0.12°，成像范围距离为1 km，方位范围为180°。图5给出全试验场景的直角坐标散射图像，图6给出了试验场景和相应散射图像叠加结果。可以看出，散射图像纹理能够很好地表示监测区域的地貌特征，水平地势散射强度较弱，边坡地势散射强度高，有利于形变监测点提取。

图5 试验场景散射图像Fig.5 Scattering image of outfield scene

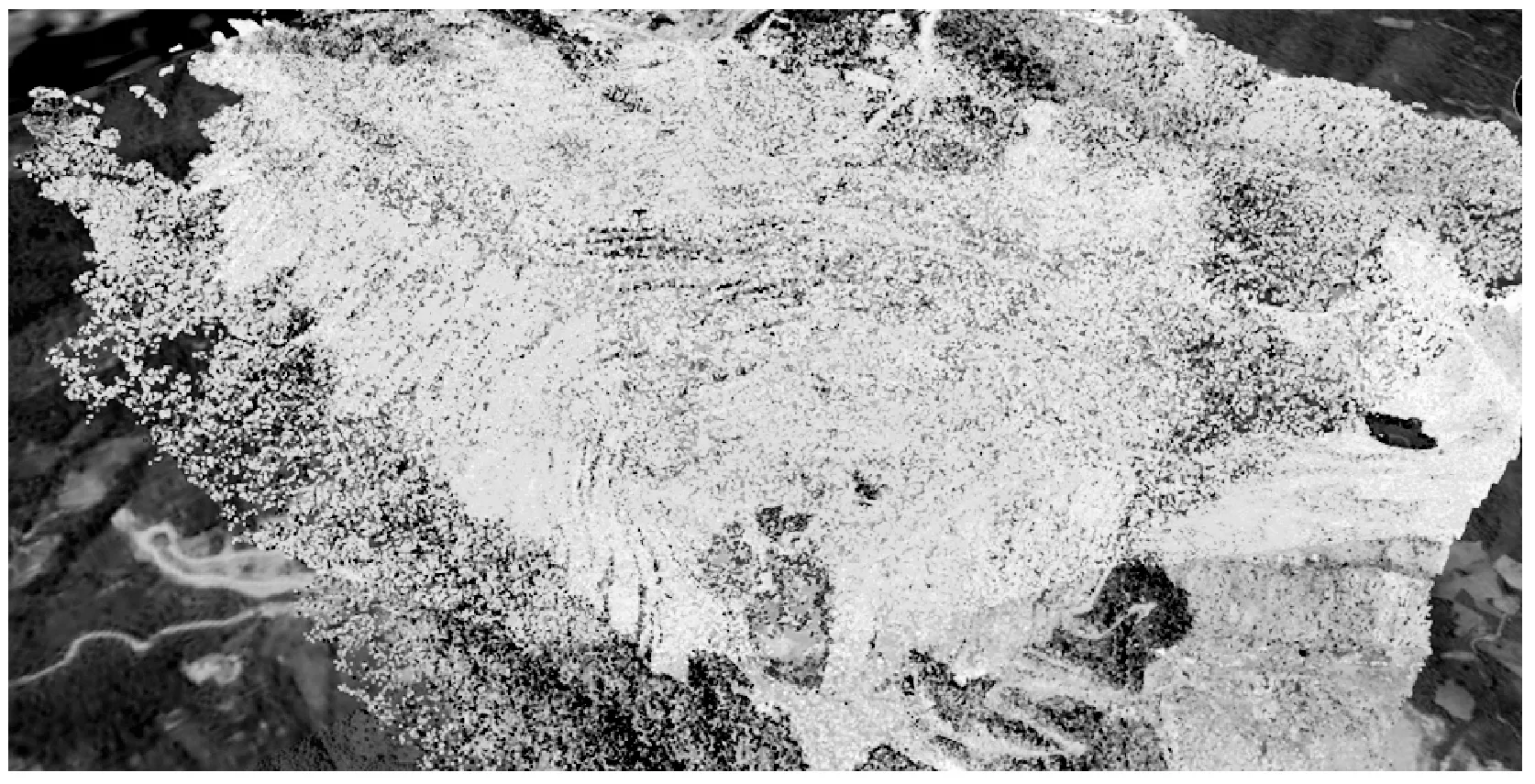
图6 试验场景和散射图像叠加结果Fig.6 Superposition result of outfield scene and scattering image

图7给出了某一时刻PS点特征提取及筛选结果。图7(a)为幅度离差的倒数，由于幅度离差值越小表示PS点越稳定，为便于显示， 这里采用幅度离差的倒数， 可见在3以上的值能表征边坡区域。图7(b)为相位离差的倒数，由于相位离差也是值越小表示PS点越稳定，为便于显示，这里采用相位离差的倒数，可见在3.5以上的值能表征边坡区域。图7(c)为相关系数，由于相关系数值越大表示PS点越稳定，可见在0.6以上的值能表征边坡区域。经过幅度离差、相位离差和相关特征的综合加权分析，试验场景中筛选出PS点的图像如图7(d)所示，用深红色表示。与图5对比可知，筛选得到的PS点数量较多且其位置与重点关注区域吻合，能够充分保证边坡形变的监测。

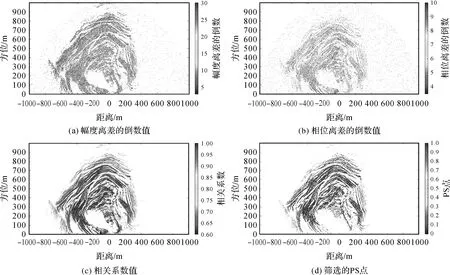
图7 PS点特征提取及筛选结果Fig.7 Feature extraction and screening results of PS points

图8给出了试验场景中稳定PS点和形变PS点的分割结果图像，深红色表示形变PS点，绿色表示稳定PS点。在本文分析的16 h的数据中，图8中形变PS点主要集中在红色椭圆区域。椭圆区域A为实际滑坡区域，椭圆区域B和C则有车辆进行施工作业。可以看出，本文方法估计的形变PS点和稳定PS点与实际情况吻合，具有较高的准确性。值得注意的是，这里筛选的PS点随时间实时更新，后续处理监测区域的形变值也是所有PS点的累积。因此，图8给出的分割图中，多帧累积的PS点较图7中PS点多。

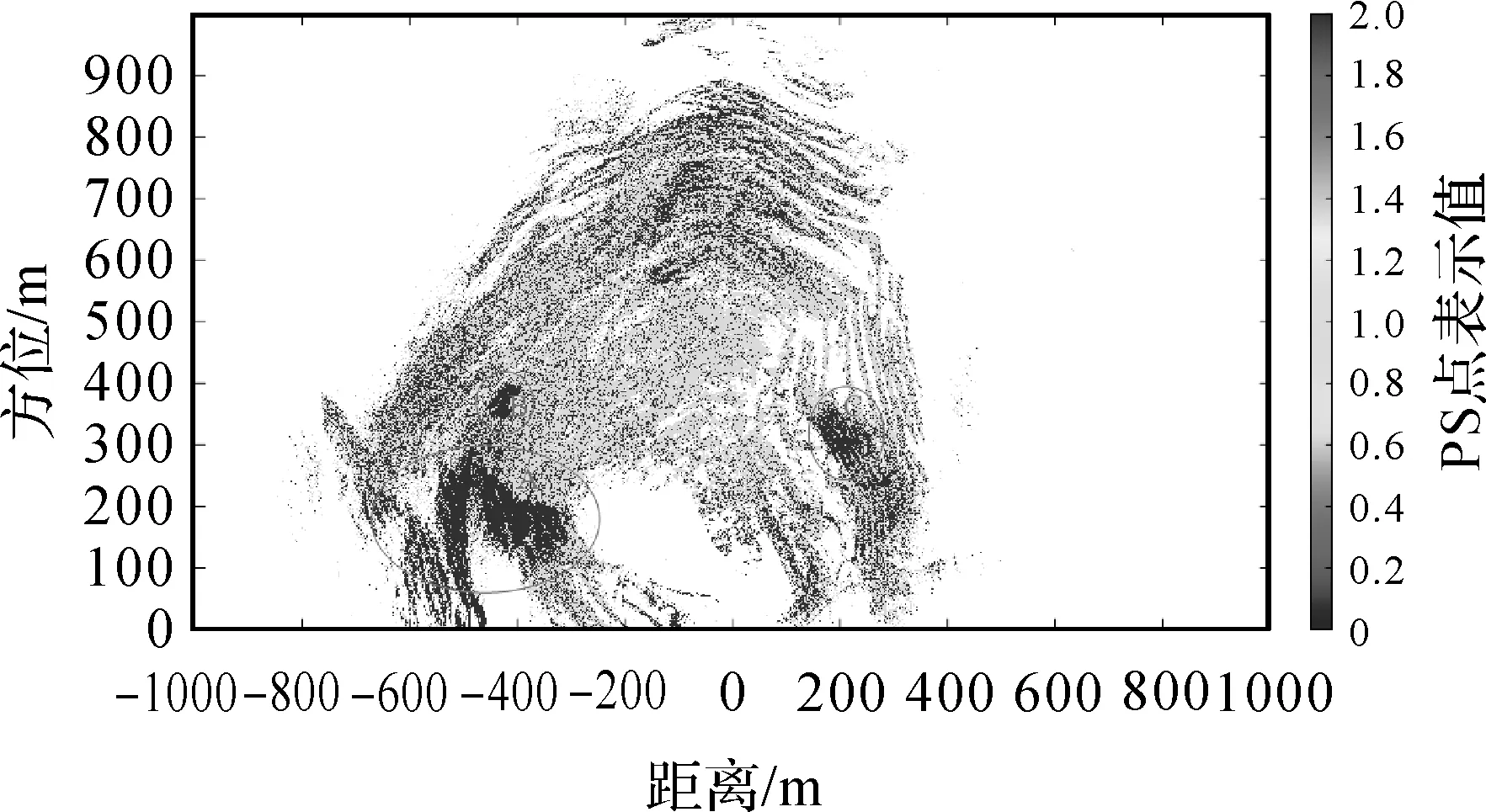
图8 稳定PS点(绿色)和形变PS点(红色)筛选结果Fig.8 The screening result of stable PS points (green) and deformable PS points (red)

图9给出了场景中两个稳定PS点大气相位校正前后的相位变化历程，共16 h。本文分别以距离向30 m，方位向30 m为间隔进行网格划分，然后估计相应的大气相位模型参数。PS点1距离雷达343 m，PS点2距离雷达152.8 m。通过大气相位校正前变化曲线比较可知，距离雷达越远，大气相位扰动影响越大。同时可知，前8 h大气相位扰动影响较小，后8 h大气相位扰动影响变大。通过本文方法处理后，两个稳定PS点的相位均被校正到较小的区间内。可见，本文方法能够有效实现大气相位校正。

图9 两个稳定PS点的相位变化历程Fig.9 The phase change history of two stable PS points

为分析全监测场景大气相位校正效果，图10给出了大气相位校正前后监测区域形变图像，幅度单位为毫米，PS点向靠近雷达方向移动，值为负，表示为蓝色；PS点向远离雷达方向移动，值为正，表示为红色。图10(a)为雷达大气相位校正前的形变值(监测时长8 h)，图10(b)为雷达大气相位校正后的形变值(监测时长8 h)，两者差异不大，与图9所示的情况一致，前8 h大气相位扰动影响不明显，未能引起形变值的大幅度变化。图10(c)为雷达大气相位校正前的形变值(监测时长16 h)，由于大气相位扰动明显加剧，形变值偏差出现累积，稳定区域的形变值也发生较大变化。图10(d)为雷达大气相位校正后的形变值(监测时长16 h)，稳定区域的形变值被校正在合理区间，没有出现较大偏差累积的现象，同时滑坡区域(负值)和施工区域(多为正值)的形变值也被准确反映。

图10 大气相位校正前后监测区域形变值图像Fig.10 Deformation value image of monitoring area before and after atmospheric phase correction

图11给出了2021年9月26日云南思茅矿山监测区域的三维场景与其PS点形变值的叠加。与图8中的椭圆区域A对应，该部分已于2021年4月发生了可见滑坡，其他红色区域和蓝色区域也都与现场施工情况一致，红色多为挖掘区域，而蓝色为填充区域。可以看出，本文方法能够有效实现ArcSAR长时间监测所需的大气相位校正，进而为其准确测量形变奠定基础。

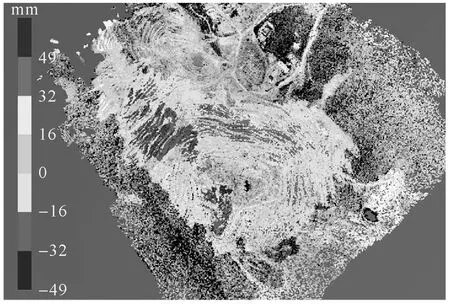
图11 试验场景与PS点形变值叠加结果Fig.11 Superposition result of outfield scene and PS points deformation values

4 结 论

大气相位校正是形变监测雷达长时间监测关注区域稳定性、可靠性的重要保障。本文提出了基于网格划分的两阶段大气相位校正算法。首先通过分类算法，实现PS点的筛选；然后通过划分网格、空间滤波等方法，利用所有PS点估计大气相位，进行第一阶段的大气相位校正；接着通过阈值分割算法，实现了稳定PS点和形变PS点的分离，利用稳定PS点再次估计大气相位，并使用卡尔曼滤波器在时间维度对大气相位滤波，完成第二阶段的大气相位校正；最后实际数据处理表明本文算法的可行性和有效性。本文算法充分利用了网格划分进行大气相位估计的运算速度优势，又通过PS点的筛选、稳定PS点的筛选、大气相位空间滤波、大气相位时间序列滤波等方法保证了校正的准确度。但本文算法也存在着不足，一是时间序列滤波算法较为简单，未引入大气温湿度变及滑坡物理过程的相关信息；二是本文使用的网格尺寸大小由经验给出，计算效率的提高存在不确定性，且网格中PS点密度差异过大也会对大气相位空间滤波造成差异，故需进一步研究自适应网格划分方法。