顾及样本优化选择的多核支持向量机滑坡灾害易发性分析评价

刘纪平，梁恩婕，徐胜华，刘猛猛，王 勇，张福浩，罗 安

1. 中国测绘科学研究院，北京 100036； 2. 辽宁工程技术大学测绘与地理科学学院，辽宁 阜新 123000； 3. 河南省科学院地理研究所，河南 郑州 450052

实施科学有效的滑坡监测预警是防灾减灾工作的重要前提，而智能化、精准化和普适化的先进测绘技术为地质灾害监测预警工作提供了重要保障。目前，以InSAR[1]、地基SAR[2]为代表的遥感技术在滑坡大范围识别和监测中大展身手，以北斗[3]为代表的卫星导航技术正快速推动滑坡高精度实时监测应用的发展。卫星、无人机、测量机器人及地下光纤测量技术等构建的空天地内一体化立体监测网络，能实时获取多层次多尺度滑坡关键监测指标[4]。基于地理空间大数据、机器学习等方法的滑坡易发性分析评价，结合历史滑坡灾情隐患数据可以实现滑坡灾害风险等级的精准反演与快速划分，为地质灾害风险调查和重点隐患排查提供快速有效的依据。

基于地理空间大数据的滑坡易发性分析评价通过构建滑坡灾害点与滑坡影响因素之间的关系，反演区域的滑坡风险等级。滑坡灾害成因复杂，其影响因素主要分为两种：引起滑坡的内部孕灾因子(地形地貌、地质构造、交通水系等)与外部诱发因子(降雨、地震、人类工程活动等)[5]。随着3S技术日益发展，滑坡灾害分析评价模型正逐步从单一模型到组合模型探索研究[6]。单一模型方法可分为统计分析法和机器学习法。统计分析法有证据权法[7]、信息量法[8]、确定系数法[9-11]。常用的机器学习法主要有逻辑回归法[12]、人工神经网络法[13]、随机森林法[14]和支持向量机法[15-17]等。

机器学习分析模型对数据质量有较强的依赖性，数据的质量影响模型预测精度[18]。滑坡易发性分析输入数据包括正负样本数据，一般将滑坡历史清单作为正样本数据，负样本数据包括人工现场选取和数据构建[19]。文献[20—21]提出通过空间距离限制负样本，该方法数据随机性较强，负样本选取质量可靠性低，影响易发性模型训练精度。文献[9]采用下采样法对非地质灾害的栅格单元进行聚类，在聚类中心处选择与灾害点数目一致的非灾害点数据，但该方法受到区域差异的约束。文献[22]结合模糊聚类和支持向量机优化样本选择策略选择非滑坡样本，模型迭代周期长、计算复杂度较高。文献[18]研究发现，SVM由于计算速度快精度高，作为易发性最常用的模型，但是通常采用单一核函数SVM，忽略了多特征之间差异大的问题。文献[23]通过对比不同核函数SVM易发性分析，发现多核RBF函数SVM滑坡易发性精度最高。本文选取9种特征因子构建分类特征，特征之间差异明显，例如年降雨量和坡度表现不同的分布特征，解决了单一核函数SVM模型预测不能表达多特征映射影响预测精度的问题。

针对上述经典的方法没有考虑各孕灾因子各分级状态的滑坡敏感性及单一核函数难以解决多特征映射的差异问题，本文提出顾及样本优化选择的多核支持向量机(multiple kernel support vector machine，MKSVM)滑坡易发性分析评价方法。样本优化选择利用确定性系数法计算各评价因子各分级状态下影响滑坡灾害的敏感性，对敏感值进行加权求和得到各栅格单元的滑坡灾害易发性指数，将滑坡灾害易发性指数的极低和低易发区作为非滑坡点范围约束的同时，结合滑坡点与非滑坡点之间的距离、非滑坡点与非滑坡点之间的距离作为距离约束条件，随机选择与滑坡灾害点数目一致的非滑坡灾害点，可以得到准确性较高的训练负样本数据，该方法通过最大化非滑坡点与滑坡点特征之间差异，并结合一定空间约束，提高负样本选择的合理性；然后在此数据基础上提出MKSVM滑坡灾害易发性分析评价模型，对各特征空间核函数进行线性组合，避免单个核函数映射不合理，提高模型的适用性。

1 研究区概况及数据源

1.1 研究区概况

湘西土家族苗族自治州位于湖南省西北部，坐标为109°10′E—110°22.5′E，27°44.5′N—29°38′N，地处武陵山区与云贵高原过渡带，山间有小型盆地和沿河谷地(图1)。武陵山主脉绵亘中部，呈东北—西南走向，东南部属沅江河谷低山丘陵区，沅江支流武水、酉水为主要河流。全州总面积为15 462 km2[24]。地势由西北向东南倾斜，平均海拨800～1200 m，东西部为低山丘陵区，平均海拔200～500 m，溪河纵横其间，两岸多冲积平原。地貌形态的总体轮廓以山原山地为主，兼有丘陵和小平原，并向西北突出弧形山区地貌。年降雨量1300～1500 mm，雨量集中在春、夏两季。湘西州地质灾害类型以滑坡为主，其次为崩塌、泥石流、地面塌陷等地质灾害，灾害规模均以中小型为主，主要分布于降雨强度大及人类工程活动强烈的区域，其中，暴雨期间仍是地质灾害的高发频发期。

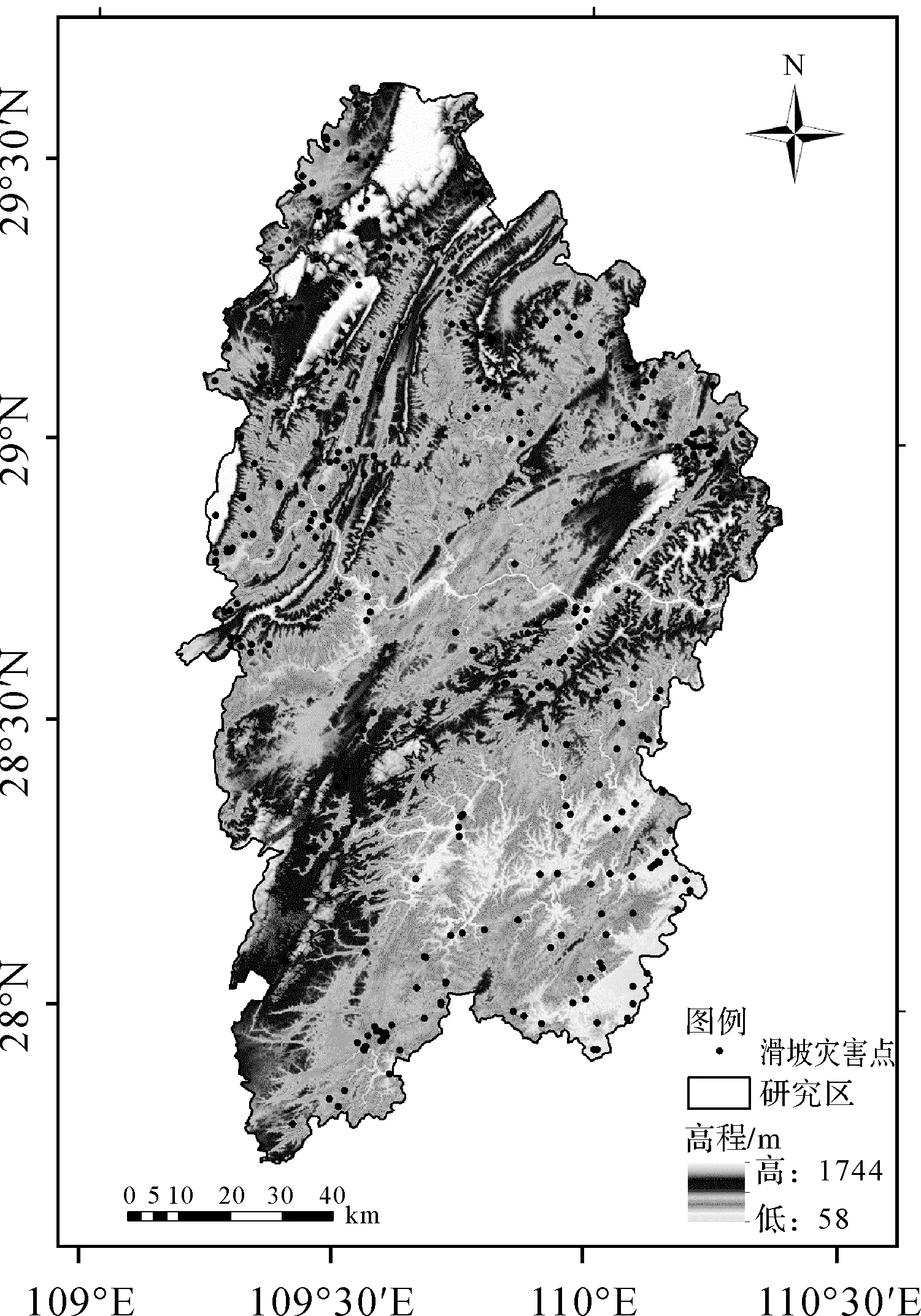
图1 研究区滑坡灾害点分布Fig.1 Distribution of landslide disaster points in the study area

1.2 数据源

湘西州滑坡灾害点来源于中国科学院资源环境科学数据中心资源环境数据云平台(http:∥www.resdc.cn/Default.aspx)，获取时间为2017年，分辨率为30 m。数字高程模型(digital elevation model,DEM)数据来源于美国NASA地球数据网站的ASTER GDEMDEM 30 m分辨率数字高程数据(https:∥search.earthdata.nasa.gov/search)，获取时间为2018年。地质岩性数据来源于中国科学院资源环境科学数据中心资源环境数据云平台(http:∥www.resdc.cn/Default.aspx)，获取时间为2018年，分辨率为30 m。NDVI数据来源于Landsat 8 OLI_TIRS卫星数字产品数据30 m空间分辨率(https:∥search.earthdata.nasa.gov/search)，获取时间为2018年。年降水量数据来源于美国NASA网站的全球降水测量数据level3(https:∥pmm.nasa.gov/precipitation-measurement-missions)，获取时间为2018年。距离道路数据、距离河流数据、距离居民点数据来自于地理国情普查成果数据，获取时间为2018年。为便于统计与分析，结合DEM、遥感影像数据分辨率，将湘西州区按照30×30 m的栅格大小进行划分，划分后的研究区共有31 374 840个栅格单元。

1.3 指标因子选取

根据研究区实际情况以及对影响滑坡灾害发生的地形地貌、地层岩性、地质构造、降雨、地表水及人为因素进行分析[24-29]，选取了高程、坡度、坡向、地层岩性、植被覆盖指数(NDVI)、年累计降雨量、距道路距离、距河流距离及距居民点距离9个评价因子，如图2所示。利用逐步回归法对所选特征因子进行多重共线性检验，通过容忍度(T)和方差膨胀因子(VIF)检验各个特征因子之间的相关性。结果显示，所选特征因子T均大于0.1，且VIF均小于10，说明各个因子共线性程度低，具有较好的独立性。

图2 特征因子Fig.2 Feature factors

2 研究方法

本文提出顾及样本优化选择的MKSVM的滑坡灾害易发性评价方法，通过确定性系数进行样本选择，在训练样本数据集基础上采用MKSVM方法对滑坡灾害易发性模型进行训练与建模，进而实现研究区滑坡灾害易发性评价。技术流程如图3所示。

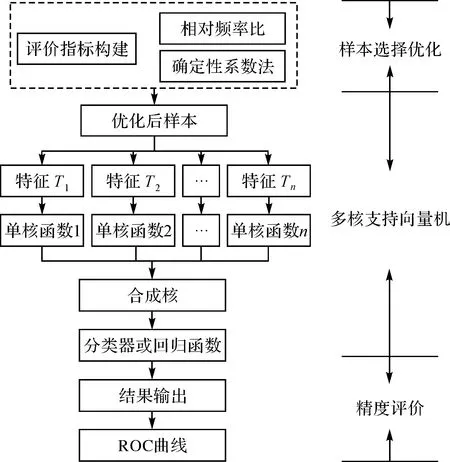
图3 技术流程Fig.3 The technological flowchart

2.1 样本优化选择

样本优化选择首先通过相对频率比综合评价各状态对于滑坡易发性影响的重要程度，实现各评价因子状态的合理划分，然后采用确定性系数法计算各评价因子各状态分级的敏感值和各栅格单元的滑坡灾害易发性指数，在滑坡灾害易发性指数的极低和低易发区随机选择与正样本(即滑坡灾害点数据)数目一致的负样本数据(非滑坡灾害点数据)，二者共同组成滑坡灾害易发性评价训练样本数据集。

2.1.1 相对频率比

相对频率比表示连续型特征因子对滑坡易发性影响的重要程度，其公式如下

(1)

式中，PL为各特征因子各分级状态下滑坡栅格百分比，即为某特征因子条件下各状态分级的含有滑坡灾害点的栅格单元数与整个研究区的滑坡灾害点栅格单元总数之比；PG为各特征因子各分级状态的分级栅格百分比，即为某特征因子条件下各状态分级的栅格单元数与整个研究区的栅格单元总数之比。如果RF为正数，则说明该分级状态下较易发生滑坡灾害；如果RF为负数，则说明该分级状态下不易发生滑坡灾害。

2.1.2 确定性系数法

确定性系数法是一种分析影响事件的各种因素的敏感性的概率函数，在滑坡易发性分析评价中得到广泛的应用[30-32]。CF模型的原理公式如下

(2)

式中，Pc为各特征因子条件下各状态分级的滑坡灾害点发生概率，即为某评价因子条件下各状态分级的含有滑坡灾害点的栅格单元数与栅格单元总数的之比；Pr为整个湘西区内滑坡灾害点发生的概率，即为整个研究区内的灾害点数与栅格单元总数的之比。

在利用CF模型计算出各分级的CF值的基础上进行加权求和，得到各单元滑坡灾害易发性指数，其计算公式如下

(3)

式中，Fj为第j个评价单元的易发性指数；CFi为第i个特征因子各分级的CF值。

2.2 多核支持向量机

支持向量机是一种基于统计学习理论的监督学习方法[33]，核心是构造一个最优超平面，通过最大化样本之间的间隔来区分不同的样本，这经常被用于解决二值分类问题。依据输入数据的特征，SVM通常选取4种核函数[34],见表1。

表1 核函数类型介绍

MKSVM利用多个基本核函数的线性组合来代替传统的单一核函数，能够克服传统单核函数多特征映射不合理的问题[35]。假设有一特征空间{T1,T2,T3,…,Tn}，它们分别从分类问题中最常用的4个核函数(表1)中选取SVM最优核函数。在多核映射的背景下，采用多核线性组合法将各特征空间最优核函数进行线性组合，其公式为

(4)

式中，n为基核函数的个数；Kn为基核函数。常用的核函数有线性核函数、多项式核函数、Sigmoid核函数和高斯核函数，本文采用多个RBF核函数作为基核函数。

MKSVM的优化问题需要同时求解超平面权重和核函数权重。通过两步交替优化的方式求解，首先固定核函数权重求解基本的SVM问题；然后构造关于dm的目标函数，固定超平面权重；最后用梯度下降法求解。

3 试验分析与验证

本文通过CF法进行负样本优化选择得到CF法选择样本，利用文献[18]随机选取负样本得到随机选择样本，分别利用单核SVM模型、MKSVM模型进行试验分析，从易发性结果图、分区结果统计和模型精度验证3个方面，验证本文方法的准确性和可靠性。

3.1 样本构建

在计算各评价因子各状态分级的CF值和各栅格单元的滑坡灾害易发性指数前需完成对各评价因子状态的合理划分。通过等级划分后计算出各特征因子的相对频率比，然后通过确定性系数选取非滑坡灾害点。

3.1.1 特征因子状态分级

对于同一因子的不同状态而言，若对滑坡易发性影响的重要程度相同，则可被划分为同一级别。对于离散型数据，由于本身各个等级就代表了明确的物理意义或不同的用途，因此不必进行等级划分[36]。对于连续型数据，首先将其离散化，对比分析分级栅格百分比、滑坡栅格百分比及相对频率比，综合评价各状态对于滑坡易发性影响的重要程度，对RF值相近的区间进行合并，实现各评价因子状态的合理划分[37-38]，分级结果见图4。

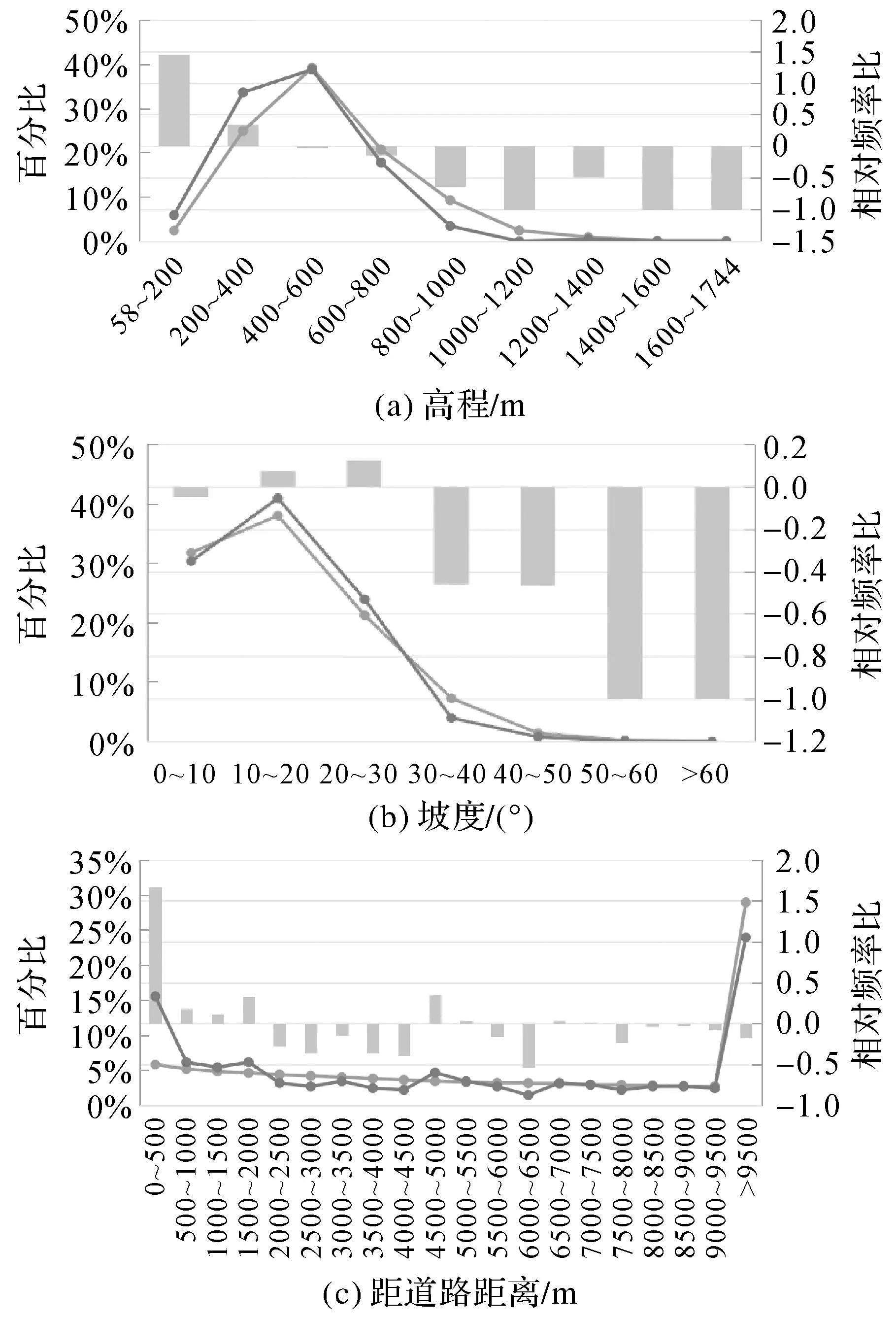
图4 特征因子状态分级Fig.4 Feature factor state grading

(1) 高程。高程是孕育滑坡灾害的条件之一。由图4(a)可知，湘西州的滑坡主要分布在海拔较低的区域，尤其在高程为200～800 m的地区，分布了90%的滑坡灾害点；在高程为58～400 m的地区，滑坡RF值>0，利于滑坡的发生。故将研究区的高程分为5类，分类级别为58～200 m、200～400 m、400～600 m、600～800 m及大于800 m。

(2) 坡度。坡度是造成滑坡的主要特征因子。由图4(b)统计发现，滑坡主要分布在0～30°的坡度范围内，所包含的历史滑坡灾害点占总数的95%以上，尤其在坡度为10～30°的坡度范围内，RF值>0，说明滑坡灾害多发生在10～30°的不稳定斜坡。将研究区内坡度分为4类，分类级别为0～10°、10°～20°、20°～30°及大于30°。

(3) 坡向。不同坡向，光照条件不同，导致植被覆盖度和地表径流等存在差异，从而影响斜坡的稳定性。坡向属于离散型数据，故将研究区坡度分为9类，分类级别为平面、北、东北、东、东南、南、西南、西及西北。

(4) 距道路距离。道路是人类活动因素之一，它体现了人类活动对滑坡灾害的影响。以500 m为步长将距道路距离的数据离散化，如图4(c)所示。由图4(c)可以看出，相较于等步长的区间，在距离道路0～500 m的区域内滑坡灾害点分布数量最多，且RF值最高，说明在该区间内人类工程活动对滑坡灾害的影响程度较大；在距离道路2000～4500 m的区域内，滑坡的RF值相近，故将区间合并；当距离道路5000 m以上时，滑坡的RF值几乎为负数或近于0，说明该区间道路对滑坡灾害的影响程度不大。故本文将道路缓冲区分为7类，分类级别为0～500 m、500～1000 m、1000～1500 m、1500～2000 m、2000～4500 m、4500～5000 m及大于5000 m。

(5) 距河流距离。地表水和地下水的活动容易引起滑坡灾害，这两个因素将直接影响滑坡的稳定性。以200 m为步长将距河流距离的数据离散化，如图4(d)所示。由图4(d)可以看出，在距离河流0～400 m的区间内RF值相对较高，较易发生滑坡灾害；在距离河流1800～2400 m的区间内，滑坡的RF值相近，故将区间合并；当距离河流2400 m以上时，滑坡的RF值全为负数，说明该区间河流对滑坡灾害的影响程度不大。故本文将河流缓冲区分为11个类，分类级别为0～200 m、200～400 m、400～600 m、600～800 m、800～1000 m、1000～1200 m、1200～1400 m、1400～1600 m、1600～1800 m、1800～2400 m及大于2400 m。

(6) 距居民点距离。人类工程活动的增多使得相关的滑坡灾害也日益增多，大部分滑坡与建筑物开挖和道路工程有直接关系。以5000 m为步长将距居民点距离的数据离散化，如图4(e)所示。由图4(e)可以看出，在距离居民点0～30 000 m的区域，分布了82%以上的滑坡灾害点，且在距离居民点0～5000 m的区域内RF值最高，说明在该区间人类工程活动对滑坡灾害的影响程度较大。故将居民点缓冲区分为7类，分类级别为0～5000 m、5000～10 000 m、10 000～15 000 m、15 000～20 000 m、20 000～25 000 m、25 000～30 000 m及大于30 000 m。

(7) 植被指数。植被种类和覆盖情况可以降低滑坡灾害的发生的概率。由图4(f)可以看出，植被指数在-0.1～0时，RF值最高，说明该植被指数范围内较易发生滑坡灾害；植被指数在0～0.4或0.4～0.6时，滑坡的RF值相近，故将区间合并；植被指数在-0.26～-0.1且>0.6时，无滑坡灾害发生。故本文将归一化的植被指数分为5类，分类级别为-0.26～-0.1、-0.1～0、0～0.4、0.4～0.6及大于0.6。

(8) 岩性。地层岩性的物质状态是滑坡发生的可能性和发育成长时间长短的决定性因素。岩性属于离散性数据，故将地层岩性分为7类，分别是第四纪、白垩纪、三叠纪、二叠纪、泥盆纪、志留纪、奥陶纪及寒武纪。

(9) 年累计降雨量。降雨是滑坡发生的主要外部原因。据分析，大雨或连续降雨时期是滑坡灾害发生频次最多的时期。以10 mm为步长将年累计降雨量的数据离散化，由图4(g)可知年累计降雨量在1356～1366 mm和1376～1386 mm时，RF值较高；年累计降雨量分别在1406～1426 mm、1426～1456 mm、1456～1476 mm时，RF值相近，故将区间合并。故将年累计降雨量分为10类，分类级别为1346～1356 mm、1356～1366 mm、1366～1376 mm、1376～1386 mm、1386～1396 mm、1396～1406 mm、1406～1426 mm、1426～1456 mm、1456～1476 mm及1476～1486 mm。

3.1.2 样本选择结果

正样本(滑坡灾害点)数据如图5(a)所示，随机选择负样本(非滑坡灾害点)空间分布如图5(b)所示，CF法选择负样本空间分布如图5(c)所示。结合图6负样本在各类高程中数量可以看出，随机选择负样本方法获取的样本不受高程影响，在空间中分布较为均匀；CF法选择的负样本数量在400～600 m、大于800 m的高程区域明显高于随机选择方法，选取的样本具有较强的稳健性。

图5 样本分布情况Fig.5 Distribution of samples sites

图6 负样本分布情况Fig.6 Distribution of samples sites

3.2 滑坡易发性分区结果分析

为了验证CF法样本选择策略的有效性和MKSVM模型的可靠性。本文对随机选择样本和CF法选择样本分别利用单核SVM模型和MKSVM模型进行试验分析，开展了随机选择样本的单核SVM模型(random slect-support vector mechine,RS-SVM)、随机选择样本的MKSVM模型(random slect-multiple kernel support vector machine,RS-MKSVM)、CF法选择样本的单核SVM模型(certainty factor-support vector mechine,CF-SVM)、CF法选择样本的MKSVM模型(certainty factor-multiple kernel support vector machine,CF-MKSVM)的易发性评价结果。将4种方法的易发性结果分成极低易发区、低易发区、中易发区、高易发区及极高易发区5个分区，结果如图7所示。

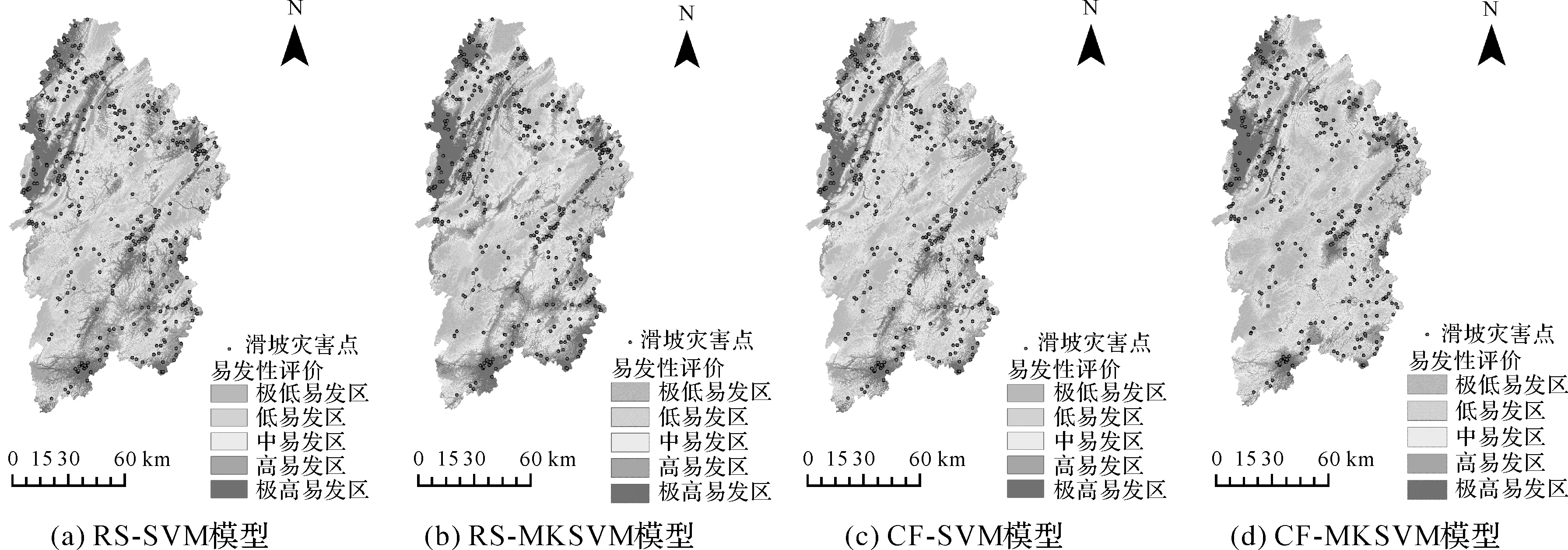
图7 滑坡易发性分析评价结果Fig.7 Evaluation results of landslide susceptibility

由图7可知，极高易发区主要分布在湘西州东南部和西北部，这是因为该区域沟壑纵横、坡度陡峭，地质构造复杂，且被两条主要河流贯穿，再加上日益增多的人类工程活动(如道路工程)，使得该区域极易发生滑坡灾害。对比图7的易发性评价结果可以发现，4种模型的极高易发区和高易发区所占面积逐渐增大，所包含的滑坡灾害点个数逐渐增加，说明相比于图7(a)—图7(c)，图7(d)的CF-MKSVM模型易发性评价结果与滑坡灾害点实际分布规律较为吻合。

3.3 易发分区统计分析

为了便于统计与分析，统一9个特征因子图层的空间参考坐标、栅格大小和栅格行列数。分析并统计训练样本中滑坡灾害点、非滑坡灾害点分别落入5个易发分区的数量以及它们占滑坡灾害点总数、非滑坡灾害点总数的比例。由表2可知，4种方法随着灾害易发性的提高，各分区滑坡灾害点占比亦逐渐增加，在极高易发区达到最大，所占比例依次为55.72%、51.24%、38.31%、31.34%；同时在极低易发区内非滑坡灾害点数量占比比各分区大，所占比例依次为48.01%、40.30%、37.06%、35.07%。可以看出，4种模型方法均能够对滑坡灾害的易发性进行很好的预测，但相比RS-SVM和RS-MKSVM模型，CF-SVM和CF-MKSVM模型精度更高；且相比单核SVM模型，MKSVM模型精度更高。所以，相比其他3种方法，CF-MKSVM模型具备相对较高的预测能力和精度。

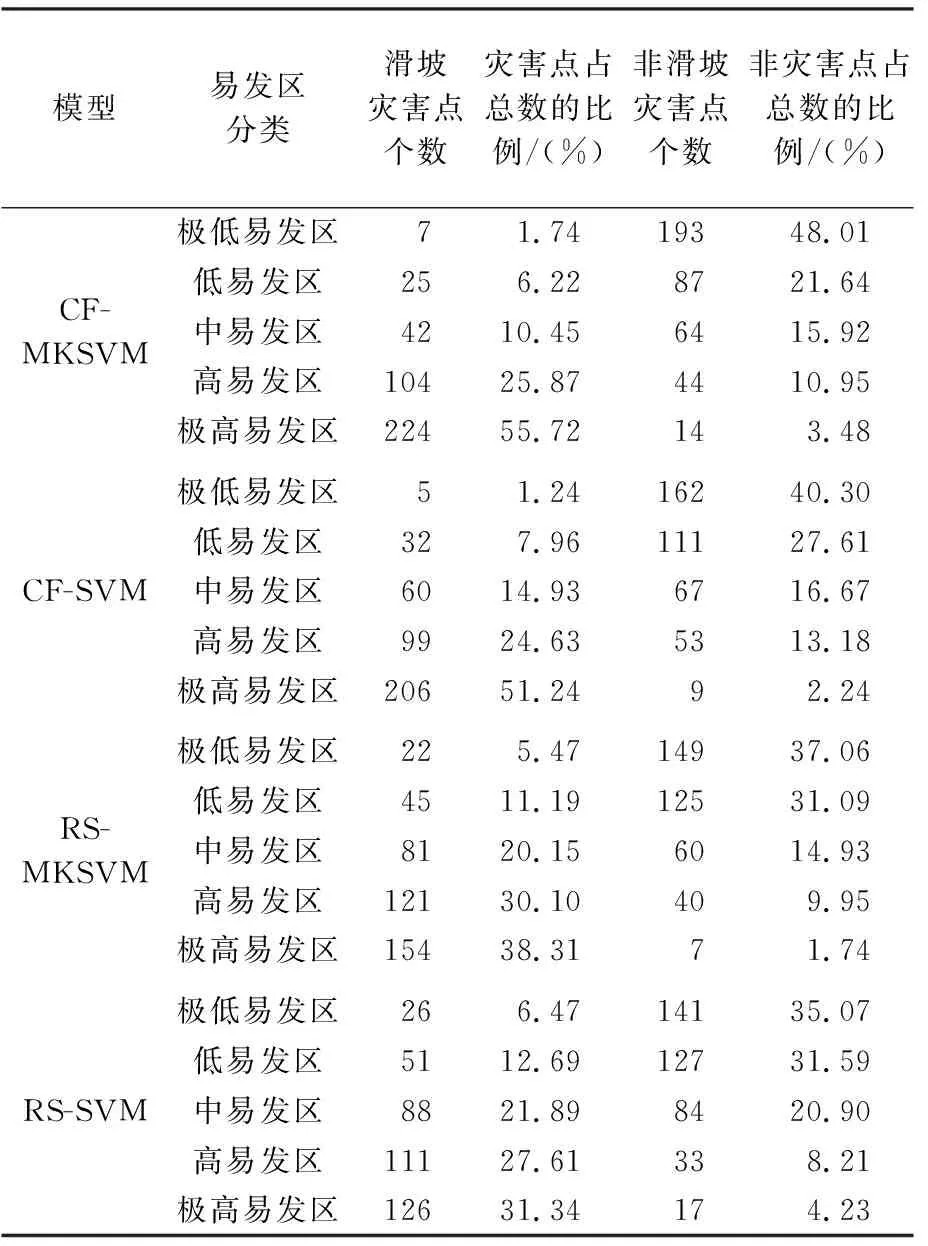
表2 统计分析表

3.4 模型精度验证

为评估本文方法和单核SVM模型的预测精度，本文采用受试者工作特征(receiver operating characteristic,ROC)曲线进行验证[39]，它实际上反映了特异性与灵敏度的关系，是真阳性率与假阳性率的关系图。其背后的逻辑是，如果一项测试没有诊断能力，那么它产生真阳性或假阳性的可能性是相同的。随着诊断能力的增加，即特异性的提升，真阳性率上升，假阳性下降。ROC曲线下的面积(area under curve，AUC)大小代表评价模型精度的大小，面积值越接近1表示评价模型的预测效果越好，面积值等于0.5时无应用价值。4种模型的ROC曲线与AUC值如图8与表3所示。

图8 ROC曲线Fig.8 ROC curve

由图8可知，4种模型都有较好的预测准确率，从细节上来看，CF-MKSVM模型中，离左上角最近的点要比另3种模型ROC曲线中的点距离参考线更远，在一定程度上说明了CF-MKSVM模型要优于另3种模型。

由表3可知，CF-MKSVM模型、CF-SVM模型、RS-MKSVM模型及RS-SVM模型曲线下的面积(AUC值)分别为0.859、0.809、0.798、0.766。由此可见，CF-MKSVM模型相比其余3种评价模型有较高的预测精度，对湘西地区的滑坡易发性分析评价更准确和可靠，为湘西州滑坡灾害治理与决策提供参考依据。

4 结 论

滑坡灾害易发性分析可以为滑坡监测提供重点目标和区域，提高监测效率[40-41]。本文以湖南省湘西州为研究区，分析选取了高程、坡度、坡向、植被指数、距道路距离、距水系距离、距居民点距离、年降雨量及地层岩性9个特征影响因子，验证了滑坡样本质量对滑坡易发性的影响，利用确定性系数法改进了样本选择策略。同时利用多核学习选取SVM最优核函数，对各特征空间最优核函数进行线性组合，提出了顾及样本优化选择的MKSVM滑坡易发性分析评价方法；从滑坡灾害易发性分区图、分区统计及评价模型精度3个方面对CF-MKSVM模型、CF-SVM模型、RS-MKSVM模型、RS-SVM模型进行了对比分析。试验结果表明：①负样本选择质量影响滑坡易发性分析精度；②本文提出的CF样本选择策略提高了负样本选择质量，改进了滑坡灾害易发性评价模型训练精度；③相比单一核函数的SVM模型，MKSVM模型通过多特征映射选取最优线性核函数，从而提高了模型的分类准确率和预测精度；④CF-MKSVM模型预测精度优于其他3种模型的预测精度，具有较高的准确性、可靠性，对减少滑坡灾害带来的损失，提高滑坡灾害防治工作的效率具有重要理论意义与实际价值。