时空Kalman滤波在变形分析中的应用研究
2022-11-04戴吾蛟晏慧能
石 强,戴吾蛟,晏慧能,刘 宁
1. 中南大学测绘与遥感科学系,湖南 长沙 410083; 2. 江苏海洋大学海洋技术与测绘学院,江苏 连云港 222005; 3. 湖南省精密工程测量与形变灾害监测重点实验室,湖南 长沙 410083
随着传感器网络、GNSS、InSAR等现代变形监测技术的发展,人们获取了大量的变形数据[1-3],这些变形数据具有较为复杂的时空相关性,传统的空间和时间序列分析方法已无法满足时空变形分析的需求,因此一些学者开始将时空数据处理的理论与方法(例如时空地统计学模型、时空自回归模型、时空地理加权回归模型及时空Kalman滤波等)引入变形分析领域[4]。时空地统计学模型是在传统地统计学的基础上,运用时空插值及随机模拟估算和量化时空变化,动态反映地理空间的变化过程,其代表性的方法是时空克里金,在边坡[5-6]及隧道围岩[7]变形分析中得到了较好的应用。时空克里金模型虽然同时考虑了变形数据的时间和空间相关性,但是它计算量较大,不能满足变形监测大数据时空分析的需求。时空自回归模型是根据空间权矩阵及AR模型描述时空数据的时空相关性,已用于大坝[8-9]、桥梁[10]、地下管线[11]及建筑物[12]时空变形预测,且具有较高的预测精度,但是该模型分别考虑空间和时间上的相关性,并不是真正意义上的时空分析模型。时空地理加权回归模型是在普通地理加权回归模型的基础上进行时空扩展,构建了顾及时空相关性的时空回归模型,它已被用于大坝变形分析[13-14],但是该模型需要对监测点的位移与影响因素建立多元变系数回归关系,计算量也较大。时空Kalman滤波是一种融入空间模型的Kalman滤波方法,在时空数据分析方面具有很大的优越性,能对时空数据进行时空动态滤波、时空插值及时空预测,已被广泛应用于众多时空数据分析领域,如传染病动态演变[15]、遥感影像融合[16]、空气污染物建模[17]、气候变化[18]等领域。文献[19]提出了第一个具有统计意义的时空Kalman滤波,发展形成了3种代表性的时空Kalman滤波模型:Kriged Kalman filter(KKF)模型[20]、space time Kalman filter(STKF)模型[21]、spatio-temporal mixed effects (STME)[22-23]模型。文献[24—27]将时空Kalman滤波引入变形监测领域,并在动态滤波插补GPS地面沉降数据、融合GNSS和InSAR沉降数据获取高时空分辨率地表沉降数据及大坝变形的时空预测方面取得了良好的应用效果。但上述研究仅对时空Kalman滤波用于变形分析进行了初步探索,未对已有典型的时空Kalman滤波模型的理论及其在变形分析中的适用性进行深入分析。
为了更好地利用时空Kalman滤波进行时空变形分析,本文从基本原理及试验两方面对比分析KKF、STKF及STME 3种典型时空Kalman滤波模型的异同点及其在变形分析应用中的适用性,并对比分析其在时空滤波去噪、数据插补及变形预测3方面的应用效果。
1 基本原理
1.1 KKF基本模型
KKF模型是将泛Kriging插值法与Kalman滤波结合在一起的时空Kalman滤波模型,其基本模型如式(1)所示
(1)
式中,Zt(s)表示t时刻位置s处的观测值;αt为状态量;εt(s)~N(0,R1),为观测噪声;Φ为状态转移矩阵;wt~N(0,Q1),为状态噪声;H为描述空间相关性的空间场,由式(2)—式(5)确定[20,26],H(S)′为H(s)的转置,为便于描述,下文将H(s)简记为H
B=Σ-1-Σ-1X(X′Σ-1X)-1X′Σ-1
(2)
式中,Σ为协方差矩阵;X为趋势场;X′为X转置。
为降维运算,将式(2)中的B进行谱分解,得到
(3)
式中,U=(u1,u2,…,un),为B的特征向量;U′为U的转置;D=diag(d1,d2,…,dn),为对应的特征值。
则式(1)中的空间场H可表示为
(4)
式中,σ(s0)为协方差矢量;Hj表示空间场的前q个元素为趋势场,代表空间的整体变异;Hk表示空间场的p-q个元素为主要场,代表空间的局部变异。其中,当式(5)设定某个值时(如90%或95%),可以得到p的值
(5)
1.2 STKF基本模型
KKF模型没有顾及空间小尺度细微变异,其建模结果过于光滑[28]。针对这个问题,文献[21]提出了顾及小尺度细微变异的STKF模型,其模型为
(6)
式中,Zt(s)表示t时刻位置s处的观测值;S(s)为描述空间相关性的正交空间基;αt为状态量;ξ(s,t)~N(m,U2),表示具有空间相关性的小尺度细微变异;εt(s)~N(0,R2),为观测噪声;Φ为状态转移矩阵;J=[S(s)′S(s)]-1S(s),为状态噪声的系数矩阵;ηt~N(0,Q2),为状态噪声。
1.3 STME基本模型
针对KKF及STKF模型存在海量数据计算困难的问题,文献[22—23]提出了固定秩的STME模型,其模型为
(7)
式中,Zt(s)表示t时刻位置s处的观测值;μt(s)为趋势项;S(s)为描述空间相关性的空间基;αt为状态量;ξt(s)~N(0,U3),表示小尺度细微变异;εt(s)~N(0,R3),为观测噪声;Φ为状态转移矩阵;ηt~N(0,Q3),为状态噪声。
1.4 时空动态变形建模方法
3种时空Kalman滤波模型的建模方法类似,均是先基于观测数据估计模型未知参数,然后基于估计的未知参数进行时空动态变形分析。本节以KKF模型为例,介绍利用时空Kalman滤波进行时空动态变形分析的具体建模方法,其建模方法主要包含构建空间场、估计模型未知参数及变形分析3部分。
1.4.1 构建KKF模型空间场H
由式(4)可知,KKF模型空间场H的前q个元素为趋势场X,一般将测站的位置坐标(如经纬度)设为X的值。选定趋势类型(常数趋势、线性趋势或二次曲面趋势)后,利用最小二乘法估计趋势场的系数矩阵β。空间场H剩余的p-q个元素(主要场)可根据式(2)—式(5)计算,具体计算过程如下:
(1) 从原始观测数据中去除趋势项,得到剩余残差v=Zt(s)-Xβ;利用变差函数(常用的变差函数模型有高斯模型、球状模型、指数模型)拟合残差v的空间变异,基于拟合的变差函数求取所有已知测站之间的协方差矩阵Σ。
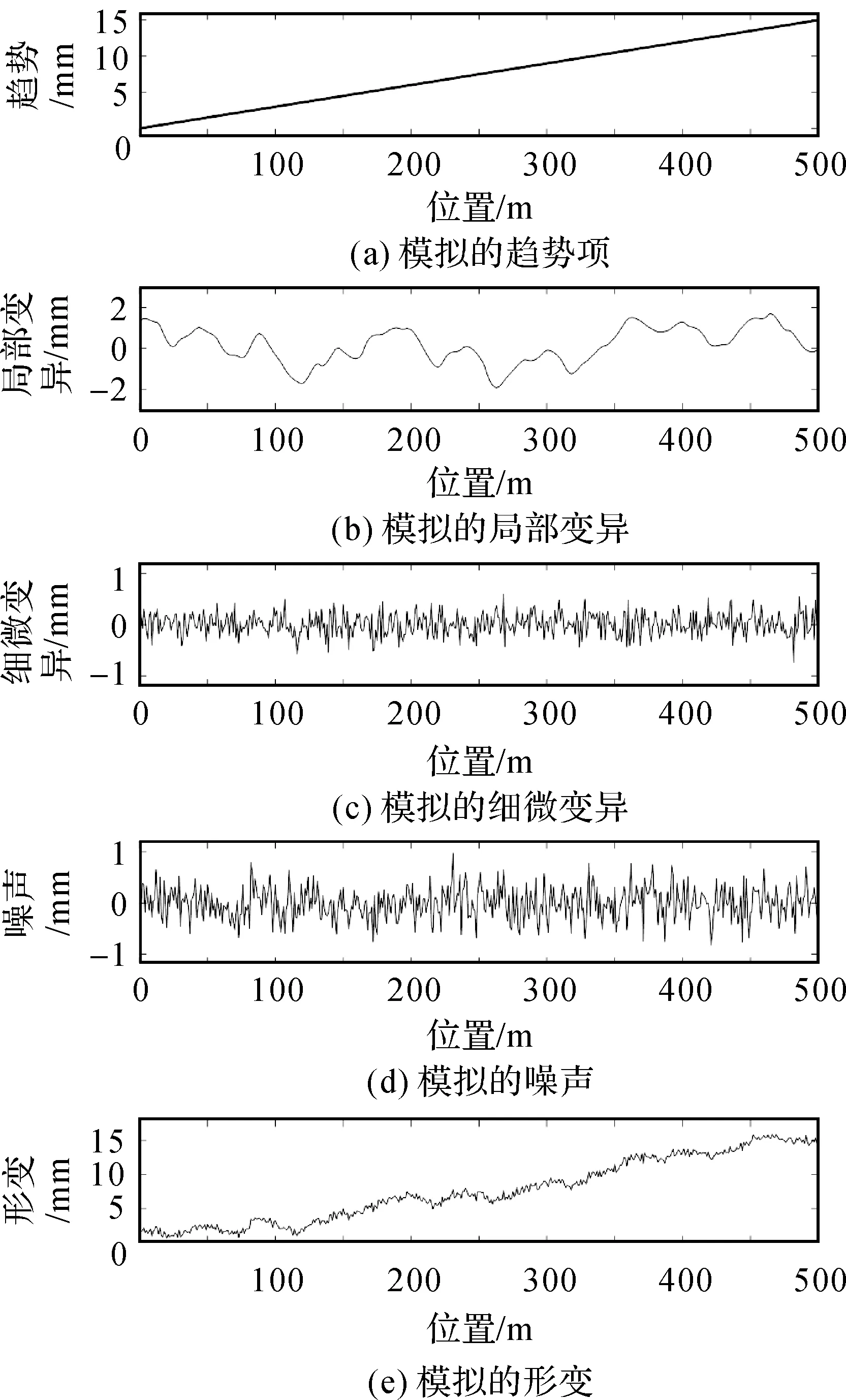
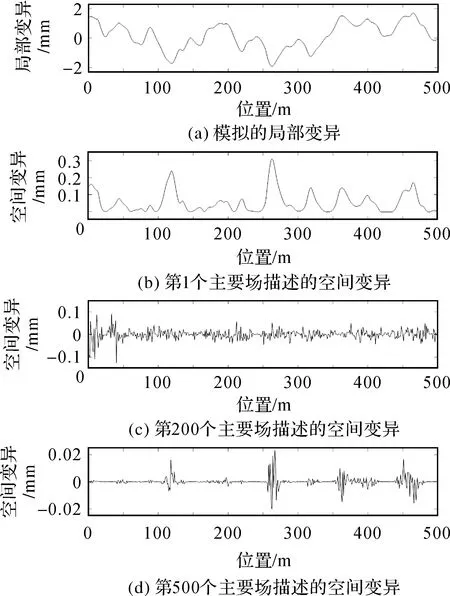
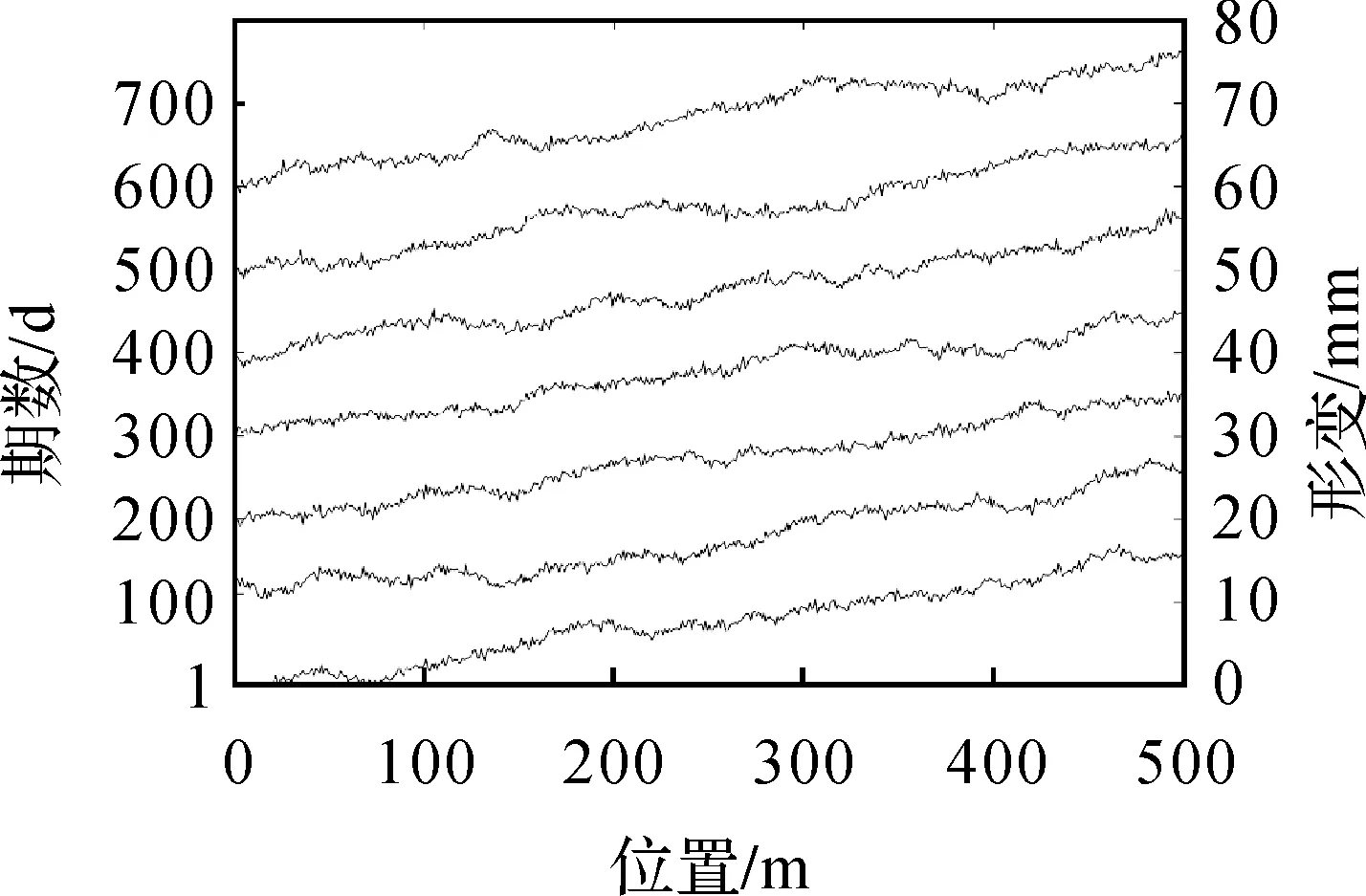
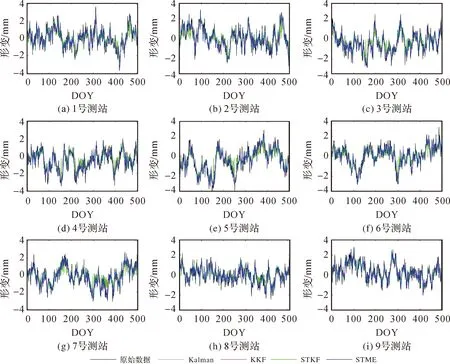
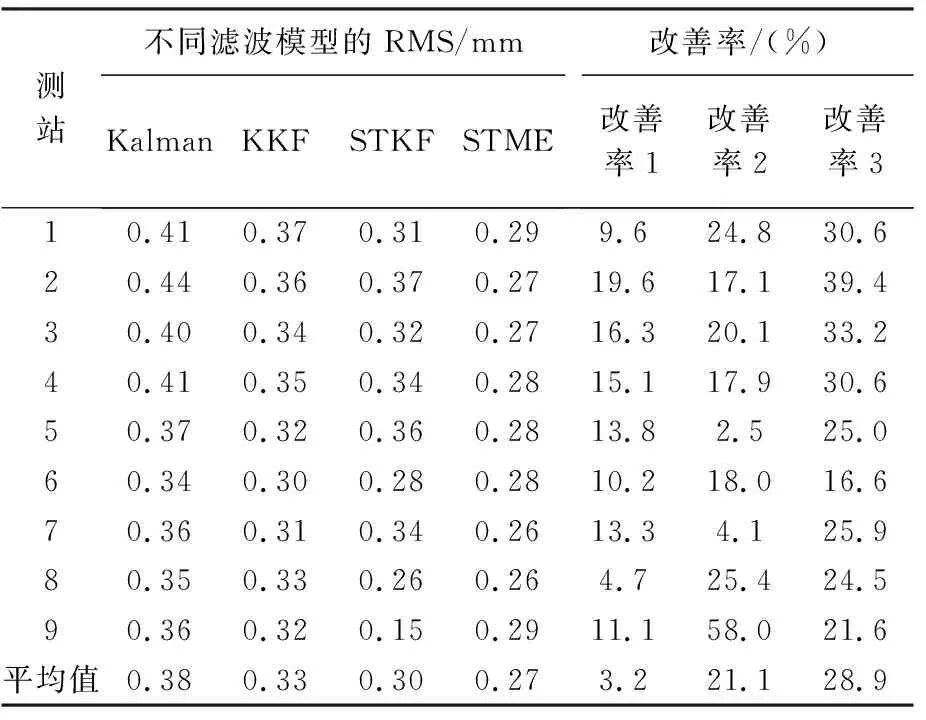
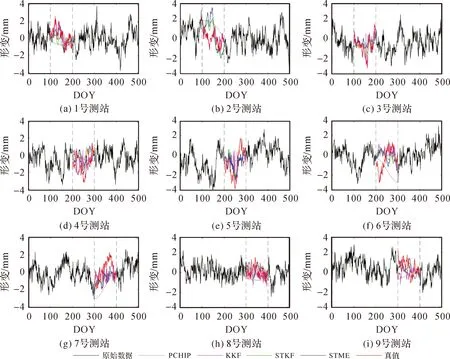
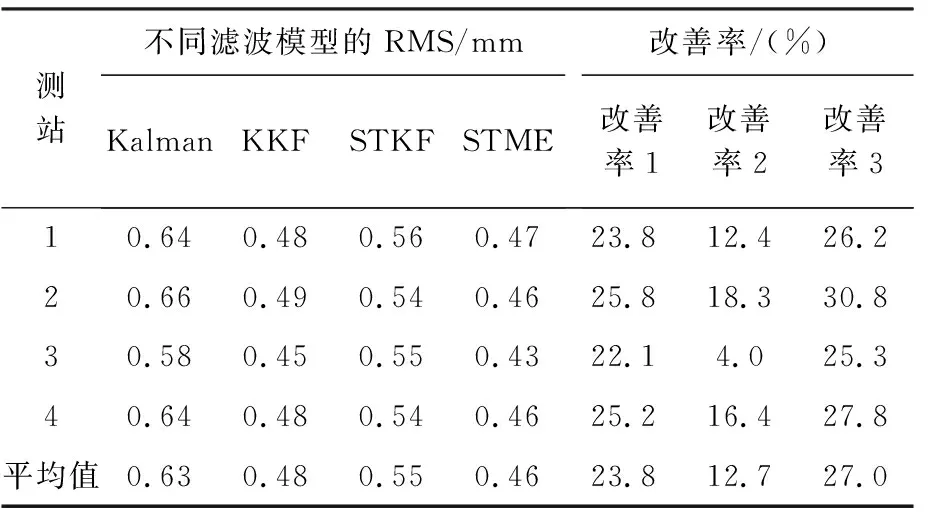
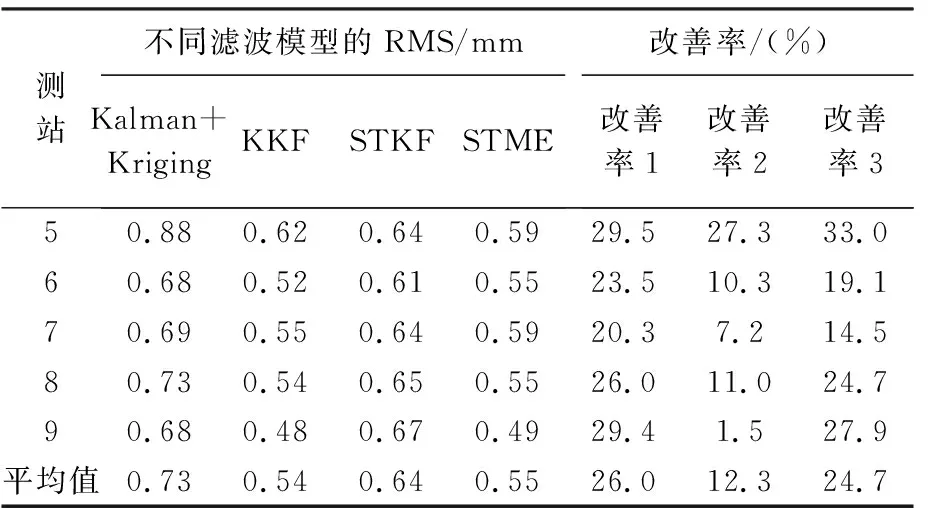
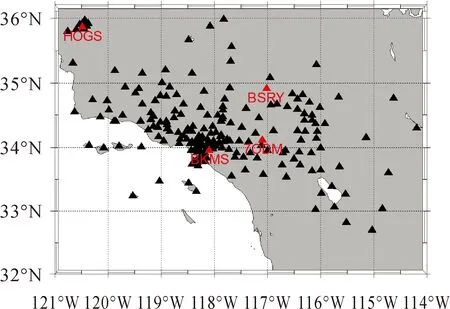
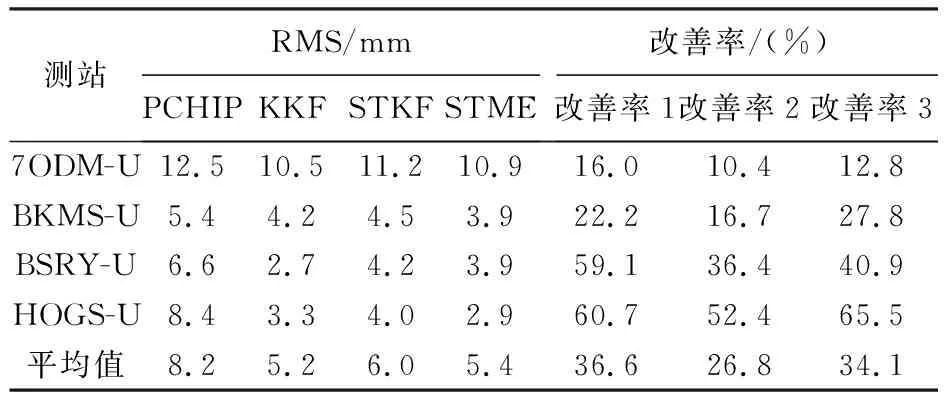
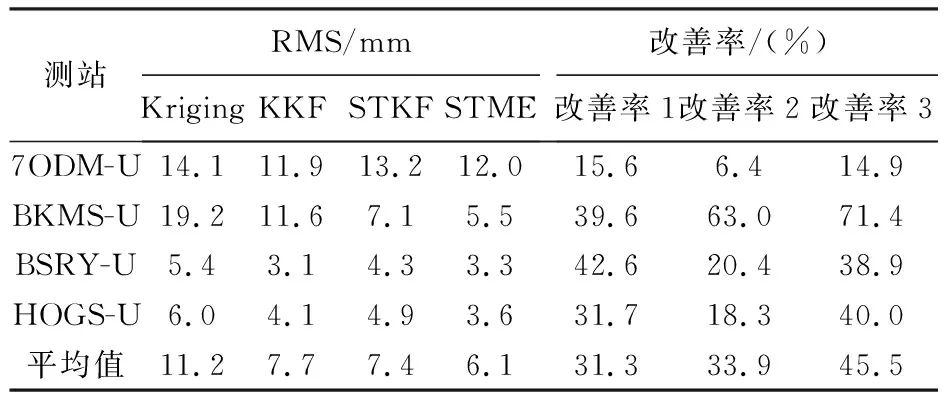
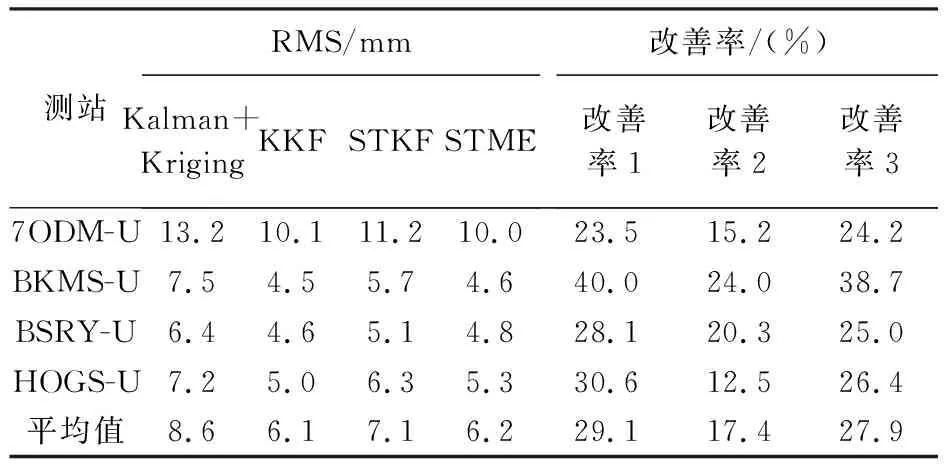
(2) 根据式(2)和式(3)获得矩阵B的特征值及特征向量,将式(3)得到的特征值D=diag(d1,d2,…,dn)进行非降序排列,即0=d1=d2=…=dq (3) 将空间位置s0的位置坐标代入拟合的变差函数即可求得σ(s0)′,并将p的值代入式(4)可求解空间场H的主要场Hk。将求得的趋势场Hj和主要场Hk组合即可得到KKF模型的空间场H=[Hj,Hk]。 假定式(1)中状态量αt的初始状态为α0~N(a0,P0),由KKF模型的基本原理可知,KKF模型的未知参数为Ψ=[Φ,R1,Q1]。通过经验设定未知参数的初始值,利用EM(expectation-maximum)[22]算法迭代估计未知参数的最佳估值。 对于t=1,2,…,T,向前滤波形式如下 αt|t-1=Φαt-1|t-1 (8) Pt|t-1=ΦPt-1|t-1Φ′+Q1 (9) K=Pt|t-1H′(HPt|t-1H′+R1)-1 (10) αt|t=αt|t-1+K(Zt(s)-Hαt|t-1) (11) Pt|t=Pt|t-1-KHPt|t-1 (12) 当获得未知参数最优估计值后,可通过式(13)获得监测站观测数据的滤波值、缺失数据的插补值及未进行实际观测站点(简称非观测站点)当前时刻的空间预测值 (13) 监测站点与非观测站点未来时刻变形数据的预测值可由式(14)计算得到 (14) 由式(1)—式(7)可以看出,KKF、STKF及STME模型虽然是3种不同的时空Kalman滤波模型,其时空数据相关性描述方式基本相同,具体包括:①均是基于一阶矢量自回归的动力学模型描述时空数据的时间相关性;②均是利用空间基函数描述时空数据的空间相关性;③均是利用空间基函数及动力学模型组合形式描述时空数据的时空相关性。 同时也可以看出,3种模型在趋势项、小尺度细微变异、观测噪声、空间基函数、状态转移矩阵计算及降维方法6方面存在差异,具体有:①KKF和STME模型包含趋势项μt(s),STKF模型不包含趋势项,建立STKF模型时需要先去除数据的趋势。②KKF模型不包含小尺度细微变异,将小尺度细微变异建模在观测噪声中。STKF和STME模型在观测方程中单独建立小尺度细微变异ξt(s)。STKF模型的小尺度细微变异为空间相关的有色噪声,STME模型的小尺度细微变异为空间不相关的高斯白噪声。③KKF模型的观测噪声包含小尺度细微变异及观测误差,STKF和STME模型的观测噪声是高斯白噪声。④KKF模型的空间基函数H是根据式(2)—式(5)构建的。STKF和STME模型的空间基函数S(s)的选择具有多样性,需要根据经验选择合适的空间基函数。其中,STKF模型的空间基函数必须是正交的,而STME模型的空间基函数无正交性限制。⑤STKF模型通过时空交互函数来构建状态转移矩阵Φ,KKF和STME模型的状态转移矩阵可根据具体的应用情况灵活选择,一般情况下,将KKF和STME模型状态转移矩阵的初始值设为单位阵,然后通过EM估计方法求解其最佳估计值。⑥KKF模型基于式(5)选取特定的特征值实现降维功能,STKF及STME模型基于选取的空间基函数对时空数据进行降维。 由以上理论分析可知,KKF、STKF和STME这3种模型的主要差异在于空间变异的描述形式。为进一步分析3种模型对空间变异描述的精细程度,笔者模拟了一组空间数据,并分别用KKF、STKF和STME这3种模型对模拟数据进行空间变异建模拟合,以拟合残差作为指标对比分析3种模型对空间变异的表达能力。 2.2.1 模拟数据 模拟的空间变形数据由趋势项、局部变异项、细微变异项及噪声项组成,具体如下。 (1) 趋势项:采用一个与空间位置线性相关的趋势,即μt(s)=0.03·s,其中0 m≤s≤500 m。 (15) (16) 利用以上方法模拟的空间数据如图1所示。 图1 模拟的空间变形数据Fig.1 The simulated spatial deformation data 2.2.2 KKF模型空间变异拟合效果分析 由图1可知,模拟数据包含与空间位置相关的线性趋势项,因此式(4)中的趋势场设为:Hj=Xj,j=1,2,…,500,其中Xj为位置坐标。根据式(2)和式(3)可计算式(4)的主要场Hk。为了分析特征值与主要场的关系,本文对比分析了第1个主要场、第200个主要场及第500个主要场描述的空间变异与局部变异之间的关系,如图2所示。 图2 模拟数据的局部变异及KKF主要场Fig.2 Local variations of simulated data and principal field of KKF model 对比图2中的局部变异及第1、200、500个主要场描述的空间变异,可以看出,KKF建模的第1个主要场能描述较多的空间变异;第200个主要场描述的空间变异较第1个主要场少;第500个主要场仅描述部分区域(100~150 m、250~300 m、350~400 m及450~470 m)的空间变异。本文试验的第1个主要场对应最小的特征值,第500个主要场对应最大的特征值。通过上述分析可知,较小的特征值能描述大尺度空间变异,较大的特征值描述小尺度空间变异。因此,KKF建模过程中保留的特征值越多,越能有效地描述空间变异。但是当数据量较大时,保留的特征值越多,其计算量越大。为了减轻计算压力,通常根据式(5)选取部分特征值参与建模。本文试验中,若仅建模90%的空间变异(即ratio=0.9),由式(5)可得至少需要保留451个特征值,空间拟合及残差如图3所示。由图3可知,KKF能有效地描述空间变异,其拟合残差的RMS值为0.25 mm。 图3 KKF空间变异拟合结果及残差Fig.3 Spatial modeling results and residuals of KKF model 2.2.3 STKF模型空间变异拟合效果分析 由1.2节可知,STKF模型利用正交的空间基函数描述时空数据的空间相关性,本文试验基于经验正交函数构建STKF模型的空间基函数。式(6)的STKF模型不包含时空数据的趋势项,因此在空间建模拟合之前需要去除观测数据的趋势项。采用最小二乘方法去除模拟数据的趋势项,得到模拟数据的局部变异ν。基于矩估计求取局部变异ν的经验协方差矩阵Q=E(νν′)-R,其中R表示观测噪声方差。将Q进行特征分解:Q=ΨΛΨ′,其中Ψ=[ψ1,ψ2,…,ψn]为特征向量,Λ=diag(λ1,λ2,…,λn)为特征值。本文试验将特征向量ψi按降序排列,并选取前n个特征向量作为STKF模型的空间基。类似于2.2.2节,本文对比分析了前3个空间基描述的空间变异与局部变异之间的关系,如图4所示。 由图4可以看出,STKF模型第1个空间基的变化趋势与模拟数据的局部变异趋势非常相似,表明第1个空间基就可以描述局部变异的整体变化趋势。第2个空间基和第3个空间基仅描述了部分区域的空间变异,表明少量的空间基即可描述观测数据的空间变异,因此STKF模型的降维效果明显优于KKF模型。为了分析STKF模型对空间变异的建模效果,本文试验选取了前200个STKF空间基对模拟数据进行空间拟合,其拟合效果如图5所示。 图4 局部变异及STKF空间基Fig.4 Local variations of simulated data and spatial basis function of STKF model 图5 STKF模型空间变异拟合结果及残差Fig.5 Spatial modeling results and residuals of STKF model 由图5可知,前200个STKF空间基能有效地描述本文试验模拟数据的空间变异,其拟合残差的RMS值为0.24 mm。对比KKF模型的空间拟合效果可以看出,STKF模型基于少量空间基函数即可获得优于较多空间基函数的KKF空间变异拟合效果,表明STKF模型的降维效果明显优于KKF模型。 STKF模型的空间基在描述空间变异方面存在一个问题:最主要的空间基描述了固定的空间变异,然而在实际应用中,空间变异是不断变化的,导致最主要的空间基无法描述新的空间变异。例如在地表变形过程中,前期数据仅有一处区域存在沉降漏斗(记为区域A),而后期数据中区域A的沉降漏斗已无变形,区域A外的其他区域又出现一个新的沉降漏斗(记为区域B)。在建立STKF模型时,根据前期的变形数据选取最主要的空间基,由于前期数据中区域B内无变形,因此选取的空间基将不会包含区域B的变形信息,选定的空间基也无法描述区域B后期发生的变形。 2.2.4 STME模型空间变异拟合效果分析 STME模型同样需要先去除趋势项,然后对去除趋势后的大尺度局部变异及小尺度细微变异进行建模。本文试验选取bisquare空间基[25]作为STME模型的空间基,bisquare空间基形式如下 (17) 式中,ck为第k层尺度下的空间基位置;gk为第k层尺度下变异函数的变程(一般将第k层尺度下最短距离的1.5倍作为变程)。为了准确描述空间变异,一般从多个尺度布设空间基函数,直至式(18)的空间基拟合残差趋于平稳 V=Zt(s)-μt(s)-S((S′S)-1S′(Zt(s)- μt(s))) (18) 本文试验共设置3个尺度的空间基,其中第1个尺度下的空间基位置为:c1=(1+60i),i=0,1,…,8;第2个尺度下的空间基位置为:c2=(2+20i),i=0,1,…,24;第3个尺度下的空间基位置为:c3=(3+5i),i=0,1,…,99;共布设134个空间基。STME模型空间基拟合效果如图6所示。 由图6中可以看出,空间基的拟合效果与原始观测数据趋势一致,能较好地描述原始数据的空间变异,但是空间基拟合后的残差中仍存在较大的空间变异。笔者将残差中的空间变异建模为式(7)中的小尺度细微变异ξt(s),利用球状模型的变异函数描述小尺度细微变异ξt(s)的协方差矩阵。将求取的小尺度细微变异ξt(s)加入空间基拟合结果中,得到STME模型的结果,如图7所示。 对比图6与图7可知,加入小尺度细微变异ξt(s)后,STME模型的空间拟合结果与原始观测数据更吻合,其拟合残差更稳定,残差RMS值为0.21 mm。对比本文试验3种时空Kalman滤波模型的拟合残差可以看出,3种时空Kalman滤波模型对空间变异的拟合效果基本相当。 图6 空间基拟合结果及残差Fig.6 Spatial modeling results and residuals of spatial basis function 图7 STME模型空间变异拟合结果及残差Fig.7 Spatial modeling results and residuals of STME model 3.1.1 时空变形模拟数据 模拟的时空变形数据由趋势项、局部变异项、细微变异项及噪声项组成,其中趋势项与2.2.1节模拟的空间变形监测数据的趋势一致,在2.2.1节细微变异和噪声项的基础上分别模拟600期的细微变异和噪声项。在2.2.1节局部变异的基础上,采用随机游走模型模拟时空变形监测数据的局部变异,即ηt=Hηt-1+δt,t=1,2,…,600 d。空间基S乘以每一期的状态量得到每一期变形监测数据的真值。为了展示模拟的时空变形监测数据,以100 d为时间间隔均匀选取7期的模拟数据,抽取的每期变形数据在前一期变形数据基础上加10 mm,如图8所示。 图8 模拟的时空变形数据Fig.8 The simulated spatio-temporal deformation data 3.1.2 滤波去噪效果分析 从模拟的时空变形数据中随机选取20个测站作为已知测站,利用选取的20个已知测站数据分别建立KKF、 STKF及STME模型。从20个已知测站中随机选取9个测站分析3种时空Kalman滤波模型的滤波去噪效果,为对比分析3种时空Kalman滤波模型的滤波效果,本文利用普通Kalman滤波对选取的变形数据进行滤波去噪。时空Kalman滤波模型的滤波结果及普通Kalman滤波结果如图9所示,其滤波结果残差的RMS统计见表1。 图9 时空Kalman滤波模型及普通Kalman滤波模型的滤波结果Fig.9 Filtering results of spatio-temporal Kalman filter and Kalman filter 表1中改善率1、改善率2、改善率3分别表示KKF、STKF及STME模型滤波结果相对于普通Kalman滤波结果的改善率。由表1可知,3种时空Kalman滤波模型均能有效地去除观测数据的噪声,其时空滤波结果相对于普通Kalman滤波结果的平均改善率分别为13.2%、21.1%、28.9%。 表1 滤波结果残差RMS统计 3.1.3 缺失数据插补效果分析 将上一节选取的9个已知测站数据连续缺失100 d,然后利用20个已知测站数据分别建立KKF、STKF及STME模型,并对选取的9个已知测站缺失的100 d数据进行时空插值。为对比分析3种时空Kalman滤波模型的时空插值效果,笔者利用分段三次Hermite插值多项式(PCHIP)插值出缺失的变形数据。时空插值结果及PCHIP插值结果如图10所示,其插值结果残差的RMS统计见表2。 图10 时空Kalman滤波模型时空插值及PCHIP时间插值结果Fig.10 The interpolation results of spatio-temporal Kalman and PCHIP 图10中每幅图内灰色竖虚线表示缺失数据的时间段,表2的改善率1、改善率2、改善率3分别表示KKF、STKF及STME模型时空插值结果相对于PCHIP插值结果的改善率。由图10及表2可知,3种时空Kalman滤波模型均能有效地插补缺失的观测数据,其时空插值结果相对于PCHIP插值结果的平均改善率分别为61.0%、32.2%、33.9%。 表2 时空Kalman滤波模型时空插值及PCHIP时间插值结果残差RMS统计 3.1.4 空间预测效果分析 时空Kalman滤波既可以基于已知测站变形数据的时空相关性预测非观测站点当前时刻的变形数据,也可以预测变形体的未来发展趋势。为了便于区分,本文将非观测站点当前时刻变形数据的时空预测记为空间预测,将未来时刻变形数据的时空预测记为时空预测。本节基于模拟的时空变形数据检验3种时空Kalman滤波模型的空间预测性能。 利用20个已知测站DOY 1—DOY 500的数据分别建立KKF、STKF及STME模型,从未参与建模的480个测站中随机选取9个测站作为验证测站,基于建立的时空Kalman滤波模型预测9个验证测站DOY 1—DOY 500的变形数据,为对比分析3种时空Kalman滤波模型的空间预测效果,笔者利用普通Kriging模型插值出9个验证测站的变形数据。3种时空Kalman滤波模型空间预测结果及普通Kriging模型空间插值结果如图11所示,其预测结果残差的RMS统计见表3。 图11 时空Kalman滤波模型空间预测及Kriging空间插值结果Fig.11 Results of spatio-temporal Kalman and Kriging 表3 时空Kalman滤波模型空间预测及Kriging空间插值结果残差RMS统计 表3的改善率1、改善率2、改善率3分别表示KKF、STKF、STME模型空间预测结果相对于Kriging空间插值结果的改善率。由图11及表3可知,3种时空Kalman滤波模型均能有效地预测非观测站点当前时刻的变形数据,其空间预测结果相对于Kriging空间插值结果的平均改善率分别为66.7%、64.0%、66.0%。 3.1.5 时空预测效果分析 时空Kalman滤波既可以预测已知测站未来时刻的变形数据,也可以预测非观测站点未来时刻的变形数据。本节分别利用时空Kalman滤波预测已知测站和非观测站点未来时刻的变形数据,并对比分析其时空预测精度。本文仅对比分析了单步预测结果,即利用前期变形数据仅预测下一天的变形,然后基于新观测的变形数据更新模型参数,继续预测下一天的变形。 利用20个已知测站DOY 1—DOY 500的变形数据分别建立KKF、STKF及STME模型,从未参与建模的480个测站中随机选取5个测站作为验证测站(非观测站点),基于建立的时空Kalman滤波模型对20个已知测站及5个验证测站未来100 d(DOY 501—DOY 600)的变形数据进行时空预测。为对比分析3种时空Kalman滤波模型对未来变形数据的时空预测效果,笔者利用普通Kalman滤波对20个已知测站未来100 d的变形数据进行时间预测,利用Kalman滤波+Kriging组合模型对5个验证测站(非观测站点)未来100 d的变形数据进行时间和空间预测。从20个已知测站中随机选取4个测站的预测结果进行对比分析,4个已知测站及5个验证测站(非观测站点)未来100 d的预测结果如图12所示。4个已知测站预测结果残差的RMS统计见表4,5个验证测站预测结果残差的RMS统计见表5。 图12 已知测站及非观测站点未来100天变形数据的预测结果Fig.12 Prediction results of known and unknown stations for the next 100 days 表4 已知测站时空Kalman滤波模型时空预测及Kalman滤波模型时间预测结果残差RMS统计 表5 非观测站点时空Kalman滤波模型时空预测及Kalman+Kriging组合模型预测结果残差RMS统计 图12(a)—(d)表示4个已知测站的时空Kalman滤波模型时空预测结果和普通Kalman滤波时间预测结果,图12(e)—(i)表示5个验证测站的时空Kalman滤波模型时空预测结果和Kalman滤波+Kriging组合模型预测结果。表4的改善率1、改善率2、改善率3分别表示KKF、STKF及STME模型时空预测结果相对于普通Kalman滤波时间预测结果的改善率。由图12可以看出,3种时空Kalman滤波模型预测的已知测站未来变形与真实变形的变化趋势一致。由表4的RMS统计可知,3种时空Kalman滤波模型均能有效地基于已知测站时空变形数据预测已知测站未来时刻的变形数据,其时空预测结果相对于普通Kalman滤波时间预测结果的平均改善率分别为23.8%、12.7%、27.0%。 表5的改善率1、改善率2、改善率3分别表示KKF、STKF及STME模型时空预测结果相对于Kalman滤波+Kriging组合模型预测结果的改善率。由表5及图12可知,KKF、STKF及STME模型对非观测站点未来变形的时空预测结果与真实变形吻合较好,其时空预测结果相对于Kalman滤波+Kriging组合模型预测结果的平均改善率分别为26.0%、12.3%、24.7%。对比表4和表5时空预测结果残差的平均RMS值可以看出,非观测站点时空预测结果的平均RMS值略高于已知测站时空预测结果的平均RMS值。其主要原因是已知测站通过观测数据更新建立的时空Kalman滤波模型,使其与实测数据更吻合,而非观测站点的时空预测结果是基于建立的时空Kalman滤波模型进行时空预测的,无实际观测数据对模型预测数据进行修正。 为进一步对比分析3种时空Kalman滤波模型在变形分析中的应用效果,本节选取了南加州地区GPS地面沉降数据进行处理与分析。从SCIGN网站(http:∥www.scign.org/)下载了2005年1月1日—2007年1月1日共731 d的南加州综合GPS监测网中209个测站的沉降数据,选取数据缺失较少的4个GPS站点(7ODM、BKMS、BSRY和HOGS)作为验证测站,其测站位置分布如图13所示。 图13 南加州GPS测站位置分布Fig.13 Location distribution of GPS stations in Southern California 由于实际的变形数据含有观测噪声,无法定量分析3种时空Kalman滤波模型的滤波去噪精度,因此本节基于南加州地区GPS地面沉降数据定量地对比分析3种时空Kalman滤波模型在缺失数据插补、空间预测及时空预测3方面的应用效果。 将4个验证测站连续删除200 d的沉降数据模拟大量缺失的GPS变形序列,利用PCHIP、KKF、STKF及STME模型插补缺失的数据,其插值结果残差的RMS统计见表6。利用205个GPS测站DOY 1—DOY 731的沉降数据分别建立Kriging、KKF、STKF及STME模型,并预测4个验证测站DOY 1—DOY 731的沉降数据,其预测结果残差的RMS统计见表7。利用205个GPS测站DOY 1—DOY 631的沉降数据分别建立Kalman滤波+Kriging组合模型、KKF、STKF及STME模型,并预测4个验证测站未来100 d(DOY 632—DOY 731)的沉降数据,其预测结果残差的RMS统计见表8。 由表6、表7及表8可知,3种时空Kalman滤波模型对于实测变形数据的缺失数据插补精度、空间预测精度及时空预测精度均优于普通模型的插补及预测精度,进一步检验了3种时空Kalman滤波在变形分析应用中的有效性。 表6 时空Kalman滤波模型时空插值及PCHIP时间插值结果残差RMS统计 表7 时空Kalman滤波模型空间预测及Kriging空间插值结果残差RMS统计 表8 时空Kalman滤波模型空间预测及Kalman+Kriging组合模型预测结果残差RMS统计 本文从基本原理和试验两方面对比分析了3种典型时空Kalman滤波模型的异同点及其在变形分析中的适用性和应用效果。理论上,3种时空Kalman滤波模型均基于空间基函数及动力学模型组合形式描述时空数据的时空相关性,其主要差异在于空间变异的描述形式,如空间数据的趋势项、小尺度细微变异、观测噪声及空间基函数。在时空变形分析应用效果方面,3种时空Kalman滤波模型均具有较高精度的时空滤波、时空插值及时空预测性能:KKF模型降维效果不明显,更适合于监测点稀疏(如GNSS监测)的时空变形分析应用;STKF模型和STME模型降维效果明显,更适合于海量测站(如InSAR监测或GNSS与InSAR集成监测等)的时空变形分析应用。但STKF模型的空间基描述了固定的空间变异,无法适用于复杂变形规律的变形分析,因此优先选用STME模型用于海量测站的时空变形分析。1.4.2 估计未知参数
1.4.3 时空变形分析应用
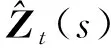

2 3种时空Kalman滤波模型比较分析
2.1 理论分析
2.2 试验分析
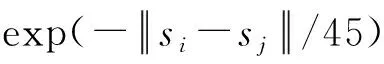
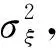
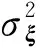
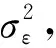
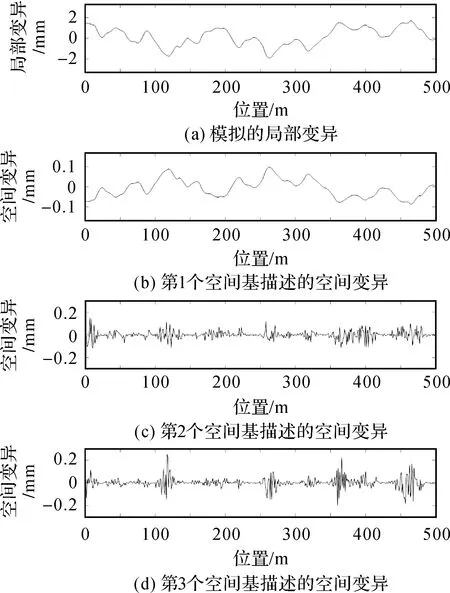
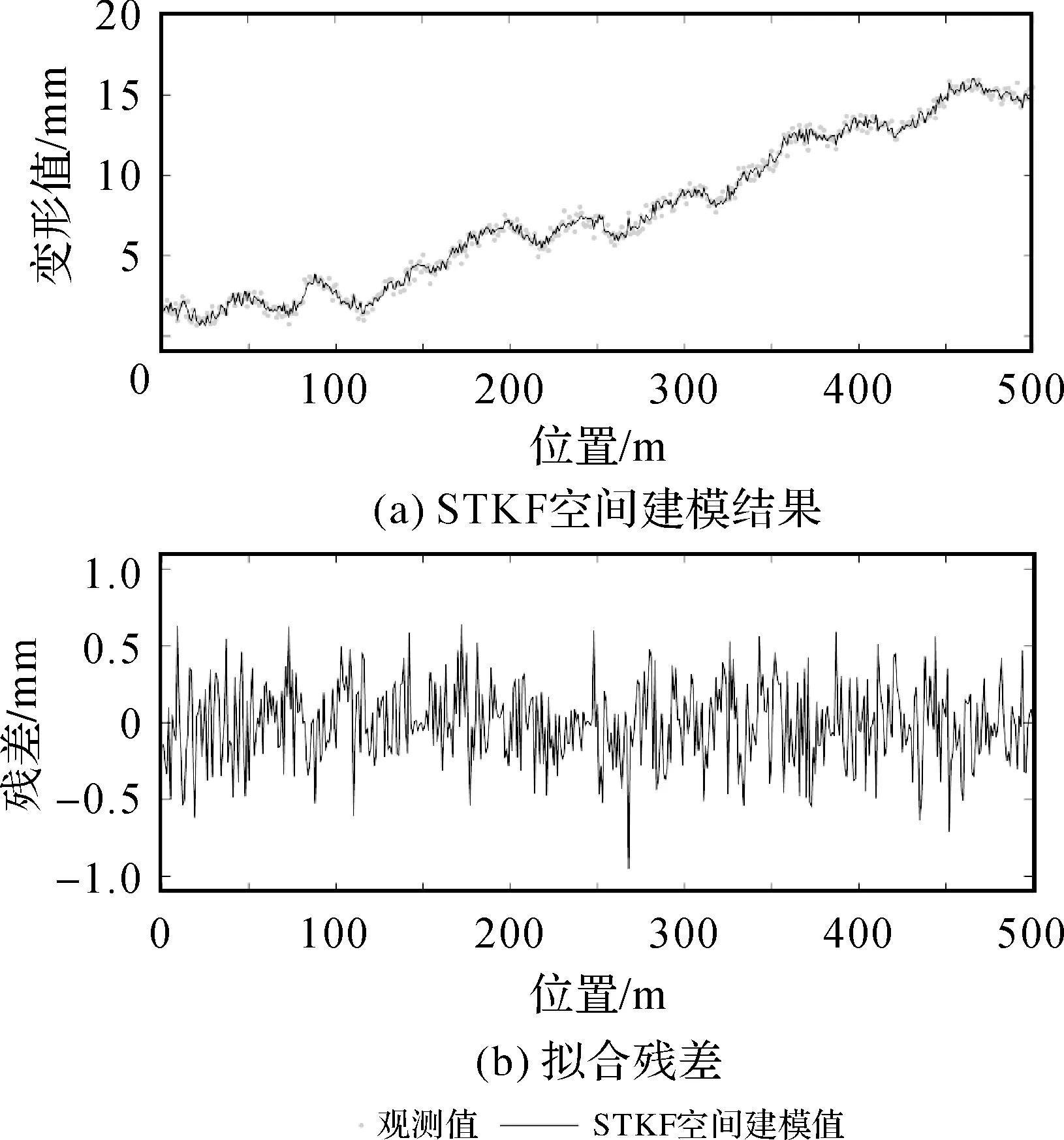
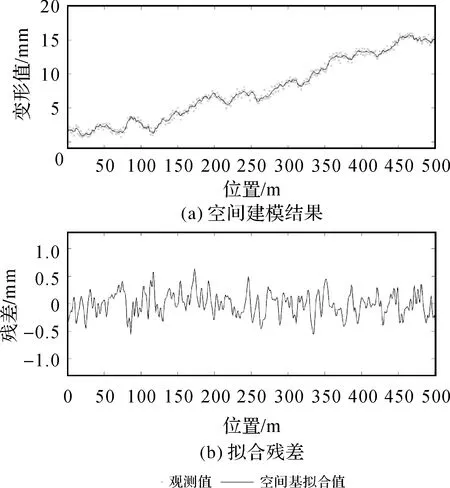
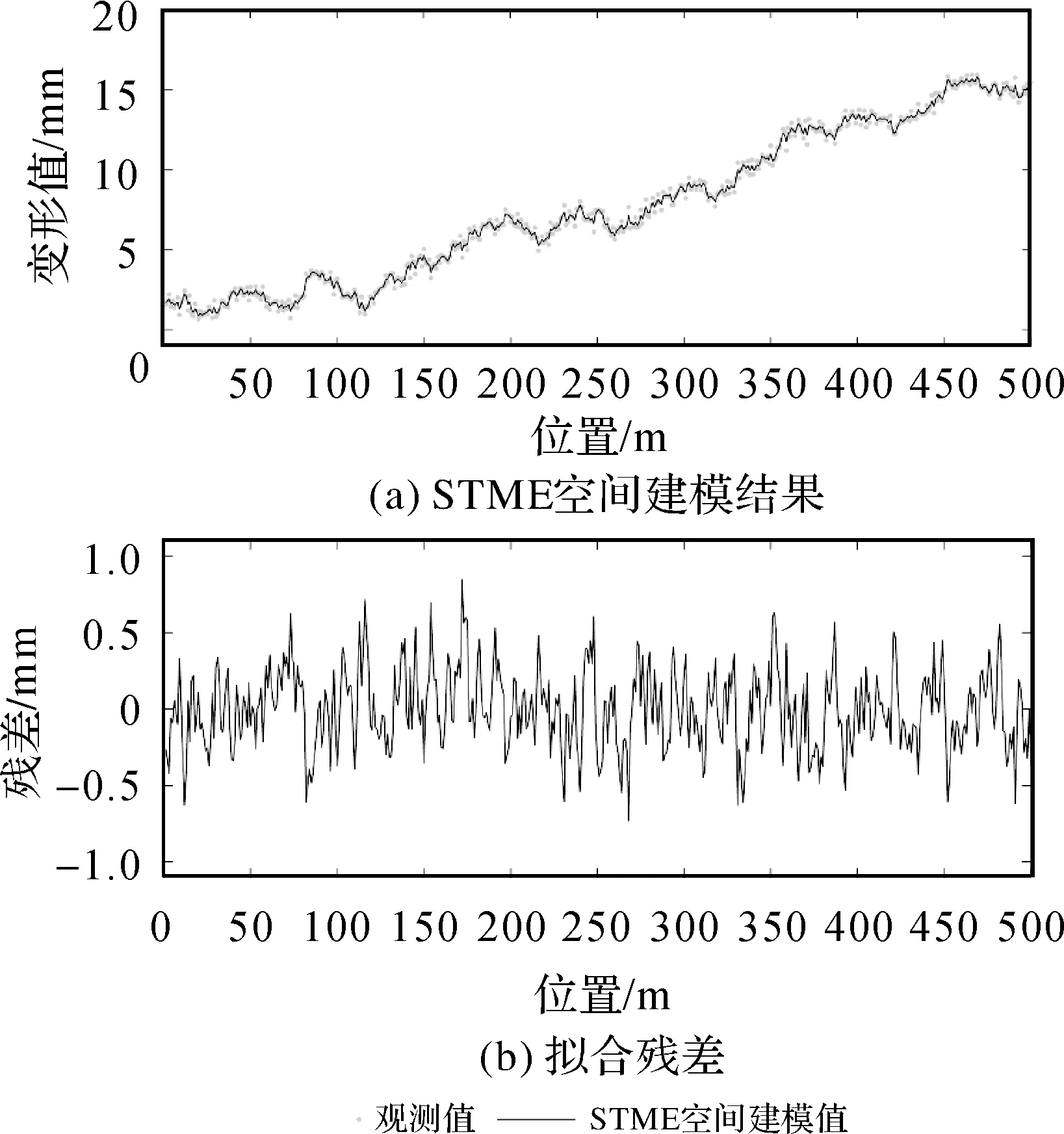
3 3种模型用于时空变形分析的试验分析
3.1 模拟试验
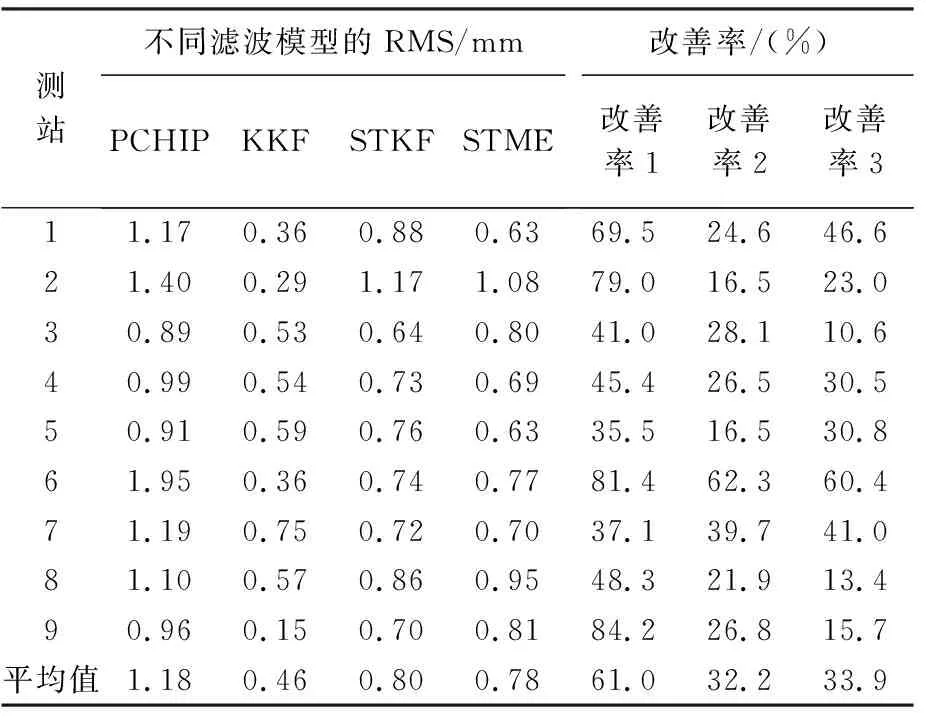
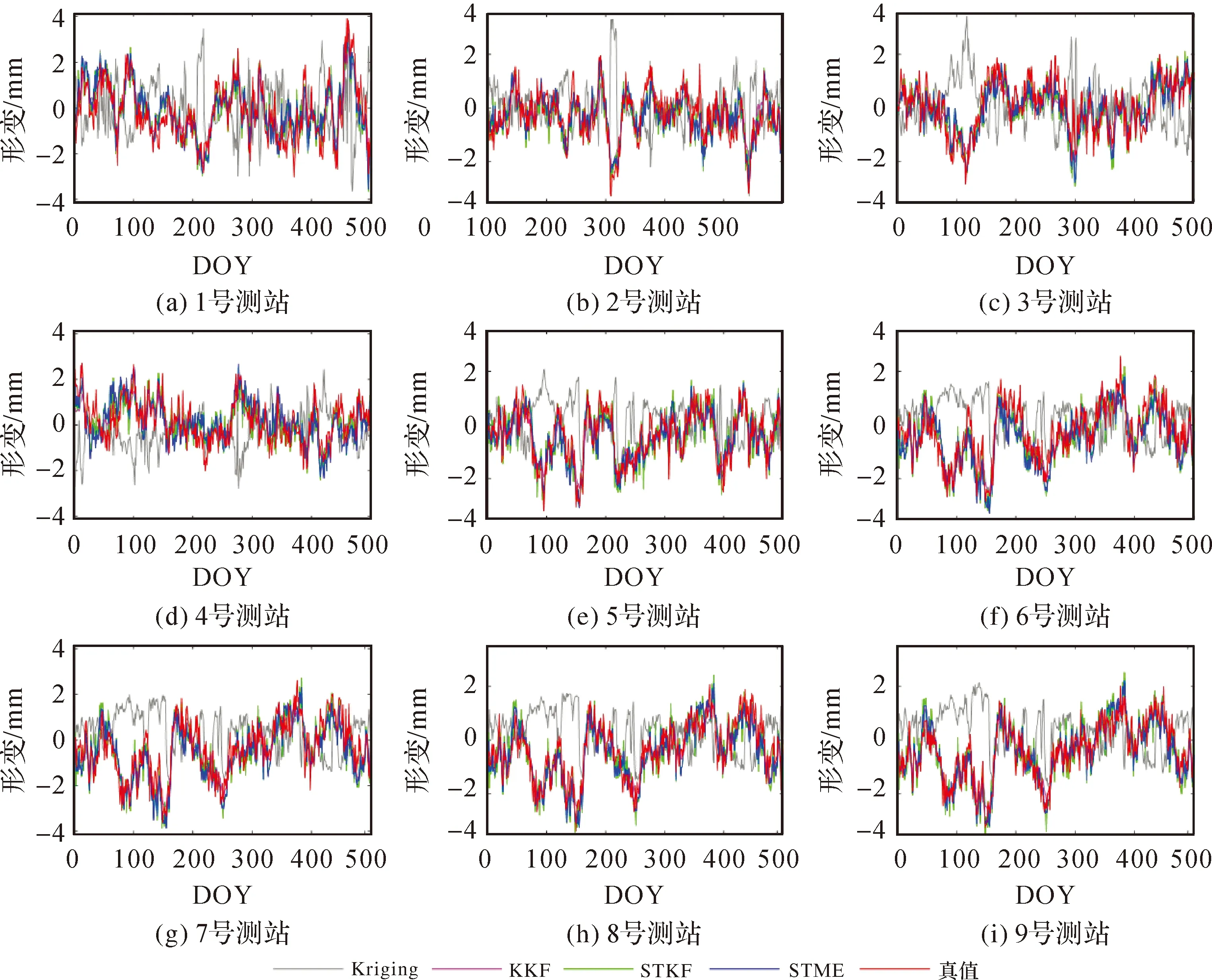
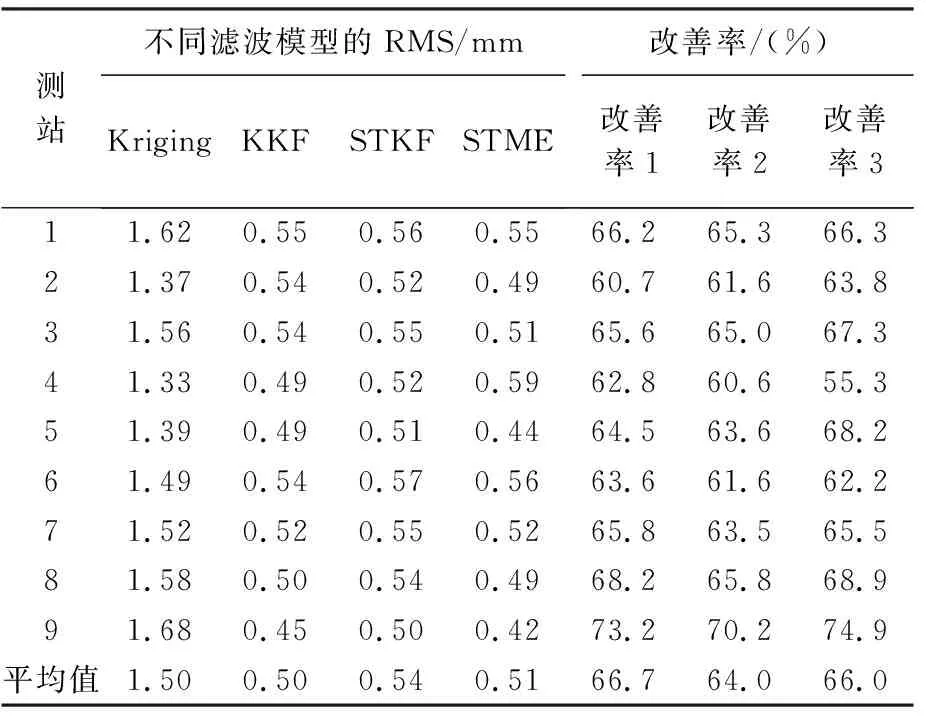
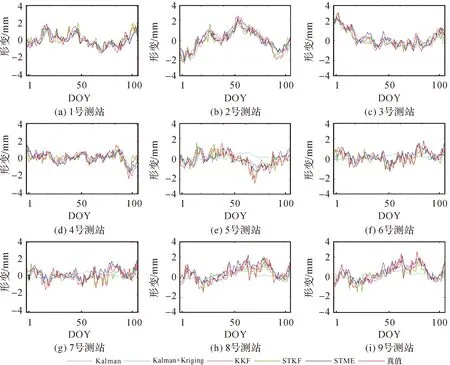
3.2 南加州地区GPS地面沉降数据试验
4 结 论
