航空液压系统流量智能预测方法研究

刘涌泉， 李巍*， 牛伟， 罗旭东

(1.中国航空工业集团有限公司第一飞机设计研究院， 西安 710089； 2.中国航空工业集团有限公司航空计算技术研究所， 西安 710068)

液压系统是飞机重要机载系统之一，它为飞机输出能源驱动，其性能、稳定性和可靠性直接影响飞机的安全性。流量是飞机液压系统的重要参数，实时监测液压系统管路流量可对系统特性分析、故障诊断提供有力的支持。在地面平台或大型地面工业系统中通常使用流量传感器测量管路流量，常见的流量传感器有涡轮式和齿轮式。但由于流量传感器需要串接在系统管路中，其造成的流阻对系统特性有显著影响，而航空液压系统对管路要求更为严格，因此目前在航空液压系统中鲜有应用。缺少流量参数的实时监测，将严重影响航空液压系统的故障诊断水平，因而对飞行保障能力带来巨大考验[1]。

针对液压系统的健康管理技术，近年来呈现出诊断对象多样化、诊断技术多元化、故障诊断与预测实时性、诊断预测与维护一体化、诊断系统的网格化、诊断信息的信息化和综合保障评价一体化的发展趋势[2-3]，目前液压系统的故障预测与健康管理(prognostics and health management，PHM)使用机载电子设备和飞机状态监控采集记录飞机的各项数据并进行转化筛选，提取故障数据格式化，形成不同等级的故障告警信息，辅助地面维修人员进行故障诊断，而对流量进行准确测量可以有效增加故障原始数据种类，从而对液压系统故障定位及后期维修带来便利[4]。

目前机上传感器配置条件下的流量难以监测，使用物理模型计算流量时由于实际管路具有大量耦合参数和时变参数，且管路雷诺数处于动态变化中，计算流量时会带来较大误差，而对于某个确定的管路段，其管路流量与管路两端的压差及管内温度理论上具有确定的函数关系，因此可以根据PHM思想，利用现有传感器数据进行重构，获取流量值。通过机器学习模型拟合构建输入输出间的复杂关系进行流量预测[5]。流量预测可以为飞机故障预测与健康管理服务，预测的结果合理准确，速度满足实时性需求，配合系统其余参数，就能够轻易地反映出系统工作状态，为飞行安全提供保障，提升系统PHM能力。

相比于传统的物理模型与概念模型，机器学习模型更加善于挖掘系统与数据间的隐形关联，更能抓住微妙变化，理论上只要拥有足够的训练样本，即样本空间无限大，机器学习模型所模拟的流量关系就更加接近现实的全部可能集合，但其中的隐性关系属于可观测但不可解释形式，阻碍了流量预测模型预测结果的应用，将物理模型与概念模型的成因机理与机器学习预测模型融合，可以提高模型适应变化的能力、增强模型解析透明度[6]。

GBRT算法作为一种重要的分类预测方法，其模型配置简单，对噪声数据有很好的适应性且模型解释性强，通过对近几年相关文献的研究发现，部分学者逐渐将此类方法应用于对交通车流量预测、旅游人流量预测及机组能耗预测等领域，都取得了较好的预测结果[7-8]。为此，针对变化工况下的飞机液压系统流量预测问题，建立了流量相关驱动因子挖掘方法，提出、构建并实现了基于梯度提升回归树(gradient boosting regression tree，GBRT)算法的流量预测模型，使用已有数据利用智能算法进行数据挖掘重构预测流量，为后续液压系统、机电系统的故障预测与健康管理水平提升提供了支持。

1 梯度提升回归树算法

1.1 集成学习方法

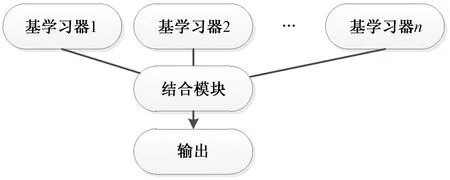
图1 集成学习方法Fig.1 Integrated learning method

集成学习方法(图1)是Dasarathy等[9]于1979年首次提出的一种处理决策问题的思路，集成学习是整合了多个以基础算法为核心的基学习器的强学习器算法，通过集成整合对训练样本进行更加准确的分类预测。

目前，以决策树为基学习器的分类方法主要分为Bagging方法和Boosting方法：Bagging算法(装袋算法)是一种团体学习框架方法，特点在于随机有放回采样，可以降低结果方差，避免过拟合，提升准确率与稳定性；Boosting算法是一种线性方法，通过对基学习器的加权组合，得到最终聚合模型，提高预测准确性。

1.2 回归树

GBRT模型是一种在Boosting算法基础上进行改进的算法，同样是以多个基学习器开展弱训练，其基学习器的核心是回归树算法[10]。回归树即使用树结构的模型进行回归问题求解，将样本空间进行每次一分为二的划分，划分为有限个区域，当决策时根据输入样本的特征进行划分，直到样本落入有限个区域中的一个，获得输入样本对应的预测结果。

1.3 梯度提升回归树

GBRT是Friedman[11]于2000年提出的一种机器学习Boosting方法，核心思想是将弱学习器学习结果的残差作为下个学习器的训练任务，沿损失函数负梯度方向训练，多次迭代后将各个弱学习器的学习结果进行线性累加形成强学习器的过程。每棵树对部分数据做好预测，后生成的树纠正前一棵树的错误，随着树的数量越来越多，不断提高迭代性能。

GBRT算法主要实现过程为：输入量为训练数据集D={(x1,y1),(x2,y2),…,(xN,yN)}和损失函数L[y,f(x)]，输出为回归树H(x)，其中，(xi，yi)为系统输入与系统输出，i=1，2，…，N，f(x)为预测输出值。

首先进行初始化，将首预测值f0(x)定义为

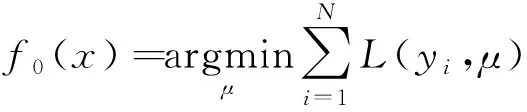
(1)

式(1)中：μ为使损失函数极小化的常数值，描述在空间内是一个只含有根节点无分支的树。

对于所有的样本N，fori=1 toN，其中i为第i个样本，假设迭代次数为M，m为第m棵树，计算当前损失函数的负梯度值，并将它作为与实际值的残差的估计值rim,可表示为

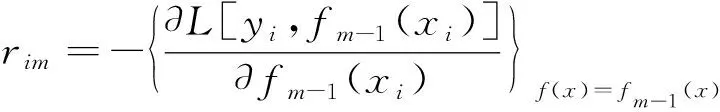
(2)

式(2)中：fm-1为第m-1棵故障树模型。

针对残差生成回归树Hm(x)，计算梯度下降的步长ρm，其计算公式为

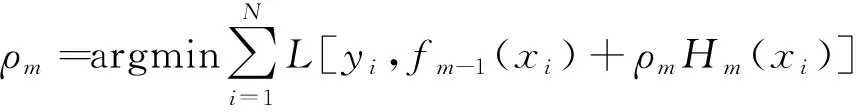
(3)

不断迭代后最终生成的模型为

fm(x)=fm-1(x)+ρmHm(x)

(4)

根据生成的每棵树模型分配权重，渐进逼近最佳模型为

fm(x)=fm-1(x)+lrρmHm(x)

(5)

式(5)中：lr为学习率，即对每个基学习器分配的权重缩减系数。

设置学习率可以避免模型过拟合，提高模型泛化能力，同时GBRT算法的精度还与回归树复杂程度，即树的数量相关。

2 流量建模探究

2.1 液压系统流量

液压系统油液在管道中流动，油液与管壁的摩擦、管道截面积的变化、油液流向的变化等，都会导致管路中油液压力的损失。

单管路中的压力损失ΔPtotal包含沿程压力损失ΔPalong和局部压力损失ΔPpart，其相应的理论计算公式分别为

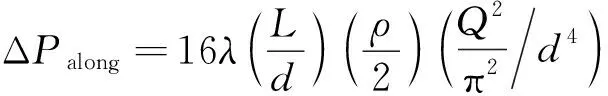
(6)

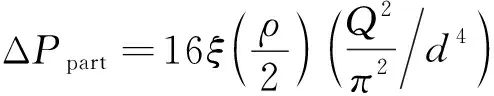
(7)

式中：L为导管长度，m；d为导管内径，m；ρ为油液密度，kg/m3；Q为油液流量，m3/s；λ为沿程阻力系数；ξ为局部阻力系数。

针对单一管路，有一系列局部损失，并且又由不同管径的管串联起来，其总阻力损失等于沿程损失与局部损失之和的叠加，即

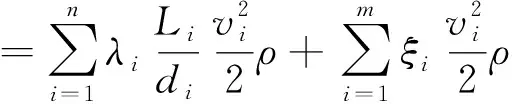
=KQ2

(8)

式(8)中：Δp为压力损失，Pa；K为管路流量模数，N·s2/m8；λi为第i段管路的沿程阻力系数；Li为第i段导管长度；di为第i段导管内径；Fi为管路内截面积，m3；vi为平均流速，m/s。

管路模数K与液压油种类、管材、管径、管路走向、液压附件等均有关联，而当管路各项参数均确定的情况下，可通过管路流阻反推管路流量，即

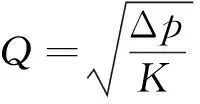
(9)

但由于管路的雷诺数一直处于动态变化的过程中，进而动态影响K值的相关参量：沿程阻力系数与局部阻力系数；同时在温度的影响下，管路内流体的黏度也在持续变化中，因此管路流量的逆推导求解变得极其困难。而使用GBRT方法，可以将整个系统考虑为动态变化的黑箱模型，构建多输入(压力、温度、压差等参数)单输出(流量)关系，通过数据驱动的方式拟合预测流量值。模型训练与预测过程如图2所示。

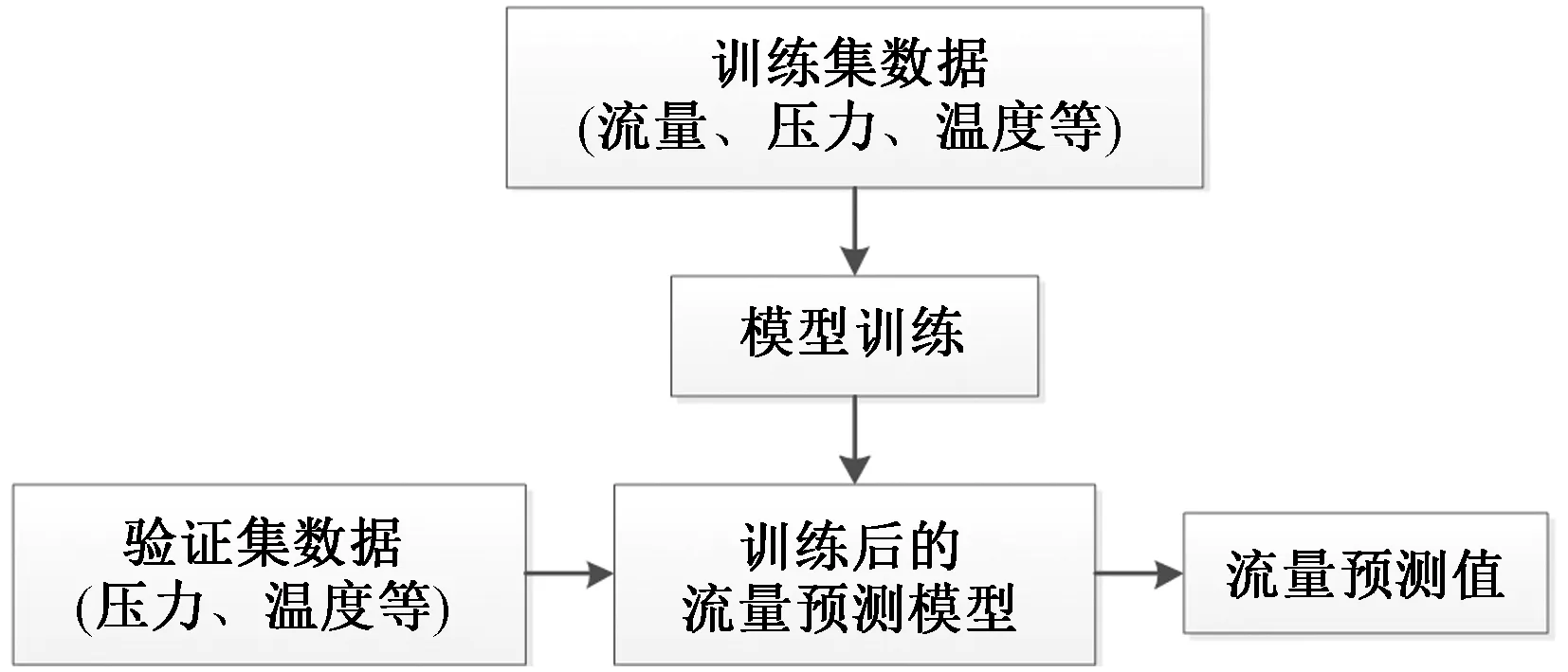
图2 模型训练与预测过程Fig.2 Model training and prediction process

2.2 模型建立流程

以梯度提升回归树算法建立液压系统管路流量预测模型，建模过程包括数据预处理，特征选择，模型训练评估决策，建模流程如图3所示，具体步骤如下。

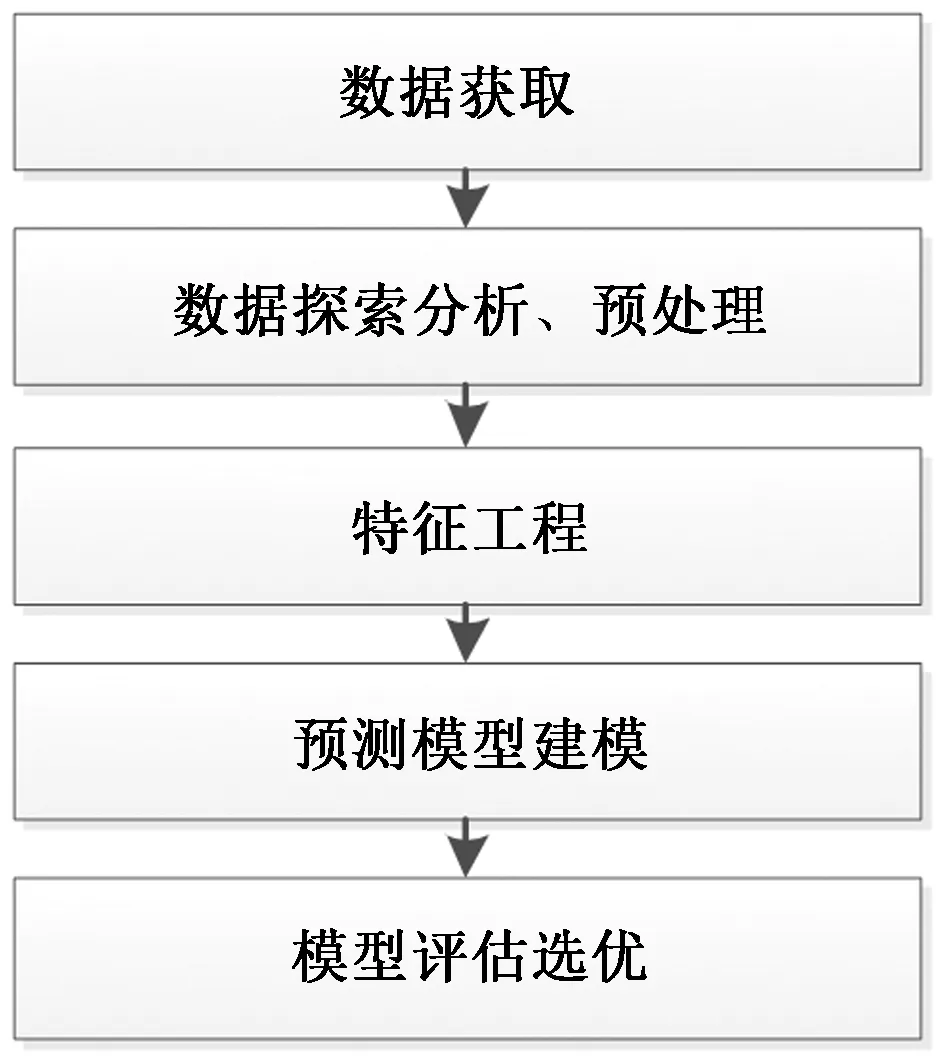
图3 流量预测模型建模流程图Fig.3 Flow prediction model modeling flow chart

步骤1按照机上管路布置状况搭建液压试验平台并加装参数测量传感器，同时根据监督学习思想加装流量传感器，使其测量值作为训练标签值，获取模型训练所需数据集合。

步骤2将测得的数据进行探索分析、预处理。

步骤3特征工程，筛选出与流量预测强相关的参数集合，剔除流量的弱相关参数。

步骤4选取多种机器学习监督学习算法建立流量预测的数据驱动模型。

步骤5对模型评估选优，选取对流量预测结果准确率较高的算法。

2.3 数据获取

通过对流量的相关参量进行研究，并以此为基础进行试验设计[12-13]。以实际管路分布状态为标准，进行系统试验台架搭建，并在不同位置加装温度、压力、流量传感器，考虑到流量传感器带来的较大流阻，选择在各支路供压端、回油端和总回路汇流端加装流量传感器，减少对系统正常功能带来的影响的同时获取流量数据，试验结构示意图如图4所示。

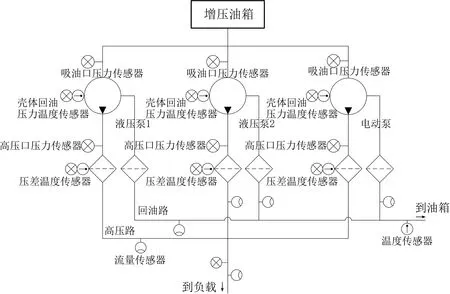
图4 液压系统试验结构示意图Fig.4 Schematic diagram of hydraulic system test structure

在各泵吸油口与壳体回油口安装压力、流量、温度传感器，对系统加装负载模拟组件，限定某飞行任务工况下调节负载，模拟实际过程的供压、流量、温度等参数变化情况[11]，对管路中动态变化的主要参数进行连续测量，主要测量参数类型如表1所示。

通过调整负载模拟系统流量，单开、多开液压泵分类进行系统参数测量，得到包含上述变量的共计7种不同工况下的31类数据。

2.4 数据预处理

针对数据采集中出现的缺失值与异常值进行预处理可以有效提升分析结果准确性，由于本试验数据来自系统试验台传感器的连续采样[14-15]，各个工况下的待求负载模拟流量的范围、变化趋势都有很大的差别，试验选取的不同工况的负载流量曲线，如图5所示。

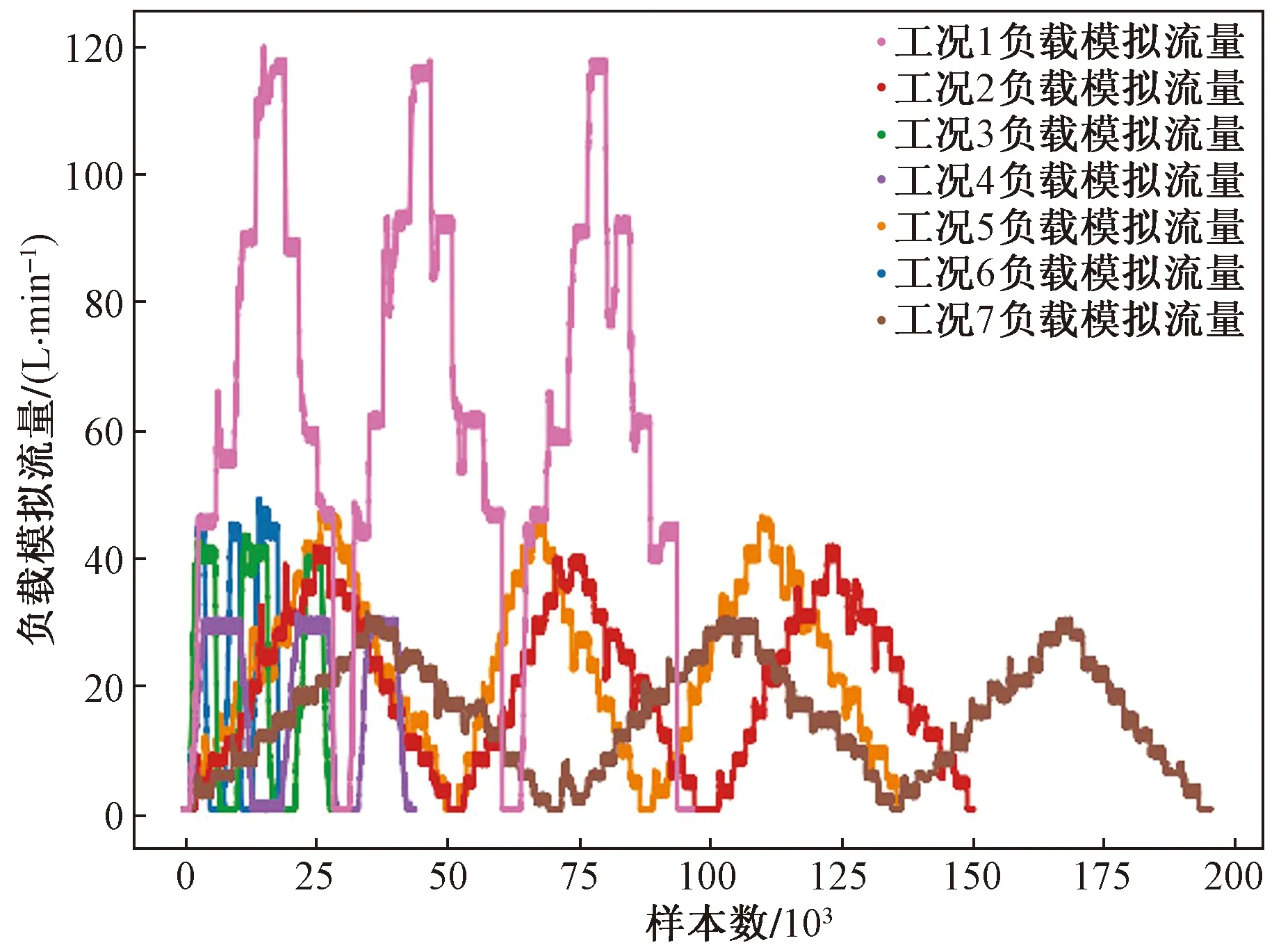
图5 不同工况下负载模拟流量变化曲线Fig.5 Load simulation flow curve under different working conditions

因此选择将不同工况下的数据集整合为一个大数据集，即采用类似数据扩增的方法，可以有效提高特征维度，减少模型训练次数提升效率，同时尽量避免模型训练结果的过拟合问题。最终得到数据规模(672 181，32)，31个传感器特征加1个时间特征。

2.5 特征工程

对采集到的全部参数进行Pearson相关性分析并生成热力图，相关性分析结果如图6所示。

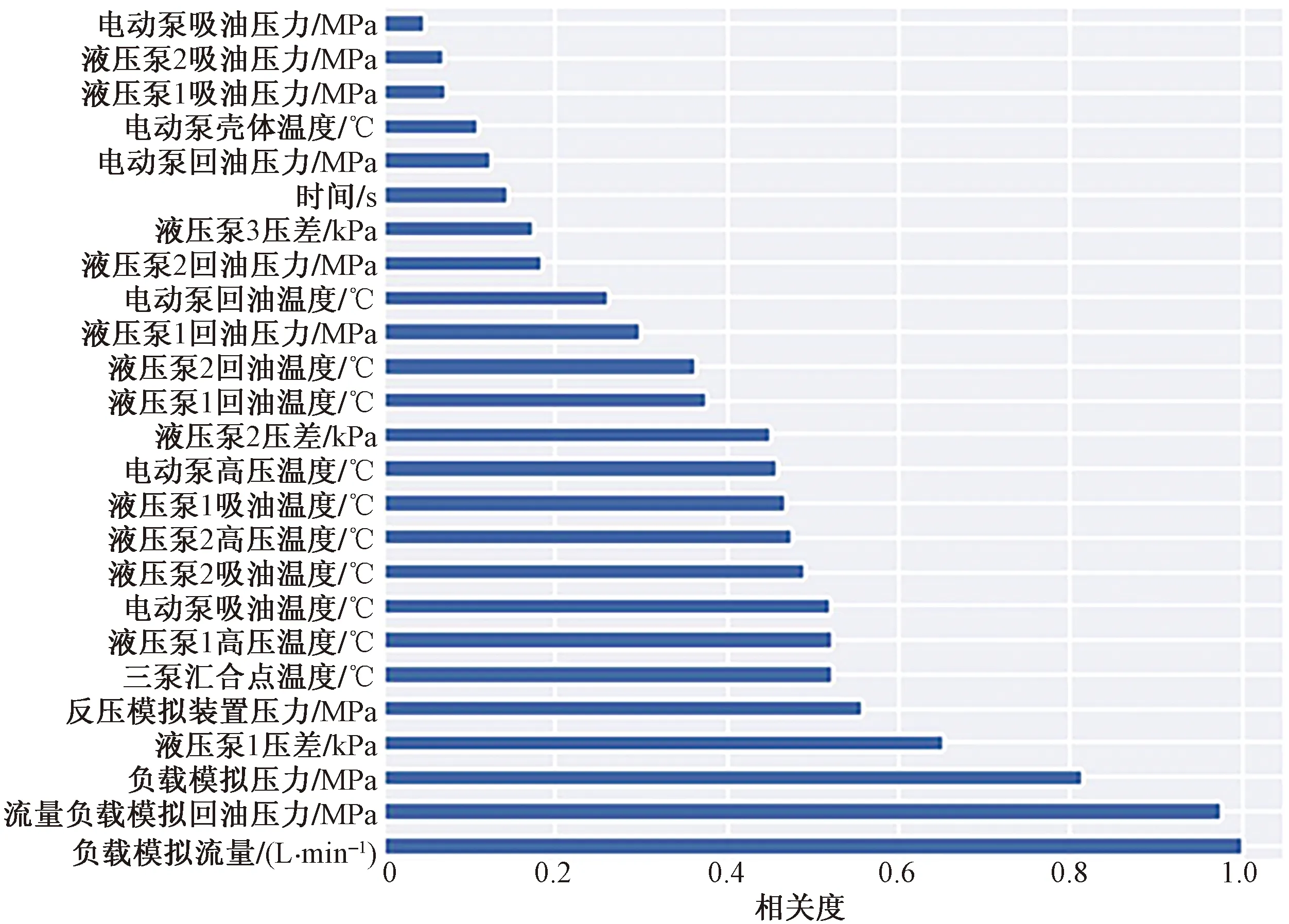
图6 Pearson相关系数值图Fig.6 Absolute value of Pearson correlation coefficient

从图6可以看出，多个特征之间的相关性较强，需要根据情况进行特征选择，避免多重共线性。考虑到负载模拟压力、反压模拟装置压力、流量负载模拟回油压力与待求负载模拟流量的强相关性，选择的每种方法均训练两种模型：Model-t模型接受这3个参数作为模型输入，Model-3模型不接受其作为模型输入，以应对未来运用中工况，参数条件变化后的预测要求。

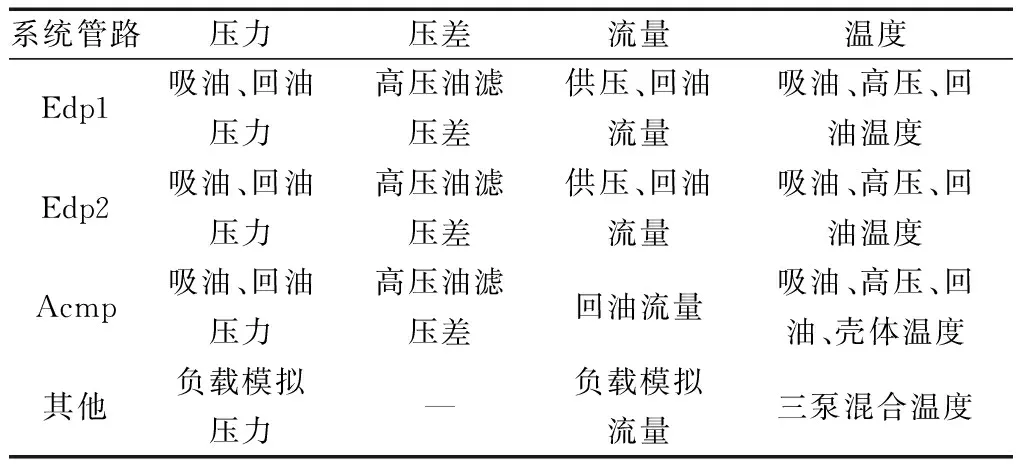
表1 系统管路测量参数类型

3 试验对比研究

试验采用液压试验台采集的数据集对模型进行训练，调整输入特征种类以获取最佳组合，并使用测试数据集对模型进行验证。将实际与预测值的差值转换成回归评价指标，对模型以及模型属性进行分析。

3.1 试验数据划分与评价指标

试验中使用交叉验证的方法对原始样本进行随机拆分数据集，其中67%的数据作为训练数据，33%的数据作为测试数据。

本试验使用的回归评价指标包括:平均绝对误差(mean absolute error，MAE)、均方根误差(root mean square error，RMSE)、拟合优度决定系数R2，以及训练时间与测试时间。计算公式分别为

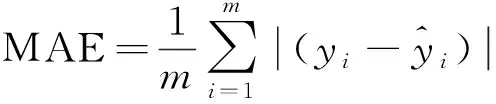
(10)

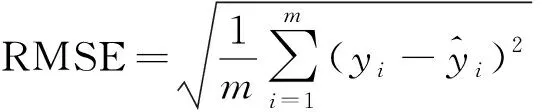
(11)

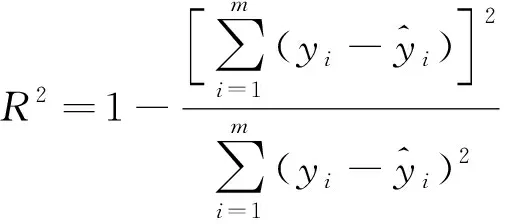
(12)

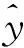
3.2 试验结果对比

将所建立的模型与最小二乘线性回归模型、树模型、极端提升树等模型的预测精度进行对比，以验证其在液压系统流量预测方面有效性[16-17]。对每种模型分别建立Model-t与Model-3两种训练输入条件，并验证预测准确性，以蓝色为真实值，红色为预测值分别绘制训练结果图。

最小二乘回归模型预测结果如图7、图8所示，可以看出，接受3个强相关参数为模型训练输入条件的Model-t模型对流量的预测结果明显好于去掉强相关参数作为输入的Model-3模型。使用回归评价指标对模型结果进行评估，表2为最小二乘回归预测结果。

决策树回归预测结果如图9、图10所示。决策树回归预测指标如表3所示。GBRT模型预测结果如图11、图12所示。梯度提升回归树模型预测指标如表4所示。对比传统最小二乘回归、决策树与GBRT三类模型可知，相较于传统数学方法、机器学习流量模型在预测精度上更有优势，但需要更长的训练时间，但在不包含强相关参数的输入条件下具有更好的预测效果。选取算法更为复杂的极端梯度提升树(XGBoot)模型作为对照，训练结果如图13、图14所示。极端梯度提升树模型预测指标如表5所示。

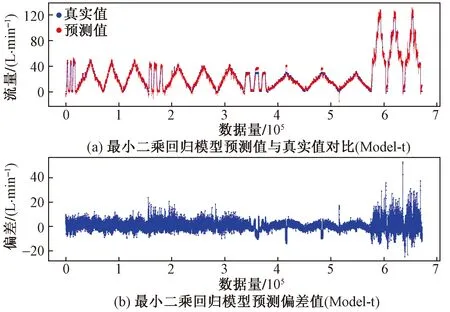
图7 最小二乘回归预测结果(Model-t)Fig.7 Least square regression prediction results (Model-t)

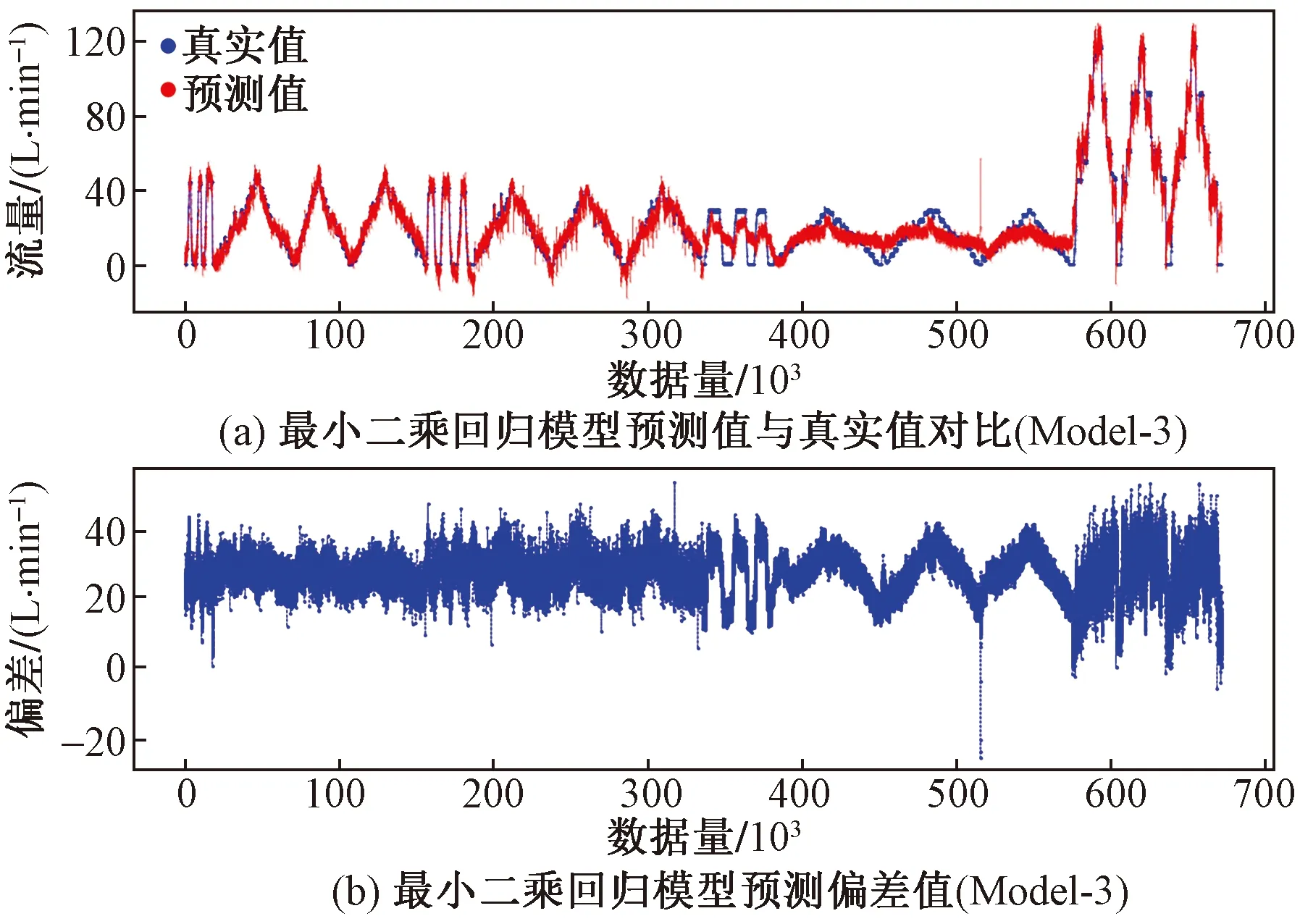
图8 最小二乘回归预测结果(Model-3)Fig.8 Least square regression prediction results (Model-3)

表2 最小二乘回归预测结果

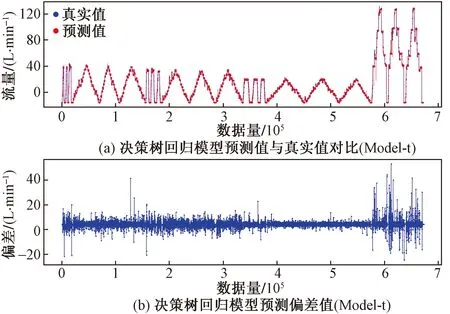
图9 决策树回归预测结果(Model-t)Fig.9 Decision tree regression prediction results(Model-t)

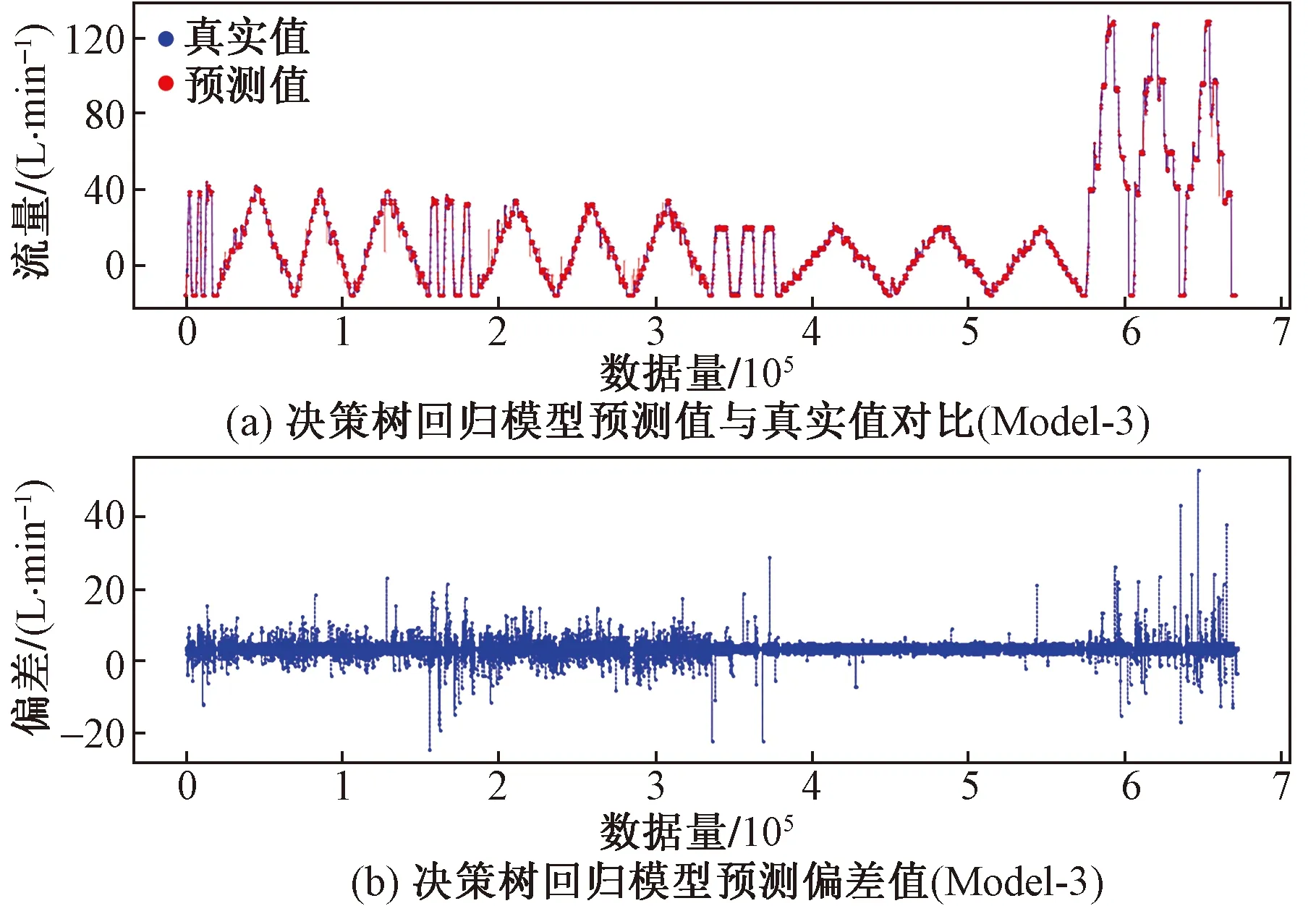
图10 决策树回归预测结果(Model-3)Fig.10 Decision tree regression prediction results (Model-3)

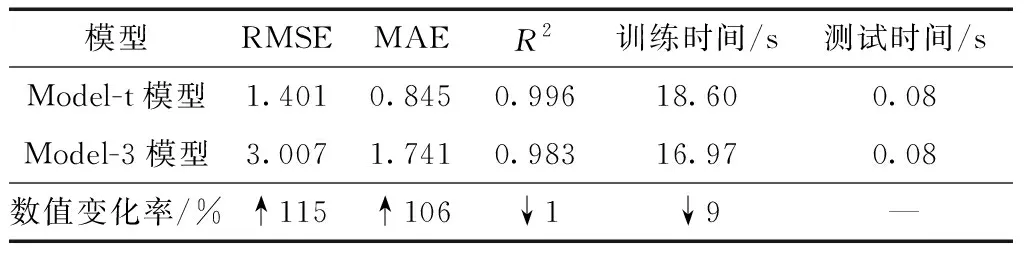
表3 决策树回归预测结果

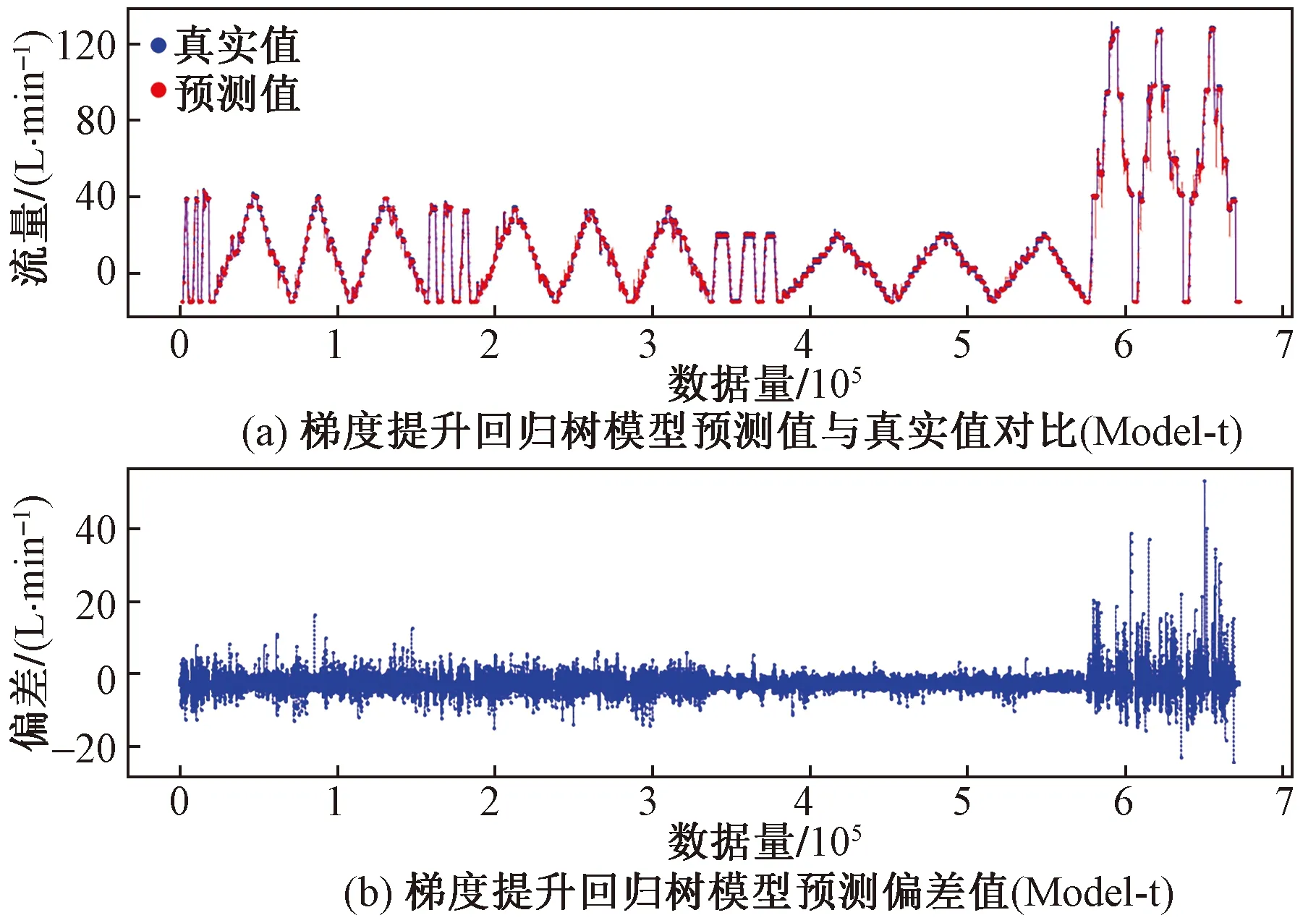
图11 GBRT预测结果(Model-t)Fig.11 GBRT prediction results (Model-t)

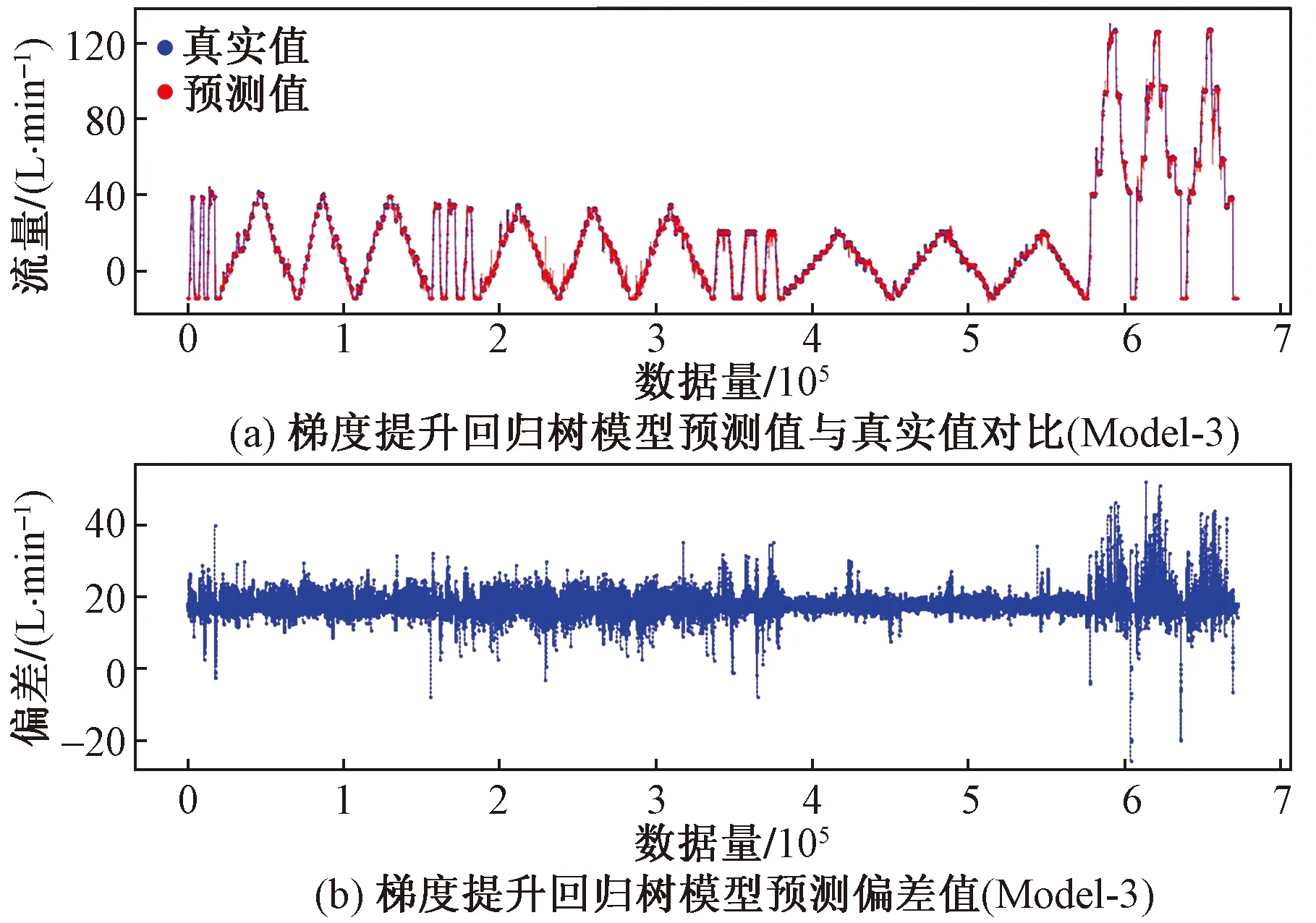
图12 梯度提升回归树GBRT预测结果(Model-3)Fig.12 Gradient lifting regression tree GBRT prediction results (Model-3)

Model-t与Model-3不同回归算法预测模型的结果精度对比如表6、表7所示。

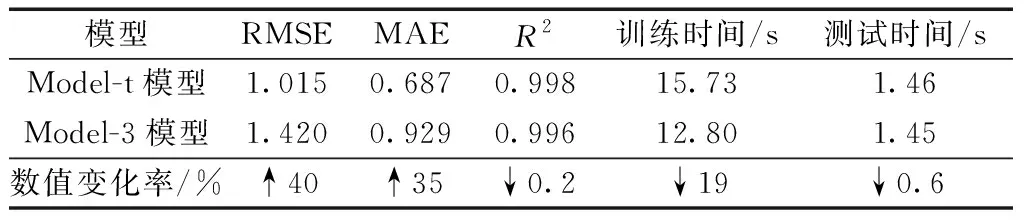
表4 GBRT预测结果

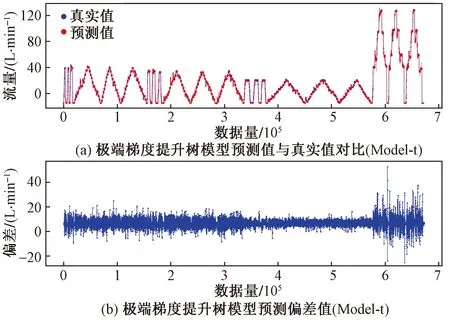
XGBoot为极端梯度提升树图13 XGBoost预测结果(Model-t)Fig.13 Prediction results of XGBoost (Model-t)

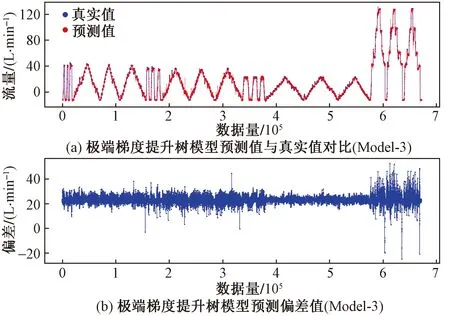
图14 XGBoost预测结果(Model-3)Fig.14 Prediction results of XGBoost (Model-3)

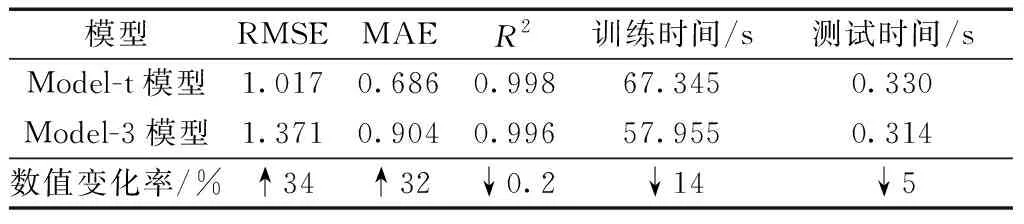
表5 XGBoost预测结果

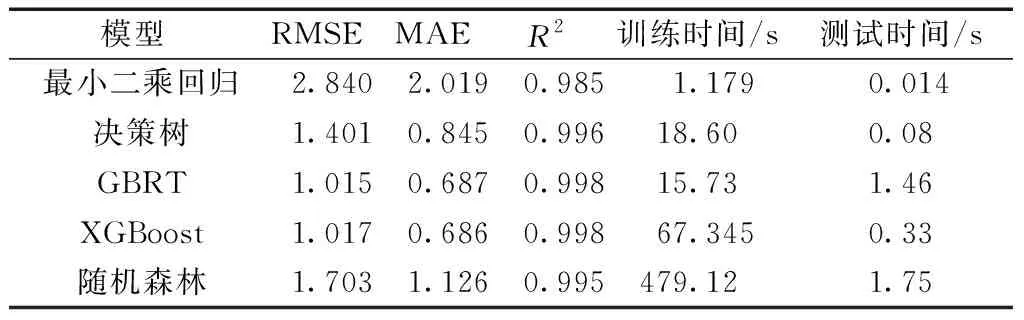
表6 Model-t不同回归算法预测结果精度对比

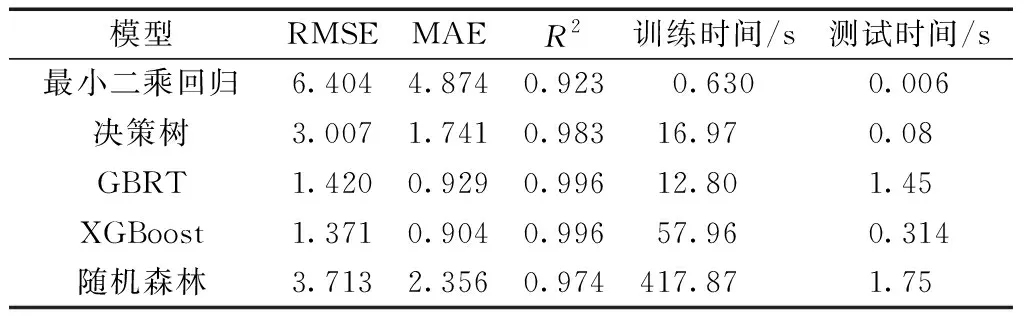
表7 Model-3不同回归算法预测结果精度对比

通过分析结果可知，最小二乘线性回归方法预测准确度相对较差，但在可接受范围内，其模型训练时间明显小于其他方法；决策树，GBRT算法具有较高的模型精度，同时相比于极端梯度提升树具有较短的模型运行时间；随机森林与其他机器学习方法相比，模型精度没有优势，且训练时间过长。去除与负载模拟流量强相关的3个特征后，几乎所有模型的准确度均有所降低，最小二乘线性回归方法的预测误差相对较大，但模型训练时间最短；随机森林与其他机器学习方法相比，模型精度没有优势，且训练时间过长。同时考虑预测精度与训练时间，最优模型为GBRT，五类算法的模型测试时间均较短。

4 结论

(1)相较于传统的数据预测算法，提出的机理与智能数据挖掘算法结合的系统流量预测模型具有较高的准确性，能够根据目前机上已部署的传感设备，对无法测量的状态量进行准确的估计预测，符合预期效果。

(2)基于液压系统流量机理及成因规律，开展流量预测机器学习模型构建、地面液压试验平台搭建、实例验证与对比评价研究。基于选取的机器学习中的监督学习算法，结合飞机液压系统流量产生机理与相关参数关联关系，建立了基于液压试验平台的预测算法验证框架，对该框架进行不同模型间的实例验证与对比评价，为后续研究工作提出一种新的思路。