基于利用牛顿环实验数据修正的教学讨论

浦文婧，黄玲玲，史 博，程德胜，张 辉，温佳起

(中国人民解放军陆军炮兵防空兵学院，安徽 合肥 230000)

牛顿环仪是一种常见的观察光的干涉的光学器件，可以观察到光的等厚干涉[1]，帮助学生加深对光的干涉属性的理解；学习精确地测定光学元器件的特性参数，如单色光的波长[2]、液体折射率[3,4]平凸透镜的曲率半径[5]等。因此牛顿环是大学物理实验中的基础必做实验之一。

1 教学实施过程

其次，针对初次进入实验室的学生，测量经验基本相同，经常出现操作错误的地方(如：目镜对焦不清晰引入视差，圆环的计数存在偏差，不按照操作规程引入空程误差，不估读导致的计数错误，以及读数量过大使读数错误率增加等。)应着重强调。这样可以尽可能使测量新手处于同一测量水平，实验中尽量选择同一批次牛顿环进行测量，学生实际测量结果横向对比分析具有客观性。

最后，在测量完毕后引导和带领学生共同分析实验数据，横纵向对比。(1)利用学生偏好横向对比的心理，发现组与组间的数据偏差，求证测量误差的来源；(2)引导学生改进数据处理方法，在数据处理的过程中研判数据处理方法的合理性和针对性，推测系统误差的主要来源。(3)带领学生横纵向对比，探究误差主要影响因素，提出修正方案。(4)修正实验数据，形成科学研究的闭环，升华物理实验思想。

整个教学过程中，数据处理成为了实验的重难点部分，课时比重增高，引导启发增多。这样会更有利于培养学生严谨的科学作风，客观的科学眼光，求是的科学态度。真正意义上利用实验课程培养学生的科学思维，提高理论联系实际的实践技能。

2 实施过程与结果

表1为某次实验随机10组学生的测量数据。

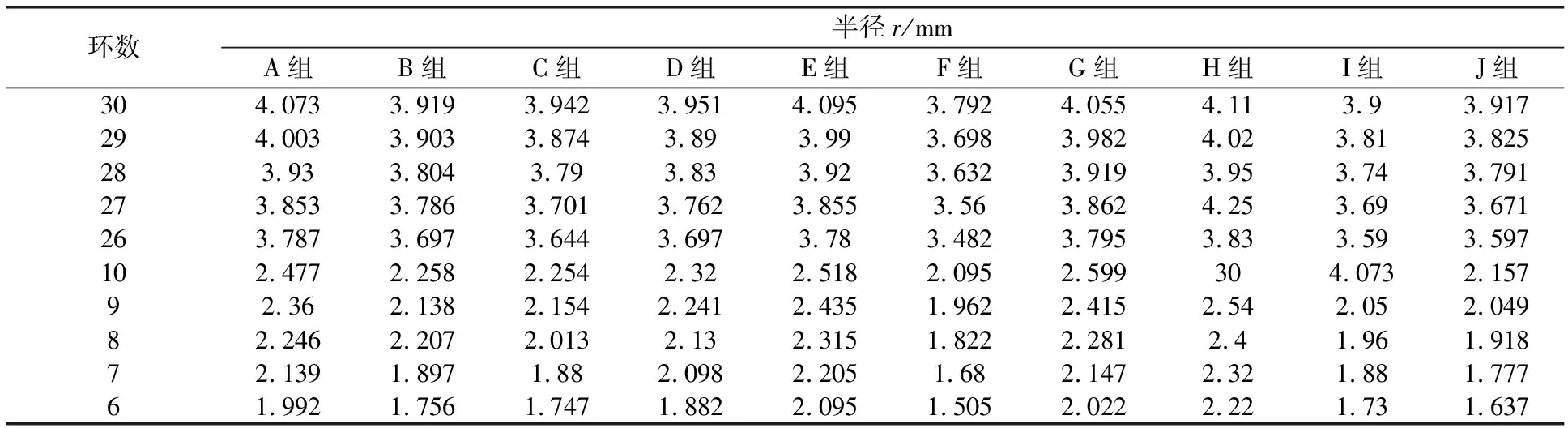
表1 某次实验中随机的10组学生测量数据

(1)利用学生偏好横向对比的心理，发现组与组间的数据偏差，求证测量误差的来源。

每组学生先将各自的测量值带入公式，得到曲率半径的实测值，交给老师。老师通过学生数据绘制出各级环对应的曲率半径R，得到图1的规律。

环数

从图1可以看出，大部分学生都测出了曲率半径随环数增加而发生变化的规律。曲率半径是材料的本征属性，应为定值，得到这样的数据显然不尽合理，在教学过程中可以引导学生探讨误差来源和数据的可靠性。

学生的惯用思维是直接将各组测得的曲率半径相加求平均，会得到图2规律，说明学生并不理解该种方法的局限性。

组别

实际上，数据间彼此平行度差，求取平均虽然可以使测量数据均一化，但不利于发现数据的整体规律；在所用仪器相同的情况下，数据不同，学生也首先分析是测量不仔细造成的，但多组比较能更准确的揭示深层原因。因此，需要进一步引导学生思考如何选择数据处理方法。

分析两图可以发现，实测的曲率半径是变化的，这与曲率半径为定值的理论相矛盾。各组在环数较小时，测量值R的变化率较大，波动明显，环数大时R的变化率减小，波动趋于平稳，且所有组数据都在800～1 000之间。这些说明环数m小时，数据测量的误差较大，且每组都体现了这样的趋势，是实验共性。因此，就需要追究测量误差的来源及消除误差的方法。

(2)引导学生改进数据处理方法，在数据处理的过程中研判数据处理方法的合理性和针对性，进而推测引入系统误差的主要因素。

要求学生用逐差法处理数据后，得到的规律与直接求均值相比，教师作对比图如图3所示。显然，逐差法处理后的各组的测量均值处在了同一水平。理论上，逐差法也相当于消除了绝对级次不准确的因素，用相对环差来求取R；这种数据处理的方法大大增加了学生对数据和测量方法的肯定，也对逐差法消除系统误差的意义有了深入理解。

组别

如此，各组间得到了组间较为接近的数据，但组间差距仍然存在。引导学生分辨诸如视力差异、耐心程度、中心暗斑大小等影响实际因素的影响力并讨论，大部分学生都凭直觉认为暗斑大小是影响数据结果的主要因素，暗斑的大小可以调节么，具体是多少，影响有多大呢？

(3)带领学生横纵向对比，探究误差主要影响因素，提出修正方案。

要确定暗斑的影响，就必须计算出每组牛顿环暗斑中包含的具体环数。

环数/m

表2 各组暗斑中的环数

将学生根据上式计算出中心暗斑环数列表如下，并将各组的暗环数目与逐差法得到的实测R值进行对比，如图5所示。由于所用的牛顿环平凸透镜曲率半径理论值约为860 mm，故将860 mm和0级环设为中心线，以便对比。结果显示，级数m′较小的几组中仅有一组R值与理论值接近，而在m′较大的几组中反而有三组R值与理论值接近。说明这些组间的误差来源属于随机误差，与中心暗斑的级数无直接关系。

组别

这组数据否定了学生推测的“暗斑大小是影响数据结果的主要因素”，再分析测量公式也不难看出，a与R是相互独立的分量，并无直接关系。这种深入的分析使学生认识到，不能仅依靠组间差异来判断实验的影响因素，更应该尊重客观数据处理的结果。学生提出“能否用暗斑环数修正曲率半径R，使数据都回归到理想的原点？”这也正是将要讨论的问题。

(4)修正实验结果，形成科学研究的闭环，升华物理实验思想。

前述数据整理得出两个结论：各组靠近中心暗斑处的测量误差偏大；中心暗斑的级数与测量准确性无必然联系。看似矛盾的结论，根源在于公式推导并非基于现实状态，如果用实测数据线性回归得到的暗斑环数修正数据，理论上也是重新寻找实验数据基准点的过程，是可行的。各组间的数据差别会缩小么？

将各组环数代入原始数据，增加或减少相应的环数，重新确定级数m，得到修正后级数m与R的关系，如图6所示。

修正后的环数m

由图中可以看出，这次得到的R数据趋于平均水平，修正后靠中心的环数据也回归到平均水平。说明中心暗斑在很大程度上影响了数据的偏差，对靠近中心的数据影响更大，但对线性规律的影响不大。在这里可以进一步深入分析原因，即靠近中心的凸透镜因接触压变而产生的形变量大，影响大；光线进入透镜再反射也会引起读数偏差，衍射环半径越小处，偏差会越大，因此如果选取大环测量，会大大降低读数误差。

这一步数据处理，帮助学生理解了从实测数据出发，找到数据规律后再对原始数据修正的过程，是对数据整理再加工的过程，在实际实验和寻找科学规律的过程中都十分必要，有助于更加准确的判断客观规律。

3 结 语

(1)实验中，即便学生的基础薄弱，也适用于用未修正的公式进行测量的教学方法，在逐步发现错误中修正错误，学习数据处理的思想和思路，获得实践检验真理的实验精髓。

(2)采用了未经修正的测量公式，也有近一半的学生得到了接近理论值的测量值，说明为了使测量更准确，公式修正可以放在初测之后，或由学生讨论得出。

(3)在教学中，应该对学生的基础有基本掌握后，再采用学为主体的教学方案，若实验侧重数据处理，将有助于提升学生科学实验思维和整体的实验素质。

数据处理的过程中，学生认识到必须明确数据间的联系和规律，而不能简单的求平均值；其次评估建模不准确带来的测量误差，并通过分析数据找到不准确的原因；随后结合理论和数据，深刻理解了归一化处理的意义；最后利用数据处理求出暗斑级数，再代回修正原始实验数据，大大加深了对误差因素、测量修正和数据处理意义的领悟。整个过程基于对实验数据的怀疑和修正，思路更清晰，接受度更高，可以进一步升华数据处理的实践指导和修正意义。

因此，这种教学改革强化了知识运用，强调以学为主体，采用引导教学，使学生在试错的过程中发现问题并解决问题，真正做到了实验思想的始末贯穿，能够收获更好的教学效果，值得尝试和推广。