基于物理的流固交互仿真方法综述

赵 静,许立群,安泳钢,王洪玉,唐 勇,*

(1.燕山大学 河北省计算机虚拟技术与系统集成重点实验室,河北 秦皇岛 066004;2.燕山大学 信息科学与工程学院,河北 秦皇岛 066004;3.东北大学秦皇岛分校,河北 秦皇岛 066004)

0 引言

在虚拟世界中模拟自然现象是计算机图形学中一个重要研究领域,而流固交互现象因其流体拓扑结构变化剧烈、非线性固体模型种类多样、流固接触面边界条件复杂以及整体方案需隐式求解等特点,使之成为图形学中最充满挑战的一个分支,这也吸引了国内外很多研究者对流固交互技术展开深入研究。目前流固交互技术已经广泛应用于力学分析、虚拟现实、游戏影视等领域。由于虚拟空间中的流体运动通过求解偏微分方程获得,固体的形变效果由其应力应变关系决定,因此目前研究者主要从流体和固体的表示方法和离散化方案、拓扑结构、边界条件以及加速策略等几个角度对流固交互过程中涉及的技术进行探索和研究。

如今,在基于物理的真实场景模拟中对流固交互技术的需求正越来越强烈,如模拟填充空气的橡胶轮胎、液压过程、空中飞行的飞机或者水中漂浮的船等。除了自然环境的真实感重现,在虚拟手术[1-2]、数字装配[3]以及软体机器人[4]等领域也都应用了大量的流固交互相关内容。

由于流固交互在实现过程中会使用到不同的表示方法,这使得同步处理交互过程中的边界条件充满挑战。最初,通常使用分区方案处理流固交互过程,即在流体和固体间单独地迭代计算,并使用其中一个材料的属性定义另一个材料的边界条件[5-6]。然而这种简单直接的计算方法很容易出现数值稳定性问题,需要使用较小的时间步长来解决。因此,很多研究者开始探索一种整体方案,Zarifi等[7]以及Akbay等[8]先后证明通过整体方案可以使用更大的计算时间步长并获得更好的系统稳定性。不同方案的选择受流体和固体所使用的表示方法影响。由于固体的静止状态形状很容易定义,因此通常使用拉格朗日网格表示法对其状态进行更新[9];相反,流体由于没有静止状态形状,因此通常使用欧拉网格表示法进行模拟[10]。这使得在流体和固体交界面以相同的法向速度移动需要额外的处理方案,Batty等[11]通过将力离散到欧拉网格表面来近似计算不规则表面,而Zarifi等[7]则通过更加复杂的cut-cell方法,以使边界结果更加准确。为了避免不同表示方法带来的耦合问题,很多研究者开始探索使用相同的方法来表示流体和固体[12-13]。另一方面,非线性固体模型对流固交互的真实性也有很大的影响。通常很多研究者会使用线性模型近似表示非线性固体模型,并通过迭代收敛得到非线性模型的解[14],但这也会占用大量的计算性能。而混合粒子-网格方法的提出[15-17]很好地缓解了这一问题。

可以看出,目前在基于物理的流固交互技术方面的研究主要从流体和固体所使用的表示方法出发,依据分区方案和整体方案的设计特点,结合真实性和效率问题优化流体运动方程的解算过程并选择合适的固体模型;其次,结合不同表示方法的特点选用特定的离散化方案,针对性地改进当前表示方法下实现效果;最后,从流固交互数值计算的加速策略中进一步提升系统的鲁棒性和效率。

1 流体运动方程

在基于物理的流固交互中,流体的运动方程通过一个偏微分方程表示,即Navier-Stokes方程(NS方程)[10]

其中,ρ为流体密度,u(x,t)是空间中流体速度,ut是的缩写,p表示压力,μ为运动粘度,f表示外力,如重力,是流体密度的物质导数。通常数学界倾Δ向于使Δ用ΔΔ表示拉普拉斯算子,而工程界使用2或·表示。NS方程从数学含义上表示牛顿流体的动量守恒(式(1))和质量守恒(式(2))。在特定情况下,也会增加关于气压、温度以及密度相关的状态方程[18]实现更丰富的流体效果。NS方程中主要考虑两点:1)应用到流体运动的牛顿第二定理;2)假设流体中的应力为扩散黏性项和压力项两部分。通常,对于非黏性流体,会将NS方程中的黏性项μΔu移除,并称之为欧拉方程。而对于不可压缩流体,则,即式(2)可以简化为。

2 固体模型

随着基于物理流固交互技术的不断发展以及固体本构模型的引入,在交互过程中使用的固体模型也越来越真实和丰富。根据固体的应力应变关系,大体上可以将其分为两大类:理想的不能形变的刚体以及可以进行弹性和塑性形变的软体或形变体。

2.1 刚体

刚体是流固交互中最常见的固体模型。通常自然界中的任何固体都会发生一定的形变,因此刚体是流体交互中的一种理想模型。在这个理想的限定下,刚体所有点的位置可以通过6个自由度来表示。首先,定义刚体的质心为空间中的一点,获得表示位置的3个自由度信息。其次,以刚体的质心为定位点,就可以得到刚体内任意一点基于质心的3个自由度信息。利用刚体中所有点彼此之间保持固定距离的约束关系,就可以得出刚体运动的规律。

Baraff等[19]介绍了完整的刚体模拟方法。通过将刚体的质心视为坐标原点,以此方便地将坐标系固定到刚体上进行运动分析。通常,刚体上的点相对于质点的坐标系称为物体空间,而将定义所有对象的公共坐标系称为世界空间。刚体的物体空间和世界空间如图1所示。

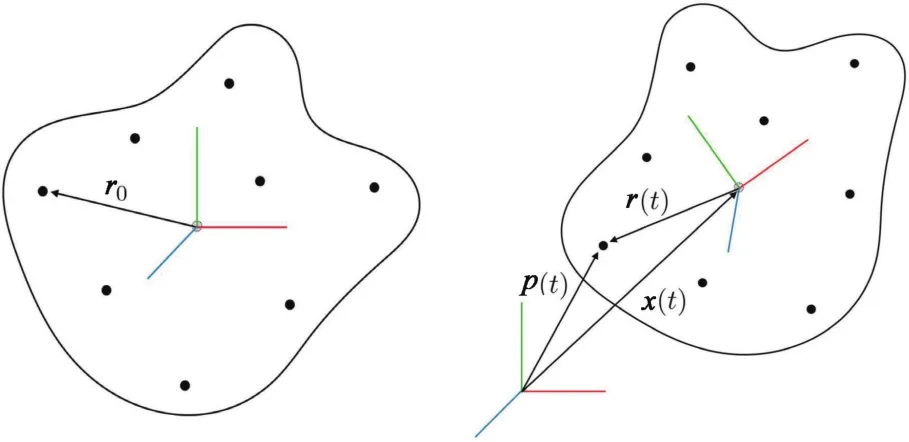
图1 物体空间(左)和世界空间(右)Fig.1 Object space(left)and world space(right)

在时刻t,当刚体中的某一点在物体空间r0处,刚体质心在世界空间x(t),而刚体的方向可以通过一个关于质心的旋转矩阵R(t)描述。那么,该点的世界空间坐标可以表示为

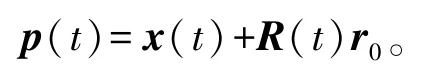
2.2 形变体

2.2.1 线性弹性模型

在基于物理的流固交互场景中,线性模型是常见的非线性弹性理论的简化,描述了物体如何形变以及如何将外部力转化为内部应力。线性弹性模型的基础线性化假设是:1)无限小的应变或小的形变,2)应变和应力之间是一种线性关系,3)仅适用于不会产生屈服的应力状态。

线性弹性模型的边界条件通过3个关于线动量平衡的张量偏微分方程和6个最小应变-位移关系控制。整个偏微分方程系统由一组线性算术本构关系组成。线性弹性模型的控制方程[20]为

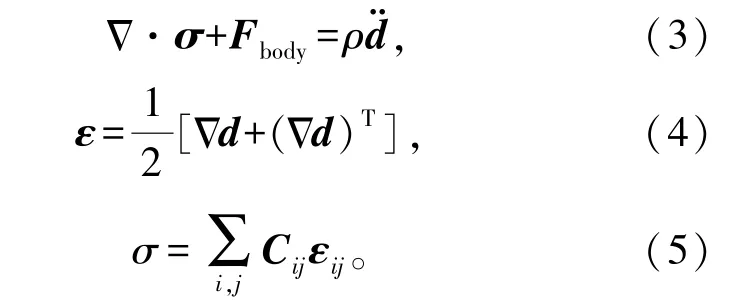
式(3)为由牛顿第二定律推导出的形变体运动方程,式(4)为应变-位移方程,式(5)为由胡克定理推导出的形变体本构方程,对于弹性材料,胡克定律表示材料的运动行为并关联应力和应变的关系。其中,σ是柯西应力张量,ε是无限小应变张量,d为位移向量,C表示刚度Δ张量,Fbody是单位体积所受的力,ρ为质量密度,表示Nabla算子,d¨表示位移关于时间的二阶导数。

2.2.2 超弹性模型

随着流固交互研究的不断发展,研究者们发现线性弹性模型并不能准确地表示弹性材料的真实行为。对于可以产生较大形变的材料,其应力-应变关系可以定义为非线性的、各向同性的、或不可压缩的且通常依赖于材料特有的应变率。而超弹性模型提供一种表示材料应力-应变关系的方法[21]。

最简单的超弹性模型是Saint Venant-Kirchhoff模型,它仅仅将线性模型几何扩展到非线性领域。该模型存在一般形式和各向同性形式,分别如下:

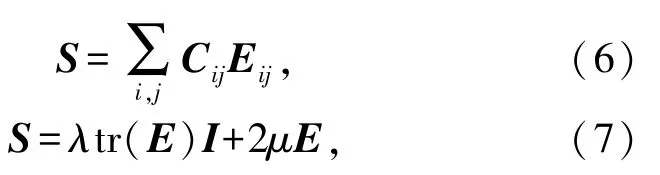
其中,S为 Piola-Kirchhoff第二应力张量,E为Lagrangian-Green应力张量,C表示刚度张量,λ和μ为 Lamé常数,I为单位矩阵。Saint Venant-Kirchhoff模型的应变-能量密度函数为

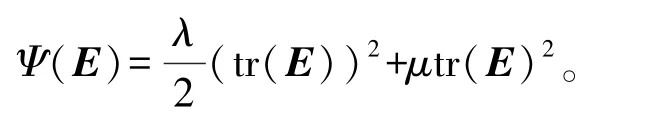
其他常见的非线性模型还有Neo-Hookean模型[22]和Fixed Corotated模型[23]。

3 表示方法和空间离散化

3.1 欧拉和拉格朗日表示法

在流固交互中,不同的表示方法对流固交互的实现效果有直接的影响。在经典场论中[24],拉格朗日表示法是指观察者跟随在空间中随时间移动的单独的流体包来观察流体运动的一种方式。绘制流体包随时间运动的位置可以获得该包的运动踪迹。拉格朗日规范可以视为坐在船上并随河水漂流。欧拉表示法是指聚焦在流体随时间流动的空间中某一指定位置上来观察流体运动的方法。欧拉规范可以看作在河岸边看河水流过某一固定的位置。

拉格朗日和欧拉表示法有时可以不严谨地表述为拉格朗日和欧拉参考系。然而,通常拉格朗日或欧拉表示法可以应用于任何观察者参考系中,并且可以用于基于任何坐标系统的参考系中。

在计算流体动力学或计算机图形学中,欧拉模拟使用固定的网格,而拉格朗日方式以随速度场移动的模拟节点为特征。

在欧拉规范中,流场用位置x和时间t的函数表示。例如,流场速度可以通过函数u(x,t)表示。同样,流场的压力和密度可以分别表示为p(x,t)和ρ(x,t)。通过这些函数的行为就可以确定整个流场。在拉格朗日规范中,将整个流体分割成一个个单独的流体包,这些流体包随时间移动,且由某个与时间无关的向量场x0标签化。通常,x0表示初始时刻t0流体包的质心位置,并以这种方式来分析物体随时间推进可能的变化。在拉格朗日规范描述中,流场通过在给定时刻t流体包x0的位置函数X(x0,t)表示。通过追踪这些随时间移动的流体包的特性和运动可以确定整个流场的特性。

以图2为例,在欧拉规范中,在烟囱上部位置O放置一个温度计,记录与时间t有关的函数T。当不同的烟雾粒子流经点O的时候,温度计的值T会发生变化。给定O点温度为T(x0,y0,z0,t),那么整个场中的温度可以表示为T(x,y,z,t),其中x,y,z与时间t无关。然而,在拉格朗日规范中,温度计则被依附在烟雾粒子A上,有TA=TA(t)。如果知道每个粒子随时间变化的位置函数,就可以将拉格朗日规范转化为欧拉规范。

图2 流场表示方法示意图Fig.2 Illustration of flow field specification

根据上面的陈述,这两种规范有如下关系:

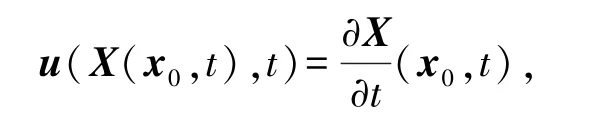
等式两边描述了在时刻t,标签为x0的流体包或粒子的速度。

3.2 空间离散化

NS方程是一种偏微分方程,除了一些较为简单的线性情况外,大多数情况下很难得到解析解。由于计算机的内存空间有限,所以对这些问题的离散化是必要的,进而可以通过数值方法获得偏微分方程的近似解。常见的空间离散化方法有:有限差分法、有限元法、有限体积法、谱元法、格子玻尔兹曼方法、边界元方法等。本文仅对常用的有限差分方法和有限元法进行简单的介绍。

由于有限差分方法和有限元方法相对容易实现,目前有限差分方法[25]和有限元方法[26]已经是求解偏微分方程数值解的最常见的方法。

4 时间离散化

在流固交互计算中除了进行空间离散化,还必须对时间进行离散化。为了形成动画,通常需要以固定的频率按时间序列计算下一时刻的输出结果。尽管可以选择不同尺度的时间步长,但是通常采用一个固定的时间步长来简化问题并避免伪影。虽然,目前在实际的模拟中每一帧仍需要计算多个时间步,但是大多数最新的动画系统中已经尽可能地减少每帧的时间步数。

4.1 显式时间积分

显式时间积分是指在更新时刻t+Δt的状态的时候,仅使用时刻t的量计算。常见的欧拉积分器

就是一种显式积分器,式(8)中,通过时刻t的位置x(t)和速度u(x,t)显式地计算时刻t+Δt的位置x(t+Δt)。还有很多类似的积分方法,但具有不同的特性。在研究此类积分器的时候,重要的是,对于特定应用而言重要的属性,可能对于计算机动画而言并不重要,并且看起来非常相似的积分技巧在实际中可能会有非常不同的表现。目前常见的显式积分器包括:梯形法积分、中点法积分以及辛欧拉积分器。

4.2 隐式时间积分

显式时间积分通过系统中当前时刻的状态计算后一时刻的系统状态,而隐式时间积分通过解算包含当前时刻系统状态和后一时刻系统状态的方程,以获得最终的解。隐式方法比显式方法实现难度更大,但是在解决某些刚性问题的时候,显式时间积分需要很小的时间步长来维持数值稳定性。为了解决这类问题并获得更高的精度,通过隐式方法就可以在较大时间步长的条件下以较少的计算量实现。

由于隐式方法不能直接处理所有类型的差分算子,因此在使用隐式方法的时候需要利用算子分割方法,这是隐式方法的主要局限性。

5 流固交互方法

根据交互场景中流体和固体所使用表示方法的差别,流固交互方法大致可以分为四类:欧拉流体和拉格朗日固体的交互、拉格朗日流体和拉格朗日固体的交互、欧拉流体和欧拉固体的交互以及混合的粒子网格方法,每种交互类型中根据具体实现方法的不同,又可以进一步划分。

5.1 欧拉流体和拉格朗日固体交互

5.1.1 MAC法

欧拉流体方法最早应用于计算流体力学领域,1965年,Harlow等[27]使用 MAC(Marker and Cell)方法和有限差分形式的NS方程,进行了不可压缩流体和刚体的交互模拟,并实现了滑动和非滑动边界条件。随后,Foster等[28]首次将MAC交错网格引入计算机图形学,通过解算二维或三维空间的NS方程,实现一种可控的复杂行为流固交互技术,其中固体通过拉格朗日网格法表示。但是,该方法中流体只能实现与网格对齐的不可移动的固体交互,处理曲线边界会出现体素化伪影。为了解决参数化曲线边界伪影问题和移动边界条件问题,他们[29]又使用半拉格朗日方法和水平集方法,分别计算法向和切向速度分量,通过速度场获取隐式表面。但是这个方法只能处理在一个网格节点中存在一个多边形面的情况,当网格分辨率较低的时候只能按照多个边的平均法线处理。Rasmussen等[30]提出使用粒子水平集的方法,结合移动网格窗体技术,实现了更加丰富的流体飞溅效果。但是流固交互边界的体素化伪影问题依旧存在。

5.1.2 ALE法

1974年,Hirt等[31]首次提出了ALE(Arbitrary Lagrangian-Eulerian)方法。Feldman等[32]使用基于速度的非结构化四面体网格表示欧拉流体,利用基于半拉格朗日的ALE方法,进行表面追溯。但是流体形变过程中的网格重建操作会消耗大量的计算机性能,同时数值耗散现象明显。Klingner等[33]利用非结构化的自适应网格改进上述数值耗散问题,但是网格重建问题依然存在。

5.1.3 Rigid Fluid法

Carlson等[34]通过拉格朗日乘子定义固体内部速度场并约束固体运动,从而将固体视为欧拉流体,实现流体和固体间的双向耦合交互。但是这种方法在进行流体和很薄的固体交互时,由于流体会透过固体约束,发生漏液现象。Guendelman等[6]改进了上述方法,通过使用低维度的三角形表面,处理无限薄的固体模型,消除漏液现象。

5.1.4 cut-cell法

Roble等[35]使用cut-cell方法,将欧拉网格裁切成和不规则物体边界一致的形状,对规则的有限差分方法进行修改,结合相应的流体散度计算方法,使体素化网格可以更好地匹配物体细节。Batty等[11]将压力投影方法改写为动能最小化问题,通过计算使离散动能最小的离散压力值,保证生成对称正半定的线性系统,使解算速度提升两个数量级。但是都不能处理形变体问题。Robinson-Mosher等[36]使用固体速度作为边界条件作用于流体,并用流体的压力作用的固体,实现形变体的流体耦合处理,之后他们[37]通过分析形变结构的阻尼矩阵,获得对称正定线性系统,改进了之前的数值不稳定问题,但都不能实现流固间自由滑动。Zarifi等[7](图3)结合Chentanez等[38]提出的强耦合流固交互整体系统方案,使用cut-cell离散方案,实现自由滑动边界条件,对流体使用有限体积离散化,同时对固体使用有限元方法,有效避免了基于网格方法出现的阶梯状体素化伪影问题。

图3 使用cut-cell方法的流固交互Fig.3 Fluid-solid interaction by cut-cell method

5.1.5 流函数法

Ando等[39]使用流函数(Stream Function)代替压力投影方法,实现了一种无条件无散度的窄带流固交互方法。利用Helmholtz-Hodge分解可以直接计算出最终的速度,但是这种方法并不能很好地处理可压缩流体。

5.1.6 小结

欧拉表示法可以容易地实现流体的不可压缩性,MAC方法通过将速度和压力投影到网格上,使得空间离散化过程很方便,而其体素化伪影问题也可以通过cut-cell法得到缓解,但是欧拉流体数值耗散问题严重。同时,使用欧拉流体和拉格朗日固体交互很难实现整体系统方案,这使得时间步长和系统稳定性都受到一定的限制。

5.2 拉格朗日流体和拉格朗日固体交互

5.2.1 DSC法

Misztal等[40]基于拉格朗日形变单纯复形(Deformable Simplicial Complex,DSC)方法,使用非结构化四面体网格和有限元方法,将NS方程的解特征化为二阶优化问题。通过伪可压缩方程求解稳定的压力值,降低数值耗散现象,但网格重建和倒置问题突出。Clausen等[12]设计了一个局部的三维网格修复算法缓解大形变情况下网格倒置问题,可以鲁棒地分割或合并四面体网格。同时在四面体元网格上存储信息,并使用线性基函数进行插值。但是这种局部方法对时间步长要求严格,网格重建问题仍需占据大量的计算时间。

5.2.2 SPH法

由于基于拉格朗日网格的方法需要频繁地处理网格的拓扑变化,因此Solenthaler等[41]引入了局部参考形的定义,利用光滑粒子流体动力学(Smoothed Particle Hydrodynamics,SPH)和表面重建技术,实现了融化和凝固效果。Akinci等[42]实现了SPH流体和任意形状的刚体的交互。通过边界粒子采样固体表面,解决不规则边界采样问题。而且粒子方法可以自然地模拟小尺度细节。但是上述两个方法在处理可压缩流体边界的时候会出现穿透问题。Peer等[43]直接从形变梯度上获取旋转信息,使用一阶连续的内核梯度修正算法进行旋转估计,结合不可压缩SPH方法,简化了边界条件计算过程。但是由于加入了更大的显式摩擦力项,导致时间步长被限制。Gissler等[44](图4)对固体表面进行粒子采样,将流体迭代解算器和固体SPH解算器相连接,通过使用大的时间步长显著地减少计算时间,并能和不同的SPH解算器相结合。

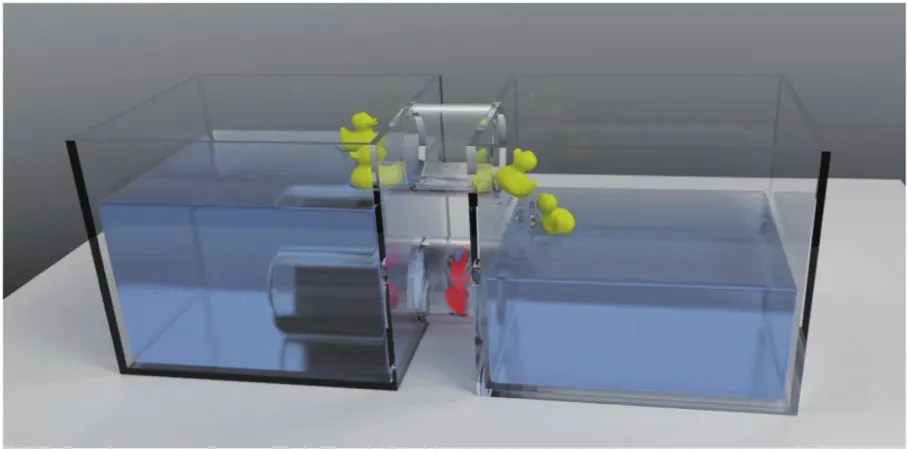
图4 使用SPH方法的流固交互Fig.4 Fluid-solid interaction by SPH

SPH方法在处理邻近搜索的时候需要消耗大量的计算性能,而且不能很好地构造隐式系统,并行计算很难实现。

5.2.3 PBD法

Macklin等[45]使用基于位置的动力学(Position Based Dynamics,PBD),提出一个易于并行的约束解算器,可以实时地呈现动画效果,兼顾简单性和鲁棒性。同时该方法改进了摩擦模型,增加了动摩擦和静摩擦效果。但是PBD没有使用基于物理的本构模型,真实性不足。

5.2.4 小结

拉格朗日方法常用的空间离散化拓扑结构主要为拉格朗日网格和拉格朗日粒子。拉格朗日网格(如DSC)方法,很好地解决了欧拉网格体素化伪影问题,但是其在处理大形变的时候网格重建和网格倒置问题十分明显,需要使用小的时间步长和特定的优化方法处理,对计算机性能要求较高;拉格朗日粒子(如SPH、PBD)方法,解决了网格拓扑变化问题,并能实现次网格细节,但是单纯的粒子法需要昂贵的邻近粒子搜索操作,这进一步提高了对计算机性能的要求。不过,拉格朗日流体和固体间的交互便于构建整体方案,使整个系统的真实性更明显。

5.3 欧拉流体和欧拉固体交互

5.3.1 IBM法

Peskin等[46]在生物流体力学领域,使用浸入边界法(Immersed Boundary Method,IBM)实现了流体和固体的交互。在欧拉视角的笛卡尔网格上对浸入边界方程进行空间离散化,并通过二阶龙格库塔方法实现时间离散化。随后,Levin等[47]将这个方法扩展到弹性固体,并且可以直接模拟体积化的数据模型。解决了对非线性形变的碰撞检测和处理问题,并消除了黏性伪影问题。由于使用欧拉网格离散化,易于GPU并行计算。但是,该方式对时间步长要求较高,同时不适用于无限薄物体的模拟。Teng等[13]结合上述欧拉固体表示法和相应解算器,实现了完全基于欧拉方法的不可压缩流体和形变体的双向耦合。通过使用隐式积分器,降低对时间步长的要求。但是,这种方法只能处理单向流现象。

5.3.2 EOL法

Sueda等[48]结合拉格朗日方法和欧拉方法的特点,提出了一种包含简化节点和欧拉节点的Eulerian-on-Lagrangian(EOL)方法。该方法可以鲁棒、高效、准确地模拟包含大量约束的系统。随后,Fan等[49]利用EOL方法不需要显式离散化的特点,将高频形变的情况用欧拉方法处理,并提出一个基于最小二乘法的接触感知解算器。在保证系统稳定的同时使时间步长最大。但是由于显式地处理弹性力,导致系统可能出现不稳定现象。接着,他们[50]对人体肌肉使用EOL方法处理体积守恒和大形变问题,实现了肌肉骨骼等关节组织的近距离接触模拟。该方法可以直接通过MRI数据建立肌肉模型,但只能实现较简单的肌肉运动效果。Sachdeva等[51]利用EOL离散方法,消除了准静态方程中不必要的纵向自由度,同时维持横向运动,实现了对薄/细东西的模拟。该方法简化了肌腱和骨头间的碰撞处理问题,在较大时间步长的前提下实现了高度刚性的肌腱模拟。但是该方法对参数过于敏感,且实现的效果较为简单。Weidner等[52]将EOL扩展到处理三维空间中的二维物体,模拟布料和尖锐集合体的交互,通过在布料中插入EOL顶点,实现尖锐交互点布料的精准弯曲效果,同时避免了过约束导致的锁定问题和抖动问题,但是这种方法网格重建效率并不高。

Li等[53]使用欧拉固体的模拟方法,提出了一个现存动画管线的后处理技术。通过建模二维空间的任意拓扑结构的超弹性膜,可以方便地实现覆盖到任意物体上的皮肤或薄膜效果。利用类似于纹理贴图的方法,可以使用低分辨率网格实现高分辨率的表面细节。

5.3.3 小结

欧拉固体继承了欧拉表示法的优势,IBM方法可以直接模拟体积化的数据,并且便于GPU并行计算;EOL方法虽然是在拉格朗日空间使用欧拉节点,但是其本质仍是欧拉方法特性。欧拉方法可以隐式地进行空间离散化,不过,在处理弹性固体的时候,欧拉方法对时间步长要求较高。

5.4 混合粒子-网格法

5.4.1 SPH粒子-网格法

Hong等[54]使用SPH结合欧拉网格,基于SPH涡度约束方法实现了多相流气泡和水的交互,并利用新的气泡模型呈现出次网格气泡细节。但对时间步长要求较高。Patkar等[55]改进上述方法,基于Rayleigh-Plesset方程,实现了气泡振荡和合并现象的模拟。利用新的基于涡度的气泡播种机制,模拟交互过程产生的气泡,并实现了气泡的可压缩性和不同尺度气泡的无缝过渡。Losasso等[56]通过区分聚集和扩散水域,并分别使用水平集方法和SPH粒子模拟。但是,这种方法在计算粒子密度时存在一定误差,而且可能产生数值噪声伪影。Lee等[57]使用 SPH逃逸粒子并结合BFECC(Back and Forth Error Compensation and Correction)和CIP(Constrained Interpolation Profile)方法确保了二阶精度的位置更新。Gao等[58]使用欧拉网格和SPH粒子实现了高速和低速气体流。但是这种方法在物理上并不严格的能量守恒。Raveendran等[59]通过对局部SPH粒子进行密度修正,并利用粗网格上的泊松解算器计算无散度的速度场。这种方法消除了纯网格方法的体素化伪影,并加快了系统收敛速度。Zhu等[60]使用SPH-FLIP方法进行流体模拟,可以生成并保留湍流细节,但是这种方法的效率并不是太高。

5.4.2 Voronoi/Power diagrams法

Sin等[61]基于拉格朗日粒子方法,通过在采样点上计算Voronoi来处理压力投影。使用散度定理确保Voronoi单元无散度,并处理了复杂的边界条件。这种方法灵活地结合基于点和基于网格的方法,保证了质量守恒。Brochu等[62]提出了一个简化的Voronoi/Delaunay网格速度插值方案。使用压力采样方法,结合基于网格的曲率估计和流体边界条件,准确地获得表面张力。这种方法虽然消除了显示表面追溯方法产生的噪声,但是其他伪影问题依然存在。De Goes等[63]使用拉格朗日幂粒子法,将流体粒子视为体积包,并通过Power diagrams时间序列来描述流体运动。通过基于网格的压力投影,准确地计算空间中流体体积,有效减少数值阻尼和粒子漂移问题。

5.4.3 FLIP/PIC法

1995年,Sulsky等[64]将FLIP/PIC扩展到固体力学,使用基于物质点和计算网格两种表示法,消除拉格朗日网格的大形变纠缠问题,并利用网格计算空间梯度变化,充分展现了物质点法的优势。Zhu等[65]通过改进水模拟器参数,实现对沙子的模拟。利用粒子准确地进行表面追踪,并使用网格执行不可压缩性和边界条件。Hong等[66]使用FLIP方法,基于深度和雷诺数,实现了不可压缩流体的模拟,并量化了流体不同区域的形变能力。McAdams等[67]基于FLIP流体解算器,实现了头发的批量交互和体积守恒计算。虽然,基于拉格朗日方法的自碰撞检测可以准确地处理头发间的精细交互,但是需要较高的网格分辨率,且存在角动量耗散问题。Han等[68]基于物质点法实现头发、线股等共维模型的摩擦接触和自碰撞处理,利用拉格朗日自由度减少伪影问题,但出现线股压缩现象时会导致能量不守恒,且不能很好地模拟刚体运动。Stomakhin等[69]基于连续介质力学,提出弹塑性本构模型,可以自动地处理雪的自碰撞和断裂效果,并使用半隐式方案可以处理大范围的刚度问题。但是,雪的参数需要手动调整,且碰撞处理为非滑动边界条件。随后,他们[70]提出了流体本构模型的分割方法,使用物质点法模拟热传递、熔化和凝固现象,并提出增强型MPM方法,实现流体不可压缩性,但仍不能实现自由滑动边界条件。Yan等[71]基于Noyes-Whitney方程,实现了流体间混溶和不混溶的多流体方案,但仅实现了弱可压缩流体。Hu等[17]使用移动最小二乘法和CPIC方法,利用颜色距离场实现不连续速度场切割,但无法处理次网格细节。Fang等[72]使用接触面离散积分点方法,改进了传统物质点法非滑动边界条件,实现非线性弹性固体和不可压缩流体间的自由滑动。但在处理固体和固体交互时会出现数值不稳定现象。Daviet等[73]利用材料流变学,并结合体积摩擦和Drucker-Prager屈服准则,模拟真实自由流动的颗粒状物质。但只能实现均质材料的模拟。Tampubolon等[74]使用连续混合理论模拟滑坡或泥石流等湿沙现象,利用动量交互项完成多个类型物质间的动量转移并保证动量守恒,但不能实现毛细现象。Gao等[15]改进了上述方法,使用Drucker-Prager弹塑性流体准则,实现多网格流体预处理解算器。利用新的粒子密度估计方法,实现多孔材料和水的交互。但由于使用显式积分方案,在相对速度过大时会出现数值伪影。Fei等[75](图5)依靠混合理论更新速度场和饱和度变量,并充分考虑布料中多孔材料的微观结构,实现了布料对水的吸收和滴落效果。但是这种方法需要较高的网格分辨率和较小的时间步长。

图5 物质点法实现水透过毛巾Fig.5 Water through towel by material point method

5.4.4 小结

混合粒子网格方法因其结合了欧拉网格和拉格朗日粒子的优势,在近些年吸引了越来越多研究者的关注。SPH方法通过背景网格可以提高邻近搜索速度,但也引入了额外的计算复杂度;维诺图的引入虽然使速度计算更加方便,但是通过估计的方法导致整个系统的物理性和真实性缺失;物质点法通过插值函数将粒子和网格联系起来,使用网格计算压力,并利用粒子进行携带物质信息,可以实现多种物质的模型,但是插值函数的引入也引起了额外的数值耗散问题。

5.5 对比说明

表1总结了各类典型的流固交互方法的具体实现和规模效率信息。其中,详细介绍了文献中的具体实现方法和表示方法信息,并对空间离散方案和时间积分器进行对比。由于各个文献中使用的硬件信息差别很大,因此通过规模和效率两个维度并不能完全论证不同文献中算法的优劣。不过,从表中仍可以看出,基于物理的流固交互方法很难达到实时性,尤其在使用粒子法的文献中,为了追求更加真实的交互效果,通常都需要几分钟才能计算一帧图像,这也是未来需要优化处理的研究方向。

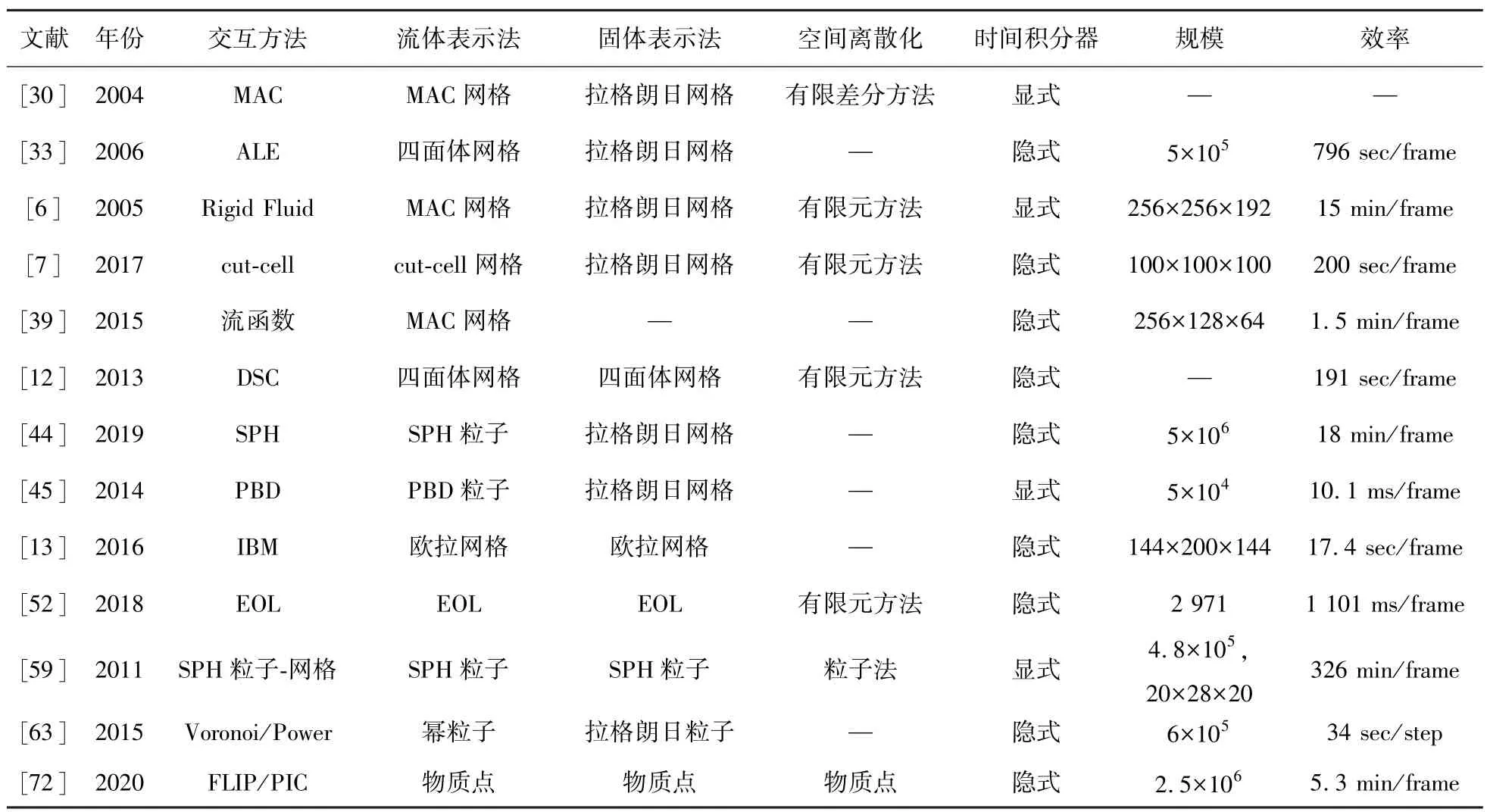
表1 各种流固交互技术对比Tab.1 Comparison of fluid-solid interaction methods

6 碰撞检测方法

碰撞检测是流固交互中必要的处理步骤,根据处理的先后顺序,通常分为两步:碰撞检测和碰撞响应。碰撞检测过程一般基于距离进行碰撞判断,当两个物体出现交点或物质点发生穿透,则判定碰撞发生;而碰撞响应通常基于反射定律或特定的边界条件进行处理。Kelager等[76]详细介绍了SPH方法中的碰撞检测边界条件,由于SPH粒子在边界处邻近粒子密度降低,导致边界处粒子出现过高的黏性。Fujisawa等[77]通过修改SPH邻近粒子密度计算方法,改善边界黏性聚集问题。Sifakis等[78]将碰撞响应设置为非线性约束,解决复杂的、多层布料的碰撞问题。该方案可以产生一个对称正定的线性系统,比传统贪婪算法速度提高两个数量级,但是该方法并没有优化碰撞检测方法,仅提高了计算速度。McAdams等[79]提出一种可以在不规则体素化域上处理任意混合的狄利克雷边界条件和诺依曼边界条件的纯几何方案。Müller等[80]通过在物体间插入空气的方法,利用单边约束条件自动、鲁棒地处理纠缠问题和布料模拟中的穿透问题。

7 加速策略

7.1 自适应方法

在流固交互领域,自适应方法因其局部优化的特性,一直都是研究者们的重点研究领域。自适应方法将主要的计算工作集中在视觉重点区域,通过对计算资源的合理分配,达到加速的目的。通常自适应方法的类型和不同的表示方法相关联,包括自适应网格方法、自适应粒子方法、自适应插值函数方法、自适应核函数方法等等。Losasso等[81]提出一种不受限的八叉树数据结构和相应的离散方法,并获得对称正定的线性系统。Ando等[82]使用空间自适应的FLIP方法,减少压力解算的复杂度,增加系统鲁棒性。但这种方法会产生动量伪影。Ferstl等[83]使用自适应八叉树网格和六面体有限元离散化方法,利用几何多网格解算器,获得高效的收敛率。Setaluri等[84]基于硬件加速机制和虚拟存储管理系统,提出金字塔状的稀疏均匀网格数据结构,通过避免间接的内存访问并利用自适应多网格预处理共轭梯度解算器,加速压力解算过程。Aanjaneya等[85]通过使用幂图和金字塔式的稀疏均匀网格,增强泊松算子的规范性。Gao等[86]提出一种自适应广义插值方法,引入GIMP范式和离散化框架,实现高效的内存读取和并行计算。Chentanez等[87]将空间分为tall cells和cubic cells,简化数据结构和算法,便于系统并行计算。Goswami等[88]基于并行分块技术,将WCSPH流体分割成不同的计算域,获得了两倍的速度提升。

7.2 高速解算器

在解算流固交互过程中,很多系统求解精确解的过程十分困难,甚至不存在实际的解。为了计算方程的近似根,通常使用牛顿迭代法求解。Mazhar等[89]提出一种加速的投影梯度下降方法,对比传统的高斯赛德尔和雅可比方法,收敛速度更快,且易于并行。Aanjaneya等[90]基于域分解理论和舒尔补码方法,使用克利罗夫计算器代替传统的泊松解算器,利用multigrid v-cycle预处理器加速共轭梯度求解。

7.3 硬件并行加速

研究者为了追求更加逼真的流固交互效果,在交互系统中使用的粒子和网格数量也越来越多,因此许多研究者都考虑使用并行技术加速整个系统的计算效率。早期的解决方法通常是使用基于 CPU的 SIMD指令[91]或 OpenMP[92]进行加速。但受限于CPU的设计架构,其在处理大规模并行加速场景中优势并不明显;相反近年来,由于GPU的带宽优势,越来越多的研究者基于GPU架构设计并行加速策略。Wu等[93]使用FLIP方法结合GPU并行加速策略,实现了千万级粒子的流体模拟场景。Hu等[94]提出基于GPU加速的Taichi图形学编程语言,可以直接选择不同的并行加速架构。

8 研究趋势预测

近年来,随着计算机硬件的不断发展,研究人员也可以从更多的角度分析并优化流固交互中的数值方法。结合近些年的研究现状,未来可能从以下几个方面推进。

1)大规模场景的实时交互。

目前,在小规模场景中,基于物理的流固交互展现出十分真实的模拟效果,然而在较大规模场景中,单纯的基于物理的流固交互方法并不能很好地得到应用。由于神经网格等机器学习算法的流行,将基于物理的流固交互技术和机器学习相结合将是未来的热点话题。此外,基于高度场和缓坡方程研究大规模流固交互场景的实时模拟技术也具有重要的意义。

2)基于成熟模型,开发市场化应用。

现有的流固交互技术,已经可以实现非常逼真的交互场景。目前,加拿大的sideFX公司、美国的NVIDIA,以及中国的泽森科工都开始在图形学可视化编程软件领域进行探索以降低影视特效、游戏制作、医疗仿真等非专业图形学人员的使用门槛。未来的研究重点将进一步提高软件的扩展性、交互性以及便利性。

3)结合计算机硬件,改进数据结构。

通过结合计算机硬件读写特点,改进流固交互数据存储形式,在计算机带宽不变的情况下,速度将得到有效的提高。传统的计算机软件,在存储优化这方面主要依靠编程人员的个人技巧,在实现相同的场景中,不同人开发的代码效率也各不相同。特别是在流固交互场景中,百万级甚至千万级的粒子数量,使得单次读写微秒级的差别也会放大百万倍。因此如何使数据存储结构更方便地读写和并行计算,将是未来流固交互领域的一个重要研究课题。

9 总结

本文系统地介绍了近年来流固交互技术相关研究工作。为了让人们在计算机虚拟世界中感受到真实的交互场景,流固交互技术已经发展了几十年,但仍有很多方面需要进一步探索。

基于物理的流固交互技术因选择的表示方法不同,处理方案也各不相同,但各种方法都存在优势和劣势。基于欧拉网格的方法在离散化、压力解算和并行计算方面更有优势,基于粒子的方法在表现流体细节、大形变处理方面更方便,因此基于粒子-网格的混合方法得到了大量研究者的重视。然而,基于物理的流固交互技术在大规模场景搭建、实时交互、市场化应用等方面仍面临着很多问题。

本文从计算机图形学领域中流固交互文献所使用的表示方法角度,总结了目前相关研究中通常使用的具体实现方法和技术,有助于理解基于物理的流固交互中的数值方法和关键技术。