基于LSTM的塔架振动状态监测研究

苏连成,朱娇娇,郭高鑫,李英伟,姜浪朗

(1.燕山大学 电气工程学院,河北 秦皇岛 066004;2.中国重型机械研究院股份公司,陕西 西安 710018;3.燕山大学 信息科学与工程学院,河北 秦皇岛 066004)

0 引言

近年来,风能作为一种清洁的可再生能源迅速发展,风电机组装机规模不断扩大。塔架作为风力发电机组的主要支撑装置,它将机舱和风轮托举到所需的高度,使机组更充分地吸收风能。随着风电机组单机容量的提升,塔架的高度也不断增加。在风电机组的整个寿命周期内,塔架受到风轮、机舱、自身重量以及各种风况引起的复杂动载荷作用[1]。如果塔架发生过度倾斜、振动异常等问题,易出现机组输出功率减少,还可能引起极端载荷,甚至发生倒塔等安全事故[2]。因此发展有效的塔架振动状态监测技术,及早发现风电机组早期故障隐患,对提高风电场运行的安全性和经济性具有重要意义。

国内外许多学者对塔架振动信号和结构响应等方面进行了研究。郭鹏等[3]采用非线性状态估计的方法建立塔架振动预测模型,以预测值与真实值的残差作为评判标准,对塔架振动状态进行监测。房宁等[4]采用主元分析的方法建立塔架与其相关变量之间的关系模型,通过计算霍特林统计量和平方预测误差实现对塔架振动状态的监测。文献[5]建立高斯回归过程塔架振动预测模型实现对叶轮桨距角不对称的故障诊断。成立峰等[6]通过实验说明风速和湍流是风机振动最主要的激励源。文献[7]使用概率密度演化的方法获得随机载荷下风机结构的可靠性。文献[8]将风机的运行工况按风速、转速和桨距角分为7种情况,分析指出风电机组塔架振动状态受风电机组运行工况影响。文献[9]研究了海上高大单桩钢风力发电机塔架在风、浪、流作用下在架设阶段的动力响应。文献[10]提出了一种改进的基于逐步辨识的海上风电机组塔架结构损伤预测方法。

上述不具有时间记忆能力的算法不能充分挖掘风电机组监督控制和数据采集(Supervisory control and data acquisition,SCADA)系统数据的复杂时序信息,导致风电机组塔架振动状态预测精度不高。长短期记忆(Long short-term memory,LSTM)网络可以结合当前和过去的信息很好地学习SCADA数据中的依赖关系,因此本文提出了一种基于LSTM网络的塔架振动状态监测方法,提高了预测精度。

1 基于LSTM的塔架振动状态监测

1.1 LSTM网络基本原理

递归神经网络(Recurrent neural network,RNN)与LSTM网络都是具备长期记忆能力的时间序列模型,RNN在计算的过程中会记忆网络之前的状态,这使得计算量和模型的计算时间大幅度增加。为克服这一缺点,LSTM在RNN的基础上,增加了遗忘门、输入门和输出门3个门结构有选择地记忆网络之前的状态,提升了模型计算速度。其中,遗忘门是选择地记忆部分时刻的输出,输入门是结合当前时刻的输入和上一时刻的输出改变当前状态,输出门是当前神经网络的状态改变后通过激活函数得到当前神经网络的输出。LSTM基本单元结构如图1所示[11]。

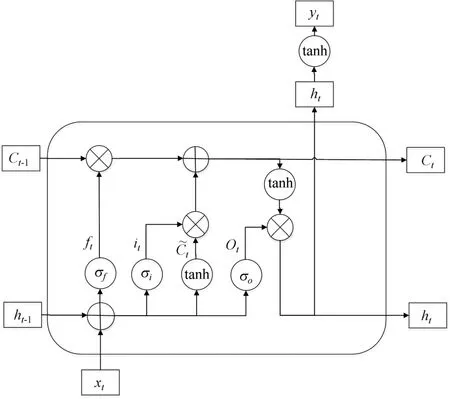
图1 LSTM基本结构单元Fig.1 The basic structural unit of LSTM

图1中,it为输入门,ft为遗忘门,Ct为细胞状态,Ot为输出门,ht为下一时刻的隐层函数,yt为下一时刻的输出。计算公式为

式中:Wxi,Whi,Wxf,Whf,WxC,WhC,WxO,WhO,Wy,分别为输入层到输入门,隐含层到输入门,输入层到遗忘门,隐含层到遗忘门,输入层到细胞状态,隐含层到细胞状态,输入层到输出层,隐含层到输出层,输出层对应的权重矩阵[12];bi,bf,bc,bo,by分别为输入门,遗忘门,细胞状态,输出门,输出层对应的偏置项。

1.2 模型评价

由于直接比较不能定量地描述模型的预测效果优劣,为更加准确地评价模型的预测精度,本文使用可以体现模型预测值与真实值残差大小的误差平方和(Sum of the squared errors,SSE)、均方误差(Mean-square error,MSE)和平均绝对误差(Mean absolute error,MAE)作为模型的评价指标,公式如下。

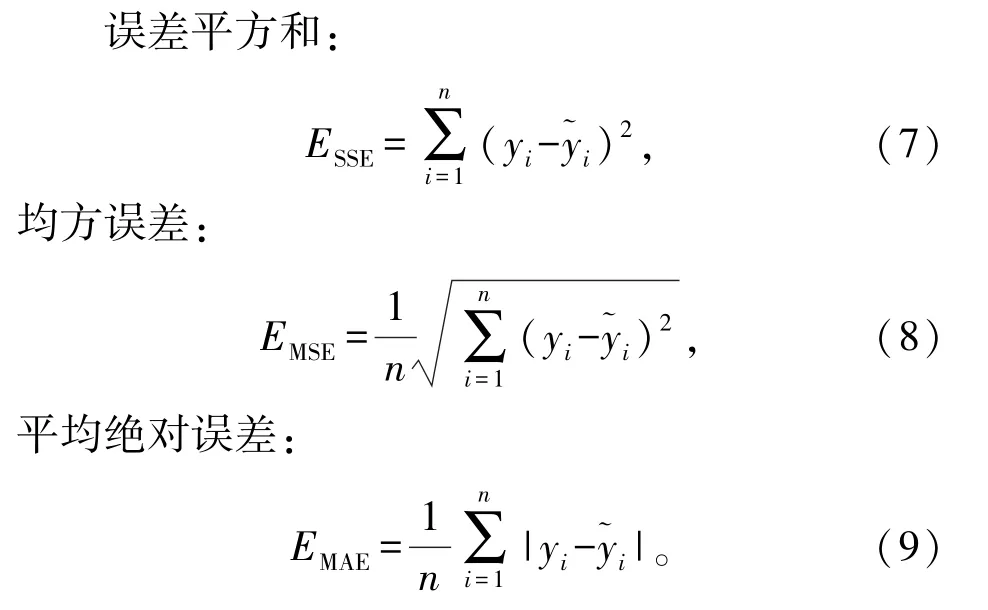
式中,yi和分别表示样本真实值和样本预测值[13]。误差平方和的大小表明模型拟合的好坏,均方误差是反映预测值与真实值之间差异程度的一种度量,平均绝对误差表示所有单个预测值与算术平均值的偏差的绝对值的平均,可以避免误差相互抵消的问题,准确地反映实际预测误差的大小。这3种误差函数作为模型的评价指标,可以定量地评估模型预测效果。

1.3 阈值确定与预警

使用正常数据训练LSTM模型后,设塔架振动预测值与真实值的残差为E,计算公式为

风电机组正常运行时,将选取的状态参量输入模型,得到预测值与实际值的残差较小[14]。当风电机组处于异常运行状态,如发生桨距角不对称、变流器等故障时,由于风机内部控制动作的激励导致塔架处于异常振动状态,此时输入变量与目标参量之间的关系将发生变化,使残差增大。根据模型训练得到的预测值与真实值的残差为随机变量,满足正态分布的原则,设置合适的置信度得出塔架正常振动时残差的上下阈值限。

2 SCADA数据处理

2.1 数据预处理

SCADA系统作为风电机组的监测基础,采集了大量与风机运行特性相关的变量[15-16],如风速、功率、机舱温度、环境温度、叶轮转速,齿轮箱转速、发电机转速、桨距角、电流、电压等上百个参数。其中包括风电机组正常运行的数据和异常运行的数据,还有一些空数据,通常不能直接使用。在对SCADA数据进行建模之前,需要对数据进行预处理,剔除风机运行的产生的空值和异常值。本文以某风电场双馈异步风电机组为研究对象,对该风电场26号机组1月～7月SCADA数据进行预处理。如图2所示,其中图2(a)为原始SCADA数据的风速-功率图,(1)区域为机组限功率数据;(2)区域为机组故障或传感器异常测得的数据;(3)区域为机组停机数据。图2(b)为预处理(即删除限功率数据、停机数据、空数据和故障数据)后的风速-功率图。

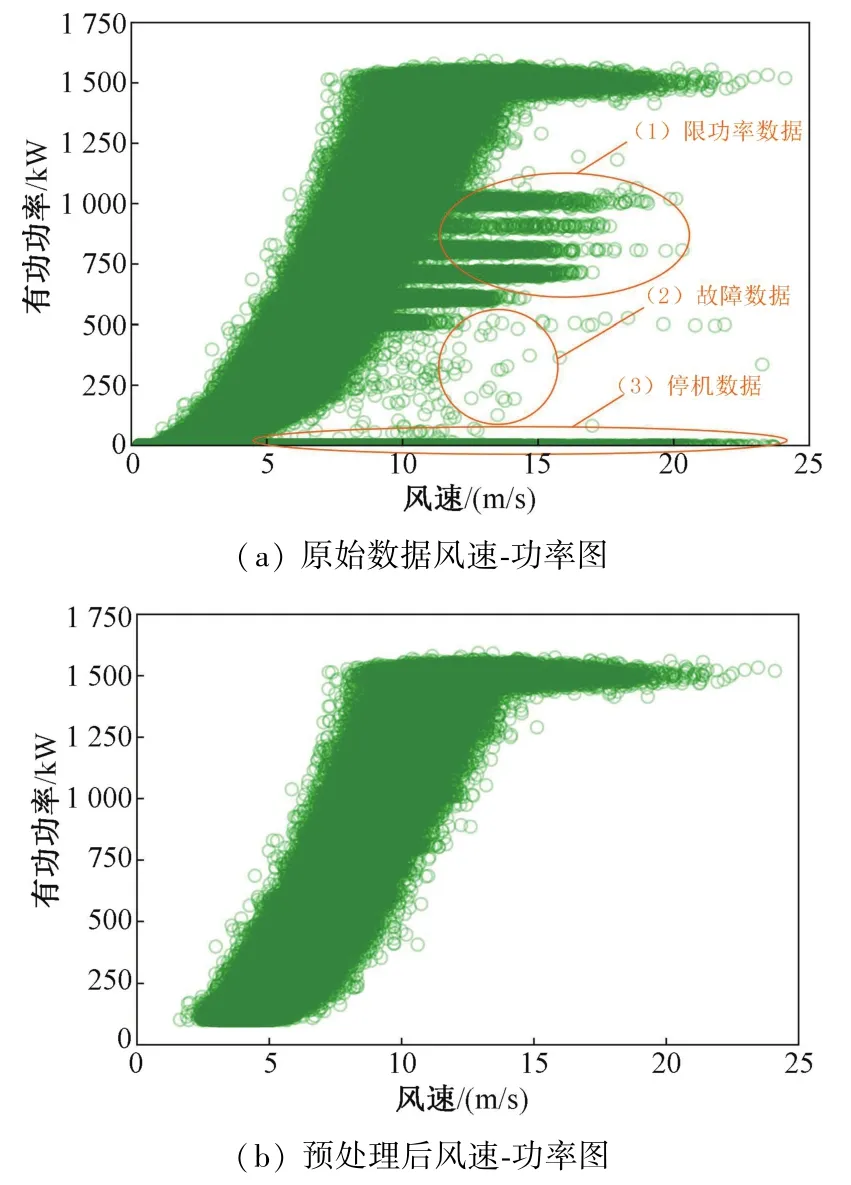
图2 26号风电机组风速-功率图Fig.2 Wind speed-power diagram of No.26 wind turbine

2.2 输入参数选择

SCADA采集数据变量种类繁多,若采用全部SCADA变量建立模型,不仅降低了数据的计算速度,也降低了模型预测的准确性。为提高模型的运算速度和预测精度,需要选取对目标变量影响较大的参数,本文引入了灰色关联度系数和最小角回归(Least angle regression,LAR)算法。

2.2.1 灰色关联度系数

灰色关联度是描述数据变化趋势的一种方法,数据曲线越平行,其灰色关联度系数越大。公式如下[17]:

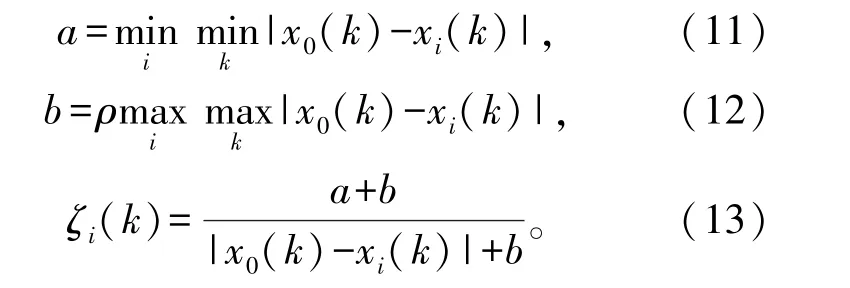
式中,x0(k)为母序列,xi(k)为子序列,ζi(k)为每个子序列与母序列之间的关联程度系数,大小从0到1,子序列与母序列的关联程度逐渐升高。

根据数据曲线间的一致性计算出的灰色关联度系数总为正值,而SCADA参数与塔架振动量之间不一定是正相关,因此结合LARS算法进一步明确塔架振动量的影响因素。

2.2.2 LARS算法

LARS算法是一种适合高维数据的回归算法[18],基于线性平方误差最小的原则,选择出与目标变量相关性较强的参量。给定数据{X,y},X∈Rn×m,y∈Rn其中xi∈Rn(i=1,2,…,m),找出最少的变量x1,…,xr,(r≤m)∈Rn,使其线性组合最大程度地接近y,约束条件为

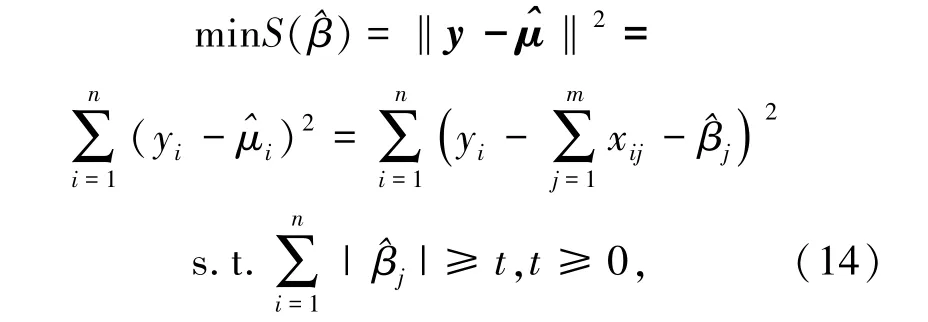
其中,(xi1,xi2,…,xim),yi分别为第i个样本的m个自变量和因变量,为第j个自变量的回归系数。LARS算法就是调节使上述公式的平方误差和最小。当t取较小值时,与因变量相关性较低的自变量回归系数将为0。

为监测塔架振动的状态,将塔架振动加速度作为目标变量。由于该机组的SCADA系统每30 s记录一次传感器测量的塔架振动数据,振动量的变化频率较高,采样频率较低,使用原始记录的瞬时值数据难以描述振动变化的真实情况,所以本文求取塔架振动数据10个值的滑动平均值,将节点100X方向滑动均值作为模型的目标参量。各参数与目标参量的灰色关联度系数与回归系数如表1所示,LARS回归系数β与算法迭代步数之间的关系如图3所示。

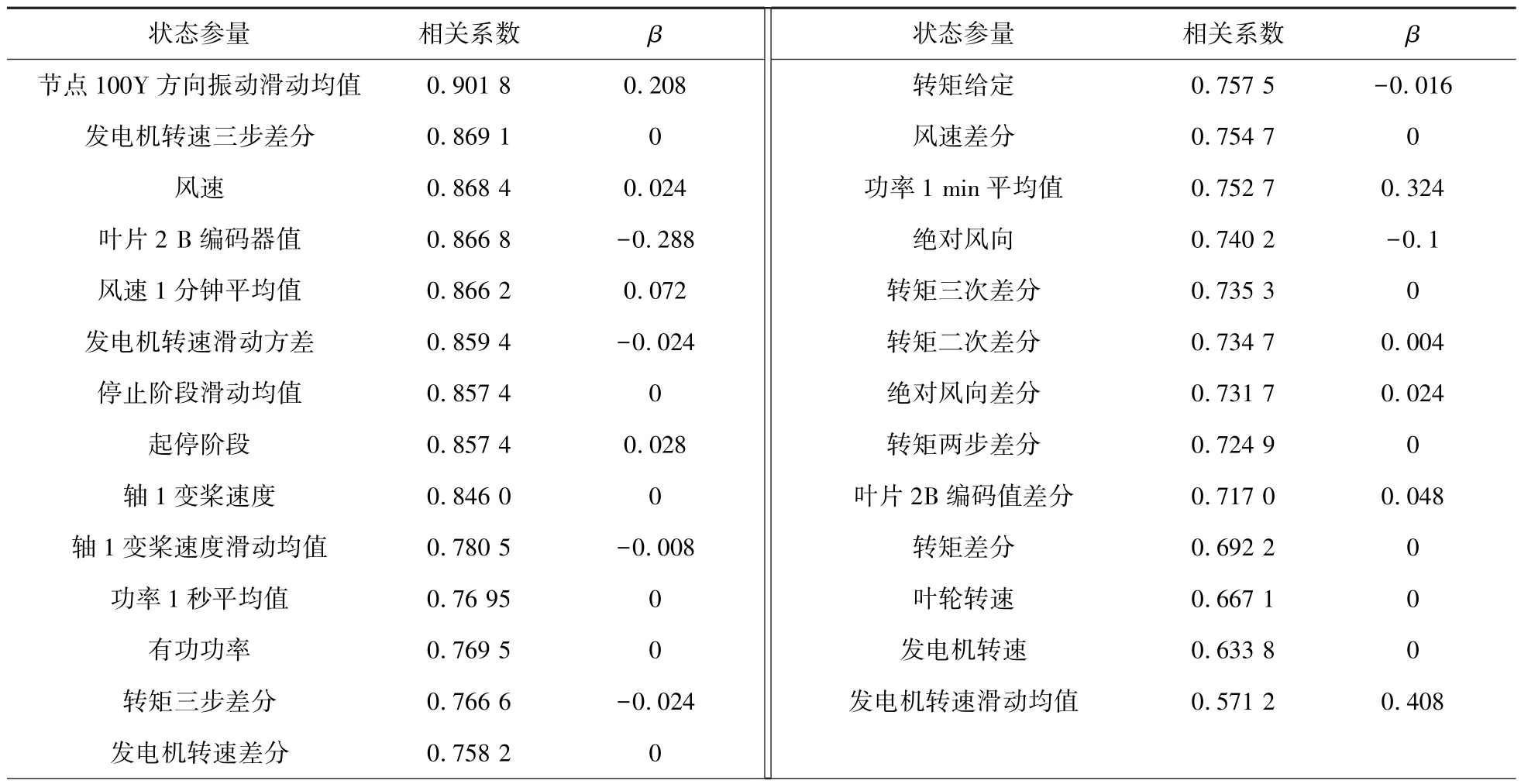
表1 各参数与输出参数灰色关联度系数与回归系数表Tab.1 Table of gray correlation coefficient and regression coefficient between each parameter and output parameter

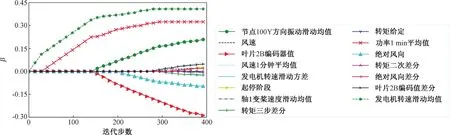
图3 LARS回归系数与迭代步数关系图Fig.3 The relationship between LARS regression coefficient and the number of iteration steps

选择LARS回归系数不为0的参数,即选择节点100Y方向振动滑动均值、风速、叶片2B编码器值、风速1分钟平均值、发电机转速滑动方差、起停阶段、轴1变桨速度滑动均值、转矩三步差分、转矩给定、功率1 min平均值、绝对风向、转矩二次差分、绝对风向差分、叶片2B编码值差分、发电机转速滑动均值作为模型的输入特征,由表1可以看出,选择这些参数与节点100X方向振动滑动均值的灰色关联度系数均大于0.5,本文还添加输出参量的前一个时刻值作为模型的输入参数[16]。

3 模型与实例分析

3.1 塔架振动状态监测模型

基于LSTM的塔架振动状态监测流程图如图4所示。

选取风电场26号机组数据建立塔架振动状态监测模型,使用1月～3月的数据作为LSTM模型的训练集,选取5月和6月的数据作为模型的测试集。建立LSTM模型时,采用三层LSTM网络相连接,并在网络后连接两层全连接层,根据SCADA的数据的输入量和输出量对网络参数进行设置。LSTM两层神经元的个数分别为60、55、40,全连接层的神经元个数分别为40,1。输入数据的时间步数timesteps设置为2,选择Adma作为模型的优化器,设置学习率为0.001,batch_size为400,epochs为150,选择均方误差函数来检验预测值和真实值之间的偏差。

为与提出的模型进行对比,本文还建立了BP网络模型和极限梯度提升(XGBoost)网络模型,使用同样的训练集分别对BP网络和XGBoost网络进行训练,建立塔架振动预测模型,并对相同的测试集进行预测。其中BP网络层数设为3层,神经元个数分别设为60、55、40,激活函数采用sigmoid函数,优化算法采用RMSprop,使用均方误差计算训练集和测试集的损失值,batch_size为1 000,epochs为 300。

为更加准确地评估模型的预测精度,使用可以体现模型预测值与真实值残差大小的平方和误差、均方误差和平均绝对误差作为模型的评价指标,计算结果如表2所示。

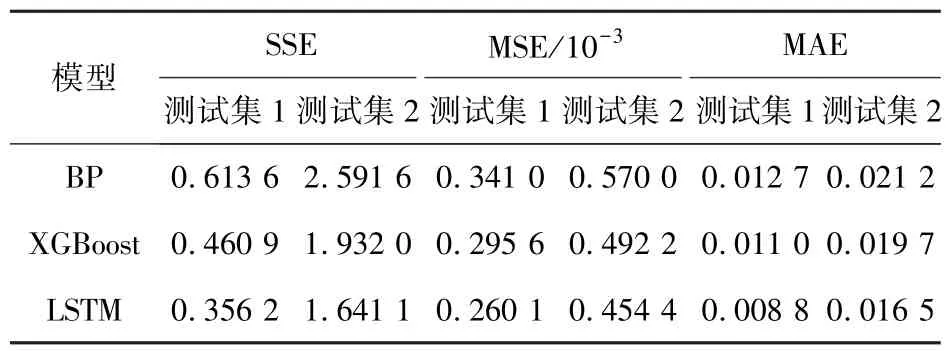
表2 不同模型精度评价指标Tab.2 Accuracy evaluation indexes of different models

由表2得出的结果可知,LSTM模型的2个测试集的3个评价指标SSE、MSE、MAE的值均小于XGBoost模型和 BP网络模型。针对测试集1,LSTM网络、XGBoost算法、BP网络建立的塔架振动预测模型的预测误差依次增大,且 LSTM和XGBoost模型误差相差不大,即塔架振动量较低时LSTM和XGBoost模型预测精度较高;针对测试集2,3种预测模型的预测误差相差较大,且LSTM模型的预测误差表现为最小,即振动量较高时后两种方法预测效果不如LSTM网络。总体表现为LSTM模型预测效果优于XGBoost模型预测效果,XGBoost模型预测效果优于 BP网络模型预测效果。

通过上述3种模型对2个测试集的预测误差的比较可以得出,基于LSTM的塔架振动状态预测模型能较好地预测塔架振动状态变化趋势,该模型很好地学习了风力发电机组正常运行过程中各状态变量与塔架振动量之间的关系,为下一步塔架异常振动识别及监测提供了基础。

3.2 实例分析

3.2.1 实例分析1

为验证提出方法的有有效性,选取和上述26号机组同一风电场48号机组进行验证。其中选取7月15日～8月15日的数据作为训练集,选取8月20日～8月24日、8月26日～8月27日的数据分别作为两组测试集。由于训练集残差为随机变量,一般满足正态分布,将训练集残差的置信度设为99.9%,满足99.9%以上的残差数据在阈值限以内,经过计算得出残差下限为-0.089,残差上限为0.099,即塔架正常振动状态下的残差应满足[-0.089,0.099]。LSTM、XGBoost、BP 网络 3种模型对两个测试集的预测结果如图5所示,LSTM模型训练集预测值与实际值的残差分布直方图和两个测试集的残差分别如图6和图7所示。

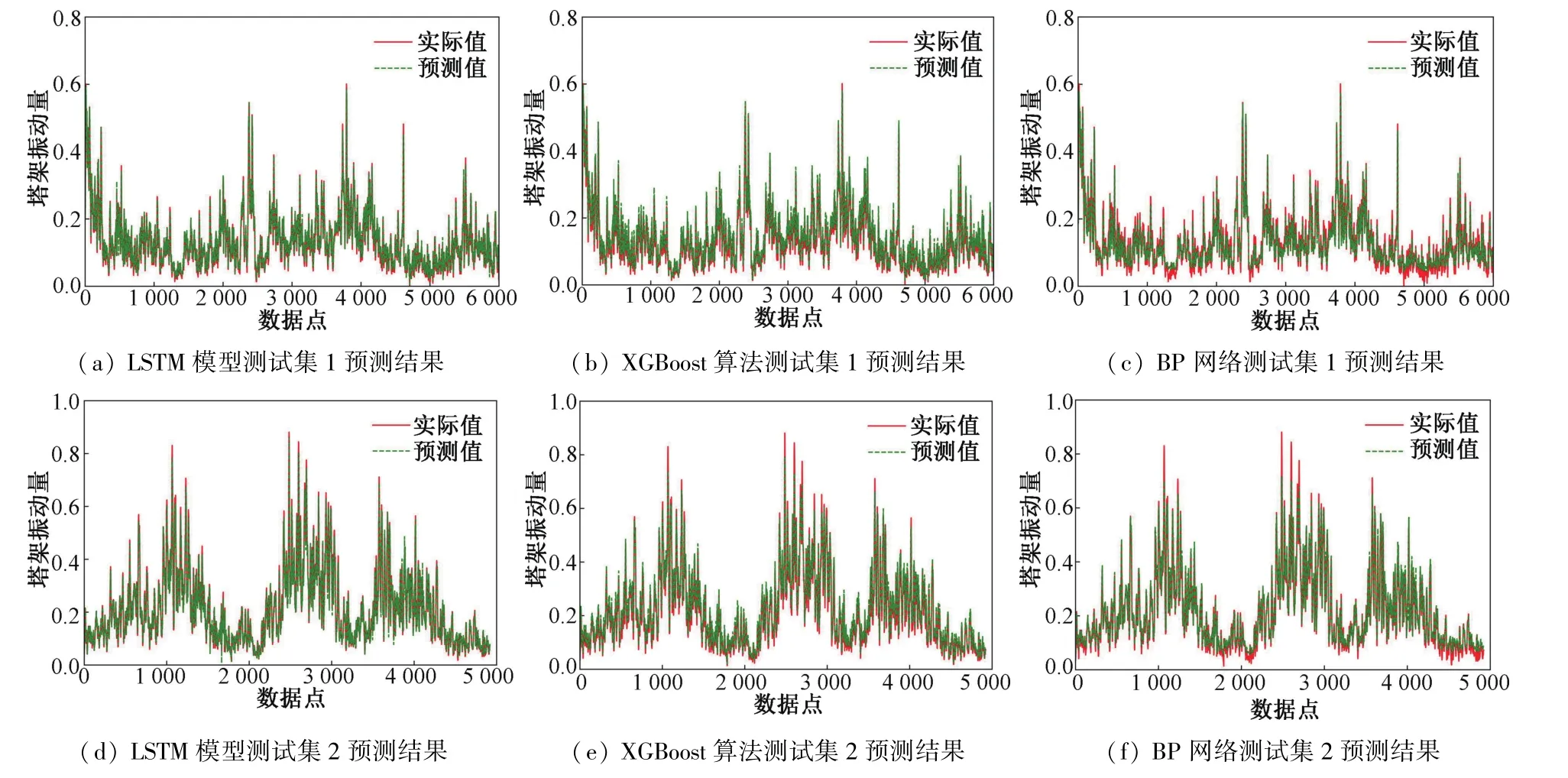
图5 48号机组3种模型预测结果图Fig.5 The prediction results of the three models of No.48 wind turbine

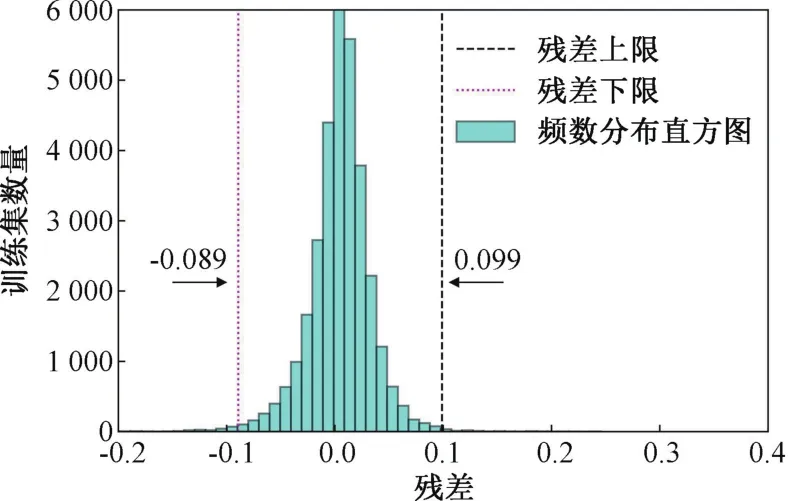
图6 48号风电机组训练集残差分布直方图Fig.6 Histogram of residual distribution of the training set of No.48 wind turbine

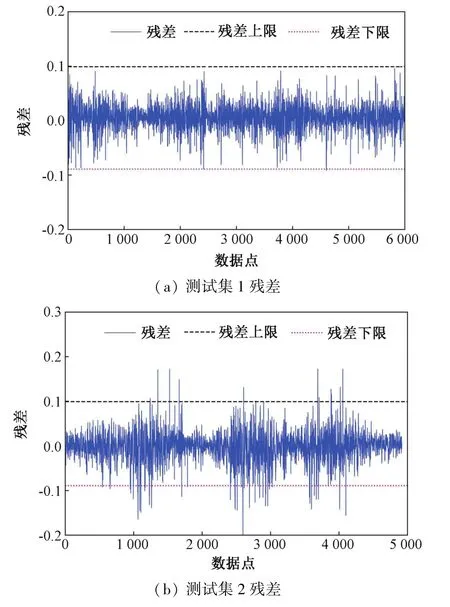
图7 48号风电机组预测结果和残差Fig.7 Forecast results and residuals of the No.48 wind turbine

由图7看出测试集1的预测值与真实值残差全部在上下阈值限之内。测试集2预测值与真实值的残差在1 000点初次越限,即8月26日出现第一次越限,之后出现多次越限,且越限值远超出阈值上下限,可以判定风电机组塔架出现异常振动。查询历史纪录,如表3机组编号为48的故障记录,该风电机组在8月31日,00:28:47时出现变流器故障报警,监测结果与历史记录一致,由于变流器故障,导致机组给定转矩迅速下降为0,发电机转速随之下降为0,导致机组紧急停机出现塔架振动异常。结果表明,该方法可提前5天对风电机组变流器故障发出警报,若在残差第一次超出阈值时对机组进行停机检查,可降低机组紧急停机给风电机组带来的损害。

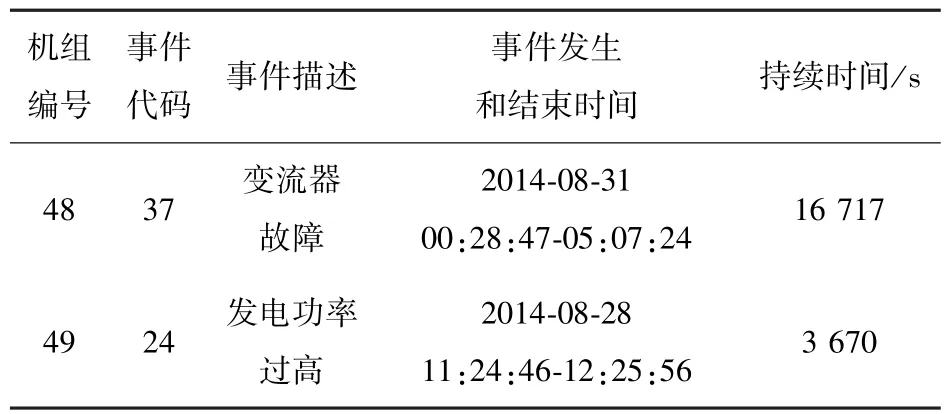
表3 故障记录表Tab.3 Table of fault record

3.2.2 实例分析2

选取与26号机组和48号机组同一风电场的49号机组对本文提出的模型进行验证和分析,将7月20至8月21日24900组样本作为模型的训练集,8月22日～8月24日、8月25～8月27日两组数据作为两组测试集,三种塔架振动预测模型对两组测试集的预测结果如图8所示。LSTM模型训练集残差频数分布直方图9所示,计算得到阈值范围为[-0.114,0.118],两个测试集的残差如图10所示。

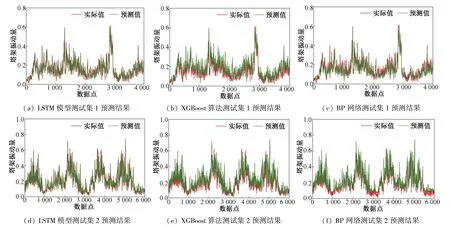
图8 49号机组三种模型预测结果图Fig.8 The prediction results of the three models of No.49 wind turbine

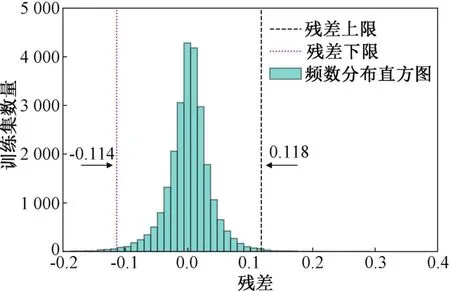
图9 49号风电机组训练集残差分布直方图Fig.9 The histogram of the residual distribution of the training set of the No.49 wind turbine

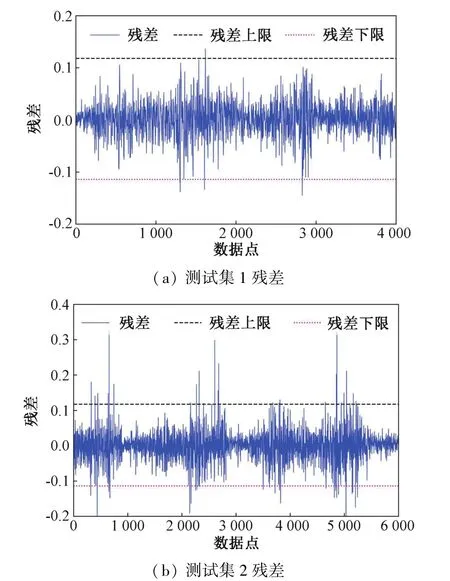
图10 49号风电机组预测结果和残差Fig.10 Forecast results and residuals of No.49 wind turbine

由图10可以看出,测试集1的残差基本都在阈值范围内,由于风向或风速波动较大导致残差偶尔超出阈值,在短时间内又恢复到阈值限以内。测试集2的残差在316点即8月25日出现第一次越限,在接下来的两天内出现多次越限,可以判定塔架为异常振动状态。查询历史纪录,该风电机组在8月28日11:24:46出现发电功率过高。在风电机组记录故障之前,为限制风机运行功率,变桨系统使桨距角在短时间内增大较大的角度,产生较大的气动载荷,激励塔架产生异常振动,故障记录如表4所示。结果表明,该方法可提前3天对风电机组发电功率过高发出警报,若在残差第一次超出阈值时对机组进行停机检查,可降低甚至避免机组因发电功率过高而导致的频繁紧急停机给风电机组带来进一步的损害。

4 结论

针对风电机组塔架振动问题,本文结合某风电场实际SCADA运行数据,对比分析了基于BP神经网络、XGboost算法和LSTM神经网络的塔架振动预测模型精度,使用风电场实际SCADA数据进行测试,结果表明,基于LSTM的塔架振动预测建模精度优于BP神经网络和XGboost算法。利用同一风电场两个机组的实际运行数据对所提方法进行验证,测试结果显示所提方法较SCADA系统能分别提早5天和3天对由变流器故障和发电功率过高导致的塔架异常振动做出预警,可以有效避免故障恶化引发的紧急停机对机组造成进一步的损害,降低了运维成本,提高了风电机组运行的可靠性。