基于超螺旋二阶滑模控制静止无功发生器的研究

魏毅立，尹晓航，刘志峰

（1.内蒙古自治区光热与风能发电重点实验室（内蒙古科技大学），内蒙古 包头 014010；2.内蒙古科技大学矿业与煤炭学院，内蒙古 包头 014010）

0 引言

三相电网不平衡运行会对电力系统和电力用户带来一系列的危害[1-4]。静止无功发生器（static var generator，SVG）广泛用于电力系统中解决三相不平衡的问题[5-6]。但是随着电网中电力电子设备的广泛应用，传统的SVG 控制方式已经难以满足用户对电网电能质量日趋提高的需要。

目前常用的SVG 电流检测方法为瞬时对称分量法[7-9]，但是由于移相算子的缘故，计算结果会因为引入延迟而带来误差。国内外学者对SVG 的控制系统提出了诸多控制方法，包括PI 控制，自适应控制，神经网络控制等，但是由于这些方法自身的局限性，比如自适应控制中对阶的不确定性十分敏感[10-12]，神经网络的实时性较差[13]等，尤其是SVG 非线性系统控制变量之间的强耦合性的原因，使得SVG 的控制变得困难[14]。

针对这种情况，本文提出一种基于改进瞬时对称分量法的电流检测方法，以达到对电能质量的实时提高。针对系统dq 轴上直流变量之间的相互耦合的原因，对电流环采用解耦控制，使其成为相互独立的直流分量。又由于在解耦控制器中，PI 控制器的参数难以确定，且其难以解决时变的复杂系统，故采用超螺旋（super-twisting）二阶滑模控制替代PI 控制，相较于PI 控制，其能满足系统对动态性能的要求且响应速度更快。再经过空间矢量调制策略（space vector pulse width modulation，SVPWM）调制产生触发功率开关器件的脉冲信号，从而实现动态无功补偿的目的。在Matlab 中对动态不平衡负载采用此方法进行仿真分析，并与采用传统的PI 控制的SVG 在无功补偿的表现上进行了对比，证明改进的控制补偿效果更为良好。

1 改进瞬时对称分量法

1.1 传统的对称分量法

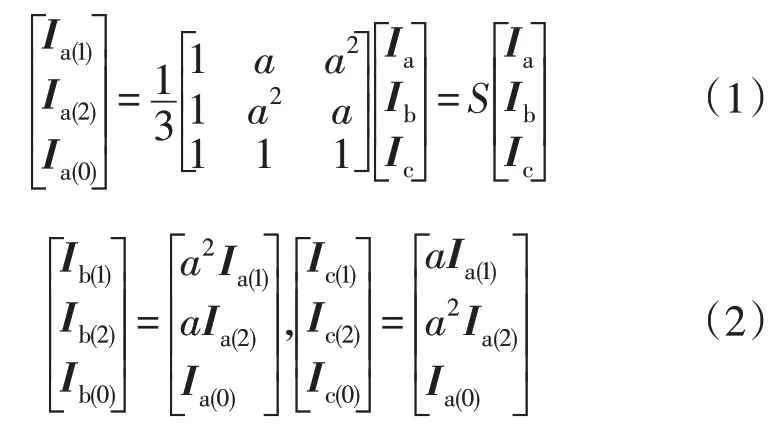
由式（1）、式（2）可知，对称分量法中的变量均为稳态值，因此传统对称分量法只适用于电力系统稳态分析。

1.2 改进瞬时对称分量法

针对传统对称分量法的不足，文献[15-16]提出了瞬时对称分量的概念，以适应动态和瞬时条件，并将其原理由电机理论中扩展至电力系统计算中。由于采用移相算子会引入延迟，因此提出改进瞬时对称分量法[17]。

设3 项不对称电流的瞬时值为

构造与其相对应旋转向量Ia、Ib、Ic，公式为

由式（4）可知，其虚部的系数，即为公式（3），因此由文献[18]可知实部的表达式

因此，电流值为

其中，Im 表示对复数取虚部。

1.3 广义dq变换

在αβ 坐标系中，有公式

式中，θ为同步旋转角。

将公式（5）进行αβ 变换，并使用公式（8）所示的同步旋转角θ，得到正序电流的广义dq 变换为

负序电流的广义dq 变换为

其所对应的逆变换为

1.4 电流检测原理图

基于瞬时对称分量法的正负序电流检测原理见图1。

图1 电流检测原理图Fig.1 Principle diagram of current detection

2 前馈解耦控制器的设计

2.1 SVG数学模型

SVG 本质上为并网型逆变器，其结构见图2。

图2 SVG结构图Fig.2 Structural diagram of SVG

三相静止坐标系下的数学模型为

式中：SL1、SL2、SL3为三相桥开关信号函数；USL1、USL2、USL3为电网电压；UL1、UL2、UL3为SVG 输出电压。

将公式（9）转换至dq 坐标系，公式为

其中，Sd、Sq分别为开关信号函数。

2.2 前馈解耦控制器的设计

由公式（10）可得公式为

式中：e为调制量；ed=Sd·udc；eq=Sq·udc；为状态变量，在控制中的作用为控制器。

从上式可以看出，ed中含有q轴分量，eq中含有d轴分量，ed、eq两方程相互耦合。根据文献[19]，电流环控制采用前馈解耦控制，控制结构见图3。

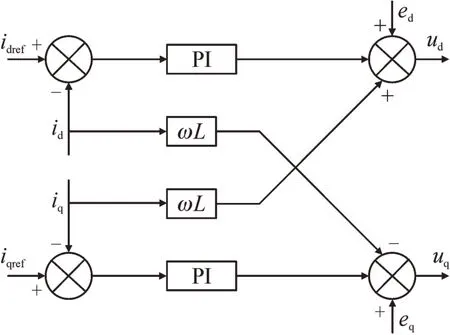
图3 前馈解耦控制Fig.3 Feedforward decoupling control

3 滑模控制

在解耦控制器中，PI 控制器的参数难以确定，且在负载突变时，PI 控制器不能满足系统对稳态性能和动态性能的要求。故采用滑膜控制替代PI 控制，相较于PI 控制，其能满足系统对稳态性能和动态性能的要求且响应速度更快。

3.1 滑模面的选取

由SVG 单相数学模型可知

令x=iL，由公式可得系统的非线性函数为

定义跟踪误差

式中：iL为参考电流指令；ireal为实际输出的电流。

SVG 电流控制环节的主要任务是实时准确地检测出电流，所以选取滑模面为

3.2 控制律

传统的滑膜控制虽然具有较强的动态性能，但其在本质上是一种非连续的控制方式，由于控制律离散性存在抖振问题，严重影响控制精度。超螺旋二阶滑膜控制算法通过将离散控制律转移到高阶，使控制量在时间上连续，能够有效的抑制抖振[20-21]。超螺旋二阶滑膜控制算法采用两部分组成，一是滑模面上的一个连续函数，设为u1，二是滑模面在时间上的积分，设为u2，公式为

由上式可以看出不连续的高频切换量αsign（s）不再直接影响控制律u，而是以时间积分的形式出现在超螺旋二阶滑模控制律中，从而获得连续的控制信号，因此可以消除传统滑模控制中的抖振缺陷。

为保证超螺旋二阶滑模控制在有限时间内收敛，需满足0 ＜ρ≤0.5[22]，此处ρ取值为0.5。

由公式（12）可知，超螺旋控制算法只需要知道滑膜变量s即可，基于以上信息，得到其控制律为

3.3 系统的稳定性分析

在控制原理中，为了分析系统的稳定性，通常采用Lyapunov 函数进行判断，为证明系统满足滑模控制的可达性条件ss＜0，构造正定函数，其中s即为公式（11）所选取的滑模面

对其两端求导可得到

当s＞0 时，SL=1，为使s＜0，需使uSL+RiL＜udc。因为补偿电流是直流侧的电容电压与电网电压的差值作用在连接电感上产生的，所以一般情况下，直流侧电容电压udc远大于电网电压uSL，其幅值约为电网电压的2～3 倍[23]，所以满足条件；当s＜0 时，SL=0，此时s＞0。所以超螺旋二阶滑模控制算法在有限时间内时收敛的，满足就滑模控制及可达性，系统稳定。

3.4 SVG双闭环控制系统框图

SVG 电压外环控制采用PI 控制，由文献[24-26]可知电压采用750 V 直流电压源，控制框见图4。

图4 SVG控制框图Fig.4 SVG control block diagram

由图4 可以看出，用超螺旋二阶滑模控制（sliding mode control，SMC）替代前馈解耦控制中的PI 控制。经电流环前馈解耦控制及超螺旋二阶滑模控制后产生的电压参考值，经dq-αβ变换，再经过空间矢量调制（SVPWM）产生脉冲作用在桥式电路上，进而来控制IGBT。

4 仿真分析

为了验证本文所提出的基于超螺旋二阶滑模控制静止无功发生器的不平衡负载补偿效果，在Matlab中搭建SVG 的系统仿真模型。设系统的3 项不平衡负载为动态负载，动态负载的仿真模型见图5。

图5 动态三相不平衡负载仿真模型Fig.5 Simulation model of dynamic three-phase unbalanced load

其电流波形见图6。

图6 动态三相不平衡负载电流波形Fig.6 Waveform of dynamic three-phase unbalanced load current

SVG 补偿前后电压电流波形见图7。

图7 SVG补偿前后三相电压电流波形Fig.7 Three-phase voltage and current waveform before and after SVG compensation

由图7 可以看出，本文所提出的基于超螺旋二阶滑模控制静止无功发生器对不平衡负载具有较好的补偿效果，补偿过后三相电压及三相电流趋于平衡，三相电压电流趋于同相位。

下面分别对本文所提出的SVG 系统的电流检测部分和无功补偿部分分别进行对比测试。

4.1 电流检测

为验证在SVG 中改进瞬时对称分量法对于电流实时检测的效果，将使用改进瞬时对称分量法的SVG 与使用ip-iq检测方法的SVG 分别在Matlab 中进行仿真，设定SVG 在0.3 s 之后接入系统中。对于二者在SVG 补偿前后相应快慢及电压电流波形相位差方面进行对比，见图8、图9。

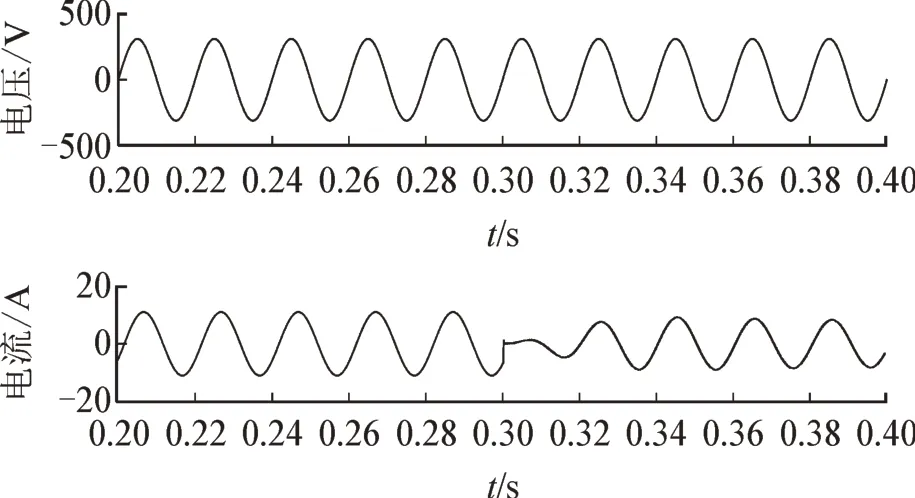
图8 瞬时对称分量法SVG接入前后电压电流波形Fig.8 Current and voltage voltage waveform before and after SVG access by instantaneous symmetric component method

图9 ip-iq 法SVG接入前后电流电压波形Fig.9 Current and voltage waveform before and after of SVGaccess by ip-iq method

SVG 的控制部分采用跟踪型脉冲宽度调制技术（pulse width modulation，PWM）电流控制方式中的三角载电流波控制方式，开关频率稳定，安全性能较好。SVG 直流侧电压采用PI 控制，直流侧电压取值750 V，远大于交流测电压峰值。设系统的3 项不平衡负荷为Ra=15 Ω，La=15 mH；Rb=20 Ω，Lb=20 mH；Rc=25 Ω，Lc=25 mH。仿真时间1.5 s。

以A 相电压和电流为例，由图8 图9 可知，SVG进行补偿前，电压电路存在相位差，采用改进瞬时对称分量法的SVG 与采用ip-iq检测方法的SVG 在接入0.045 s 之后电流电压相位相同。采用改进瞬时对称分量法的电流检测方法的SVG 可以快速地消除电压电流相位差。

基于改进瞬时对称分量法的静止无功发生器的电流检测方法无需锁相环和三角函数计算，使得计算过程易于实现，由Simulink 仿真结果表明，与采用ip-iq检测方法的SVG 相比，前者可以快速地进行电流补偿。

4.2 无功补偿

为验证基于超螺旋二阶滑模控制SVG 的无功补偿的效果，将其与采用传统PI 控制的SVG 分别在Matlab 中进行仿真，设定SVG 在0.3 s 之后接入系统中。对于二者在SVG 补偿后三相电流不平衡度、三相电流有效值之差、有功及无功功率波形、功率因数这几个方面进行对比。每一对比项的第1 张图为采用超螺旋二阶滑模控制SVG 的结果图，第2 张图为采用传统PI 控制的SVG 的结果图。

SVG 的电流检测部分采用改进瞬时对称分量法的电流检测方式，SVG 直流侧电压采用PI 控制，直流侧电压取值750 V。

4.2.1 SVG 补偿后电流不平衡度

采用超螺旋二阶滑模控制的SVG 在处理动态三相不平衡负载时的电流不平衡度约为0.3%，满足要求且远好于采用PI 控制的方式，见图10、图11。

图10 超螺旋二阶滑模控制SVG补偿后电流不平衡度Fig.10 Current unbalance after SVG compensation under super-spiral second-order sliding mode control

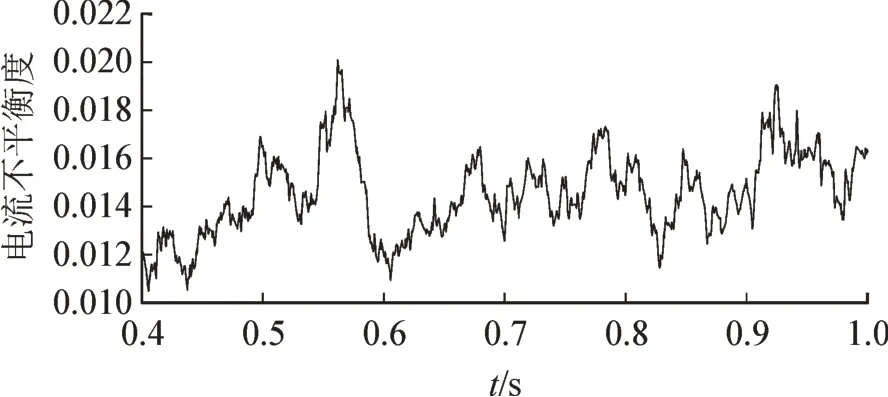
图11 PI控制SVG补偿后电流不平衡度Fig.11 Current imbalance after SVG compensation of PI control

4.2.2 SVG 补偿前后三相电流有效值之差

采用超螺旋二阶滑模控制的SVG 补偿前后三相电流有效值之差更小，三相电流更加趋于对称，见图12、图13。

图12 超螺旋二阶滑模控制SVG补偿前后三相电流有效值的差值Fig.12 Difference of effective values of three-phase current before and after SVG compensation under superhelical second order sliding mode control

图13 PI控制SVG补偿前后三相电流有效值的差值Fig.13 Difference of effective values of three phase current before and after SVG compensation of PI control

4.2.3 SVG 补偿前后有功及无功功率波形

由图14、图15 可以看出，相比于采用传统PI控制的SVG，采用超螺旋二阶滑模控制的SVG 补偿之后的有功功率无功功率更加趋于稳定。

图14 超螺旋二阶滑模控制SVG补偿前后有功及无功功率波形Fig.14 Active and reactive power waveform before and after SVG compensation under super-spiral second-order sliding mode control

图15 PI控制SVG补偿前后有功功率以及无功功率波形图Fig.15 Active and reactive power waveform before and after PI control SVG compensation

5 结语

本文提出一种新的SVG 电流检测方法以及基于超螺旋二阶滑模控制SVG 的控制方法。理论分析表明，基于改进瞬时对称分量法的静止无功发生器能够实时准确快速地进行电流检测。采用电流环解耦控制解决了dq 轴上直流变量之间耦合的缺陷；在静止无功发生器采用超螺旋二阶滑模控制能够完美替代PI 控制器。

基于理论推导，在Matlab 中分别对SVG 中改进瞬时对称分量法在电流实时检测中的效果以及采用超螺旋二阶滑模控制SVG 的无功补偿效果进行仿真分析。仿真结果表明，采用改进瞬时对称分量法的电流检测在SVG 与采用ip-iq检测方法的SVG 相比，前者在SVG 补偿前后相应快慢及电压电流波形相位差方面，与传统的瞬时对称分量法相比，更适用于无功补偿。基于改进瞬时对称分量法的超螺旋二阶滑模控制SVG 与采用传统PI 控制的SVG 相比，前者补偿过后电流不平衡度更好；三相电流更加趋于对称；有功及无功功率可以更加快速地趋于稳定；功率因数更低，与传统的PI 控制相比，更适用于无功补偿。